헤비사이드 스텝 함수

헤비사이드 스텝
헤비사이드 스텝
	하프-최대 규약을 사용하는 헤비사이드 스텝 함수
일반 정보
일반적인 정의
적용 분야	연산 미적분

Heaviside 스텝 함수 또는 단위 스텝 함수는 보통 H 또는 $δ$ ( $단$ , 때때로 $u$ , 1 $또는$ δ)로 나타나는 스텝 함수이며, 음의 인수에 대해서는 값이 0이고 양의 ^[1]인수에 대해서는 값이 0입니다.스텝 함수의 일반적인 클래스의 예이며, 이 모든 것은 이 함수의 변환의 선형 조합으로 나타낼 수 있습니다.

이 함수는 원래 미분방정식 해법을 위한 연산 미적분학에서 개발되었으며, 여기서 지정된 시간에 켜지고 무한히 켜진 상태를 유지하는 신호를 나타냅니다.전신통신 분석의 도구로 연산 미적분을 개발한 올리버 헤비사이드는 함수를 1로 $표현$ 했다.

헤비사이드 함수는 다음과 같이 정의할 수 있습니다.

부분 함수: $H(x):=param {case}1,&x>0\0,&x\leq 0\end{cases}$
지시 기능: $H(x):=\mathbf {1} _{x>0$
램프 기능의 파생 모델: $H(x):=paramfrac {d}{max}\max\{x,0\}\param{}x\neq 0$

디랙 델타 함수는 헤비사이드 함수의 파생 함수입니다.

\displaystyle \display (x) = flac {d} {dx}H(x)}

따라서 헤비사이드 함수는 디랙 델타 함수의 적분이라고 볼 수 있습니다.이것은 때때로 다음과 같이 쓰여진다.

H(x):=\int _{-\infty }^{x}\syslogs(s),ds

비록 이 확장이 x = $0$ 에 $대해$ 유지되지 않을 수도 있지만, 어떤 형식주의를 사용하여 $θ$ 를 포함하는 적분에 의미를 부여하느냐에 따라 의미가 달라진다.이 맥락에서 헤비사이드 함수는 거의 확실히 0인 랜덤 변수의 누적 분포 함수입니다(상수 랜덤 변수 참조).

연산 미적분학에서는 H가 주로 분포로 사용되기 $때문$ 에 H(0 $)$ 에 $사용$ 되는 값에 따라 유용한 답이 달라지는 경우가 거의 없다.그러나, 선택은 기능 분석과 게임 이론에서 몇 가지 중요한 결과를 가져올 수 있으며, 여기서 더 일반적인 형태의 연속성이 고려된다.일반적인 선택지는 다음과 같습니다.

헤비사이드 스텝 함수에 대한 근사치는 생화학 및 신경과학에서 사용되며, 스텝 함수의 로지스틱 근사치(힐 및 마이클리스-멘텐 방정식 등)를 사용하여 화학 신호에 대한 이항 셀 스위치를 근사할 수 있다.

분석적 근사치

({displaystyle {tfrac {1}{2}}+{\tfrac {1}{2}}\tanh(kx)=black {1}{1+e^{-2kx}}})

단계 함수에 k

\to 06

으로 접근합니다.

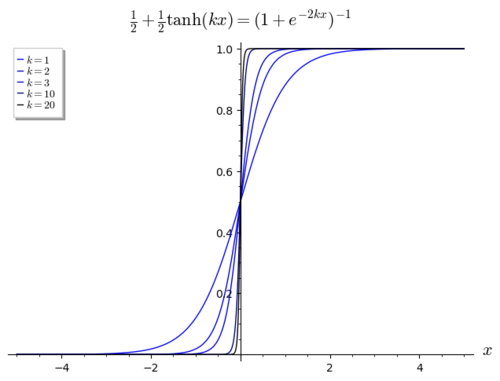
단계 함수에 대한 원활한 근사치를 위해 로지스틱 함수를 사용할 수 있습니다.

({displaystyle H(x)\약 {tfrac {1}{2}}+{\tfrac {1}{tfrac {2}}\tanh kx=black {1}{1+e^{-2kx}}}},

여기서 $k$ 가 클수록 x = $0$ 에서 더 날카로운 전이에 해당합니다.만약 우리가)H(0)을.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac.num,.mw-parser-output.sfrac .den{디스플레이:블록, line-height:1em, 마진:00.1em}.mw-parser-output.sfrac .den{border-top:1px.뚜껑}.mw-parser-output .sr-only{국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}1/2, 평등이 제한치에:보유하고 있다.

{\displaystyle H(x)=\lim _{k\to\infty}{\tfrac {1}{2}}=\lim _{k\to\infty}{\frac {1+e^{-2k}}}}.

스텝 ^[2]함수에는 그 밖에도 부드럽고 해석적인 근사치가 많이 있습니다.그 중에는 다음과 같은 것이 있습니다.

{begin{aligned}H(x)&=lim _{k\to\infty}\leftfrac {1}{\tfrac {2}+{\tfrac {1}+{\tfrc}+{\tfrc}\h(x}\lim _{k\infty }\infright}\fright}}

이러한 한계는 점으로 그리고 분포의 의미로 고정됩니다.단, 일반적으로 포인트 단위의 컨버전스가 분포의 컨버전스를 의미할 필요는 없으며, 그 반대의 경우 분포의 컨버전스가 포인트 단위의 컨버전스를 의미할 필요는 없습니다.(단, 점별 수렴 수열의 모든 멤버가 어떤 "나이스" 함수에 의해 균일하게 한정되어 있는 경우, 수렴은 분포의 의미에서도 유지됩니다.

일반적으로 분산을 제어하는 모수가 있는 연속 확률 분포의 누적 분포 함수는 분산이 0에 가까워지면 한계에서 근사치로 작용할 수 있습니다.예를 들어, 위의 세 가지 근사치는 각각 로지스틱 분포, 코시 분포 및 정규 분포의 누적 분포 함수입니다.

적분 표현

종종 Heaviside 스텝 함수의 적분 표현이 유용합니다.

{\displaystyle {\begin{aligned}H(x)&=lim _{\varepsilon\to 0^{2\pi i}}-int _{-\infty}^{\infty }{\frac {1}{\infty +i\varepsilon}}_e^{-ix\lim}\d}\lim =\d\lim\lim\d

여기서 단계 함수가 실재하고 따라서 그 자체의 복소 공역이라는 점을 고려할 때 두 번째 표현은 첫 번째 표현에서 추론하기 쉽다.

제로 인수

H는 보통 적분에 사용되며, 단일 지점의 함수의 값은 적분에 영향을 미치지 않기 $때문$ 에 H $(0)$ 중 어떤 $특정$ 값을 선택하는지는 거의 중요하지 않다.실제로 H를 L의 $분포 \infty$ 또는 요소(L $공간$ 참조^p)로 간주할 때, 이러한 개체는 거의 모든 곳에서 정의되기 때문에 0의 값을 말하는 것조차 의미가 없습니다.(위의 예와 같이) 분석적 근사치를 사용하는 경우, 종종 0에서 관련 한계치가 되는 모든 것이 사용된다.

특정 값을 선택하는 이유는 다양합니다.

그래프가 회전 $대칭$ 을 가지기 때문에 H(0)= 1 $/ 2$ 가 자주 사용됩니다. 바꿔 말하면 $H$ - $1 / 2$ 는 홀수 함수입니다.이 경우 기호 함수와의 관계는 $모든$ x에 대해 다음과 같습니다. $({displaystyle H(x)=tfrac {1}{2}}) (1+\operatorname {sgn} x).}$
$H (0)$ = $1$ 은 H가 오른쪽 연속이어야 할 때 $사용$ 됩니다.예를 들어, Lebegue-Stieltjes 통합에서 통합된 함수와 같이, 누적 분포 함수는 대개 오른쪽 연속 함수로 간주됩니다.이 $경우$ H는 닫힌 반무한 간격의 지시 함수입니다. $H(x)=\mathbf {1}_{[0,\infty}}(x).$ 대응하는 확률 분포는 퇴화 분포입니다.
$H (0)$ = $0$ 은 H가 왼쪽 연속이어야 할 때 $사용$ 됩니다.이 $경우$ H는 열린 반무한 간격의 표시 함수입니다. $H(x)=\mathbf {1}_{(0,\infty)}(x).$
최적화 및 게임 이론의 함수 분석 컨텍스트에서, 제한 함수의 연속성을 보존하고 특정 솔루션의 존재를 보장하기 위해 헤비사이드 함수를 집합값 함수로 정의하는 것이 종종 유용하다.이러한 경우, 헤비사이드 함수는 가능한 솔루션의 전체 $구간$ 인H( $0)$ = [ $0,1]$ 을 반환합니다.

이산형

$단위$ 단계의 대체 형태는 함수 H : δ→ $δ$ (즉, 이산 $변수$ n을 받아들임)로 정의되며, 다음과 같다.

H[n]=begin{cases}0,&n<0,\1,&n\geq 0,\end{cases

또는 절반 최대 ^[3]표기법을 사용합니다.

H[n]=begin{cases}0,&n<0,\{\tfrac {1}{2}},&n=0,\1,&n>0,\end{cases}}

$여기$ 서 n은 정수입니다.n이 정수일 $경우$ $n$ < $0$ 은 n - $-1$ 을 의미하고 $n$ > $0$ 은 함수가 n = $1$ 에서 통일됨을 의미해야 합니다.따라서 "스텝 함수"는 $[-1, 1]$ 의 영역에 걸쳐 램프와 같은 동작을 나타내며, 반최대 표기법을 사용하여 스텝 함수가 될 수 없다.

연속적인 경우와 달리 H $[0]$ 의 정의는 중요하다.

이산 시간 단위 임펄스는 이산 시간 단계의 첫 번째 차이입니다.

\displaystyle \display[n]=H[n]-H[n-1]}

이 함수는 크로네커 델타의 누적 합계입니다.

H[n]=\sum _{k=-\infty}^{n}\display [k]

어디에

(\displaystyle \displaystyle [k]=\displays _{k,0})

는 이산 단위 임펄스 함수입니다.

반파생파생파생파생파생파생파생파생.

램프 함수는 헤비사이드 스텝 함수의 역도함수입니다.

\displaystyle \int _{-\infty}^{x}H(\xi ), d\xi =xH(x)=\max\{0,x\},}

헤비사이드 스텝 함수의 분포 도함수는 Dirac 델타 함수입니다.

(\displaystyle\frac {dH(x)}{dx}=\delta(x)),}

푸리에 변환

헤비사이드 스텝 함수의 푸리에 변환은 분포입니다.푸리에 변환의 정의를 위해 하나의 상수 선택 사용

{H}=\lim _{N\to\infty}\int _{-N}^{N}{-2\pi ix}H(x),dx=scfrac {1}{2}\left(\display(s)-{\frac {i}{pi}}}\oper fronthorn {p}{p}{p}{p}{p}{p}.

$여기$ 서 p $. v$ .1 $/ s$ 는 테스트 함수 $θ$ 를 Cauchy의 주요 값인 $\textstyle \int _{-\infty }^{\infty }{\frac {\varphi (s)}{s}}\,ds$ θ - $\textstyle \int _{-\infty }^{\infty }{\frac {\varphi (s)}{s}}\,ds$ $\textstyle \int _{-\infty }^{\infty }{\frac {\varphi (s)}{s}}\,ds$ （ $\textstyle \int _{-\infty }^{\infty }{\frac {\varphi (s)}{s}}\,ds$ s ) $\textstyle \int _{-\infty }^{\infty }{\frac {\varphi (s)}{s}}\,ds$ $\textstyle \int _{-\infty }^{\infty }{\frac {\varphi (s)}{s}}\,ds$ s $\textstyle \int _{-\infty }^{\infty }{\frac {\varphi (s)}{s}}\,ds$ \ $displaystyle$ \ $int$ _ { - \ $infty }^{$ \ $infty }{$ \ $frac$ \ $varphi$ ( s ) { $s$ } { s}{ \ infty } { \ $\textstyle \int _{-\infty }^{\infty }{\frac {\varphi (s)}{s}}\,ds$ ds $\textstyle \int _{-\infty }^{\infty }{\frac {\varphi (s)}{s}}\,ds$ } {\ ds}에 나타나는 한계치도 $적분포함수$ 입니다.

일방 라플라스 변환

헤비사이드 스텝 함수의 라플라스 변환은 meromaphic 함수입니다.일방적인 Laplace 변환을 사용하면 다음과 같은 이점이 있습니다.

{\displaystyle {\hat {H}}&=\lim _{N\to\infty}\int _{0}^{N}e^{-sx}H(x),dx\&=\lim _{N\to\infty}\int _0^{x}e={-x}&lim

쌍방향 변환을 사용하면 적분을 두 부분으로 분할할 수 있으며 결과는 동일합니다.

기타 표현

헤비사이드 스텝 함수는 다음과 같이 하이퍼 함수로 표현될 수 있습니다.

\displaystyle H(x)=\left(1-{\frac {1}{2\pi i}}\log z, -{\frac {1}{2\pi i}}\log z\right).}

여기

서

log

z는

z

의 복소수 로그의 주요 값입니다.

또한 절대값 함수의 관점에서 x $0$ 0에 $대해$ 다음과 같이 나타낼 수 있다.

H(x)=syslogfrac {x+x}{2x}},

「」를 참조해 주세요.

레퍼런스

^ Zhang, Weihong; Zhou, Ying (2021). "Level-set functions and parametric functions". The Feature-Driven Method for Structural Optimization. Elsevier. pp. 9–46. doi:10.1016/b978-0-12-821330-8.00002-x. Heaviside function, also called the Heaviside step function, is a discontinuous function. As illustrated in Fig. 2.13, it values zero for negative input and one for nonnegative input.
^ Weisstein, Eric W. "Heaviside Step Function". MathWorld.
^ Bracewell, Ronald Newbold (2000). The Fourier transform and its applications (3rd ed.). New York: McGraw-Hill. p. 61. ISBN 0-07-303938-1.

외부 링크

수학 함수 디지털 라이브러리, NIST, [1].
Berg, Ernst Julius (1936). "Unit function". Heaviside's Operational Calculus, as applied to Engineering and Physics. McGraw-Hill Education. p. 5.
Calvert, James B. (2002). "Heaviside, Laplace, and the Inversion Integral". University of Denver.
Davies, Brian (2002). "Heaviside step function". Integral Transforms and their Applications (3rd ed.). Springer. p. 28.
Duff, George F. D.; Naylor, D. (1966). "Heaviside unit function". Differential Equations of Applied Mathematics. John Wiley & Sons. p. 42.

[Zhang_Zhou_2021_pp._9–46-1] Zhang, Weihong; Zhou, Ying (2021). "Level-set functions and parametric functions". The Feature-Driven Method for Structural Optimization. Elsevier. pp. 9–46. doi:10.1016/b978-0-12-821330-8.00002-x. Heaviside function, also called the Heaviside step function, is a discontinuous function. As illustrated in Fig. 2.13, it values zero for negative input and one for nonnegative input.

[2] Weisstein, Eric W. "Heaviside Step Function". MathWorld.

[3] Bracewell, Ronald Newbold (2000). The Fourier transform and its applications (3rd ed.). New York: McGraw-Hill. p. 61. ISBN 0-07-303938-1.

[1]

[2]

[3]

Search

헤비사이드 스텝 함수

네임스페이스

더

목차

분석적 근사치

적분 표현

제로 인수

이산형

반파생파생파생파생파생파생파생파생.

푸리에 변환

일방 라플라스 변환

기타 표현

「」를 참조해 주세요.

레퍼런스

외부 링크

Search

헤비사이드 스텝 함수

분석적 근사치

적분 표현

제로 인수

이산형

반파생파생파생파생파생파생파생파생.

푸리에 변환

일방 라플라스 변환

기타 표현

「 」를 참조해 주세요.

레퍼런스

외부 링크

「」를 참조해 주세요.