PERT 분포

PERT

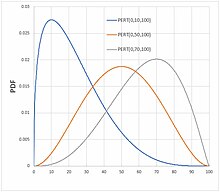확률밀도함수 PERT 확률 분포의 밀도 곡선 예제
누적분포함수 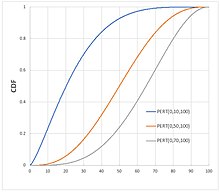PERT 확률 분포의 누적 분포 곡선 예제
매개변수	$(displaystyle b)a\,}$ (진짜) $(\displaystyle c>b\,}$ (진짜)
지원	$[a,c]\,}$
PDF	${\displaystyle {\frac {(x-a)^{\alpha -1}(c-x)^{\beta -1}}{\mathrm {B} (\alpha ,\beta )(c-a)^{\alpha +\beta -1}}}}$ where ${\displaystyle \alpha ={\frac {4b+c-5a}{c-a}}=1+4{\frac {b-a}{c-a}}}$$$ ${\displaystyle \csi ={\frac {5c-a-4b}{c-a}=1+4{\frac {c-b}{c-a}}}}$
CDF	${\displaystyle I_{z}(\alpha ,\beta )}$ (정규화된 불완전한 베타 함수) $z{\displaystyle }$=${\displaystyle }$( ${\displaystyle x}$- ${\displaystyle a}$)${\displaystyle }$/${\displaystyle }$( ${\displaystyle c}$-${\displaystyle }$) ${\displaystyle$ z$=(x-a)/(c-a)}$
평균	${\displaystyle \operatorname {E} [X]={\frac {a+4b+c}{6}}}=\mu }$
중앙값	${\displaystyle I_{\frac {1}{1}:{1}^{[-1](\alpha ,\beta )(c-a)+a}$ ${\displaystyle \c-a){\frac {\frac {\fract -1/3}{\flac +\flash -2/3}={\frac {a+6b+c}{8}}}$
모드	$(\displaystyle b)$
분산	${\displaystyle \operatorname {var} [X]={\frac {(\mu -a)(c-\mu )}{7}}}$
왜도	${\displaystyle {\frac {2\,(\frac -\propert ){\sqrt {\buffer +\buffer +1}{\sqrt {\buffer \pair \}}}}}$
엑스트라 쿠르토시스	${\displaystyle {6[(\frac -\frac )^{2}(\filency +\filency +1)-\filency \filency (\filency +\filency +2)]}{\cHB \cHB(\cHB +\cHB +2)}(\cHB +\cHB +3)}}$

확률과 통계에서 PERT 분포는 변수가 취할 수 있는 최소 (a), 가장 가능성이 높은 (b) 및 최대 (c) 값으로 정의된 연속 확률 분포의 집합이다.4-모수 베타 분포의 변환이며, 기대값은 다음과 같은 추가 가정을 한다.

${\displaystyle \mu ={\frac {a+4b+c}{6}.}$

따라서 분포의 평균은 변수가 취할 수 있는 최소값, 가장 가능성 있는 값 및 최대값의 가중 평균으로 정의되며, 가중치는 가장 가능성이 높은 값에 4배가 적용된다.평균에 대한 이러한 가정은 프로그램 평가와 검토 기법을 사용하여 평가되는 프로젝트 일정의 결과에 대한 작업 기간의 불확실성의 영향을 추정하기 위해 1962년^[1] Clark에서 처음 제안되었다. 따라서 그 명칭은 다음과 같다.분포의 수학은 표준편차를 범위의 약 1/6로 만들고자 하는 저자들의 열망에서 비롯되었다.^[2][3]PERT 분포는 분포를 정의하는 세 가지 모수가 추정기에 직관적이기 때문에 주관적 추정에 의존하는 일부 수량의 값의 불확실성을 나타내기 위해 위험 분석에^[4] 널리 사용된다.PERT 배포는 대부분의 시뮬레이션 소프트웨어 도구에 포함되어 있다.null

삼각형 분포와의 비교

PERT 분포는 동일한 세 개의 모수를 갖는 삼각 분포를 사용하는 대안을^[5] 제공한다.PERT 분포는 삼각 분포보다 부드러운 형태를 가지고 있다.삼각형 분포는 세 모수의 평균과 같다.

${\displaystyle \mu ={\frac {a+b+c}{3}}}$

(PERT와는 달리) 일반적으로 가장 가능성이 높은 값보다 잘 알려져 있지 않고 따라서 신뢰성이 낮은 극단값을 동일하게 강조한다.또한 삼각형 분포는 주관적인 지식을 전형적으로 나타내는 부드러운 모양과 일치하지 않는 각형 형태를 가지고 있다.null

수정-PERT 분포

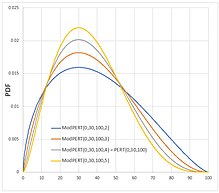
PERT 분포는 극단값, 특히 분포가 강하게 치우친 경우 가장 가능성이 높은 값에서 가장 멀리 떨어진 극단값에는 매우 작은 확률을 할당한다.^[6][7]수정된 PERT 분포는 분포의 꼬리 값에 얼마나 많은 확률을 할당하는지에 대한 더 많은 제어를 제공하기 위해 제안되었다.수정된-PERT는 평균의 결정에서 가장 가능성이 높은 값의 가중치를 제어하는$$ 네 $번째{\displaystyle }$ 매개 변수${\displaystyle }$parameter , ${\displaystyle \gamma$}을(를) 도입한다.

${\displaystyle \mu ={\frac {a+\propert b+c}{\property +2}}:}$

일반적으로 $2$에서${\displaystyle }$3.5 사이의$$값은 $display$ , {\$displaystyle$\gamma $,}$에 사용되며$$ 밀도 곡선을 평평하게 만드는 효과가 있다.거리$({\displaystyle b}$- ${\displaystyle a}$ )${\displaystyle }$,${\displaystyle (b-a),}$ 및$$${\displaystyle }$( ${\displaystyle c}$- ${\displaystyle b}$)${\displaystyle }$, ${\displaystyle (c-b)}$의 크기가 매우$$ 다른 편향된 분포에 유용하다.null

수정된 PERT 배포는 다음과 같은 몇 가지 시뮬레이션 패키지와 프로그래밍 언어로 구현되었다.

• ModelRisk^[9] – Excel에 대한 위험 분석 추가 기능.
• Primavera 리스크 분석 – 프로젝트 리스크 분석 시뮬레이션 도구
• Tamara – 프로젝트 리스크 분석 시뮬레이션 도구.
• Wolfram Mathematica^[11] – 수학 기호 연산 프로그램.
• R(프로그래밍 언어): mc2d 패키지.^[12]
• Python(프로그래밍 언어): perdist 패키지.^[13]

참조