래핑 지수 분포

래핑 지수

확률밀도함수 지원은 [0,2π]로 선택된다.
누적분포함수 지원은 [0,2π]로 선택된다.
매개변수	$\displaystyle \lambda >0}$
지원	$\displaystyle 0\leq \theta <2\pi }$
PDF	${\displaystyle {\frac {\buffda e^{-\buffda \theta }}{1-e^{-2\pi \pi \}}}}}}}}$
CDF	${\displaystyle {\frac {1-e^{-\boda \theta }}{1-e^{-2\pi \da }}}}}}}$
평균	${\displaystyle \arctan }$ ${\displaystyle }$(${\displaystyle 1}$/${\displaystyle \lambda }$ ) ${\displaystyle \arctan(1/\lambda )}(})$
분산	${\displaystyle 1}$ -${\displaystyle \lambda \frac{}{}}$ ${\displaystyle \frac{\sqrt{1\mathrm{}}}{}}$+ ${\displaystyle \frac{\sqrt{{}^{}}}{}}$ ${\displaystyle \frac{\sqrt{{2\mathrm{}}^{}}}{}}$ ${\$으)
엔트로피	${\displaystyle 1+\ln \left({\frac {\beta -1}{\lambda }}\right)-{\frac {\beta }{\beta -1}}\ln(\beta )}$ where ${\displaystyle \beta =e^{2\pi \lambda }}$ (differential)
CF	${\displaystyle {\frac {1}{1-in/\probda }}$

확률 이론과 방향 통계에서 래핑된 지수 분포는 단위 원을 둘러싼 지수 분포의 "래핑"에서 비롯되는 래핑된 확률 분포다.null

정의

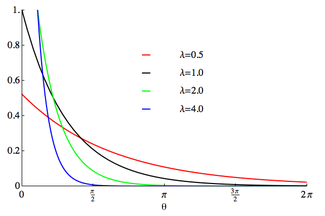
래핑된 지수 분포의 확률밀도함수는^[1]

$f_{\displaystyle f_{WE}(\theta ;\lambda )=\sum _{k=0}^{\inful }\lambda e^{-\lambda (\theta +2\pi k)}={\frac {\lambda \}}}{1-e^{2\pi }}}}}}}$

< ${\displaystyle 0\leq \theta <2\pi }$에 대해 여기서 >0 ${\displaystyle$\ \$da$ >$0}$은 포장되지 않은 분포의 속도 매개 변수다.이는 비율 매개변수가 λ인 지수 분포에서 관측값 X를 < $[\displaystyle 0\leq X<2\pi }$의 범위로 제한하여 얻은 잘린 분포와 동일하다

특성함수

래핑된 지수의 특성 함수는 정수 인수로 평가된 지수함수의 특성 함수에 불과하다.

${\displaystyle \varphi _{n}(\fracda )={\frac {1}{1-in/\froda }}}$

모든 실제 real과 m에 유효한 순환 변수 z=e의 ^{i (θ-m)} 관점에서 래핑된 지수 PDF에 대한 대체 식을 산출한다.

${\displaystyle {\buffered}f_{{WE}(z;\lambda )&={\frac {1}{2\pi }\sum _{n=-\inflt }{n=\inflt }{z^{-n}{1in/\lambda }\[10pt]&#{n}={\begin{cases}{\frac {\lambda }{\pi }}\,{\textrm {Im}}(\Phi (z,1,-i\lambda ))-{\frac {1}{2\pi }}&{\text{if }}z\neq 1\\[12pt]{\frac {\lambda }{1-e^{-2\pi \lambda }}}&{\text{if }}z=1\end{cases}}\end{aligned}}}$

여기서 $\phi {\displaystyle \mathrm{}}$(${\displaystyle }$) ${\displaystyle \Phi()}$은(는) Lerch 초월 함수다.null

순환모멘트

원형 변수 $z{\displaystyle }$= ${\displaystyle {}^{}}$ ${\displaystyle {\theta }^{}}$ ${\$의 관점에서$$, 래핑된 지수 분포의 원형 모멘트는 정수 인수로 평가되는 지수 분포의 특성 함수다.

$\displaystyle \langle z^{n}\angle =\int_{\\\\\\\\\\\\\\n_{\\\\\\\\\\\\\\\\}\\\\\{\\\\\\WE}(\theta ;\lambda )\,d\d\theta ={\frac {1}{1-in/\lambda }},}$

여기서 $\gamma {\displaystyle \mathrm{}}$ ${\$은(는) 길이 $2{\displaystyle \mathrm{}}$ $[\displaystyle 2\pi }$의 일부 구간이다$.$ 첫 번째 순간은 평균 결과물 또는 평균 결과 벡터라고도 알려진 z의 평균 값이다.

${\displaystyle \langle z\angle ={\frac {1}{1-i/\probda }}.}$

평균각은

$\displaystyle \langle \theta \rangle =\mathrm {Arg} \langle z\rangle =\arctan(1/\lambda ),}$

평균 결과물의 길이는

${\displaystyle R= \langle z\rangle ={\frac {\lambda }{\sqrt{1+\lambda ^{2}}}.}$

그 다음 분산이 1-R이다.null

특성화

래핑된 지수 분포는 $기대{\displaystyle \mathrm{}}$ E${\displaystyle (}$ ($$의 고정 값에 0 < 2π < 2 ${\displaystyle \pi }$ {\$displaystyle 0\leq$$\theta$<$2\$pi $}}$로 제한된 분포의 최대 엔트로피 $확률$ 분포이다$.$^[1]

참고 항목

• 포장배포
• 방향통계

참조