의미하다

이 기사의 리드 섹션이 너무 짧아서 요점을 적절하게 요약할 수 없을 수 있습니다. 기사의 모든 중요한 측면에 대한 접근 가능한 개요를 제공하기 위해 리드를 확장하는 것을 검토하십시오. (2021년 10월)

수학, 특히 통계학에는 몇 가지 종류의 평균이 있다.각 평균은 주어진 데이터 그룹을 요약하는 역할을 하며, 종종 주어진 데이터 세트의 전체 값(크기와 부호)을 더 잘 이해하기 위해 사용됩니다.

데이터 집합에서 "산술 평균"이라고도 하는 산술 평균은 유한한 숫자의 집합의 중심 경향을 나타내는 척도입니다. 구체적으로는 값의 합을 값의 수로 나눈 값입니다.숫자 x1, 미국의 산술 평균...., xn 일반적으로 고가 바를 사용하여,)¯{\displaystyle{\bar{)}}}.[노트 1]만약은 데이터 세트 관찰의 시리즈가 통계적 모집단에서 표본 추출에 의해 입수에 근거한 것이었다, 산술 평균. 표본 평균()¯{\displaystyle{\bar{x}}})에 표시됩니다. distinguish 기본 분포의 평균 또는 기대치로부터 모집단 평균$({displaystyle\mu}$ $또는$ ${\displaystyle {\mu }_{}}$x {\$displaystyle\mu_{x})$^{[note 2][1]}을 구합니다.

확률과 통계 이외에도, 기하학과 수학적 분석에는 다양한 평균 개념이 사용된다. 아래에 예가 제시되어 있다.

평균의 종류

피타고라스의 의미

산술평균(AM)

숫자 목록의 산술 평균(또는 단순히 평균)은 모든 숫자의 합을 숫자 수로 나눈 것입니다.${\displaystyle {}_{}}$로 샘플${\displaystyle {}_{}{x\mathrm{}}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$, ${\displaystyle {}_{}}$2, ${\displaystyle \dots ,}$ x $($$보통{\displaystyle \stackrel{}{}}$ x${\$ { $displaystyle$$$x _ {1} , $x$_ {2$}$ , \$ldots$, x$_$ { $n$} )의 평균은 샘플 값을 샘플 $내$의 항목 수로 나눈 값입니다.

${{displaystyle {x}}=subfrac {1}{n}\left(\sum _ {i=1}^{n} {x_{i}}\right)=subfrac {x_{1}+x_{2}+\cdots +x_{n}{n}}}}}}$

예를 들어 4, 36, 45, 50, 75의 5가지 값의 산술 평균은 다음과 같습니다.

${\displaystyle\frac{4+36+45+50+75}{5}} = flac {210} {5} = 42.}$

기하평균(GM)

기하 평균은 양수 집합에 유용한 평균으로, 합(산술 평균)이 아니라 곱(성장률)에 따라 해석됩니다.

${\displaystyle {x}=\left(\displaystyle _ {i=1}^{n}\right)^{\frac {1}{n}=\left(x_{1}x_{2}\cdots x_{n}\right)^{\frac {1}{n}}}$ ^[2]

예를 들어 4, 36, 45, 50, 75의 5가지 값의 기하 평균은 다음과 같습니다.

${\displaystyle(4\times 36\times 50\times 75)^{\frac {1}{5}=syslogrt[{5}}{24\;300\;000}=30.}$

고조파 평균(HM)

고조파 평균은 속도의 경우(즉, 시간 단위당 거리)와 같이 어떤 단위와 관련하여 정의된 숫자의 집합에 유용한 평균이다.

${\displaystyle {x}=n\left(\sum _{i=1}^{n}{\frac {1}{x_{i}}\right)^{-1}$

예를 들어, 4, 36, 45, 50, 75의 5가지 값의 조화 평균은

$({displaystyle {\tfrac {1}{4}}+{\tfrac {1}{36)}+{\tfrac {1}{45}}+{\tfrac {1}{75}}}=frac {5}{\;{\tfrac {1}{3}}}.}$

AM, GM 및 HM의 관계

AM, GM 및 HM은 다음과 같은 불평등을 충족합니다.

$\displaystyle \mathrm {AM} \geq \mathrm {GM} \geq \mathrm {HM} , }$

주어진 표본의 모든 요소가 동일한 경우 동등성이 유지됩니다.

통계적 위치

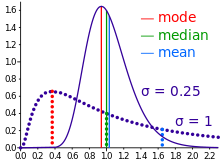
기술 통계량에서 평균은 중위수, 모드 또는 중간 범위와 혼동될 수 있습니다. 이 중 하나를 "평균"이라고 부를 수 있기 때문입니다.관측치 집합의 평균은 값의 산술 평균이지만 치우친 분포의 경우 평균이 중간값(중간값) 또는 가장 가능성이 높은 값(모드)과 반드시 같지는 않습니다.예를 들어, 평균 소득은 일반적으로 매우 큰 소득을 가진 소수의 사람들에 의해 위로 치우쳐져 있으므로, 대다수의 소득은 평균보다 낮다.반면 중위소득은 인구의 절반이 아래이고 절반이 위인 수준입니다.모드 소득은 가장 가능성이 높은 소득이며 소득이 낮은 더 많은 사람들을 선호한다.중위수와 모드는 종종 이러한 치우친 데이터에 대해 더 직관적인 측도이지만, 실제로 지수 분포와 포아송 분포를 포함하여 많은 치우친 분포가 평균으로 가장 잘 설명됩니다.

확률 분포의 평균

확률 분포의 평균은 해당 분포를 가진 랜덤 변수의 장기 산술 평균 값입니다.랜덤 변수가 X$(\displaystyle$ X$)$로 표시되는 경우 X$(\displaystyle$X$displaystyle$ E$(X))$의 예상값이라고도 합니다.이산 확률 분포의 경우 평균은${\displaystyle \delta }$ ${\displaystyle x}$ P${\displaystyle }$(${\displaystyle x}$) \$displaystyle \textstyle \sum$ xP$(x$로 지정되며, 여기서 합계는 랜덤 변수의 모든 가능한 값에 적용되며 $P{\displaystyle }$(${\displaystyle x}$) \$displaystyle$ P$(x)$는 확률 질량 함수입니다.연속분포의 경우 평균은${\displaystyle {}_{}^{}}$δ -${\displaystyle {\mathrm{}}_{}^{}}$δ${\displaystyle {}_{}^{}x}$ ${\displaystyle f}$ (${\displaystyle x}$ )${\displaystyle d}$ x x x ${\$ _${-\infty }^{\infty }xf(x),dx$^[4]입니다.$여기$서${\displaystyle }$f$(x)$는 확률밀도함수입니다.분포가 이산 분포도 연속 분포도 아닌 경우를 포함하여, 평균은 확률 측도에 대한 랜덤 변수의 르베그 적분입니다.평균이 존재하거나 유한할 필요는 없습니다. 일부 확률 분포의 경우 평균이 무한(+θ 또는 -θ)인 반면 다른 분포의 경우 평균이 정의되지 않습니다.

일반화 수단

검정력 평균

검정력 평균 또는 쾰더 평균이라고도 하는 일반화 평균은 2차, 산술, 기하학 및 조화 평균을 추상화한 것입니다.이는 n개의 양수_i 세트x에 대해 다음과 같이 정의된다.

${\displaystyle {x}(m)=\left\frac {1}{n}\sum _{i=1}^{n}x_{i}^{m}\right)^{\frac {1}{m}}}$ ^[2]

매개변수 m에 대해 다른 값을 선택하면 다음과 같은 유형의 평균을 얻을 수 있습니다.

${\displaystyle \lim _{m\to \infty }}$

$최대{\displaystyle {}_{}}$ $($ 스타일 $x_{i$})

${\displaystyle \lim _{m\to 2}}$

이차 평균

${\displaystyle \lim _{m\to 1}}$

산술 평균

${\displaystyle \lim _{m\to 0}}$

기하 평균

${\displaystyle \lim _{m\to -1}}$

조화 평균

${\displaystyle \lim _{m\to -\infty }}$

$최소{\displaystyle {}_{}}$ $($ 스타일 $x_{i$})

f-평균

이것은 일반화 f-평균으로서 더 일반화 될 수 있다.

$({displaystyle {x}=f^{-1}\leftfrac{n}\sum _{i=1}^{n}{f\left(x_{i}\right)}\right)}}$

그리고 다시 가역 f의 적절한 선택은 다음을 줄 것이다.

${\displaystyle f(x)=x}$	산술 평균,
${\displaystyle f(x)=paramfrac {1}{x}}$	조화 평균,
${\displaystyle f(x)=x^{m}}$	전력 평균,
${\displaystyle f(x)=\ln(x)}$	기하 평균

가중 산술 평균

가중 산술 평균(또는 가중 평균)은 동일한 모집단의 서로 다른 크기 표본의 평균 값을 결합하려는 경우 사용됩니다.

$({displaystyle {x}}=par frac {sum _ {i=1}^{n} {w_{i}}}}{\sum _ {i=1}^{n}w_{i}}}}.}$ ^[2]

$여기$서 x i${\$ （ { $displaystyle${ x _$${ i } }}} w w i $i$、 w i （ $displaystyle$ $w$_ {$i$$$} ）는 $샘플$$i$의 평균 및 크기입니다.다른 응용 프로그램에서는 각 값에 의한 평균에 대한 영향의 신뢰성에 대한 측정값을 나타냅니다.

절사 평균

때때로 숫자 집합에는 특이치(즉, 다른 값보다 훨씬 낮거나 훨씬 높은 데이터 값)가 포함될 수 있습니다.특이치는 아티팩트로 인해 발생하는 잘못된 데이터인 경우가 많습니다.이 경우 잘린 평균을 사용할 수 있습니다.여기에는 데이터의 일부(일반적으로 각 끝에서 동일한 양)를 폐기한 다음 나머지 데이터의 산술 평균을 취하는 작업이 포함됩니다.삭제된 값의 수는 총 값의 백분율로 표시됩니다.

사분위간 평균

사분위간 평균은 잘린 평균의 특정 예제입니다.이는 단순히 최소값과 최대값을 제거한 후의 산술 평균입니다.

${{displaystyle {x}}={bar frac {2}{n}}\;\sum _{i=bar frac {n}{4}}+1}^{\frac {3}{4}}n}\!\!x_{i}}$

값이 정렬되었다고 가정하면 특정 가중치 집합에 대한 가중 평균의 특정 예에 불과합니다.

함수의 평균

어떤 상황에서는 수학자들이 무한(또는 셀 수 없는) 값의 집합을 평균으로 계산할 수도 있습니다.이는 $함수{\displaystyle }$ f$)$의 $평균값{\displaystyle {}_{}}$ y $(\$$displaystyle y_$${\text{avg$$\}\})$를 계산할 때 발생할 수 있습니다. 직관적으로 함수의 평균은 곡선 섹션 아래의 면적을 계산한 다음 해당 섹션의 길이로 나누는 것으로 생각할 수 있습니다.이것은 그래프 용지에 정사각형을 세는 것으로 대충 할 수 있고, 더 정확하게는 적분해서 할 수 있습니다.통합 공식은 다음과 같이 기술됩니다.

$\displaystyle y_{\text{avg}(a,b)=syslogfrac {1}{b-a}\int \displays _{a}^{b}\!f(x)\,files}$

이 경우 적분이 수렴되도록 주의해야 합니다.그러나 함수 자체가 어떤 점에서 무한대인 경향이 있더라도 평균은 유한할 수 있습니다.

각도 및 순환량의 평균

각도, 시간 및 기타 순환 수량을 사용하려면 숫자를 추가하거나 조합하려면 모듈식 산술이 필요합니다.이 모든 상황에서 고유한 수단이 있는 것은 아닙니다.예를 들어 자정 전후의 1시간 시간은 자정 및 정오 모두와 동일합니다.또한 어떤 수단도 존재하지 않을 수도 있다.컬러 휠을 생각해 보세요. 모든 색상 집합에는 평균이 없습니다.이러한 경우에는 어떤 평균이 가장 유용한지 결정해야 합니다.평균화 전에 값을 조정하거나 원형 수량의 평균에 대한 특수 접근 방식을 사용하여 이 작업을 수행할 수 있습니다.

프레셰 평균

프레셰 평균은 표면 또는 보다 일반적으로 리만 다양체의 질량 분포의 "중심"을 결정하는 방법을 제공한다.다른 많은 수단과 달리 프레셰 평균은 요소를 반드시 합산하거나 스칼라로 곱할 수 없는 공간에 정의됩니다.그것은 때때로 카르처 평균으로도 알려져 있다.

스완슨의 법칙

적당히 치우친 ^[5]분포에 대한 평균에 대한 근사치입니다.탄화수소 탐사에 사용되며 다음과 같이 정의된다.

${\displaystyle m=0.3P_{10}+0.4P_{50}+0.3P_{90}}$

여기서₁₀ P, P₅₀ 및₉₀ P는 분포의 10번째, 50번째 및 90번째 백분위수입니다.

기타 수단

「 」를 참조해 주세요.

• 중심 경향
  • 중앙값
  • 모드
• 기술 통계
• 쿠르토시스
• 평균의 법칙
• 평균값 정리
• 모멘트(수학)
• 요약 통계
• 테일러의 법칙

메모들

레퍼런스