카나다키스 통계

이 문서의 주제는 위키피디아의 일반적인 알림 가이드라인을 충족하지 못할 수 있습니다. 주제와는 무관하고 단순한 언급을 넘어 상당한 내용을 다루는 신뢰할 수 있는 2차 출처를 인용함으로써 주제 인지도를 입증할 수 있도록 도와주시기 바랍니다. 알림을 표시할 수 없는 경우 문서가 병합, 리디렉션 또는 삭제될 수 있습니다.출처 : '가나다키스 통계'– 뉴스 · 신문 · 서적 · 학자 · JSTOR (2023년 2월) (이 템플릿 메시지 삭제 방법 및 삭제 시기 확인)

이 기사는 물리학 또는 통계학 전문가의 주의가 필요합니다. 자세한 내용은 토크 페이지를 참조하십시오. Wiki Project Physics 또는 Wiki Project Statistics는 전문가를 채용하는 데 도움이 될 수 있습니다.(2023년 2월)

카니아다키스 통계(--statistics라고도 함)는 고전적인 볼츠만-깁스-샤논 엔트로피(일반적으로 카니아다키스 엔트로피 또는 γ-엔트로피)의^[2][3][4] 상대론적 일반화에 기초한 볼츠만-깁스 통계 ^[1]역학의 일반화이다.2001년 ^[5]그리스의 이탈리아 물리학자 Giorgio Kaniadakis에 의해 도입된 δ-통계 역학은 일반적인 통계 역학의 주요 특징을 보존하고 있으며 최근 몇 년 동안 많은 연구자들의 관심을 끌고 있다.θ-분포는 현재 멱법칙에 따른 통계분포를 포함하는 복잡한 물리적,^[6][7] 자연적 또는 인위적 시스템을 설명할 수 있는 가장 유력한 후보 중 하나로 간주된다.카나다키스 통계는 우주론, 천체물리학,^[8][9] 응축물질, ^[10][11]양자물리학,^[12][13] 지진학,^[14][15] 유전체학,^[18] 경제학,^[16][17] 역학 등의 분야에서 다양한 시스템을 기술하는데 성공적으로 채택되었다.

수학적 형식주의

γ-통계학의 수학적 형식주의는 γ-변형함수, 특히 γ-지수함수에 의해 생성된다.

γ-전위 함수

Kaniadakis 지수(또는 δ-exponential) 함수는 다음과 같이 주어진 지수 함수의 단일 파라미터 일반화입니다.

${\displaystyle \exp _{\kappa }(x)=biggin{case}{\big}{\bigrt {1+\kappa ^{2}x^{\big}}}^{\frac {1}{\kappa }}{\text{if}}}}}0<\kappa<\big (\kappa {\big})\\[6pt]\exp(x)&{\text{if}}}\kappa = 0,\[8pt]\end{case}}$

exp${\displaystyle {}_{}}$- ${\displaystyle {\kappa }_{}}$ x${\displaystyle {}_{}x}$ ) $=$ ${\displaystyle {exp}_{}}$ ${\displaystyle （}$ ${\displaystyle x}$）{ $displaystyle \exp$ _${-\kappa$}(x)=\$exp$ _${\kappa$}($x$를 ${\displaystyle {\mathrm{지정}}_{}}$합니다.

0< < \ $displaystyle$ 0 < \ $kappa$<$1$} 의 「-exponential」도, 다음의 형식으로 쓸 수 있습니다.

${\displaystyle \exp _{\kappa }(x)=\exp {\frac {1}{\kappa }}{\text{arcsinh}}(\kappa x){\exp}Bigg ).}$

Taylor ${\displaystyle {\mathrm{확장}}_{}}$ exp ${\displaystyle {\kappa }_{}}$($（$ ${\displaystyle x}$ ) { $displaystyle \exp$ _${\kappa }(x)}$의 첫 번째 5개 항은 다음과 같습니다.

$\displaystyle \exp _{\kappa }(x)=1+x+{\frac {x^{2}}{2}+(1-\kappa ^{2}){\frac {x^3}}{3!}}+(1-4\kappa^{2}){\frac {x^{4}}{4!}}+\cdots }$

여기서 처음 세 가지는 일반적인 지수 함수와 동일합니다.

기본 속성

γ-exponential 함수에는 다음과 같은 지수 함수의 속성이 있습니다.

$\displaystyle \exp _{\kappa }(x)\in\mathbb {C}^{\infty }(\mathbb {R})}$

${\displaystyle {d}\exp _{\kappa }(x)>0}$

${\displaystyle {d^{2}}{display^{2}}\exp _{\kappa }(x)>0}$

$\displaystyle \exp _{\kappa}(-\infty)=0^{+}$

$\displaystyle \exp _{\kappa }(0)=1}$

$\displaystyle \exp _{\kappa }(+\infty)=+\infty }$

$\displaystyle \exp _{\kappa }(x)\exp _{\kappa }(-x)=-1}$

실수 $\displaystyle$r의 경우 θ-exponential에는 다음 속성이 있습니다.

${\displaystyle [}$ ${\displaystyle {exp}^{}}$ ${\displaystyle {}^{}}$ ( ${\displaystyle x_{}}$ ) ${\displaystyle r_{}}$ ${\displaystyle {=}_{}}$ $exp$ ${\displaystyle (}$ / $（$ ${\displaystyle r}$ x ){ displaystyle { $Big$ [ } \$exp$_ { \ $kappa }$ ( x ){ r }$=$ \ $exp$ _ { \ $kappa$ / $r$} ($r$ x ) $\}$

γ-subsm 함수

카니아다키스 로그(또는 γ-로그)는 일반 로그 함수의 상대론적 단일 매개 변수 일반화이다.

$\displaystyle \ln _{\kappa }(x)=syslog{cases}{\frac {x^{-\kappa}}{2\kappa}}}0 <\kappa <1,\\\[8pt]\ln(x)&{\text{\kappa }}}\pt$

${\displaystyle {\ln }_{}}$- ${\displaystyle {\kappa }_{}}$ (${\displaystyle x}$ ) $=$ ln${\displaystyle \kappa }$ ( x$（$ x $){ displaystyle$ \$ln$_{-\$kappa$}(x)=\$ln _${\kappa$}(x$로, 이는 --연속함수의 역함수입니다.

${\displaystyle \ln _{\kappa }{\big}{\exp _{\kappa }{\big}{\big (}\ln _{\kappa }(x)}=x}$

0< < \ $displaystyle$ 0 < \ $kappa$< $1$} 의 연산도 다음의 형식으로 쓸 수 있습니다.

$\displaystyle \ln _{\kappa }(x)=synh {1}{\kappa }}\sinh {\kappa \ln(x)}}$

${\displaystyle {Taylor}_{}}$ ${\displaystyle {\mathrm{확장}}_{}}$의 첫 번째 3개 항 ln ${\displaystyle {}_{}}$（ ${\displaystyle x}$）{ $displaystyle \ln$_{\$kappa$}($x)$는 다음과 같다.

$\displaystyle \ln _{\kappa }(1+x)=x-{\frac {x^{2}}{2}}+\left(1+{\frac {kappa ^{2}}{2}}\right}{\frac {x}}{3}-\cdots}$

규칙에 따라

$\displaystyle \ln _{\kappa }(1+x)=\sum _{n=1}^{\infty }b_{n}(\kappa),(-1)^{n-1},{\frac {x^{n}}{n}}}}$

${\displaystyle b}$ 1${\displaystyle {}_{}}$( ${\displaystyle )}$ ) $=$ ${\displaystyle 1}$ ( \ $display$ style $b_{1}$ ( \ $kappa$ ) $= 1$ )$$、

${\displaystyle b_{n}(\kappa)(x)=param {case}1&{\text{if}}n=1,\[8pt]{\frac {1}{2}}{\Big (}1-\frac {\kappa}{2}{\big}{\big}}{\big (\frac){{1-{\frac {n-1}{\big}},+,{\frac {1}{2}}{\Big (}1+\kappa {Big}{\big}}{\big (}1+{\frac {kappa }{2}}{\big}...{\big ( ) 1 + {\frac {n-1} {\Big }} & {\text { for }}n > 1,\[8pt]\end {case}}$

${\displaystyle {여기}_{}}$서 b n${\displaystyle {}_{}}$(${\displaystyle 0}$ ) ${\displaystyle =}$ { $display$ b$_$ { $n$} ( 0 ) ${\displaystyle =}$$$${\displaystyle {}_{}}$ n ( -${\displaystyle )}$ ) $=$ n (${\displaystyle \kappa }$ $){$ $display style$ b _ { $n$（ - \ kappa ） =$$b _ { n } ($$\ $kappa$ )$$。Taylor ${\displaystyle {\mathrm{확장}}_{}}$의 ${\displaystyle 첫}$ 번째 항 ln$_$ ( x$$) \ displaystyle $\ln$ _${\kappa$}($x)$는 일반 로그 함수와 동일합니다.

기본 속성

γ-log산술 함수에는 다음과 같은 로그 함수의 속성이 있습니다.

$\displaystyle \ln _{\kappa }(x)\in \mathbb {C}^{\infty }(\mathbb {R}^{+})}$

${\displaystyle\frac {d}\ln _{\kappa }(x)> 0}$

${\displaystyle {d^{2}}{display^{2}}\ln _{\kappa }(x)<0}$

$\displaystyle \ln _{\kappa }(0^{+})=-\infty }$

$\displaystyle \ln _{\kappa }(1)=0}$

$\displaystyle \ln _{\kappa }(+\infty)=+\infty }$

$\displaystyle \ln _{\kappa }(1/x)=-\ln _{\kappa }(x)}$

실수 $\displaystyle$r의 경우 θ-logm에는 다음과 같은 속성이 있습니다.

$\displaystyle \ln _{\kappa }(x^{r})=r\ln _{r\kappa }(x)}$

§-알게브라

총계

임의의${\displaystyle }x{\displaystyle }$, ${\displaystyle yr\mathbb{}}$ R$${\$displaystyle$ x$,y\in$ \$mathbb {R$$}}$및 {\$displaystyle \kappa <1$에 대해 Kaniadakis sum(또는 µ-sum)은 다음 구성 법칙에 의해 정의됩니다.

${\displaystyle x\stackrel{}{}}$ ${\displaystyle \stackrel{}{}}$ ${\displaystyle y\sqrt{\mathrm{}}}$ ${\displaystyle =\sqrt{}}$1 + 2 ${\displaystyle \sqrt{{y\mathrm{}}^{}}}$2 + ${\displaystyle \sqrt{{}^{}}}$ 1${\displaystyle \sqrt{}}$+ ${\displaystyle \sqrt{{y\mathrm{}}^{}}}$ 2 +$$y ${\displaystyle \sqrt{{2\mathrm{}}^{}}}$ x 2 { $display x$ display x $sclackrel${ \ $kappa$} { \ $oplus$} $y = x scrt${ $1$+ \ $kappa$^ { } $y$^ { $2 }$} + $ycrt${ $1$+ \ $kappa ^${ 2 } } } 、

다음 형식으로도 작성할 수 있습니다.

$x$ y $=$ ${\displaystyle 1\frac{\mathrm{}}{}}$ ${\displaystyle \frac{\sin }{}}$ ${\displaystyle \sinh }$（ ${\displaystyle \mathrm{r}}$ ${\displaystyle \mathrm{c}}$ ${\displaystyle \mathrm{si}}$ n ${\displaystyle \mathrm{h}}$（ ${\displaystyle \kappa }$x${\displaystyle }$) + ${\displaystyle \mathrm{r}}$ ${\displaystyle \mathrm{c}}$ ${\displaystyle \mathrm{si}}$ ${\displaystyle \mathrm{n}}$ h${\displaystyle }$（ ${\displaystyle \kappa }$ )${\displaystyle }$y $){$ $style$ x$si$ n h$}{\oplus }}y$={$1 \over$\ $kappa$},\ $sinh \ rm${ $arcsinh}},$ ( $x$)

여기서 보통합은 고전적 $한계치{\displaystyle }$ ${\displaystyle \to }$ ${\displaystyle 0}$ ${\displaystyle \kappa \rightarrow$ 0$\}$ : $x{\displaystyle }$ ${\displaystyle \stackrel{}{\mathrm{}}}$ ${\displaystyle \stackrel{}{}}$ ${\displaystyle =x}$ +$$y { $display stackrel {0}$ {\$oplus$}}$y=x+y}$의 특정$$경우입니다.

θ-sum은 보통합과 마찬가지로 다음과 같은 성질을 가지고 있다.

$\displaystyle\text{1. 연관성:}}\contracrel {\oplus }}{\stackrel {\oplus }}{\stackrel {\oplus }}{\contracrel {\oplus }}}{\contracrel {\kappa }}{\oplus }}}}}}}}$

$displaystyle(디스플레이 스타일)중성 요소:}}\syslog xstackrel {\oplus }}0=0syslog stackrel {\oplus }}x=x}$

$반대편 요소:}}\stackrel {\oplus }}{\stackrel {\oplus }}{\stackrel {\kappa }{\oplus }}x=0}$

${\displaystyle\text{4. 정류성:}}}\syslog xstackrel {\oplus }}y=ysyslog stackrel {\oplus }}x}$

- - rence $\ominus {\displaystyle \stackrel{}{}}$ $（$ { $display$style \ $stackrel$\ $kappa$} { \ $ominus }$ ）는 x${\displaystyle \stackrel{}{}\kappa }$ y ${\displaystyle =}$ ${\displaystyle \stackrel{}{}}$ ${\displaystyle \oplus \stackrel{}{}（}$ -$y ）{$ $display x stackrel$\$kappa$} { \ } y$= x stackrackrel$\ （ \ kappa } { \ } $\}$ $)))))))))$ x x x x x x x x x by by by x x 。

기본 ${\displaystyle {\mathrm{속성}}_{}}$ exp${\displaystyle {\kappa }_{}}$- (${\displaystyle }$- ${\displaystyle x}$ ) exp $x$) ${\displaystyle =}$ 1 {$displaystyle \exp$ _ { $\kappa$} ( - x$)\exp$ _ { $\kappa$ } ( x ) $=$${\displaystyle 1}$} 은$$ 보다 일반적인 표현식의 특수한 경우로서 발생합니다.${\displaystyle {exp}_{}{}_{}{x}_{}}$ ) ${\displaystyle \exp =}$ ${\displaystyle \stackrel{}{}}$ （ ${\displaystyle \stackrel{}{}）\stackrel{}{}}$ 。$}(x420 stackrel {\oplus }}y)$

또한, θ-함수와 θ-sum은 다음과 같은 관계를 나타낸다.

$\displaystyle \ln _{\kappa }(x,y)=\ln _{\kappa }(x){\stackrel {\kappa }{\oplus }}\ln _{\kappa }(y)}$

§ 제품

$x{\displaystyle ,}$ ${\displaystyle y}$ ${\displaystyle r\mathbb{}}$ R$$\$displaystyle$ x$,y$$\in$ \$mathbb {R$ 및 ${\displaystyle \kappa <1$}에 대해 Kaniadakis 곱(또는 "-product")은 다음 구성 법칙에 의해 정의됩니다.

$x$ y ${\displaystyle =}$ ${\displaystyle 1\frac{\mathrm{}}{}}$ ${\displaystyle \frac{\sin }{}}$ ${\displaystyle \sinh }$（ ${\displaystyle 1\frac{\mathrm{}}{}}$ ${\displaystyle \kappa \mathrm{}}$ ${\displaystyle \mathrm{a}}$ r ${\displaystyle \mathrm{c}}$ ${\displaystyle \sinh }$） 、${\displaystyle }$r c sin h ( ${\displaystyle \mathrm{n}}$ x ) 、 r c ${\displaystyle \sin }$ h ( ${\displaystyle \kappa }$ i y )${\displaystyle }$（ $display style$x c sinh$$） { \ $kappa }$ { \ } y = {$1$ \$over \ kappa$} , { 1 \ leftimesin } { $rcs$ } { rcs$}$

여기서 일반 곱은 고전적 $한계치{\displaystyle }$ ${\displaystyle \to }$ ${\displaystyle 0}$ ${\displaystyle \kappa \rightarrow 0$ : $x{\displaystyle \stackrel{\mathrm{}}{}}$ ${\displaystyle \stackrel{}{}}$ y ${\displaystyle =x}$ × y ${\displaystyle =}$ $y$ { $0$} {\$otimes$}}$y= x\times$ y$=xy$의 특정 경우입니다.

-제품은 일반 제품과 마찬가지로 다음과 같은 특성을 가지고 있습니다.

$\displaystyle\text{1. 연관성:}}\times (xtime stackrel {\otimes }}{\stackrel {\otimes }}{\times }}{\times }}{\times }}{\times }}{\timestimes}}}}$

$displaystyle(디스플레이 스타일)중성 요소:}}\sech xkappa stackrel {\otimes }}{\otimes }}I =I {\stackrel {\kappa }{\otimes }x=x\capa ^{-1}\sinh \stackrel {\kappa }{\oplus }x=x}$

$\displaystyle\text{3. 역요소:}}\subline xstackrel {\otimes }{\overline {x}=오버라인 {x}{\stackrel {\otimes}}x=I\quad {text{for}}\subline {x}=\kappa ^{-1}\sin}{\rmin}{\csar}}}}$

${\displaystyle\text{4. 정류성:}}}\sysxstackrel {\otimes }}y=ysstackrel {\times }}x}$

"$display"-$division $⊘$ { $stackrel$\ $kappa$} { \ $oslash }$는 x$x$ y ${\displaystyle =}$ ${\displaystyle x}$ ${\displaystyle \otimes \stackrel{}{}}$ ${\displaystyle \stackrel{}{}\stackrel{}{}}$ { $display$x $stackrel$ \ kappa } { \ $oslash$} y$$= x $stackrel$ { kappa$}$ { \ } { \ $\}\}\}$ { \$linelineline$ x x x x x 。

「-섬$」(\{{\displaystyle \stackrel{}{}}$$displaystyle$$\stackrel\kappa}{\oplus})$ 「-$」({$는, 분배의 법칙에 준거하고 $있습니다{\displaystyle }$.「${\displaystyle z\stackrel{}{}」(\stackrel{}{}\stackrel{}{}\stackrel{}{}}$ y )$$ ${\displaystyle z}$ ${\displaystyle \stackrel{}{}}$ ${\displaystyle 」(\stackrel{}{}}$ )${\displaystyle \mathrm{displaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplay}}$$}}(xvs stackrel {\$oplus }}$y)=(zvs stackrel$ {\kappa }{\otimes $}$x){\stackrel {\oplus$}}(zvs stackrel$ {\kappa }{\$otimes }}}y$

${\displaystyle {기본}_{}}$ ${\displaystyle {\mathrm{속성}}_{}}$ ln ${\displaystyle {}_{}}$（ ${\displaystyle 1}$/${\displaystyle x}$ ${\displaystyle ）}$ $=$ - ln ${\displaystyle \kappa }$ ${\displaystyle x_{}}$ ） {$displaystyle$ \$ln$_{\$kappa }(1/$x)= -\$ln$_{\$kappa }(x$)}는$$ 다음과 같은 보다 일반적인 표현의 특수한 경우에 발생합니다.

$\displaystyle \ln _{\kappa }(x,y)=\ln _{\kappa }(x){\stackrel {\kappa }{\oplus }}\ln _{\kappa }(y)}$

또한 γ-함수와 γ-제품은 다음과 같은 관계를 나타낸다.

$\displaystyle \exp _{\kappa }(x){\stackrel {\kappa }{\otimes }}\exp _{\kappa }(x,+,y)}$

$\displaystyle \ln _{\kappa }(x, {\stackrel {\kappa }{\otimes }},y)=\ln _{\kappa }(x)+\ln _{\kappa }(y)}$

§ - 계산

§-차동

$x(\displaystyle$ x)의 Kaniadakis 미분(또는 δ-차분)은$$ 다음과 같이 정의됩니다.

${\displaystyle {\mathrm{d}}_{}}$ ${\displaystyle {}_{}}$ x x ${\displaystyle =}$ ${\displaystyle d\frac{\mathrm{}}{}}$ ${\displaystyle \frac{{\displaystyle \sqrt{\mathrm{}}}}{}}$1 + ${\displaystyle \frac{{\displaystyle \sqrt{{\kappa \mathrm{}}^{}}}}{}}$ ${\displaystyle \frac{{\displaystyle \sqrt{2{}^{}{}^{}}}}{}}$ ${\displaystyle \frac{{\displaystyle \sqrt{{x\mathrm{}}^{}}}}{}}$ 2$$（ \ $display$ style \ $mathrm${$d$} $_${ \ $kappa }$x$$=$specfrac${ \ $mathrm${ $d }$ 、 , $x }$ { \ $displaystyle${ 1 + \ $kappa$^ { 2$}$} } }$$} 。

$따라서{\displaystyle }$ 함수 f$(x)$의 θ-도함수는 다음과 같은 방법으로 라이프니츠 도함수와 관련된다.

${\displaystyle \frac{d}{}}$f (${\displaystyle \frac{x}{}}$ ) ${\displaystyle \frac{{\mathrm{}}_{}}{}}$ ${\displaystyle {\kappa }_{}}$ ${\displaystyle \frac{{}_{}}{}}$ ${\displaystyle \frac{}{}{}_{}}$df (${\displaystyle \frac{}{}}$x${\displaystyle }$) ${\displaystyle \frac{\mathrm{}}{}}$ ${\displaystyle \frac{f}{}}$( ${\displaystyle \frac{x}{}}$ ) d ${\displaystyle \frac{x}{}}${ $displaystyle${ $frac {$ $f$ ( x ) $}${ \ $mathrm${$d$} { \ $mathrm${ $d$} { \ $mathrm$ { $d$} = \ kappa } ( x ) { \ $f$( x ) } { \ $fx$} { $fx$ } $x$} { $displac$ }

여기서 $where{\displaystyle {}_{}\kappa }$（ ${\displaystyle x\sqrt{\mathrm{}}}$ ) $=$ ${\displaystyle \sqrt{{1\mathrm{}}^{}}}$ + ${\displaystyle \sqrt{{2\mathrm{}}^{}}}$2 x 2 ( { $displaystyle$\ $kappa }$ (x )= $rtrt { 1$ + \ kappa ^ { $2 ^$ {2}}}}는$$ 로렌츠 계수이다.통상 $도함수{\displaystyle \frac{\mathrm{}}{}}$ ${\displaystyle \frac{d}{}}$ f${\displaystyle \frac{}{}}$(${\displaystyle \frac{x}{}}$ )${\displaystyle \frac{d}{}}$ x$$( \ $displaystyle$\$frac${ $d }$ { \ $mathrm { d$${\displaystyle \frac{\}x}{}}$ )는 classical limit$$$d$$$x ( \ $displaystyle$\ $frac${$d }{$ d $}{$\$kappa }의 특정 케이스$입니다.

§ - 내장

카니아다키스 적분(또는 γ-적분)은 다음과 같이 정의된 γ-파생물의 역연산자이다.

${\displaystyle \int }$ ${\displaystyle {}_{}}$ ${\displaystyle \kappa }$ ${\displaystyle \mathrm{dx}}$f${\displaystyle }$(${\displaystyle }$x )${\displaystyle }$= $d$ ${\displaystyle \frac{\sqrt{{}^{}}}{}}$ ${\displaystyle \frac{\sqrt{+}}{}}$ ${\displaystyle \frac{\sqrt{{\kappa \mathrm{}}^{}}}{}}$ 2${\displaystyle }$x ${\displaystyle 2}$f$$( x ) {$display \int$ \$mathrm${ d $} _$ { \ kappa } x ,$f$ ( x ) $= \ int${ $frac$ { $frac$ { d } , x , x } { \ frac { 1 + \ $kappa$^ ^ { $2$} } , x$$} $}$ , x } , $x$} 、

이 값은 표준 $한계치{\displaystyle }$ $→$ $(\displaystyle \kappa$ \$rightarrow$ 0$)$에서 일반 적분을 복구합니다.

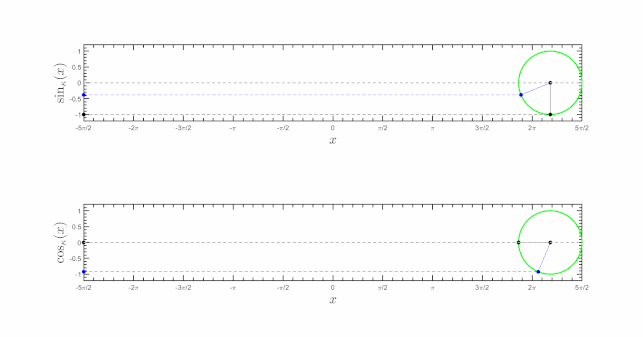
γ-트리고메트리

γ-순환 삼각법

카니아다키스 순환 삼각법(또는 γ-사이클 삼각법)은 다음과 같이 정의된 γ-사이클 사인(또는 γ-사인) 및 γ-사이클 코사인(또는 γ-코사인) 함수에 기초한다.

${\displaystyle {}_{}\sin }$ ${\displaystyle ={exp}_{}}$ ${\displaystyle \frac{=}{}}$ ${\displaystyle \frac{\exp }{}}$ （ ${\displaystyle \frac{i_{}}{}}$x${\displaystyle \frac{}{}}$) - ${\displaystyle \frac{{\exp }_{}}{}}$、 ${\displaystyle \frac{\mathrm{}}{}}$ - ${\displaystyle \frac{i}{}}$x ) ${\displaystyle \frac{2}{}}$i = $sin _$ { \ kappa } ( x ) =$sn frac$ { $exp _$ { \ kappa } ($ix$ ) - \ $exp _$ \ kappa$\}$ ( i ) ,

${\displaystyle {\cos }_{}}$ ${\displaystyle \frac{{\kappa }_{}}{}}$（ ${\displaystyle x}$ )${\displaystyle =}$ exp = ${\displaystyle \frac{{exp}_{}{}_{}}{}}$ ${\displaystyle \frac{i}{}}$x${\displaystyle \frac{）}{}}$ + $exp$ $exp$\ $cos _${ \ kappa } ( x )$$ = ${\displaystyle \frac{\mathrm{}}{}}$ _ { \ $kappa }$( x ) + \ $exp$_ \ $kappa$} ( - $ix$ )$$$,$

여기서 γ-일반화된 오일러 공식은

${\displaystyle {\exp }_{}}$ ${\displaystyle {\mathrm{\kappa \kappa }}_{}（}$ ± ${\displaystyle i}$x ) ${\displaystyle =}$ cos ${\displaystyle \kappa }$ ${\displaystyle x{}_{}}$x${\displaystyle }$) ± ${\displaystyle i_{}}$ sin$κ$ x${\displaystyle }$（ $x$） \ $displaystyle$\ $exp$ _ { \ $kappa$} ( \ $pm ix$ ) = \ $cos$ _ { \ $kappa }$ ( $x )$。

γ-동일 삼각법은 다음과 같이 한계 δ → 0의 특수한 경우인 일반 순환 삼각법의 기본 식을 보존한다.

${\displaystyle \cos _{\kappa }^{2}(x)+\sin _{\kappa }^2}(x)=1}$

${\displaystyle {\sin }_{}{\kappa }_{}}$x （ ${\displaystyle x}$ ${\displaystyle \oplus \stackrel{}{}}$ )${\displaystyle }$y ） ${\displaystyle {}_{}}$ sin ${\displaystyle {\kappa }_{}}$ x${\displaystyle }$（${\displaystyle x}$ ) ${\displaystyle {\cos }_{}}$ ${\displaystyle （}$ ${\displaystyle y）}$ + ${\displaystyle {cos}_{}}$ ${\displaystyle （}$ $）$ sin${\displaystyle }$_ { \ $kappa$} ($x style$\ $sin$ _ { \ $kappa$} { \ （ $x oplus$}$$y$=$ \ $sin$_ $kappa$} \ $cos ）$ _ cos 。

γ-사이클 접선 및 γ-사이클 코탄젠트 함수는 다음과 같이 주어진다.

$\displaystyle \tan _{\kappa }(x)=sin frac {\cos _{\kappa }(x)}{\cos _{\kappa }(x)}}$

${\displaystyle {\cot }_{}\frac{{\kappa }_{}}{}}$ （ x${\displaystyle }$） ${\displaystyle =}$ cos ${\displaystyle \frac{{\kappa }_{}{}_{}}{}}$ ${\displaystyle \frac{\sin }{}}$ （ ${\displaystyle \frac{x_{}}{}}$） sin ${\displaystyle \frac{{\kappa }_{}}{}}$ ${\displaystyle \frac{x}{}}$（${\displaystyle \frac{}{}}$x$$） \ $displaystyle \cot$ _ { \ $kappa$} ( x )$= sn frac$_ { \ cos _ { \ kappa } ( x )$$} $\}$$$。

δ-표준 삼각 함수는 고전 한계 ${\displaystyle \mathrm{\theta }}$ ${\displaystyle \to }$0 {\$displaystyle \kappa \rightarrow$ 0$\}$에서 일반적인 삼각 함수가 됩니다.

γ-역순환함수

카니아다키스 역순환 함수(또는 γ-역순환 함수)는 γ-로그에 관련된다.

$a$ r ${\displaystyle {\mathrm{c}}_{}}$ ${\displaystyle {\mathrm{si}}_{}}$ ${\displaystyle n_{}=}$ - i ${\displaystyle \sqrt{{}^{}}}$（ 1 -${\displaystyle \sqrt{{x\mathrm{}}^{}}}$2 + ${\displaystyle i}$ x$$ { $style {$\ $kappa } _${ \ kappa } ( x ) = -$i$ \ $ln$ _ { \ $kappa$} \ $left$\ $lt${ 1 - x^ { $2$} +$ix$ \$$right )$$,

$a$ r ${\displaystyle {\mathrm{c}}_{}}$ ${\displaystyle {os}_{}}$ s${\displaystyle {}_{}}$（ ${\displaystyle x\sqrt{{}^{}}}$ ) $=$ - ${\displaystyle \sqrt{\mathrm{i}}}$ ${\displaystyle {in}_{}（}$ ${\displaystyle \sqrt{{x\mathrm{}}^{}}}$2${\displaystyle \sqrt{{}^{}}}$-${\displaystyle }$1 + ${\displaystyle x}$）{ $style {\kappa }_{\kappa$ }(x)=-$i\ln$ _${\kappa }\leftrt {x^{2$}-$1}+x\right$

$a$ r ${\displaystyle {\mathrm{c}}_{}}$ t ${\displaystyle {\mathrm{a}}_{}}$ ${\displaystyle {\mathrm{n}}_{}}$( ${\displaystyle x_{}}$( ${\displaystyle x}$ ) $=$ ${\displaystyle i_{}}$ in$κ$ 1 (${\displaystyle \sqrt{\frac{1}{}}}$ - $i$ + ${\displaystyle \sqrt{\frac{i}{}}}$x $){\$)=$i\ln$ _${\kappa$}\$left\trt {1-ix}{1+ix}\right$

$a$ r c ${\displaystyle {\mathrm{o}}_{}}$ ${\displaystyle t_{}}$ ${\displaystyle {}_{}x}$ ) $=$ i ${\displaystyle \sqrt{\frac{\mathrm{in}}{}}{}_{}}$ ${\displaystyle i\sqrt{\frac{}{}}}$x + ${\displaystyle \sqrt{\frac{}{}}}$ i${\displaystyle \sqrt{\frac{x}{}}}$ - $）{\kappa }(x$)=$i\ln$ _${\kappa$}\$left\fracrt {ix+1}{ix-1}\right$

γ-고혈압 삼각법

카니아다키스 쌍곡선 삼각법(또는 γ-하이퍼볼트 삼각법)은 다음과 같이 주어진 γ-하이퍼볼트 사인 및 γ-하이퍼볼트 코사인(cosine)에 기초한다.

${\displaystyle {\sinh }_{}\frac{{\kappa }_{}}{}}$（ x )${\displaystyle \frac{{}_{}=}{}}$ ${\displaystyle \frac{\exp }{}}$ （ ${\displaystyle \frac{x_{}}{}}$ ) - ${\displaystyle \frac{{\exp }_{}{}_{}}{}}$exp （ x${\displaystyle \frac{}{}}$） ${\displaystyle \frac{\mathrm{}}{}}$\ $displaystyle \sinh$ _ { \$kappa$} ( $x$ ) =$snfrac$ {$exp$_ { \ kappa } ($x$ ) - \ $exp$_ \ $kappa$} ( x$)$,

${\displaystyle {\cosh }_{}\frac{{\kappa }_{}}{}{}_{}}$x ${\displaystyle \frac{（}{}}$ x ) ${\displaystyle =}$ exp ${\displaystyle \frac{x}{}}$ x${\displaystyle \frac{(}{\mathrm{}}}$ ) + ${\displaystyle \frac{{exp}_{}}{}}$ ${\displaystyle \frac{（}{}}$ x${\displaystyle \frac{}{}}$） 2$$\ $displaystyle$\ $cosh$ _ { \ $kappa$} （ $x$ ）$= exp _${ \ $kappa$ } ( x ) + \ $exp$_ \ $kappa$$}$ ( $x )$ ,

여기서 δ-Uler 공식은

${\displaystyle {\exp }_{}}$ ${\displaystyle {\kappa }_{}}$（ ± ${\displaystyle x}$） ${\displaystyle =}$ $cosh$ ${\displaystyle \kappa （}$ x )${\displaystyle }$± ${\displaystyle \sinh )}$ （ x$$） \ $displaystyle$\ $exp$ _ { \ $kappa$}$$= \$cosh _${ \ $kappa$} ($x$ ) \ $pm$ \ $sinh$ _ { \ $kappa$} ($x$ )$$}

γ-하이퍼볼릭 탄젠트 및 γ-하이퍼볼릭 코탄젠트 함수는 다음과 같습니다.

$\displaystyle \tanh _{\kappa }(x)=synh _{\kappa }(x)}{\cosh _{\kappa }(x)}}$

${\displaystyle {}_{}\coth }$ $=$ ${\displaystyle \frac{{\cosh }_{}}{}}$ ${\displaystyle \frac{\kappa }{}}$ （ x ${\displaystyle \frac{）}{}}$ ${\displaystyle \frac{{sinh}_{}}{}}$ ${\displaystyle \frac{{}_{}}{}}$ ${\displaystyle \frac{x}{}}$ ${\displaystyle \frac{（}{}}$ x$$）{ $display$style \$coth$ _${\kappa$}(x)=$cosh _{\kappa$}($x)}{\sinh$ _${\kappa$

γ-쌍곡선 삼각함수는 고전적 한계 ${\displaystyle \mathrm{\theta }}$ ${\displaystyle \to }$0 ${\displaystyle$ \$kappa$ \$rightarrow$0$\}$에서 일반적인 쌍곡선 삼각함수가 됩니다.

δ-Eler 공식 및 ${\displaystyle \mathrm{속성}}$ exp ${\displaystyle {\delta }_{}}$δ ${\displaystyle （}$ - ${\displaystyle x_{}}$ ) ${\displaystyle \exp }$ $=$1${\displaystyle }${$displaystyle \exp$ _ { \kappa$}$ ( - x )\$exp _${ \$kappa$} ( x$)=$1}에서 δ-유도 삼각법의 기본 표현은 다음과 같습니다.

${\displaystyle \cosh _{\kappa }^{2}(x)-\sinh _{\kappa }^{2}(x)=1}$

γ-역쌍곡선 함수

카니아다키스 역 쌍곡선 함수(또는 γ-역 쌍곡선 함수)는 γ-로그 산술에 관련지어집니다.

$a$$$$}}+x\$right$)\},$

$a$ r ${\displaystyle {\mathrm{c}}_{}}$ c ${\displaystyle o_{}}$ s h${\displaystyle {}_{}（}$ x ) $=$ ${\displaystyle {\mathrm{in}}_{}x\sqrt{{}^{}}}$ x x ( ${\displaystyle \sqrt{{x\mathrm{}}^{}}2}$- 1${\displaystyle }$+$$x ){$style {\kappa }_${\$kappa$ }(x)=\$ln$_{\$kappa$}\$left\ln$ rt ${x^{2$}-$1}+x\right$

$a$ r c ${\displaystyle {\mathrm{t}}_{}}$ ${\displaystyle {\mathrm{a}}_{}}$ ${\displaystyle n_{}}$ ${\displaystyle {\mathrm{h}}_{}（}$ ${\displaystyle x}$ ) $=$ $κ$ ${\displaystyle 1\sqrt{\frac{\mathrm{}}{}}}$ (${\displaystyle \sqrt{\frac{}{}}}$1 + ${\displaystyle \sqrt{\frac{x}{1}}}$- ${\displaystyle \sqrt{\frac{\mathrm{}}{}}}$ $){\$ }(x)=\$ln$ _${\kappa }\leftfrac$ \ $ln$ \ $frac { 1$ + $x}$ { 1 - $x}$ \$right )$,

$a$ r ${\displaystyle {\mathrm{c}}_{}}$ ${\displaystyle {\mathrm{o}}_{}}$ t ${\displaystyle h_{}}$ ${\displaystyle {}_{}x}$ ) $= in$ ${\displaystyle \kappa \sqrt{\frac{\mathrm{}}{}}}$1${\displaystyle \sqrt{\frac{}{}}}$( ${\displaystyle \sqrt{\frac{\mathrm{}}{}}}$- ${\displaystyle \sqrt{\frac{x}{}}}$ 1 +${\displaystyle \sqrt{\frac{}{}}}$x $){$ style {\kappa$}_{\kappa$}(x)=\$ln$ _${\kappa$ }\$left$rt ${1-x}{1+x}\right$

는 다음 관계가 유효합니다.

$=$$}$$}}}\right$

$=$$si$$}}}}\right$

$=$$+x$$}}$ {$x}$ \$$right$$} } 。

γ-사이클릭 및 γ-하이퍼볼릭 삼각함수는 다음과 같은 관계에 의해 연결됩니다.

${\displaystyle {}_{}\mathrm{si}}$ n$=$ - ${\displaystyle in}$ ${\displaystyle {\mathrm{h}}_{}（}$ i ${\displaystyle {\mathrm{x}}_{}}$ ){ $displaystyle { sin$}_${\kappa$}($x)=-ijavrm {sinh}_{\kappa$}($ix$

$c$ ${\displaystyle o_{}}$ s${\displaystyle {}_{}}$（${\displaystyle x}$ ) ${\displaystyle =}$ ${\displaystyle {\mathrm{c}}_{}}$ s ${\displaystyle h_{}}$（ ${\displaystyle i}$ ${\displaystyle x}$）{ $displaystyle {$ cos }_${\kappa$}(x) =$secrm${$cosh}_{\kappa$}($ix$ ,

${\displaystyle {\mathrm{t}}_{}}$ ${\displaystyle {\mathrm{a}}_{}}$ ${\displaystyle n_{}}$( ( (${\displaystyle x}$ ) $=$ - ${\displaystyle {\mathrm{i}}_{}}$ a ${\displaystyle {\mathrm{n}}_{}}$ h${\displaystyle {}_{}}$( ${\displaystyle i}$ （ ${\displaystyle i}$x$$){$displaystyle$ {$tan}_{\kappa }(x$)=-$i440rm {tanh}_{\kappa$}($ix$

$c$ ${\displaystyle o_{}}$ t${\displaystyle {}_{}}$（${\displaystyle x}$ ) $=$ ${\displaystyle {\mathrm{}}_{}}$ ${\displaystyle {\mathrm{c}}_{}}$ ${\displaystyle {\mathrm{o}}_{}}$ t ${\displaystyle h_{}}$（ ${\displaystyle i}$ x$$ $displaystyle { coth$ }_${\kappa$}(x)=$i440rm {coth}_{\kappa$}($ix$

${\displaystyle {}_{}a}$ r ${\displaystyle {\mathrm{c}}_{}}$ ${\displaystyle {\mathrm{si}}_{}}$ $=$ - ${\displaystyle {\mathrm{i}}_{}}$ ${\displaystyle r{\mathrm{}}_{}}$ c ${\displaystyle {\mathrm{si}}_{}}$ ${\displaystyle {\mathrm{n}}_{}}$ ${\displaystyle h_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle i}$x $){$ $style {rm {arcsin}}_{\kappa }(x$)=-$i, {\rm$ {$arcsinh}}_{\kappa$}($ix$

$a$ r ${\displaystyle {\mathrm{c}}_{}}$ ${\displaystyle {\mathrm{c}}_{}}$ ${\displaystyle o_{}}$ s${\displaystyle {}_{}}$(${\displaystyle }$x )${\displaystyle }$- ${\displaystyle {\mathrm{i}}_{}}$ ${\displaystyle r{\mathrm{}}_{}}$ ${\displaystyle {\mathrm{c}}_{}}$ ${\displaystyle {\mathrm{o}}_{}}$ ${\displaystyle {\mathrm{s}}_{}}$ ${\displaystyle h_{}}$( ${\displaystyle i}$ x$$ $style${rm ${arccos}_{\kappa$}($x)\neq -i,{\rm {arccosh}}_{\kappa$}($ix$

${\displaystyle {\mathrm{a}}_{}}$ r c ${\displaystyle {\mathrm{t}}_{}}$ a ${\displaystyle n_{}}$( ( (${\displaystyle x}$ ) $=$ - ${\displaystyle {\mathrm{i}}_{}}$ c ${\displaystyle {\mathrm{t}}_{}}$ ${\displaystyle {\mathrm{a}}_{}}$ ${\displaystyle {\mathrm{n}}_{}}$ ${\displaystyle {\mathrm{h}}_{}}$( ${\displaystyle i}$ ( i x $){$ $style {rm {arctan}_{\kappa$}($x$)=-$i, {\rm$ {$arctanh}}_{\kappa$}($ix$

${\displaystyle {\mathrm{a}}_{}}$ r ${\displaystyle {\mathrm{c}}_{}}$ ${\displaystyle {\mathrm{c}}_{}}$ ${\displaystyle o_{}}$ t${\displaystyle {}_{}}$（${\displaystyle x}$ ) $=$ ${\displaystyle i{\mathrm{}}_{}}$ ${\displaystyle {\mathrm{a}}_{}}$ ${\displaystyle {\mathrm{r}}_{}}$ ${\displaystyle {\mathrm{c}}_{}}$ ${\displaystyle {\mathrm{o}}_{}}$ ${\displaystyle {\mathrm{t}}_{}}$ ${\displaystyle h_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle i}$ ${\displaystyle x}$style {$rm {arccot}_{\kappa$}(x)=$i,$ {\$rm {arccoth}}_{\$kappa }($ix$

카니아다키스 엔트로피

Kaniadakis 통계는 Kaniadakis γ-엔트로피를 기반으로 하며, 이는 다음을 통해 정의된다.

${\displaystyle S_{\kappa}{\big (}pbigbig)}=-\sum _{i}p_{i}\ln _{i}{\big}=\sum _{i}p_{i}\ln _\kappa }{big}{p}{p} {\frac1}$

$여기$서 p ${\displaystyle =}$ { ${\displaystyle p_{}}$ i ${\displaystyle {}_{}p}$ ( ${\displaystyle x_{}}$i${\displaystyle }$) ; ${\displaystyle x}$R ; ${\displaystyle i}$ ${\displaystyle =1}$,${\displaystyle }$2,${\displaystyle }$.${\displaystyle }$,${\displaystyle N}$ ;${\displaystyle \underset{i}{}}$ ${\displaystyle \underset{}{}{}_{}}$ ${\displaystyle i_{}}$ $= 1 }$ ({ $displaystyle$ p$=\{p_i}$ ; $x\in \mathbb {R}$ ;$i=1,2,N\sum_i}$ )$_sum_i}$ < <\ $style$0 \ $leq$\$kappa$<$1$}는 엔트로픽인덱스입니다

카니아다키스 γ-엔트로피는 열역학적으로 안정적이며 연속성, 최대성, 일반화된 부가성 및 확장성의 섀넌-킨친^[19][20] 공리에 따른다.

카나다키 분포

카니아다키스 분포(또는 γ-분포)는 적절한 제약 조건 하에서 카니아다키스 엔트로피의 최대화에 의해 도출된 확률 분포이다.이와 관련하여, 실험 멱함수 법칙에 따른 통계 분포와 관련된 다양한 현상학을 분석하기 위해 몇 가지 확률 분포가 나타난다.

§-지수 분포

γ-가우스 분포

①-감마 유통

②-Weibull 분포

①-로지스틱 분포

카니아다키스 적분 변환

§-랩레이스 트랜스폼

Kaniadakis Laplace 트랜스폼(또는 "-Laplace 트랜스폼)은 일반 Laplace 트랜스폼의 µ-deformed 적분 트랜스폼입니다."-Laplace 변환은 복소수 영역에서 실수 변수$t$의 $함수$$f{\displaystyle {}_{}}$(\displaystyle$$$$t$)$를 새로운 함수 F($s$)로 변환합니다(${\displaystyle {복소수}_{}}$ $변수{\displaystyle }$s\$displaystyle$ f_${\kappa$$}($$s$$)).$이 '통합형 트랜스폼'^[21]은 다음과 같이 정의됩니다.

$\displaystyle F_{\kappa }(s)={f(t)\}(s)=\int _{,0}^{\infty }\!f(t),[\exp _{\kappa }(-t)]^{s},dt}$

역 "-Laplace 변환은 다음과 같습니다.

${\displaystyle f(t)=cal {L}_{\kappa }^{-1}\{F_{\kappa }(s)\}(t)=c\frac {1}{2\piiiiii}}\int _{c+i\infty}^{c+i\infty}\!F_{\kappa}(s),{\frac {\exp _{\kappa }(t)}{s}}{\sqrt {1+\kappa ^{2}t^{2}}}},ds}}$

일반 Laplace 변환과 그 역변환은 ${\displaystyle \mathrm{\kappa }}$ ${\displaystyle \to }$0 \ $displaystyle$\ $kappa$\ $rightarrow$0$$으로 회복됩니다.

특성.

$f{\displaystyle }$(${\displaystyle t}$ ) ${\displaystyle =}$ ${\displaystyle {\mathcal{}}_{}^{}}$ ${\displaystyle {}_{}^{}}$ -${\displaystyle {}_{}^{}{1}_{}^{}}$ { ${\displaystyle F_{}}$ ${\displaystyle {}_{}}$ (${\displaystyle s}$ ) ${\displaystyle \}}$ (${\displaystyle t}$) { $display style$ f$(t$) =$fcal {L} _${ \ $kappa$} { { {$F$ _ { \$kappa$ } \ { F _ { \ kappa } } \ { F$$_$$ { s } } ( t ) 및${\displaystyle }g{\displaystyle }$ (${\displaystyle t}$ )${\displaystyle {}_{}^{}=}$ L ${\displaystyle \kappa }$ - ${\displaystyle {}_{}）。}$및 각각의 "-라플라스 $변환{\displaystyle {}_{}}$ F${\displaystyle {}_{}}$ (${\displaystyle s}$) { $displaystyle F_{\kappa$} ($s$ )$$ ${\displaystyle G_{}}$"${\displaystyle }$( s ) \ $displaystyle$G_{\$kappa }$( $s$) ${\displaystyle {the}_{}}$ 。다음 표는 "-라플라스 ^[21]변환의 주요 속성을 나타내고 있습니다.

"-Laplace" 변환 속성

소유물	${\displaystyle f(t)}$	$\displaystyle F_{\kappa}(s)$
선형성	${\displaystyle a,f(t)+b,g(t)}$	${\displaystyle a,F_{\kappa}(s)+b,G_{\kappa}(s)}$
시간 스케일링	${\displaystyle f(at)}$	$({displaystyle {1}{a}},F_{\kappa /a}({\frac {s}{a}})})$
주파수 시프트	${\displaystyle f(t),[\exp _{\kappa }(-t)]^{a}}$	$\displaystyle F_{\kappa}(s-a)}$
파생상품	${\displaystyle {d,f(t)}{dt}}$	${\displaystyle s,{\cal {L}}_{\kappa }\left\{\frac {f(t)}{\sqrt {1+\kappa ^{2}t^{2}}}}\right\}-f(0)}$
파생상품	${\displaystyle {frac {d}{dt}}, {\displayrt {1+\kappa ^{2}t^{2}},f(t)}$	$\displaystyle s,F_{\kappa}(s)-f(0)}$
시간 영역 통합	${\displaystyle {\frac {1}{1+\kappa ^{2}t^{2}}}}},\int _{0}^{t}f(w)f(w)f}$	${\displaystyle {1}{s}},F_{\kappa}(s)}$
	${\displaystyle f(t),[\ln(\exp _{\kappa }(t)}}}^{n}}$	${{displaystyle(-1)^{n}{\frac {d^{n}F_{\kappa}(s)}{ds^{n}}}}$
	${\displaystyle f(t),[\ln(\exp _{\kappa }(t)})]^{-n}}$	${{s}{+\infty}{n}\int_{w_{n}}^{+\infty}{n-1}개...\int _{w_{3}}^{+\infty }dw_{2}\int _{w_{2}}^{+\infty}dw_{1},F_{\kappa}(w_{1})$
디랙 델타 함수	$\displaystyle \displays ( t-\displays )$	${\displaystyle [\exp _{\kappa }(-\display )]^{s}$
헤비사이드 단위	${\displaystyle u(t-\displaystyle)}$	${\displaystyle {\frac {sparrt {1+\kappa ^{2}\capa ^{2}\capa ^{2}},[\exp _ {\kappa }(-\kappa })^{s}}$
멱함수	${\displaystyle t^{\nu -1}}$	$({displaystyle {s^{2}-\kappa ^{2}\nu ^{2}},{\frac {Gamma _{\frac {\kappa }{s}},{\nu +1}}},{\frac {\nu }},{\frac {s}}, {s},}}}$
멱함수	$(\displaystyle t^{2m-1},\\m\in Z^{+})$	$(2m-1) displaystyle!}{\capa _{j=1}^{m}\left[s^{2}-(2j)^2}\kappa^{2}\right]}}}$
멱함수	$(\displaystyle t^{2m},\\m\in Z^{+})$	${\displaystyle {(2m)!,s}{\display_{j=1}^{m+1}\left[s^{2}-(2j-1)^{2}\kappa^{2}\right]}}}$

후자의 표에 제시된 δ-라플라스 변환은 기존의 한계치 $\theta {\displaystyle }$ ${\displaystyle \to }$ $(\displaystyle \kappa \rightarrow$ 0$)$에서 대응하는 통상적인 라플라스 변환으로 환원됩니다.

§ - Fourier 트랜스폼

카니아다키스 푸리에 변환(또는 γ-Fourier 변환)은 일반 푸리에 변환의 γ-변형 적분 변환으로, γ-대수 및 γ-calculus와 일치합니다."-Fourier 변환은 다음과 ^[22]같이 정의됩니다.

${\displaystyle {F}_{\kappa }_{f(x)}={1 \over {\warrt {2,\pi }}\int \infty ^{+\infty }f(x),\exp _\kappa }(-x\otimes _{\kappa }_d })^{d } {d } } i }$

라고 고쳐 쓸 수 있다.

${\displaystyle {F}_{\kappa }_{f(x)}={1 \over {\calrt {2,\pi }}\int \infty ^{+\infty }f(x), {\exppari,x_{\kappa \},\opha}\infty \infty } \inf(xpa)\crpa) \inf(xpa) \ } } } } } } int _{-over } } } } }$

$여기$서${\displaystyle {}_{}}$x { ${\displaystyle arcsinh\frac{\mathrm{}}{}{}_{}}$} ${\displaystyle {}_{}}$ 1 ${\displaystyle \kappa \mathrm{}}$ ${\displaystyle \mathrm{a}}$ ${\displaystyle \mathrm{r}}$ ${\displaystyle \mathrm{c}}$ ${\displaystyle \sin }$ h (${\displaystyle }$${\displaystyle \kappa }$ x )$$（ { $display$ x _ { \ { \ $kappa$ \ $}$） 、 { \ rm { $arcsinh }$ 、 （ \ ${\displaystyle \mathrm{kappa<img\; alt="\{\backslash displaystyle\; x\_\{\backslash \{\backslash kappa\; \backslash \}\}=\{\backslash frac\; \{1\}\{\backslash kappa\; \}\}\backslash ,\{\backslash rm\; \{arcsinh\}\}\backslash ,(\backslash kappa\; \backslash ,x)\}"\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/e5abc370f125cc1d1a5306c479e3a8827ce62337"\; style="vertical-align:\; -1.838ex;\; width:22.32ex;\; height:5.176ex;">}}$ }${\displaystyle }$） 、 ${\displaystyle displaydisplaydisplaydisplaydisplaydisplaydisplay\mathrm{}}$ $display{\displaystyle {}_{}}$ display display displaydisplaydisplay ${\displaystyle {\mathrm{display}}_{}}$ ${\displaystyle \mathrm{displaydisplaydisplay}}$ ${\displaystyle display\frac{\mathrm{}}{}}$ displaydisplay ${\displaystyle \mathrm{displaydisplaydisplay}}$ ${\displaystyle \mathrm{displaydisplaydisplaydisplaydisplay}}$ ${\displaystyle \mathrm{displaydisplaydisplaydisplaydisplaydisplaydisplaydisplay}}$ $displaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplay$"-Fourier 변환에서는 감쇠계수$displaystyle {1$+\kappa ^{2},x^{2${\displaystyle \sqrt{\mathrm{}}}\}\}\})$ 외에$$x\displaystyle$$x$$및$$${\displaystyle \sqrt{{x\mathrm{}}^{}}}$\$displaystyle \mega}$ $파라미터$도 변형함으로써 점근적으로 로그 주기적인 동작이 발생합니다.

γ-Fourier 변환의 커널은 다음과 같습니다.

${\displaystyle h_{\kappa }(x,\obega)=parc frac {\expari,x_{\kappa \},\obega _{\kappa \}}}{\carrt {1+\kappa ^{2},x^{2}}}}}}}}$

역 "-Fourier 변환은 다음과 ^[22]같이 정의됩니다.

${\displaystyle {F}_{\kappa }[{\hat {f}(\obe rt {2,\pi }}\int \infty _{-\infty }\int ^{-\infty }{\hat {f}}(\hat {f},\exp{\kappa }) _kappa }$

u${\displaystyle {}_{}}$(${\displaystyle }$( ${\displaystyle x}$ ) ${\displaystyle =}$ ${\displaystyle 1\frac{\mathrm{}}{}}$ ${\displaystyle \frac{\kappa }{}}$ ${\displaystyle \cosh （}$ ${\displaystyle \kappa }$ ln ${\displaystyle ）}$ （ $x$） =$display u _$ { \ kappa } { \ $kappa }$ = $cosh$ {$Big$ ( } \ $kappa$\ $ln$( x ) { \ $Big$}$$} , , , , $functions{\displaystyle {}_{}}$ functions functions functions functions functions functions functions functions functions::::::::::::::::::::::::::::::::::::::::::::::::::::^[22]

γ-여러 함수의 Fourier 변환

	${\displaystyle f(x)}$	$(\displaystyle {F}}_{\kappa}[f(x)](\mega)}$
스텝 함수	${\displaystyle\theta(x)}$	$(\displaystyle {2,\pi }},\displaystyle (\obe)+{1 \over {\beatrt {2,\pi }},i,\obe _{\kappa \}}})$
변조	${\displaystyle \cos _{\kappa}(astack stackrel {\kappa}{\oplus }}x)}$	$(\displaystyle {\pi \over2}}, u_{\kappa }(\exp _{\kappa }(a),\left(\displaystyle (\mega +a)+\display(\mega -a)\right)})$
$원인{\displaystyle }$»(\$displaystyle \kappa)$ - 지수$$	$\displaystyle \theta (x),\exp _{\kappa }(-a stackrel {\kappa }{\otimes }}x)$	${\displaystyle {1 \over {2 , \pi }} {1 \over a_{\kappa \}} +i , \ 메가 _{\kappa \}}$
$대칭{\displaystyle }$ ${\$ { $displaystyle \kappa }$ - exponential$$	$\displaystyle \exp _{\kappa}(-a stackrel {\kappa}{\otimes }} x )$	$({displaystyle {2 \over \pi }}, {a_{\kappa \}}, {\kappa \}}, {\kappa \}, {\kappa \}, {\mega _{\kappa \}, {\})$
일정한	${\displaystyle 1}$	$(\displaystyle {2,\pi }},\displaystyle (\mega)}$
$§$ ${\displaystyle$ \kappa$}$ - ${\displaystyle \mathrm{페이저}}$	${\displaystyle \exp _{\kappa},(a's stackrel {\otimes }}x)^{i}}$	${\displaystyle {2,\pi }},u_{\kappa}(\exp_{\kappa}(a),\displaystyle(\mega -a)}$
임퓨설스	$\displaystyle \syslog(x-a)}$	${\displaystyle {1 \over {2 , \pi }}{\exp _{\kappa },(\otimes }a)^{i} \over u_{\kappa }\left(\exp _{\kappa },(a)\오른쪽)}}$
시그넘	Sgn ${\displaystyle x}$) {$디스플레이$ 스타일 $(x)}$	$({displaystyle {2 \over \pi }},{1 \over i,\obega _{\kappa \}}})$
직사각형	${\displaystyle\Pi\left({x\over a}\오른쪽)}$	$({displaystyle {2 \over \pi }}, a_{\kappa \}, {\rm {\kappa}}_{\kappa}({stackrel\kappa}{\otimes }a})})$

δ-변형 버전의 푸리에 변환은 다음 표에 요약되어 있듯이 일반 푸리에 변환의 주요 특성을 유지합니다.

§ - Fourier 속성

${\displaystyle f(x)}$	$(\displaystyle {F}}_{\kappa}[f(x)](\mega)}$
선형성	$\displaystyle {\cal {F}_{\kappa }[\alpha \f(x)+\alpha \,g(x)],{\cal {F}_{\kappa },{\cal {F}+\cal {F},{\cal {F}_{\kappa }(x})$
스케일링	${\displaystyle {F}_{\kappa }\left[f(\alpha \x)\right]((오메가)={1 \over \alpha },{\cal {F}}_{\kappa ^{\prime }}\left[f(x)\right](오메가 ^{\primega })$ ${\displaystyle \mathrm{여기}}$서 $\kappa {\displaystyle {}^{}}$ $=$ / ${\displaystyle \alpha }$ \ $displaystyle \kappa ^{\prime$ } =\$kappa$ $/\alpha }$ 및$$ ${\displaystyle {\omega \mathrm{}}^{}}$ $=$($a$ /${\displaystyle \kappa }$ ) ${\displaystyle \sinh }$ ${\displaystyle \mathrm{r}}$ ${\displaystyle \mathrm{c}}$ ${\displaystyle \sin }$h (${\displaystyle ）}$ /${\displaystyle {}^{}a{}^{}}$) $sinh cs$ { $display styleft$\ ^ { \ } } 。
$§$ ${\displaystyle$ \kappa$}$ - ${\displaystyle \mathrm{스케일링}}$	${\displaystyle {F}_{\kappa }\left[f(\alpha {stackrel {\otimes }x}\right](오메가)={1 \over \alpha _{\kappa \}, {\cal {F}_{\kappa }[f(x)\f(x)\f(\f(x)} } } } } } } = {1 }$
복소 활용	${\displaystyle {\cal {F}_{\kappa }{\big [}f(x){\big }{\ast }(\mega)={\cal {F}_{\kappa }{\big [}(-\big [)}$
이중성	${\displaystyle {F}_{\kappa}{\cal {F}_{\kappa}{\big]}(\big [}f(x){\big }}(\nu){\big }}(\mega)=fbig\mega}$
리버스	${\displaystyle {F}_{\kappa }\left[f4x]\right]((오메가)={F}_{\kappa }[f(x)](-\mega)}$
$§$ ${\displaystyle$ \kappa$$$}$ - $주파수$ 이동	${\displaystyle {F}_{\kappa}\left[\exp _{0}{\stackrel {\otimes }x)^{i}f(x)\right](\obmega)={F}_{\kappa}[f(x)\light](\displaycal {F}(\cal {\kappa }) }$
$§$ ${\displaystyle$ \kappa$$$}$ - $시간$ ${\displaystyle \mathrm{이동}}$	${\displaystyle {F}_{\kappa }\left[f(x,{\stackrel {\oplus }},x_{0}\right]((오메가)=\exp _{\kappa }({\stackrel {kappa },{0})\cal})$
$§$ (\$displaystyle$ \$kappa)$ $-파생물$의 변환	$\displaystyle {\cal {F}_{\kappa }\left[{\frac {d,f(x)}\right](\d_{\kappa }x})=i,\opha _{\{\kappa \},{\cal {F}_{\kappa }[f(x)\mega }$
$§$ ${\displaystyle$ \kappa$}$ - 변혁의 ${\displaystyle \mathrm{유도체}}$	${\displaystyle {frac {d} {\kappa } {\cal {F} {\kappa }}, {\cal {F(x)} {\kappa }, {\cal {F}_{\kappa }, {\cal {\kappa }, {\cal {\cal {\kappa }\kappa \}, f(x)\right](\mega)}$
적분 변환	$\displaystyle {\cal {F}_{\kappa }\left[\int \infty }\light ^{x}f(y),dy\right]={1 \over i,\Omega _{\kappa \}{\cal {F}_{\kappa }[\pi }(\cal {\cal {\kappa },\ci},\},\}, {\},\}, {\},\}, {\in},\},\},$
$§$ ${\displaystyle$\kappa$}$ - ${\displaystyle \mathrm{콘볼루션}}$	${\displaystyle {F}_{\kappa }\left[(f,{\stackrel {\kappa}{\stackast }}(x)(x)\right](\cal {F}_{\kappa}{f(x)\cal } {\cal }} {\cal }} {\f}$ ${\displaystyle \mathrm{여기}}$서${\displaystyle }$( f ${\displaystyle ⊛⊛\stackrel{}{}g\stackrel{}{}}$) (${\displaystyle x}$ ) ${\displaystyle \underset{}{\overset{}{\mathrm{=}}}}$ $displaystyle$( $f$, { \ $stackrel$\ $kappa$ { \ $scast$} { , $g$) = \$int$ \ $intime$_ { - \ $infty$} \ conna _ { $-$ $infty } y ( x$ $g$ ${\displaystyle ),}$
변조	${\displaystyle {F}_{\kappa }\left[f(x),g(x)\right]((오메가)={1 \over {\displayrt {2,\pi }}\left[f(x)\right], {\stack {kappa } {CAL}$

후자의 표에 제시된 δ-Fourier 변환의 특성은 고전적 한계치 ${\displaystyle \mathrm{\theta }}$ ${\displaystyle \to }$0(\$displaystyle \kappa \rightarrow$ 0$)$에서 대응하는 일반 푸리에 변환으로 감소합니다.

「 」를 참조해 주세요.

• 조르지오 카니아다키스
• 카니아다키스 분포
• 카니아다키스 θ-지수 분포
• 카니아다키스 γ-가우스 분포
• 카니아다키스 γ-감마 분포
• 카니아다키스 δ-Weibull 분포
• 카니아다키스 δ-로지스틱 분포
• 카니아다키스 γ-얼랑 분포

레퍼런스

• 이 문서에는 CC BY 3.0 라이센스로 제공되는 텍스트가 포함되어 있습니다.

외부 링크

• Giorgio Kaniadakis Google Scholar 페이지
• arXiv.org의 Kaniadakis 통계 정보