검벨 분포

곰벨

확률밀도함수
누적분포함수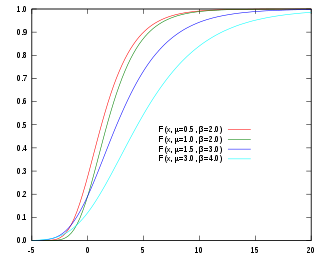
표기법	${\displaystyle {\text{Gumbel}}(\mu,\beta )}$
매개변수	${\displaystyle \mu ,}$ ${\displaystyle \mu,}$ 위치$$(실제) > 0 ${\displaysty$> $0,}$축척 (리얼)
지지하다	${\displaystyle x\in \mathbb {R}}$
PDF	${\displaystyle {\frac {1}{\beta }}e^{-(z+e^{-z})}$ 여기서 $z$ = ${\displaystyle x}$ -${\displaystyle \frac{\mu }{}}$ ${\displaystyle \frac{}{}}$ ${\displaystyle$z = {\$frac {x-\mu}{\$beta }}
CDF	${\displaystyle e^{-e^{-(x-\mu )/\beta }}$
의미하다	${\displaystyle \mu +\beta \gamma }$ 여기서 γ ${\displaystyle \gamma}$는 오일러-마스케로니 상수입니다.
중앙값	${\displaystyle \mu -\beta \ln(\ln 2)}$
모드	${\displaystyle \mu}$
분산	${\displaystyle {\frac {\pi^2}}{6}}\ beta ^{2}}$
왜도	${\displaystyle {\frac {12{\sqrt {6}}\,\zeta(3)}{\pi^{3}}\approx 1.14}$
절두술	${\displaystyle {\frac {12}{5}}$
엔트로피	${\displaystyle \ln(\beta)+\gamma +1}$
MGF	${\displaystyle \Gamma (1-\beta)e^{\mut}$
CF	${\displaystyle \Gamma (1-i\beta)e^{i\mut}$

확률 이론 및 통계학에서 Gumbel 분포(타입-I 일반화 극단값 분포라고도 함)는 다양한 분포의 여러 표본의 최대(또는 최소) 분포를 모형화하는 데 사용됩니다.

이 분포는 지난 10년간의 최대치 목록이 있는 경우 특정 연도의 강의 최대치 분포를 나타내는 데 사용될 수 있습니다.이것은 극심한 지진, 홍수 또는 다른 자연 재해가 발생할 가능성을 예측하는 데 유용합니다.최대치의 분포를 나타내는 Gumbel 분포의 잠재적 적용 가능성은 극한값 이론과 관련이 있으며, 이 이론은 기본 표본 데이터의 분포가 정규 또는 지수형인 경우 유용할 가능성이 높다는 것을 나타냅니다.이 글에서는 Gumbel 분포를 사용하여 최대값의 분포를 모형화합니다.최소값을 모형화하려면 원래 값의 음수를 사용합니다.

Gumbel 분포는 일반화된 극단값 분포(Fisher-Tippet 분포라고도 함)의 특정한 경우입니다.로그-바이불 분포 및 이중 지수 분포(Laplace 분포를 나타내기 위해 때때로 사용되는 용어)라고도 합니다.곰퍼츠 분포와 관련이 있습니다. 밀도가 원점에 대해 처음으로 반영된 후 양의 반선으로 제한되면 곰퍼츠 함수가 얻어집니다.

다항로짓 모형의 잠재 변수 공식(불연속 선택 이론에서 일반적)에서 잠재 변수의 오차는 Gumbel 분포를 따릅니다.두 Gumbel 분포 랜덤 변수의 차이가 로지스틱 분포를 가지므로 유용합니다.

검벨 분포는 에밀 줄리어스 검벨 (1891–1966)^[1][2]의 이름을 따서 지어졌습니다.

정의들

Gumbel 분포의 누적 분포 함수는

${\displaystyle F(x;\mu,\beta)=e^{-e^{-(x-\mu)/\beta }}\,}$

표준검벨분포

표준검벨분포는 누적분포함수를 갖는 $\mu$ = 0 ${\displaystyle \mu$ = $},$ $\beta$ = ${\displaystyle 1}${\$displaystyle$ \$$beta = $1}$인 경우입니다.

${\displaystyle F(x)=e^{-e^{(-x)}}\,}$

확률밀도함수

${\displaystyle f(x)=e^{-(x+e^{-x}}}}$

이 경우 모드는 0, 중위수는 -${\displaystyle \ln }$ ⁡${\displaystyle }$( ${\displaystyle \ln }$ ⁡${\displaystyle }$( ${\displaystyle 2}$)${\displaystyle }$≈ ${\displaystyle 0.3665}$ ${\displaystyle$ -\$ln(\ln(2))\대략$ 0$.3665$ $평균$은 γ ≈ ${\displaystyle 0.5772}${\$displaystyle \gamma \대략 0.5772}($오일러-마스케로니 상수), 표준 편차는 π${\displaystyle }$/ ${\displaystyle 6}$ ≈ ${\displaystyle \mathrm{1.2825입니다.}}$ ${\displaystyle \pi$ / ${\sqrt {6}}\대략 1.2825}$

n > 1에 대한 누적수는 다음과 같습니다.

${\displaystyle \kappa _{n}=(n-1)!\zeta(n)}$

특성.

모드는 μ이고 중위수는 $\mu$ -${\displaystyle \beta }$ ${\displaystyle \ln }$⁡${\displaystyle (\ln }$ ⁡ 2 ${\displaystyle ),}$ ${\displaystyle \mu$ -$\beta \ln \left(\ln 2\right)}$이며 평균은 다음과 같습니다.

${\displaystyle \mathrm{}\mathrm{E}}$ ${\displaystyle \mathrm{(}X)}$ $=$ ${\displaystyle \mathrm{\mu }}$ +$γ$ ${\displaystyle \beta }$ ${\displaystyle \operatorname {E$)=\$m$eta $},$

여기서 γ ${\displaystyle \gamma}$는 오일러-마스케로니 상수입니다.

표준 편차 σ ${\displaystyle$\sigma }은(는) $\beta$ π${\displaystyle }$/ ${\displaystyle 6}$ ${\displaystyle$\beta \$pi$/${\sqrt {6}}$이므로 $\beta$ = σ 6 /${\displaystyle }$π ≈ ${\displaystyle 0.78}$ σ입니다${\displaystyle .}$ ${\displaystyle$\beta =\sigma {\$sqrt {6}}/\pi$\approx $0.78\$sigma입니다$.$

${\displaystyle x}$ = μ ${\displaystyle$ x=\$mu}$인 모드에서 $F$$($${\displaystyle x;}$ μ,${\displaystyle \beta )}$ ${\displaystyle F(x;\mu,\$beta$)}$의 값은$$$\beta$ 값에 관계없이 $e$ -${\displaystyle 1^{}}$ ≈ ${\displaystyle 0.37}$ ${\displaystyle e^{-1}\$approx $0.37}$이 됩니다.${\displaystyle$\beta $.}$

${\displaystyle {G1}_{},...,{Gk}_{}}$ ${\displaystyle G_{1},...,G_{k}}$가 매개 변수$$(${\displaystyle \mu ,\beta )}$ ${\displaystyle (\mu,\beta )}$인 iid Gumbel 랜덤 변수라면, ${\displaystyle max}${${\displaystyle {G1}_{},...,{Gk}_{}}$ ${\displaystyle \max\{G_{1},...,G_{k}\}$도 매개 변수$$(${\displaystyle \mu }$ ${\displaystyle +}$ ${\displaystyle \beta }$ ${\displaystyle \ln }$⁡ k${\displaystyle ,\beta }$)$${\$displaystyle$(\$mu +\beta \ln$ k$,\beta )}$인 Gumbel 랜덤 변수입니다$.$

${\displaystyle {G1\mathrm{}}_{}}$ ${\displaystyle {G2\mathrm{}}_{}}$ $...{\displaystyle G_{1}, G_{2},$ ...인 경우$}$모든 자연수 ${\displaystyle k_{}}$ ${\displaystyle {}_{}}$$displaystyle k}$에 대해 ${\displaystyle 최대}$ $G1$ $..., Gk}$ $- β ln$$⁡$ k {\$displaystyle$ \max$\{$$G_${1}, $...,$$G_${k$}\}-\beta \ln$ k$}$이(${\displaystyle {가}_{}}$) G1 {\$displaystyle$ G_{$1}}$과(와) 동일한 분포를 갖도록 iid 랜덤 변수임$,$${\displaystyle {G1\mathrm{}}_{}}$ ${\$는 반드시 Gumbel에 스케일 매개 변수 $\beta {\displaystyle }$ ${\displaystyle \beta}($실제로 공임인 k>1의 두 개의 서로 다른 값만 고려하면 충분함)와 함께 분포됩니다.$$

관련분포

• $X$ ${\displaystyle X}$에 Gumbel 분포가 있는 경우 Y가 양수이거나 X가 음수인 경우 이와 동등하게 Gompertz 분포가 있는 Y = -X의 조건부 분포입니다.Y의 cdf G는 식 $G{\displaystyle }$( ${\displaystyle y}$ )${\displaystyle }$= ${\displaystyle P}$( ${\displaystyle Y}$ ${\displaystyle \le }$ ${\displaystyle y}$ )${\displaystyle }$= ${\displaystyle P}$( ${\displaystyle X}$ ≥${\displaystyle }$- ${\displaystyle y}$ ∣ ${\displaystyle \mathrm{X}}$ ${\displaystyle \le }$ 0 )${\displaystyle }$=${\displaystyle }$( ${\displaystyle F}$( ${\displaystyle 0}$)${\displaystyle }$- F${\displaystyle }$( -${\displaystyle y}$)${\displaystyle }$)${\displaystyle }$/ ${\displaystyle \mathrm{F}}$( 0${\displaystyle }$) ${\displaystyle G(y$) = P $(Y\leq$y) =$$P$(X\geq -y\mid X\leq$0) = ($F (0)$ - $F ($y$) }$ / F$(0$) } 에 의해 결정됩니다. 결과적으로 ${\displaystyle \mathrm{밀도}}$는 g${\displaystyle }$(${\displaystyle y}$ ) =${\displaystyle f}$ (${\displaystyle }$-${\displaystyle y}$ ) / ${\displaystyle \mathrm{F}}$(${\displaystyle }$0$$) {\$displaystyle g($y) = $f$(-$y)$ / F ($0$ : 곰퍼츠와 관계가 있습니다.밀도는 반사된 Gumbel 밀도에 비례하며 양의 반선으로 제한됩니다.^[4]
• X가 평균이 1인 지수 분포 변수이면 -log(X)는 표준 Gumbel 분포를 가집니다.
• $X{\displaystyle }$~ ${\displaystyle \mathrm{Gumbel}}$ (${\displaystyle {}_{}}$ ${\displaystyle X_{}}$ ${\displaystyle \beta )}$ ${\displaystyle X\sim \mathrm {Gumbel} (\alpha _{X},\beta )}$ 와$$ $Y{\displaystyle }$~ ${\displaystyle \mathrm{Gumbel}}$ ${\displaystyle ({}_{}}$ ${\displaystyle Y_{}}$,${\displaystyle {}_{}\beta }$) ${\displaystyle Y\sim \mathrm {Gumbel} (\alpha _{$${\displaystyle Y_{}}$$},\beta )}$ 가 독립적이면$$ ${\displaystyle X}$- $Y{\displaystyle }$~ ${\displaystyle \mathrm{Log}}$는 ${\displaystyle \mathrm{i}}$ ${\displaystyle \mathrm{c}}$(${\displaystyle {}_{}}$ ${\displaystyle X_{}}$- α ${\displaystyle {}_{}}$ ${\displaystyle \beta }$) ${\$$}$($$로지스틱 분포 참조).
• $X{\displaystyle ,}$ ${\displaystyle Y}$ ~${\displaystyle \mathrm{Gum}}$ ${\displaystyle \mathrm{bel}}$(${\displaystyle \alpha }$,${\displaystyle \beta )}$ ${\displaystyle X,$ Y$\sim \mathrm {Gumbel} (\alpha,\$beta $)}$ 이 독립적이면 X${\displaystyle }$+ ${\displaystyle Y}$ ≁ ${\displaystyle \mathrm{Log}}$는 ${\displaystyle \mathrm{틱}}$ ${\displaystyle (2}$ ${\displaystyle \alpha }$,${\displaystyle \beta }$) ${\displaystyle X+Y\nsim \mathrm {Logistic} (2\alpha,\$beta $)}.$$E{\displaystyle }$( ${\displaystyle X}$+ Y${\displaystyle }$)${\displaystyle }$= ${\displaystyle 2}$ ${\displaystyle \alpha }$+ ${\displaystyle 2}$ ${\displaystyle \beta }$ γ ≠ 2 ${\displaystyle \alpha }$ = E${\displaystyle }$( ${\displaystyle L}$ ${\displaystyle o}$ ${\displaystyle \mathrm{g}}$ i ${\displaystyle \mathrm{i}}$ i ${\displaystyle \mathrm{c}}$ ${\displaystyle (2}$ ${\displaystyle \alpha ,}$ ${\displaystyle \beta }$) ${\displaystyle$E$(X+Y$) = $2\alpha$ +2$\$beta$\neq 2\alpha$ =$E\left(\mathrm {Logistic} (2\alpha,\beta)\right$ 보다 일반적으로, 독립적인 Gumbel 랜덤 변수들의 선형 조합의 분포는 GNIG와 GIG 분포로 근사될 수 있습니다.^[5]

일반화된 다변량 로그 감마 분포와 관련된 이론은 Gumbel 분포의 다변량 버전을 제공합니다.

발생 및 적용

Gumbel에 따르면 지수 분포를 따르는 랜덤 변수 표본의 최대값(또는 마지막 순서 통계량)^[8]에서 표본 크기의 자연 로그를 뺀 값이 표본 크기가 증가함에 따라 Gumbel 분포에 근접합니다.

구체적으로, ρ${\displaystyle }$(${\displaystyle x)}$= ${\displaystyle {}^{}}$- ${\displaystyle x^{}}$ ${\displaystyle \rho ($x) = $e^{-x}$ 를 $x$${\$$displaystyle x}$ 의 확률 분포라 하고, $Q$ (x) = ${\displaystyle 1}$ - ${\displaystyle e^{}}$ x $displaystyle Q(x$) = 1 - $e^{-x}$ 의 누적 분포라고 합니다.그러면 x ${\displaystyle x}$의 $N개$의$${\$displaystyle$N}개의$$ 실현 $중$에서$$X {\$displaystyle$ X}개보다$$$$ 작은 최대값이 X ${\$$displaystyle$ $X$$}$개보다 작습니다$.$ 따라서 최대값 $x{\displaystyle \stackrel{}{}}$~ ${\$개의 누적 분포가 다음을$$ 만족합니다.

${\displaystyle P({\tilde {x}}-\log(N)\leq X)=P({\tilde {x}}\leq X+\log(N)=[Q(X+\log(N))]^{N}=\left(1-{\frac {e^{-X}}{N}}\right)^{N}}}$

큰 $N{\displaystyle }$ ${\displaystyle N}$의 경우 오른쪽이 $e{\displaystyle {}^{}}$ -${\displaystyle {{}^{}}^{}}$(${\displaystyle {{}^{}}^{}}$- ${\displaystyle {X^{}}^{}}$)로 수렴합니다${\displaystyle {{}^{}}^{}}$ ${\displaystyle$ e$^{-e^{($ - $X)}}$

그러므로 수문학에서 굼벨 분포는 일일 강우량과 하천 방류량의 월별 및 연간 최대치와 같은 변수를 분석하고 가뭄을 설명하는 데 사용됩니다.^[3][9]

검벨은 또한 추정치가 사건의 확률에 대한 r ⁄(n+1)(여기서 r은 데이터 시리즈의 관측치 값의 순위 번호이고 n은 총 관측치 수)는 분포 모드 주변의 누적 확률에 대한 편향되지 않은 추정치입니다.따라서 이 추정기는 종종 플롯 위치로 사용됩니다.

수론에서 굼벨 분포는 정수의^[10] 임의 분할에 있는 항의 수와 최대 소수 간격 및 소수 별자리 사이의 최대 간격의 추세 조정된 크기의 근사치입니다.^[11]

검벨 재매개변수화 기술

기계 학습에서 Gumbel 분포는 때로 범주형 분포로부터 표본을 생성하는 데 사용됩니다.이 기술은 "검벨-맥스 트릭"이라고 불리며 "재파라미터화 트릭"의 특별한 예입니다.^[12]

구체적으로, ($$π ${\displaystyle 1_{}}$…,${\displaystyle }$π ${\displaystyle n_{}}$ ${\displaystyle (\pi _{1},\ldots,\pi _{n}}}$를 모두 0이 아닌 음이 아니라고 하고, ${\displaystyle {g1}_{}}$ ${\displaystyle \dots ,{gn}_{}}$ ${\displaystyle g_{1},\ldots,g_{n}$을 Gumbel(0, 1)의 독립적인 표본이라고 한 다음, 루틴 적분으로,

즉, ${\displaystyle \arg }$⁡ ${\displaystyle \underset{}{max}}$i ( ${\displaystyle {gi}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle log}$ ⁡ π${\displaystyle {}_{}}$i )${\displaystyle }$~ ${\displaystyle \text{범주형}}$(π j π i ∑ ${\displaystyle {\frac{i_{}}{}}_{}}$ ) ${\displaystyle {}_{}}${\$displaystyle \arg \max _{i}(g_{i}+\log \pi_{i})\sim${\$text{Categorical}}\left({\frac${\$pi _{j}}{\sum _{i}\pi$ _${i}\right)_{j}}$

이와 동등하게, $임의$의 x ${\displaystyle 1_{}}$ ${\displaystyle ...,}$x ${\displaystyle n_{}}$ ∈ ${\displaystyle R}$ ${\displaystyle x_{1$}, $...,x_{n}\in \mathbb {R}}$에서$,$ 우리는 다음과 같이 볼츠만 분포로부터 표본을 추출할 수 있습니다.

관련 방정식은 다음과 같습니다.^[13]

• $x{\displaystyle }$~ ${\displaystyle \mathrm{Exp}}$⁡${\displaystyle (}$λ${\displaystyle )}$ ${\displaystyle x\sim \operatorname {Exp}(\lambda )}$인 경우,$$(${\displaystyle }$- ${\displaystyle \ln }$ ⁡ x -${\displaystyle }$γ )${\displaystyle }$~ ${\displaystyle \text{Gumbel}}$ (${\displaystyle }$-${\displaystyle }$γ${\displaystyle }$+ ${\displaystyle \ln }$ ⁡ λ, ${\displaystyle (-\ln x-\gamma )}\sim {\text{Gumbel}(-\gamma +\ln \lambda$
• ${\displaystyle \arg }$ ⁡${\displaystyle max}$ i (${\displaystyle \underset{}{}{gi}_{}}$ +${\displaystyle {}_{}\log }$ ⁡ π${\displaystyle {\frac{{}_{}}{}}_{}}$i${\displaystyle {}_{}}$)${\displaystyle }$~ ${\displaystyle \text{범주형}}$(${\displaystyle {}_{}\sum }$ ${\displaystyle {\frac{\underset{}{}}{}}_{}}$ π ${\displaystyle {\frac{i_{}}{}}_{}}$) j ${\displaystyle$\arg $\max$ _${i}(g_{i}+\log \pi_{i})\sim {\text{Categorical}}\left({\frac {\pi$ _${j}}{\sum$ _${i}\pi$ _${i}\right$
• ${\displaystyle \underset{}{max}}$ ${\displaystyle \underset{}{i}}$( ${\displaystyle {gi}_{}\underset{}{+\; 로}그}{\displaystyle }$ ${\displaystyle \underset{}{}}$ ${\displaystyle i_{}}$ )${\displaystyle {}_{}}$~${\displaystyle \text{Gumbel}}$ ${\displaystyle \underset{}{(}}$ 로그${\displaystyle \underset{}{}}$ (${\displaystyle \underset{}{}\sum }$ ${\displaystyle \mathrm{i}}$ ${\displaystyle \underset{}{\pi }}$ ${\displaystyle i_{}}$ ${\displaystyle ),}$ 1${\displaystyle }$) ${\displaystyle$ \$max _{i}(g_{i}+\log \pi_{i})\sim {\text{gumbel}}\left(\log \left(\sum$ _${i}\pi$ _${i}\right$)},$1\right)}.$즉, Gumbel 분포는 최대 안정 분포 계열입니다.
• ${\displaystyle \mathbb {E} [\max _{i}(g_{i}+\beta x_{i})]=\log \left(\sum _{i}e^{\beta x_{i}\right)+\gamma .}$

변량생성

Gumbel 분포의 분위함수(역누적분포함수)인 Q${\displaystyle (p)}$ ${\displaystyle Q(p$는 다음과 같이 주어집니다.

${\displaystyle Q(p)=\mu -\beta \ln(-\ln(p)),}$

랜덤 변수 $U{\displaystyle }$ ${\displaystyle$ $Q(U$$)}$를 구간$$${\displaystyle }$(${\displaystyle 0,}$ ${\displaystyle 1)}$ ${\displaystyle$ ($0$$,$1) {\displaystyle $($0, 1$)}$의 균일한 분포에서 그릴 때 $변수{\displaystyle }$$$ $Q{\displaystyle (U)}$ ${\displaystyle \mu}$ 및 $\beta {\displaystyle }$ ${\displaystyle \beta}$ 매개 변수가$$ 있는 Gumbel 분포가 있습니다$$$.$

확률지

소프트웨어 이전 시대에는 확률 종이를 사용하여 Gumbel 분포를 그려냈습니다(그림 참조).이 논문은 누적 분포 함수 $F{\displaystyle }$ ${\displaystyle F}$의 선형화를 기반으로 합니다.$$

${\displaystyle -\ln[-\ln(F))]={\frac {x-\mu}{\beta }}$

이 논문에서 수평축은 이중 로그 스케일로 구성됩니다.수직 축은 선형입니다.종이의 가로축에 $F$ ${\displaystyle F}$를 그리고 세로축에 $x{\displaystyle }$ ${\displaystyle x}$ - 변수를$$ 플롯함으로써 분포는 기울기 1${\displaystyle }$/ ${\displaystyle \beta }${\$displaystyle$/\$beta}$인 직선으로 표현됩니다$.$ CumFreq와 같은 분포 맞춤 소프트웨어를 사용할 수 있게 되자 분포를 플롯하는 작업이 쉬워졌습니다.

참고 항목

• Type-2 Gumbel 분포
• 극치론
• 일반화된 극값 분포
• 피셔-티펫-그네덴코 정리
• 에밀 줄리어스 검벨

참고문헌

외부 링크