얼랑 분포
Erlang distribution| 확률밀도함수  | |||
| 누적분포함수 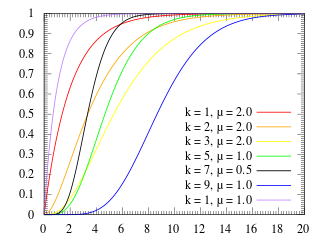 | |||
| 파라미터 | 모양. ( 0 、 \ \\ ( 0 , \ ) .: β / \ \=/ \ ,} 척도 | ||
|---|---|---|---|
| 지지하다 | |||
| CDF | |||
| 의미하다 | |||
| 중앙값 | 단순 폐쇄 양식 없음 | ||
| 모드 | |||
| 분산 | |||
| 왜도 | |||
| 예: 첨도 | |||
| 엔트로피 | |||
| MGF | - )- ( \ \( 1 - { \ { t } { \ { t } } ){ - } ( t \ < \ da ) | ||
| CF | |||
Erlang 분포는 연속 확률 분포의 2 파라미터 패밀리입니다.x"[ , ")\ x \ [ , \ 를 합니다.다음 두 가지 파라미터가 있습니다.
- 양의 k \ k "shape" 및
- ""을 나타내는 양의 실수 \환율의 역수인 "",β (\가 대신 사용될 수 있습니다.
Erlang 분포는 각각 1/ { 1을 k\ k}개의 지수 변수의 합입니다.마찬가지로 포아송 공정의 k번째 사건까지의 시간 분포이며, 비율이{일 때 k = 1 { k일 , 그 분포는 지수 분포로 단순화된다.Erlang 분포는 분포의 모양이 검출되는 감마 분포의 특수한 경우이다.
Erlang 분포는 A. K. Erlang에 의해 개발되었으며, 스위칭 스테이션의 오퍼레이터에게 동시에 발신될 가능성이 있는 전화의 수를 조사합니다.전화 트래픽엔지니어링에 관한 이 작업은 큐잉 시스템에서의 일반적인 대기시간을 고려하도록 확장되었습니다.분포는 확률적 과정 분야에서도 사용된다.
특성화
확률밀도함수
Erlang 분포의 확률 밀도 함수는 다음과 같습니다.
파라미터 k를 쉐이프 파라미터라고 파라미터{\\를 rate 파라미터라고 합니다.
대체적이지만 동등한 매개변수화에서는 속도 매개변수 β / \ \ 의 역수인 척도 β {\ displaystyle \ displayda = 1 displayda}를 사용합니다.
척도 β {\가 2일 때 분포는 2k 자유도를 갖는 카이 제곱 분포로 단순해집니다.따라서 자유도의 짝수에 대한 일반화 카이 제곱 분포로 간주할 수 있습니다.
누적분포함수(CDF)
Erlang 분포의 누적 분포 함수는 다음과 같습니다.
어디γ{\displaystyle \gamma}것은, 불완전 감마 함수 및 P{P\displaystyle}것은, 본격적으로 감마 함수.그 CDF도 표현할 수 있다.
Erlang-k
그 Erlang-k 유통(어디에 k은 긍정적인 정수)Ek({\displaystyle E_{km그리고 4.9초 만}(\lambda)}는에 의해 정의된 설정 k에서 PDF의 얼랑 분포를 보여 준다.[1]예를 들어, Erlang-2 유통 x에 E2(μ))λ k=e− λ xλ ≥ 0{\displaystyle E_{2}(\mu)={\lambda ^{km그리고 4.9초 만}x}e^{-\lambda)}\quad{\mbox{에}}x,\lambda \geq 0}일 경우, f로(x;2, λ){\displaystyle f(x;2,\lambda)} 같기 때문이다.
중앙값
점근 팽창은 [2]계수를 계산할 수 있고 한계를 알 [3][4]수 있는 Erlang 분포의 중위수에 대해 알려져 있습니다.근사치는 (- {\입니다.right) 즉, 평균 보다 낮습니다.[5]
Erlang 분포 랜덤 변수 생성
Erlang 분포 랜덤변수는 다음 [6]공식을 사용하여 균일하게 분포된 난수( [ , \ U \ [ , )에서 생성할 수 있습니다.
적용들
대기 시간
일부 평균 비율로 독립적으로 발생하는 사건은 포아송 공정에 의해 모형화됩니다.이벤트가 k회 발생하는 대기 시간은 Erlang 분포입니다.(특정 시간 내 사건 발생 횟수에 대한 관련 질문은 포아송 분포로 설명됩니다.)
착신 콜간의 시간을 측정하는 Erlang 분포는, 착신 콜의 예상 기간과 조합해 사용하고, Erlang 단위로 측정된 트래픽 부하에 관한 정보를 작성할 수 있습니다.이는 차단된 콜이 중단되는지(Erlang B 공식) 또는 서비스될 때까지 큐잉되는지(Erlang C 공식)에 대해 이루어진 다양한 가정에 따라 패킷 손실 또는 지연의 확률을 판단하기 위해 사용할 수 있습니다.Erlang-B 및 C 공식은 여전히 콜센터 설계 등의 응용 프로그램의 트래픽모델링에 사용되고 있습니다.
기타 응용 프로그램
암 발생의 연령 분포는 종종 얼랑 분포를 따르지만, 형태와 척도 매개변수는 각각 운전자 사건의 수와 그 [7][8]사이의 시간 간격을 예측한다.보다 일반적으로, Erlang 분포는 다단계 [9][10]모델의 결과로 셀 주기 시간 분포의 좋은 근사치로 제안되어 왔다.
그것은 또한 상호 구매 시간을 기술하는 [11]데 비즈니스 경제학에서 사용되어 왔다.
특성.
- X~ ( ,){ X \{ } ( , \ )일 경우 ~ ( k , 는 , )입니다.
- ~ (1 ,) { X \{ } ( k { , \ ) } Y~ ( 2 , ) { Y \ \{} ( k 2 , \ 2 , \ lam )의 , \ dislang } xda + b )) 。 X은(는) 독립적입니다.
관련 분포
- Erlang 분포는 각각 지수 분포를 갖는 동종 의존적이고 동일한 분포 랜덤 변수의 합계의 분포입니다.X의 기대의 일을 발생할 장기 금리는 역, 그것은,λ/k{X\displaystyle,}.{\displaystyle \lambda /k.}은 얼랑 분포의(나이 구체적인 사건)률, k의에 있x1,{\displaystyle k>, 1,}monotonic, 0에서 x로 증가할{\displaystyle x}=0.{)x 0,} ~ { \ } { \ [12] x}는 무한대 경향이 있습니다.
- 즉, ~ ( { \{Exponential}(\의
- 즉, ~ ( { \{Exponential}(\의
- PDF 및 누적분포함수의 요인 함수 때문에 모수 k가 양의 정수인 경우에만 Erlang 분포가 정의됩니다.실제로 이 분포는 Erlang-k 분포라고 불리기도 합니다(예를 들어 Erlang-2 분포는 k=인 Erlang 분포입니다).감마 분포는 요인 함수 대신 감마 함수를 사용하여 k를 임의의 양의 실수로 허용함으로써 Erlang 분포를 일반화합니다.
- 즉, k가 이고 ( , ) ,{ X \{} ( , \ )인 경우 X ( , { X \ \{ } ( , } ( k , lambda )
- ~ ( ) { U \ \operatorname } ( \ lambda) v ~ ( , 、 V \ \{ } ( n , \ )일 +~ )
- Erlang 분포는 Pearson 유형 III 분포의[citation needed] 특수한 경우입니다.
- Erlang 분포는 카이 제곱 분포와 관련이 있습니다.X~ ( , ), { \{ } ( , \ ) }인 , 2 X .\\ _ { 2 k }^{ 2 }。[citation needed]
- Erlang 분포는 포아송 공정에 의한 포아송 분포와 관련이 있습니다. n i i { S _ { n } = \ _ { i=}^{ _ { } {\、 { X _ { } \ \ { ( \ ) )。그리고.n n에 차이를 구하면 포아송 분포를 얻을 수 있습니다.
「 」를 참조해 주세요.
메모들
- ^ "h1.pdf" (PDF).
- ^ Choi, K. P. (1994). "On the medians of gamma distributions and an equation of Ramanujan". Proceedings of the American Mathematical Society. 121: 245–251. doi:10.1090/S0002-9939-1994-1195477-8. JSTOR 2160389.
- ^ Adell, J. A.; Jodrá, P. (2007). "On a Ramanujan equation connected with the median of the gamma distribution". Transactions of the American Mathematical Society. 360 (7): 3631. doi:10.1090/S0002-9947-07-04411-X.
- ^ Jodrá, P. (2012). "Computing the Asymptotic Expansion of the Median of the Erlang Distribution". Mathematical Modelling and Analysis. 17 (2): 281–292. doi:10.3846/13926292.2012.664571.
- ^ Banneheka, BMSG; Ekanayake, GEMUPD (2009). "A new point estimator for the median of gamma distribution". Viyodaya J Science. 14: 95–103.
- ^ Resa. "Statistical Distributions - Erlang Distribution - Random Number Generator". www.xycoon.com. Retrieved 4 April 2018.
- ^ Belikov, Aleksey V. (22 September 2017). "The number of key carcinogenic events can be predicted from cancer incidence". Scientific Reports. 7 (1). doi:10.1038/s41598-017-12448-7. PMC 5610194. PMID 28939880.
- ^ Belikov, Aleksey V.; Vyatkin, Alexey; Leonov, Sergey V. (2021-08-06). "The Erlang distribution approximates the age distribution of incidence of childhood and young adulthood cancers". PeerJ. 9: e11976. doi:10.7717/peerj.11976. ISSN 2167-8359. PMC 8351573. PMID 34434669.
- ^ Yates, Christian A. (21 April 2017). "A Multi-stage Representation of Cell Proliferation as a Markov Process". Bulletin of Mathematical Biology. 79 (1): 2905–2928. doi:10.1007/s11538-017-0356-4.
- ^ Gavagnin, Enrico (14 October 018). "The invasion speed of cell migration models with realistic cell cycle time distributions". Journal of Theoretical Biology. 79 (1): 91–99. arXiv:1806.03140. doi:10.1016/j.jtbi.2018.09.010.
- ^ C. Chatfield와 G.J. Goodhard: "에를랑 인터바이즈 타임에 따른 소비자 구매 모델"; 미국 통계 협회 저널, 1973년 12월, Vol.68, 페이지 828-835
- ^ Cox, D.R.(1967) 갱신 이론, p20, Methuen.
레퍼런스
- Ian Angus "Erlang B 및 Erlang C의 개요", 텔레매니지먼트 #187 (PDF 문서 - 용어 및 공식과 짧은 전기 포함)
- Stuart Harris "Erlang Calculations vs. 시뮬레이션"











![{\displaystyle (1-k)\psi (k)+\ln \left[{\frac {\Gamma (k)}{\lambda }}\right]+k}](https://wikimedia.org/api/rest_v1/media/math/render/svg/274f6ef68b61a8f859d3c49d5ba4a0fec6590ed8)
















![{\displaystyle U\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/66966a6f68e58c668e96ae0c3d72967076188f6e)

 경우
경우

 (는) 독립적입니다.
(는) 독립적입니다.




 경우 X
경우 X









