누적빈도분석

Cumulative frequency analysis
누적 빈도 분포, 조정된 누적 확률 분포 및 신뢰 구간

누적 빈도 분석은 기준 값보다 작은 현상의 발생 빈도를 분석하는 것이다. 그 현상은 시간이나 공간에 따라 다를 수 있다. 누적 빈도는 비초과의 빈도라고도 한다.

특정 현상(특성)이 특정 값 이하인 빈도에 대한 통찰력을 얻기 위해 누적 빈도 분석을 수행한다. 이것은 현상과 관련된 상황을 설명하거나 설명하거나, 홍수 보호와 같은 계획적 개입에 도움이 될 수 있다.[1]

이 통계 기법은 과거에 얼마나 자주 일어났는지를 기준으로 홍수 같은 사건이 미래에 다시 일어날 가능성을 확인하는 데 사용할 수 있다. 그것은 겨울과 여름을 더 건조하게 만드는 기후 변화 같은 것들을 가져오도록 적응될 수 있다.

원칙

정의들

빈도 분석은[2] 관측된 현상이 특정 범위에서 얼마나 자주 또는 얼마나 자주 발생하는지를 분석하는 것이다.

주파수 분석은 가변현상 X에 대한 관측 데이터 X1, X2, X3 . .의N 길이 N 기록에 적용된다. 기록은 시간 의존적(예: 한 지점에서 측정한 강우량) 또는 공간 의존적(예: 면적에서의 농작물 수확량) 또는 그 밖의 것일 수 있다.

기준값 Xr의 누적 주파수 M은Xr 관측값 X가 Xr보다 작거나 같은 주파수다.

상대적 누적 주파수 Fc는 다음에서 계산할 수 있다.

FcXr = M / N

여기서 N은 데이터 수입니다.

간단히 말해서 이 표현은 다음과 같이 주목할 수 있다.

Fc = M / N

When Xr = Xmin, where Xmin is the unique minimum value observed, it is found that Fc = 1/N, because M = 1. On the other hand, when Xr=Xmax, where Xmax is the unique maximum value observed, it is found that Fc = 1, because M = N. Hence, when Fc = 1 this signifies that Xr is a value whereby all data are less than or equal to Xr.

백분율로 방정식은 다음과 같이 읽는다.

Fc(%) = 100M / N

확률추정

누적 빈도수로부터

X의 누적 확률 Pc가 Xr보다 작거나 같을 경우, 누적 주파수 M에 기초하여 여러 가지 방법으로 추정할 수 있다.

한 가지 방법은 상대적 누적 주파수 Fc를 추정치로 사용하는 것이다.

또 다른 방법은 드물게 X가 관측된 최대 Xmax보다 큰 값을 가정할 가능성을 고려하는 것이다. 이는 누적 주파수 M을 N 대신 N+1로 나눌 수 있다. 그러면 추정치는 다음과 같이 된다.

Pc = M / (N+1)

분모에 대한 다른 제안도 존재한다(플롯 포지션 참조).

순위결정기법별

순위 누적 확률

데이터 순위를 매겨 확률 추정이 쉬워진다.

X의 관측 데이터가 오름차순으로 배열된 경우(X12 ≤ X ≤ X3 ≤ . . . X, 최소 첫 번째 및 최대 마지막N) 리(李)는 관측 Xi의 순위 번호로, 여기서 adfix i는 오름차순 데이터 범위의 일련번호를 나타내는 경우, 누적 확률을 다음과 같이 추정할 수 있다.

Pc = Ri / (N + 1)

반면 X의 관측 데이터가 최대 첫 번째와 최소 마지막인 내림차순으로 배열되고 Rj가 관측치 Xj의 순위 번호인 경우 누적 확률은 다음과 같이 추정할 수 있다.

Pc = 1 − Rj / (N + 1)

확률 분포의 적합성

연속 분포

모수와 다른 누적 정규 확률 분포

누적 주파수 분포를 이산형 데이터 집합 대신 연속적인 수학 방정식으로 표시하기 위해, 누적 주파수 분포를 알려진 누적 확률 분포에 적합시키려고 시도할 수 있다.[2][3]
성공하면 알려진 방정식은 주파수 분포를 보고하기에 충분하며 데이터 표가 필요하지 않다. 또한, 이 방정식은 보간과 외삽에 도움이 된다. 단, 누적 주파수 분포를 추정하여 주의해야 한다. 이는 오류의 원인이 될 수 있기 때문이다. 한 가지 가능한 오류는 주파수 분포가 관측된 데이터의 범위를 벗어나 더 이상 선택된 확률 분포를 따르지 않는다는 것이다.

데이터 범위와 잘 일치하는 하한에서 상한까지 통합했을 때 값 1을 주는 방정식은 피팅을 위한 확률 분포로 사용할 수 있다. 사용할 수 있는 확률 분포의 표본은 확률 분포에서 찾을 수 있다.

확률 분포는 다음과 같은 몇 가지 방법으로 적합할 수 있다.[2]

  • 모멘트 방법, 최대우도 방법 및 확률 가중 모멘트의 방법을 사용하여 X 데이터의 평균 및 표준 편차와 같은 모수를 결정하는 파라메트릭 방법.
  • 회귀 분석 방법: 변환을 통해 확률 분포를 선형화하고 변환된 X 데이터에 대해 변환된 Pc의 선형 회귀(순위에서 관찰됨)로부터 매개변수를 결정한다.

예를 들어 두 가지 방법의 적용 방법

종종 여러 분포가 데이터에 잘 적합하고 유의하게 다른 결과를 산출하지 않는다는 것을 보여주지만, 이들 분포 간의 차이는 신뢰 구간의 폭에 비해 작을 수 있다.[2] 이는 어떤 분포가 더 나은 결과를 제공하는지를 결정하는 것이 어려울 수 있음을 보여준다. 예를 들어, 근사적으로 정규 분포를 따르는 데이터 세트는 많은 수의 서로 다른 확률 분포에 적합할 수 있다.[4] 부정적으로 치우친 분포는 정사각형 정규 분포와 미러링된 Gumbel 분포에 적합할 수 있다.[5]

불연속성을 갖는 누적 주파수 분포

불연속분포

때때로 데이터 범위의 하위 부분에 확률 분포의 한 유형을 적합시킬 수 있으며, 중단점에 의해 분리된 다른 유형을 상위 부분에 적합시킬 수 있으며, 이 경우 전체 적합도가 개선된다.

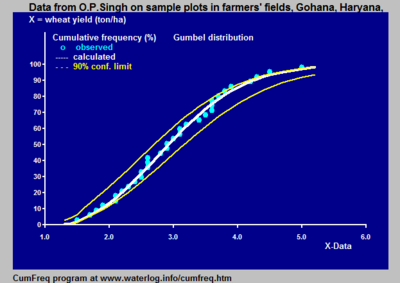
이 수치는 기후가 태평양의 전류 엘니뇨의 행동의 영향을 받는 페루 북부의 강우 데이터에 대한 그러한 불연속 분포의 유용한 예를 보여준다. 니뇨가 에콰도르 남쪽까지 뻗어 페루 연안을 따라 바다로 들어가면 페루 북부의 기후는 열대성 기후가 되고 습기가 차게 된다. 니뇨가 페루에 도달하지 못하면 기후는 반건조적이다. 이 때문에 강수량이 많을수록 적은 강우량과는 다른 주파수 분포를 따른다.[6]

예측

불확실성

데이터 기록에서 누적 빈도 분포를 도출할 때 예측에 활용할 수 있는지 의문을 제기할 수 있다.[7] 예를 들어, 1950-2000년도의 하천 방류 분포를 고려할 때, 이 분포를 사용하여 2000-50년도의 특정 하천 방류량이 얼마나 자주 초과될 것인지를 예측할 수 있는가? 환경 조건이 변하지 않는다면 대답은 그렇다. 하천 유역의 기반시설이나 기후변화에 따른 강우량 패턴의 변경 등 환경조건이 바뀌면 역사기록에 근거한 예측은 체계적 오류가 발생한다. 계통 오류가 없는 경우에도 무작위 오류가 발생할 수 있는데, 1950 - 2000년 동안 관찰된 배출량은 우연한 기회에 정상보다 높거나 낮았을 수 있는 반면, 2000 - 2050년 배출은 우연한 기회에 정상보다 낮거나 높을 수 있기 때문이다. 이것에 관한 문제들은 <검은 백조>라는 책에서 탐구되어 왔다.

신뢰구간

N = 20 크기의 표본에서 Pc = 0.1(파란색), 0.5(녹색) 및 0.8(빨간색)에 대한 이항 분포. Pc = 0.5인 경우에만 분포가 대칭임
로그 척도의 90% 이항 신뢰 벨트.

확률 이론은 랜덤 오차가 있을 수 있는 범위를 추정하는 데 도움이 될 수 있다. 누적 주파수의 경우 특정 기준 값 X를 초과하거나 초과하지 않는 두 가지 가능성만 있다. 초과 빈도와 누적 빈도의 합은 1 또는 100%이다. 따라서 이항 분포는 랜덤 오차 범위를 추정하는 데 사용할 수 있다.

정규 이론에 따르면, 이항 분포는 근사치가 가능하고 큰 N 표준 편차 Sd는 다음과 같이 계산할 수 있다.

  • Sd =sdPc(1 - Pc)/N

여기서 Pc는 누적 확률이고 N은 데이터 수입니다. 표준 편차 Sd는 증가하는 관측치 N에서 감소하는 것으로 보인다.

pc의 신뢰구간 결정은 학생의 t-테스트(t)를 이용한다. t 값은 신뢰 구간 추정치의 데이터 수와 신뢰 수준에 따라 달라진다. 그런 다음 대칭 분포에서 Pc의 신뢰 하한(L)과 상한(U)을 다음에서 찾는다.

  • L = Pc - tsdSd
  • U = Pc + t⋅Sd

이것은 월트 간격이라고 알려져 있다.[8] 그러나 이항 분포는 pc = 0.5일 때 평균을 중심으로 대칭적일 뿐 pc가 0이나 1에 가까워지면 비대칭이 되고 점점 꼬임 현상이 심해진다. 따라서 근사치에 의해 pc와 1-Pc는 t 할당에서 중량 계수로 사용될 수 있다.Sd to L 및 U:

  • L = Pc − 2⋅Pc⋅t⋅Sd
  • U = Pc + 2⋅(1−Pc)⋅t⋅Sd

여기서 Pc = 0.5에 대한 이러한 표현들이 이전 표현들과 동일하다는 것을 알 수 있다.

예
N = 25, Pc = 0.8, Sd = 0.08, 신뢰 수준은 90% t = 1.71, L = 0.58, U = 0.85
따라서 90%의 신뢰도로 0.58 < pc < 0.85>라는 것을 알 수 있다.
그래도 pc < 0.58>, 또는 pc > 0.85의 확률 10%가 있다.

메모들

  • 월드 간격은 성능이 좋지 않은 것으로 알려져 있다.[9][10][11]
  • Wilson 점수 구간은[12] 점수 테스트를 기반으로 한 이항 분포에 대한 신뢰 구간을 제공하며, 표본 범위가 더 우수하며, 자세한 개요는 이항 비율 신뢰 구간을[13] 참조하십시오.
  • 위의 가중치가 포함된 경우 "Wilson 점수 간격" 대신 "Wald interval"도 사용할 수 있다.

반환기간

주요 기사: 반환기간
반환 기간 및 신뢰 벨트. 반환 기간의 곡선은 기하급수적으로 증가한다.

누적 확률 Pc는 비초과의 확률이라고도 할 수 있다. 초과 Pe(생존 함수라고도 함)의 확률은 다음과 같다.

  • Pe = 1 − Pc

반환 기간 T는 다음과 같이 정의된다.

  • T = 1/Pe

그리고 연구에서 변수의 값이 T에 사용된 값보다 큰 것을 찾기 위해 다시 수행해야 하는 예상 관측치의 수를 나타낸다.
반환 기간의 신뢰 상한(TU) 및 하한(TL)은 다음과 같이 각각 확인할 수 있다.

  • TU = 1/(1−U)
  • TL = 1/(1−L)

연구에서 변수의 극단값의 경우 U는 1에 가깝고 U의 작은 변화는 T에U 큰 변화를 일으킨다. 따라서 극단값의 추정 반환 기간은 큰 랜덤 오차의 영향을 받는다. 또한 발견된 신뢰 구간은 장기 예측을 위해 유지된다. 더 짧은 런에서의 예측의 경우, 실제로 신뢰 구간 U-L과 T-T가UL 더 넓어질 수 있다. t-검사에 사용된 제한적 확실성(100% 미만)과 함께, 예를 들어 100년 강우량이 10년에 두 번 발생할 수 있는 이유를 설명한다.

이론적 1000년 기록(기준선)에서 50년 표본에 대한 9개의 반환 주기 곡선

반환 기간에 대한 엄격한 개념은 사실 포인트 강우처럼 시간에 의존하는 현상에 관한 경우에만 의미가 있다. 그 다음 반환 기간은 초과가 다시 발생할 때까지 예상되는 대기 시간에 해당한다. 반환 기간은 각 관측치가 대표되는 시간과 동일한 차원을 가진다. 예를 들어, 관측치가 일일 강우와 관련된 경우, 반환 기간은 일 단위로 표시되며, 연간 강우량의 경우 년 단위로 표시된다.

신뢰 벨트 필요

그림은 특정 확률 분포를 따르는 변수의 표본을 얻을 때 발생할 수 있는 변동을 보여준다. 자료는 벤슨에 의해 제공되었다.[1]

실험 누적 주파수 또는 반환 기간 곡선을 둘러싼 신뢰 벨트는 실제 분포를 찾을 수 있는 지역에 대한 인상을 준다.

또한 실험적으로 발견된 최적 적합 확률 분포가 실제 분포에서 벗어날 수 있음을 명확히 한다.

히스토그램

수정된 누적 확률 분포에서 파생된 히스토그램
로지스틱 분포에 대한 누적 확률 분포에서 파생된 히스토그램 및 확률 밀도 함수.

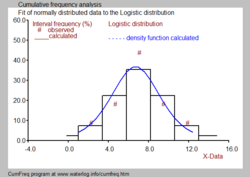
관측된 데이터는 일련번호 k를 가진 클래스 또는 그룹으로 배열할 수 있다. 각 그룹은 하한(Lk)과 상한(Uk)이 있다. 클래스(k)에 m 데이터가k 포함되어 있고 총 데이터 수가 N이면 상대 클래스 또는 그룹 주파수는 다음에서 찾을 수 있다.

  • Fgk(Lk < X ≤ Uk) = m / N

또는 간단히:

  • Fgk = m/N

또는 백분율:

  • Fg(%) = 100m/N

모든 클래스 주파수의 표시는 주파수 분포 또는 히스토그램을 제공한다. 히스토그램은 같은 기록으로 만들어졌을 때도 등급 제한에 따라 다르다.

히스토그램은 적합된 누적 확률 분포에서 파생될 수도 있다.

  • Pgk = Pc(Uk) − Pc(Lk)

적합된 분포에서 관측된 데이터의 편차로 인해 Fg와k Pgk 사이에 차이가 있을 수 있다(파란색 그림 참조).

종종 히스토그램을 흑백 그림에 묘사된 확률밀도함수와 결합하는 것이 바람직하다.

참고 항목

참조

  1. ^ a b 벤슨, M.A. 1960. 이론적 1000년 기록에 기초한 주파수 곡선의 특성. In: T. Dalrymple(편집), Flood frequency 분석. 미국 지질 조사 용수 공급 용지 1543-A, 페이지 51–71
  2. ^ a b c d 빈도 및 회귀 분석. 제6장: H.P. 리츠마(ed, 1994), 배수 원리 및 응용, Publ. 16, 페이지 175–224, 국제 토지 개간 및 개선을 위한 국제 연구소(ILRI), 네덜란드 와게닝겐. ISBN90-70754-33-9. nr. 12 아래의 웹 페이지[1]에서 무료 다운로드 또는 PDF로 직접 다운로드: [2]
  3. ^ David Vose, 데이터에 대한 적합 분포
  4. ^ 많은 수의 서로 다른 확률 분포를 적합시킬 수 있는 근사적으로 정규 분포를 따르는 데이터 집합의 예 [3]
  5. ^ 왼쪽(부정적으로) 치우친 주파수 히스토그램을 정사각형 정상 또는 미러링된 옴벨 확률 함수에 장착할 수 있다. [4]
  6. ^ CumFreq, 신뢰 대역, 반환 기간 및 불연속 옵션을 사용한 누적 주파수 분석 프로그램. 무료 다운로드: [5]
  7. ^ Silvia Masciocchi, 2012, 입자 물리학의 통계적 방법, 강의 11, 겨울 학기 2012 / 13, GSI Darmstadt. [6]
  8. ^ Wald, A.; J. Wolfowitz (1939). "Confidence limits for continuous distribution functions". The Annals of Mathematical Statistics. 10 (2): 105–118. doi:10.1214/aoms/1177732209.
  9. ^ Ghosh, B.K (1979). "A comparison of some approximate confidence intervals for the binomial parameter". Journal of the American Statistical Association. 74 (368): 894–900. doi:10.1080/01621459.1979.10481051.
  10. ^ Blyth, C.R.; H.A. Still (1983). "Binomial confidence intervals". Journal of the American Statistical Association. 78 (381): 108–116. doi:10.1080/01621459.1983.10477938.
  11. ^ Agresti, A.; B. Caffo (2000). "Simple and effective confidence intervals for pro- portions and differences of proportions result from adding two successes and two failures". The American Statistician. 54 (4): 280–288. doi:10.1080/00031305.2000.10474560. S2CID 18880883.
  12. ^ Wilson, E.B. (1927). "Probable inference, the law of succession, and statistical inference". Journal of the American Statistical Association. 22 (158): 209–212. doi:10.1080/01621459.1927.10502953.
  13. ^ Hogg, R.V. (2001). Probability and statistical inference (6th ed.). Prentice Hall, NJ: Upper Saddle River.