수치적 통합

미분 방정식
장애물 주위의 공기 흐름을 시뮬레이션하는 데 사용되는 Navier-Stokes 미분 방정식
범위
보여 주다 필드 자연과학 공학 천문학 물리학 화학 생물학 지질학 응용 수학 연속체 역학 혼돈 이론 다이너믹 시스템 사회과학 경제학 인구역학
분류
보여 주다 종류들 보통 부분적 차동알지브라질 인터그로 차동 분수 선형 비선형 변수 유형별 종속변수와 독립변수 자율적 콤플렉스 결합/분리됨 정확한 동종/비동종 특징들 주문 연산자 표기법
보여 주다 프로세스와의 관계 차이(구체 아날로그) 스토카스틱 확률적 부분 지연
해결책
보여 주다 존재와 고유성 피카르-린델뢰프 정리 페아노 존재 정리 카라테오도리의 존재 정리 카우치-코왈레프스키 정리
보여 주다 일반 주제 룬스키안 위상 초상화 위상공간 랴푸노프 / 점근증 / 지수 안정성 수렴율 시리즈/적분 솔루션 수치적 통합 디라크 델타 함수
보여 주다 솔루션 방법 감사 특성방법 오일러 지수 반응식 유한차이 (크랭크-니콜슨) 유한요소 무한요소 유한 부피 갤러킨 페트로프-갈러킨 집적인자 적분 변환 섭동 이론 룬게쿠타 변수의 분리 결정되지 않은 계수 모수의 변동
사람
보여 주다 리스트 아이작 뉴턴 고트프리드 라이프니즈 레온하르트 오일러 에밀 피카르 요제프 마리아 회네브로이스키 에른스트 린델뢰프 루돌프 립시츠 아우구스틴루이코치 존 크랭크 필리스 니콜슨 칼 데이비드 톨메 룬지 마르틴 쿠타
v t

수치적 통합은 $값{\displaystyle }$ S$${\$displaystyle S}$에 대한 수치 근사치 계산에 사용된다$,$ $f{\displaystyle }$( ${\displaystyle x}$) ${\displaystyle f(x)}$에 의해 정의된 곡선 아래의 영역.

분석에서 수치적 통합은 확정적분량의 수치적 가치를 계산하기 위한 광범위한 알고리즘 계열로 구성되며, 확장적으로 미분 방정식의 수치적 해답을 설명하는 데에도 이 용어가 사용되기도 한다. 이 글은 명확한 통합의 계산에 초점을 맞추고 있다.

숫자 4각형(흔히 4각형으로 약칭)이라는 용어는 특히 1차원 통합에 적용되는 수치 통합의 동의어에 가깝다. 어떤 저자는 둘 이상의 차원에 걸친 수치적 통합을 입체이라고 하며,^[1] 다른 저자는 고차원적 통합을 포함하기 위해 사분법을 사용한다.

수치 통합의 기본적인 문제는 명확한 적분들에 대한 대략적인 해결책을 계산하는 것이다.

${\displaystyle \int _{a}^{b}f(x)\,dx}$

어느 정도 정확하게 f(x)가 소수의 차원에 걸쳐 통합된 매끄러운 함수이고, 통합의 영역이 경계인 경우, 원하는 정밀도에 대한 적분량을 근사하는 방법은 많다.

수치적 통합의 이유

해독제를 찾아 분석적 통합과 달리 수치적 통합을 수행하는 데는 다음과 같은 몇 가지 이유가 있다.

1. 통합형 및 f(x)는 샘플링을 통해 얻은 것과 같은 특정 지점에서만 알 수 있다. 일부 임베디드 시스템과 다른 컴퓨터 애플리케이션은 이러한 이유로 수치적 통합이 필요할 수 있다.
2. 통합의 공식은 알 수 있지만, 기본적인 기능인 해독제를 찾기가 어렵거나 불가능할 수 있다. 그러한 통합의 예로는 f(x) = exp(-x²)가 있는데, 그 반분법(오류 함수, 곱하기 상수)은 기초적인 형태로 작성할 수 없다.
   참고 항목: 비원소 적분
3. 상징적으로 해독제를 찾는 것이 가능할 수도 있지만, 해독제를 계산하는 것보다 수치 근사치를 계산하는 것이 더 쉬울 수도 있다. 항변제를 무한 시리즈나 제품으로 주거나, 그 평가에서 사용할 수 없는 특수한 기능이 필요한 경우일 수 있다.

역사

"수리적 통합"이라는 용어는 데이비드 깁의 "수학적 연구소를 위한 보간 및 수치적 통합 과정"이라는 간행물에서 1915년에 처음 나타난다.^[2]

사분법은 영역 계산이라는 뜻의 역사적 수학적 용어다. 4차적 문제는 수학적 분석의 주요 원천 중 하나로 작용해 왔다. 고대 그리스의 수학자들은 피타고라스 교리에 따르면 면적 계산을 기하학적으로 같은 면적(스퀴링)을 가진 정사각형을 건설하는 과정으로 이해했다. 그것이 이 과정이 4가지로 명명된 이유다. 예를 들어, 원의 4각형, 히포크라테스의 룬, 파라볼라의 4각형. 이 건축은 나침반과 직선으로만 수행되어야 한다.

고대 바빌로니아인들은 사다리꼴 규칙을 사용하여 황색계를 따라 목성의 운동을 통합했다.^[3]

기하학적 평균을 찾는 앤티크 방법

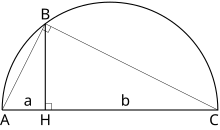
면 a와 b가 있는 직사각형의 4각형의 경우 $측면{\displaystyle }$ x${\displaystyle }$= ${\displaystyle \sqrt{b}}$ ${\$a와 b의 기하학적 평균)로 정사각형을 구성해야 한다. 이를 위해 a와 b의 합을 지름으로 하여 원을 그리면 높이 BH(그들이 연결된 지점에서 원과 교차하는 지점까지)가 기하학적 평균과 같다는 사실을 사용할 수 있다. 유사한 기하학적 구조는 평행사변형과 삼각형을 위한 4각형의 문제를 해결한다.

포물선의 세그먼트 영역

곡선형의 경우 4각형의 문제가 훨씬 더 어렵다. 나침반과 직선자를 가진 원의 4각형은 19세기에 불가능하다는 것이 증명되었다. 그럼에도 불구하고 일부 수치(예: 히포크라테스의 룬)의 경우 사분법을 수행할 수 있다. 아르키메데스가 수행한 구체 표면과 포물선 부분의 4각형은 골동품 분석의 가장 높은 성취가 되었다.

• 구의 표면적은 이 구의 큰 원의 면적을 4배로 하는 것과 같다.
• 포물선을 직선으로 자른 포물선 부분의 면적은 이 세그먼트에 새겨진 삼각형의 면적의 4/3이다.

그 결과의 증거를 위해 아르키메데스는 에우독소스의 소진법을 사용하였다.

중세 유럽에서는 4각형이 어떤 방법으로든 면적을 계산하는 것을 의미했다. 더 자주 불분명한 방법들이 사용되었다; 그것은 덜 엄격했지만 더 단순하고 강력했다. 갈릴레오 갈릴레이와 길레스 드 로베르발은 사이클로이드 아치의 면적을 찾아냈으며, 그레고아르 드 생 빈센트는 하이퍼볼라(Opus Giomicalum, 1647), 알폰스 안토니오 데 사라사 데 생 빈센트의 제자 및 해설자로 이 면적의 로그와의 관계에 주목했다.

존 월리스 알헤지는 이런 방법을 고안해 냈다: 그는 산술적으로 인피니토리움 (1656) 시리즈에서 우리가 이제 확정 적분이라고 부르는 것을 썼고, 그들의 가치를 계산했다. Isaac Barrow와 James Gregory는 더 발전했다: 몇몇 대수학적 곡선과 나선형들을 위한 4각형. Christiaan Huygens는 성공적으로 혁명의 고형물을 4중으로 만들었다.

생빈센트와 데 사라사의 하이퍼볼라의 4각은 매우 중요한 새로운 기능인 자연 로그(natural logarithm)를 제공했다.

적분 미적분학의 발명과 함께 면적 계산을 위한 보편적인 방법이 나왔다. 이에 4각형이라는 용어는 전통적이 되었고, 그 대신 현대적인 구절인 "일변량 확정 적분 계산"이 더 흔하다.

1차원 통합 방법

수치적 통합 방법은 일반적으로 통합에 대한 평가를 결합하고 통합에 대한 근사치를 얻는 것으로 설명할 수 있다. 적분량은 적분점이라고 불리는 유한한 점 집합에서 평가되며, 이러한 값의 가중 합계는 적분량의 근사치를 위해 사용된다. 통합 지점과 가중치는 사용된 특정 방법과 근사치에서 요구되는 정확도에 따라 달라진다.

수치 통합 방법의 분석에서 중요한 부분은 통합 및 평가 횟수의 함수로서 근사 오차의 동작을 연구하는 것이다. 소수의 평가에서 작은 오차를 내는 방법은 대개 우월한 것으로 간주된다. 통합에 대한 평가 횟수를 줄이고 관련된 산술 연산의 횟수를 줄임으로써 전체 반올림 오차를 줄인다. 또한, 각각의 평가는 시간이 걸리고, 통합은 임의로 복잡할 수 있다.

통합이 합리적으로 잘 되어 있는 경우(즉, 조각처럼 연속적이고 경계가 있는 변동) 통합은 매우 작은 증분으로 통합성을 평가함으로써 수행될 수 있다.

보간 기능에 따른 2차 규칙

통합이 용이한 보간 기능을 구성하면 대종류의 4차 규칙을 도출할 수 있다. 전형적으로 이러한 보간함수는 다항식이다. 실제로 매우 높은 수준의 다항식들은 마구 진동하는 경향이 있기 때문에 일반적으로 선형과 2차적인 저도의 다항식만 사용된다.

사각형 규칙의 그림.

이러한 유형의 가장 간단한 방법은 보간 기능을 점$\frac{(+b}{}$ $\frac{\mathrm{}}{}$,$f$ $\frac{(+}{\mathrm{}}$ 2$){\$frac {a+b}{2}{\$frac {a+b$}{\b}{\frac {a+b$}{2$}{2)를 통과하는 상수 함수(도 0의 다항식)가 되도록 하는 것이다.$}}\오른쪽)\오른쪽$ 이를 중간점 규칙 또는 직사각형 규칙이라고 한다.

${\displaystyle \int _{a}^{b}f(x)\,dx\trawth (b-a)f\left\frac {a+b}{2}}\오른쪽).}$

사다리꼴 규칙의 그림.

보간 함수는 점$({\displaystyle a}$,${\displaystyle f}$( ) ${\$${\displaystyle }$및$$ $,$)\right$)}$을 통과하는 직선(즉, appine 함수)일 수 있다$.$ 이것을 사다리꼴 법칙이라고 한다.

${\displaystyle \int_{a}^{b}f(x)\,dx\trawth (b-a)\left\fract\frac {f(a)+f(b)}{2}}\오른쪽).}$

심슨의 법칙의 삽화.

이러한 규칙들 중 하나에 대해, ${\displaystyle \mathrm{우리}}$는 구간${\displaystyle }$[${\displaystyle }$a , ${\displaystyle b}$ ${\displaystyle ]}$ ${\displaystyle [a,b]}$을(를) 하위절차의 $일부$ n ${\displaystyle n}($으)로$$ 세분화하여 각 하위절차에 대한 근사치를 계산한 다음, 모든 결과를 합산하여 보다 정확한 근사치를 만들 수 있다. 이를 복합 규칙, 확장 규칙 또는 반복 규칙이라고 한다. 예를 들어 복합 사다리꼴 규칙은 다음과 같이 말할 수 있다.

${\displaystyle \int _{a}^{b}f(x)\,dx\approx {\frac {b-a}{n}}\left({f(a) \over 2}+\sum _{k=1}^{n-1}\left(f\left(a+k{\frac {b-a}{n}}\right)\right)+{f(b) \over 2}\right),}$

where the subintervals have the form ${\displaystyle [a+kh,a+(k+1)h]\subset [a,b],}$ with ${\textstyle h={\frac {b-a}{n}}}$ and ${\displaystyle k=0,\ldots ,n-1.}$ Here we used subintervals of the same length ${\displaystyle h}$ but one could also 다양한 ${\displaystyle {}_{}}$의 간격$({\displaystyle {{}_{}}_{}}$ ${\displaystyle {k_{}}_{}}$) k ${\$ 사용$_{k}}$.

$[{\displaystyle }$ ${\displaystyle a}$, ${\displaystyle b}$ ${\displaystyle ]}$ ${\displaystyle [a,b]}$의 동일한 간격의 점에서 평가된 다항식과의 보간에서는 뉴턴-코테스 공식을$$ 산출하며, 그 중 사각형 규칙과 사다리꼴 규칙이 예시된다. 순서 2의 다항식을 바탕으로 한 심슨의 법칙도 뉴턴-코테스 공식이다.

동일한 간격의 점을 갖는 사분법 규칙은 내포라는 매우 편리한 특성을 가지고 있다. 각 구간을 세분화한 해당 규칙에는 모든 현재 지점이 포함되므로 이러한 통합 및 값을 다시 사용할 수 있다.

보간점 사이의 간격을 변경하도록 허용하면 가우스 4차 공식과 같은 다른 4차 공식 그룹을 찾을 수 있다. 가우스 사분법 규칙은 일반적으로 뉴턴-코테스 규칙보다 더 정확하며, 이 규칙에서는 통합과 통합이 원활하다면(즉, 충분히 다를 수 있는 경우) 동일한 수의 기능 평가가 동일해야 한다. 구간이 다양한 다른 4각형 방법으로는 중첩을 하는 Clenshaw-Curtis 4각형(Fejér 4각형이라고도 함) 방법이 있다.

가우스 사분법 규칙은 내포하지 않지만 관련 가우스-크론로드 사분법 공식은 내포한다.

일반화 중간점 규칙 공식

일반화된 중간점 규칙 공식은 다음과 같다.

${\displaystyle \int _{0}^{1}{f(x)\,dx}=\sum _{m=1}^{M}{\sum _{n=0}^{\infty }{{\frac {\left({-1}\right)^{n}+1}{{\left(2M\right)^{n+1}}\left({n+1}\right)!}}{{{\왼쪽.f^{(n)}(x)\오른쪽 }_{x={\frac{m-1/2}}:}}}}}}$

또는

${\displaystyle \int _{0}^{1}{f(x)\,dx}=\lim _{M\to \infty }\sum _{m=1}^{M}{\sum _{n=0}^{N}{{\frac {\left({-1}\right)^{n}+1}{{{\left({2M}\right)}^{n+1}}\left({n+1}\right)!}}{{\left.f^{(n)}(x)\오른쪽 _{x={\frac{m-1/2}}:}}},}$

여기서 $f{\displaystyle {}^{}}$( ${\displaystyle n{}^{}}$)${\displaystyle {}^{}}$( x${\displaystyle }$) ${\displaystyle$ f$^{(n)}(x)}$은 $n{\displaystyle }$ ${\displaystyle n}$ -th 파생상품을 의미한다$$. 예를$$ 들어 $대체{\displaystyle \mathrm{M}}$ = 1 ${\displaystyle M=1$} 및

${\displaystyle f(x)={\frac {\theta }{1+\theta ^{2}x^{2}}:$

일반화된 중간점 규칙 공식에서 역 탄젠트의 방정식을 구한다.

${\displaystyle \tan ^{-1}(\theta )=i\sum _{n=1}^{\infty }{\frac {1}{2n-1}}\left({\frac {1}{\left(1+2i/\theta \right)^{2n-1}}}-{\frac {1}{\left(1-2i/\theta \right)^{2n-1}}}\right)=2\sum _{n=1}^{\infty }{{\frac {1}{2n-1}}{\frac {a_{n}\left(\theta \right)}}{a_{n}^{2}\왼쪽(\theta \right)+b_{n}^{2}\left(\theta \right)}}}}}},$

여기서 $i{\displaystyle }$=${\displaystyle \sqrt{}}$- ${\displaystyle \sqrt{1}}$ ${\$ i$={\sqrt{-1}}$은(는) 가상 단위이며

${\displaystyle {\begin{aligned}a_{1}(\theta )&={\frac {2}{\theta }},\\b_{1}(\theta )&=1,\\a_{n}(\theta )&=\left(1-{\frac {4}{\theta ^{2}}}\right)\,a_{n-1}(\theta )+{\frac {4}{\theta }}\,b_{n-1}(\theta ),\\b_{n}(\theta )&=\left(1-{\frac {4}{\theta ^{2}}}\right)\,b_{n-1}(\theta )-{\frac {4}{\theta }}\,a_{n-1}(\theta ).\end{정렬}}}$

각 홀수 $n{\displaystyle }$ ${\displaystyle n}$에서 통합의 분자가${\displaystyle }$(${\displaystyle }$- ${\displaystyle 1{}^{}}$) n${\displaystyle {}^{}}$+ ${\displaystyle 1}$= ${\displaystyle 0}$ ${\displaystyle(-1)^{n}+1=0}$이 되기 때문에 일반화된 중간점 규칙 공식은 다음과 같이 재구성할 수 있다$.$

${\displaystyle \int_{0}^{0}^{f(x)\,dx}=2\sum _{m=1}^{n=0}^{n=0}^{\frac {1}{{\frac {1}{{\n+1}:{2n+1}:{2}}}\오른쪽!}}{{{\좌측.f^{{n)}(x)\오른쪽 }_{x={\frac{m-1/2}}:}}},\,}$

다음 Mathematica 코드의 예는 $M{\displaystyle }$= ${\displaystyle 5}$ ${\displaystyle M=5}$ 및 $N$ = ${\displaystyle 10}$ ${\displaystyle N=10}$에서 잘린 근사치와 역 접선 사이의 차이를 보여주는 그래프를 생성한다$.$

f[세타, x_] := 세타/(1 + 세타^2 * x^2);  aTan[세타, M_, nMax_] :=      2*합계[(함수[x, 평가하다[D[f[세타, x], {x, 2*n}]]][(m - 1/2)/         M])/((2*n + 1)!*(2*M)^(2*n + 1)), {m, 1, M}, {n, 0, 엔맥스}];  플롯[{아크탄[세타] - aTan[세타, 5, 10]}, {세타, -파이, 파이},   플롯 범위 -> 전부] 

간격$({\displaystyle }$${\displaystyle ,}$${\displaystyle b}$)에 걸쳐 정의된$$ 함수 g$(t$ ) {\$displaystyle$ g$(t)}$의 경우$,$ 그 $적분은$

${\displaystyle \int_{a}^{b}{g(t)\,dt}=\int_{0}^{b-a}{g(\tau +a)\,d\nt_{0}^{g(b-a)x+a)\,dx}}$

따라서 $f{\displaystyle }$( ${\displaystyle x}$)${\displaystyle }$=${\displaystyle }$( b${\displaystyle }$- ${\displaystyle a}$) g${\displaystyle }$(${\displaystyle }$( ${\displaystyle b}$- ${\displaystyle a}$) ${\displaystyle x}$+ a${\displaystyle }$) ${\displaystyle f(x)=(b-a)\,g(b-a)x+a)}$을 가정하여 위의 일반화된 중간점 통합 공식을 적용할 수 있다$.$

적응 알고리즘

f(x)에 모든 점에서 많은 파생상품이 없거나 파생상품이 커지면 가우스 사분법이 부족한 경우가 많다. 이 경우 다음과 유사한 알고리즘이 더 좋은 성능을 발휘하게 된다.

반항하다 calculate_credit_of_f(f, initial_step_size):     """     이 알고리즘은 함수의 확정 적분을 계산한다.     0에서 1까지, 적응적으로, 근처의 더 작은 단계를 선택함     문제점     """     x = 0.0     h = initial_step_size     축전지 = 0.0     하는 동안에 x < 1.0:         만일 x + h > 1.0:             h = 1.0 - x  # 단위 간격이 끝나면 마지막 단계를 1에서 끝까지 조정한다.         만일 error_too_big_in_in_virature_of_f_over_range(f, [x, x + h]):             h = make_h_make(h)         다른:             축전지 += 4배수_of_f_over_range(f, [x, x + h])             x += h             만일 error_too_small_in_in_virature_of_over_range(f, [x, x + h]):                 h = make_h_make(h)  # 작은 발걸음으로 시간을 낭비하지 마라.     돌아오다 축전지 

알고리즘의 일부 세부사항에는 신중한 생각이 필요하다. 많은 경우, 함수 f(x)에 대한 간격에 대한 4각형의 오차를 추정하는 것은 명확하지 않다. 한 가지 일반적인 해결책은 두 가지 서로 다른 사분법 규칙을 사용하고, 그 차이를 사분법에서 오차의 추정치로 사용하는 것이다. 또 다른 문제는 "너무 큰" 혹은 "아주 작은"이 무엇을 의미하는지 결정하는 것이다. "너무 큰"의 로컬 기준은 4차 오차가 t ⋅ h보다 커서는 안 된다는 것이다. 여기서 t는 실제 수치로서 글로벌 오차에 대해 설정하고자 하는 허용오차이다. 한편, h가 이미 작다면, 사분오차가 명백하게 크더라도 그것을 더 작게 만드는 것은 가치가 없을지도 모른다. 글로벌 기준은 모든 구간에 대한 오차 합계가 t보다 작아야 한다는 것이다. 이러한 유형의 오류 분석은 근사치를 계산한 후 오류를 계산하기 때문에 보통 "후사"라고 불린다.

적응형 사분면에 대한 휴리스틱스는 Foristhe 등(제5.4절)에서 논한다.

외삽법

뉴턴-코트 유형의 4각 규칙의 정확도는 일반적으로 평가 지점 수의 함수다. 결과는 일반적으로 평가점수가 증가할수록 더 정확하며, 또는 점 사이의 단계크기의 폭이 감소할 때 동등하게 나타난다. 스텝 크기가 0에 근접하도록 허용하면 어떤 결과가 나올지 묻는 것은 당연하다. 이는 리차드슨 외삽과 같은 시리즈 가속 방법을 사용하여 0이 아닌 두 개 이상의 스텝 크기에서 결과를 추정함으로써 대답할 수 있다. 외삽 함수는 다항식 또는 합리적인 함수일 수 있다. 외삽법은 스토어(Stoer)와 벌러슈(제3.4)에 의해 보다 상세하게 설명되며, 쿼드팩 라이브러리의 많은 루틴에서 구현된다.

보수적(priori) 오차 추정

$f{\displaystyle }$ ${\displaystyle f}$이$({\displaystyle 가}$) ${\displaystyle [,}$ ${\displaystyle b}$ ${\displaystyle ]}$, ${\displaystyle [a,b],},$ 예$$: $f{\displaystyle }$ ${\displaystyle \in }$ ${\displaystyle {C\mathrm{}}^{}}$ $1$ ${\displaystyle a,}$ ${\displaystyle b}$ ${\displaystyle ]}$ )${\displaystyle }$. ${\displaystyle f\in{1}([,b])$에 대해 경계된 첫 번째 파생상품을 갖도록$$ 한다.$}$ $f{\displaystyle }$, ${\displaystyle f,}$에 대한 평균 값 정리. 여기서$$ $x{\displaystyle }$ ${\displaystyle \in [,}$ ${\displaystyle b}$ ${\displaystyle x\in$ [$a,b$]은 다음과$$같다$$.

${\displaystyle (x-a)f'(\xi _{x}=f(x)-f(a),}$

$x{\displaystyle }$ ${\displaystyle$ x$}$에 따라$$ 일부 $\xi {\displaystyle {}_{}}$ ${\displaystyle x_{}](,}$ ${\displaystyle x}$] {\$displaystyle \xi _{x}\in(a,x$])의 경우$.$

$만약{\displaystyle }$ 우리가 양쪽의$$ ${\displaystyle a}$에서 $b{\displaystyle }$ ${\displaystyle b}$까지 x ${\displaystyle x}$로 통합하고 절대값을 취한다면, 우리는 얻을 수 있다.

${\displaystyle \왼쪽 \int _{a}^{b}f(x)\,dx-(b-a)f(a)\right \int _{a}^{b}(x-a)f'(\xi _{x})\,dx\right.}$

또한 절대값을 통합으로 가져오고 $f{\displaystyle {}^{}}$ ${\displaystyle {\prime }^{}}${\$displaystyle f'}$의 용어를 상한으로$$ 대체함으로써 우측에 있는 적분을 더 자세히 추정할 수 있다.

${\displaystyle \left \int _{a}^{b}f(x)\,dx-(b-a)f(a)\right \leq {(b-a)^{2} \over 2}\sup _{a\leq x\leq b}\leq(x)\right ,}$

(1)

그 우월감이 근사하게 사용된 곳이지

따라서 2차 규칙$({\displaystyle b}$- ${\displaystyle a}$ )$$f ($x$) d $x$ $(\textstyle \int _{a}^{b($$x)\,dx$$}$을$(를)$ 4차 규칙(b - a${\displaystyle )}$으로 추정하면, 우리의$$ 오차는 1의 오른손보다 크지 않다. 이것을 리만 합에 대한 오류 분석으로 변환하여 상한을 부여할 수 있다.

${\displaystyle {\frac{n^{-1}{2}}\sup _{0\leq x\leq 1}\왼쪽 f'(x)\오른쪽 }$

특정 근사치의 오차항. (${\displaystyle \mathrm{이것}}$은 정확히 $우리$가 예 f${\displaystyle }$(${\displaystyle x}$ ) = x $(\displaystyle f($x)=$x}$에 대해 계산한 오류라는 점에 유의한다.)$$ 더 많은 파생상품을 사용하며, 사분법을 수정함으로써 f에 대해 테일러 시리즈(남은 기간의 부분합 사용)를 사용하여 유사한 오류 분석을 할 수 있다. 이 오류 분석은 f의 파생상품을 이용할 수 있는 경우 오류에 엄격한 상한을 부여한다.

이 통합 방법은 컴퓨터 증명과 검증된 계산을 만들기 위해 구간 산술과 결합할 수 있다.

무한 간격에 걸친 통합

무한 간격에 걸쳐 근사적으로 통합할 수 있는 몇 가지 방법이 존재한다. 표준 기법에는 전체 실선의 통합에 대한 Gauss-Hermite 4차, 양성 실체의 통합에 대한 Gauss-Laguere 4차 등 특별히 파생된 4차 규칙이 포함된다.^[4] 몬테카를로 방법 또한 사용될 수 있다. 또는 한정된 간격으로 변수를 변경할 수 있다. 예를 들어, 전체 라인에 대해 사용할 수 있다.

${\displaystyle \int _{-\nf(x)\,dx=\int _{-1}^{+1}f+1}{+1}f\frac {t^{1-t^{2}}\오른쪽){\frac {1+t^{2}{1+t^{2}{2}}}}{{\{-t^{2}\오른쪽)^{2}}\,dt,}$

그리고 반무한 간격의 경우 사용할 수 있다.

${\displaystyle {\begin{aligned}\int _{a}^{\infty }f(x)\,dx&=\int _{0}^{1}f\left(a+{\frac {t}{1-t}}\right){\frac {dt}{(1-t)^{2}}},\\\int _{-\infty }^{a}f(x)\,dx&=\int _{0}^{1}f\left(a-{\frac {1-t}{t}}\right){\frac {dt}{t^{2}}},\end{aligned}}}$

변형 가능한 한

다차원적 통합

지금까지 논의된 4차원의 규칙은 모두 1차원 통합을 계산하도록 설계되었다. 다차원적 통합을 계산하기 위해서는 푸비니의 정리(텐서적 제품 규칙)를 적용하여 복수의 적분을 반복적인 1차원 적분으로 구문하는 것이 하나의 접근법이다. 이 접근방식은 차원 수가 증가함에 따라 기능 평가가 기하급수적으로 증가하도록 요구한다. 소위 차원성의 저주를 극복하기 위한 세 가지 방법이 알려져 있다.

다양한 가중치 기능을 위한 다차원 입체 통합 규칙을 형성하기 위한 많은 추가 기법이 스트라우드에 의해 단자 형태로 제공된다.^[5] 구체에 대한 통합은 헤세 외(2015년)에 의해 검토되었다.^[6]

몬테카를로

몬테카를로 방식과 준몬테카를로 방식은 다차원 통합에 적용하기 쉽다. 그것들은 1차원 방법을 사용한 반복적인 통합보다 동일한 수의 기능 평가에 더 큰 정확도를 산출할 수 있다.^{[citation needed]}

유용한 몬테카를로 방법의 많은 종류는 소위 마르코프 체인 몬테카를로 알고리즘으로 메트로폴리스-헤이스팅스 알고리즘과 깁스 샘플링을 포함한다.

희소 격자

희소성 그리드는 원래 스몰랴크가 고차원 함수의 사분법을 위해 개발했다. 이 방법은 항상 1차원 사분법 규칙에 기초하지만, 일변량 결과의 보다 정교한 조합을 수행한다. 그러나 텐서 제품 규칙은 4각 점의 무게가 양이면 모든 입체 점의 가중치가 양성이 된다는 것을 보장하지만, 스몰랴크의 규칙은 가중치가 모두 양성이라는 것을 보장하지는 않는다.

베이시안 쿼드라이처

베이지안 4차원은 계산 통합의 수치 문제에 대한 통계적 접근법이며 확률론적 숫자 영역에 속한다. 가우스 공정 후방 분산으로 표현된 적분 용액에 대한 불확실성의 완전한 처리를 제공할 수 있다.

미분방정식 연결

적분 평가의 문제

${\displaystyle F(x)=\int _{a}^{x}f(u)\,du}$

미적분학의 기본 정리의 첫 부분을 적용함으로써 일반적인 미분 방정식의 초기값 문제로 축소될 수 있다. x라는 인수에 관해서 위의 양쪽을 구별함으로써 F라는 함수가 만족하는 것으로 보인다.

${\displaystyle {\frac {dF(x)}{dx}=f(x),\quad F(a)=0.}$

Runge-Kutta 방법과 같은 일반적인 미분방정식을 위해 개발된 방법들은 재작성된 문제에 적용될 수 있으며 따라서 적분을 평가하는 데 사용될 수 있다. 예를 들어, 미분 방정식에 적용된 표준 4차 룬게-쿠타 방법은 위에서부터 심슨의 규칙을 산출한다.

미분 방정식 $F{\displaystyle {}^{}}$ ${\displaystyle {\prime }^{}}$( ${\displaystyle x}$)${\displaystyle }$= ${\displaystyle f}$( ${\displaystyle x}$) ${\displaystyle$ F$'(x)=f(x)}$은 특수 형태를 가지고$$ 있는데, 오른쪽에는 종속 변수가 아닌 독립 $변수{\displaystyle }$(여기$$x {\$displaystyle$ x$\})$만 포함되어 있다(여기 $F{\displaystyle }$ ${\displaystyty$ F$}).$ 이것은 이론과 알고리즘을 상당히 단순화시킨다. 따라서 통합을 평가하는 문제는 그 자체로 가장 잘 연구된다.

참고 항목

• 일반 미분방정식의 수치적 방법
• 잘라내기 오류(숫자 통합)
• 클렌쇼-커티스 사분법
• 가우스크로드 사분법
• 리만 합 또는 리만 적분
• 사다리꼴 법칙
• 롬버그의 방법
• 탄신 사분법
• 비원소 적분

참조

• 필립 J. 데이비스와 필립 라비노위츠, 수치적 통합의 방법.
• 조지 E. 포사이스, 마이클 A. 말콤, 그리고 클레브 B. 몰러, 수학적 계산을 위한 컴퓨터 방법. 엥글우드 절벽, NJ: 프렌티스 홀, 1977. (5장 참조)
• Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. (2007), "Chapter 4. Integration of Functions", Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8
• Josef Stoer와 Roland Bulirsch, 수치해석 소개. 뉴욕: Springer-Verlag, 1980. (3장 참조)
• Boyer, C. B. A 수학사, Uta C의 2차 개정판. 뉴욕 머즈바흐: 와일리, 1989 ISBN 0-471-09763-2(1991 pbk ed) ISBN 0-471-54397-7).
• Eves, Howard, 수학사 소개, Sunders, 1990, ISBN 0-03-029558-0,

외부 링크

위키미디어 커먼즈에는 수치 통합과 관련된 미디어가 있다.

• 통합: 총체적 수치법 연구소의 배경, 시뮬레이션 등
• 울프램 수학월드의 로바토 4중주곡
• 수학 백과사전의 로바토 4각형 공식
• 무료 Tracker 구성 요소 라이브러리 내에 많은 4각형 및 입체형 공식 구현.