연속 확률 분포
확률 이론 과 통계 에서 비대칭 라플라스 분포(ALD) 는 라플라스 분포 의 일반화인 연속 확률 분포 다.라플라스 분포가 x = m 에 대해 연속적으로 동일한 척도의 두 지수 분포 로 구성되는 것처럼 비대칭 라플라스 분포는 연속성과 정규화를 보장하기 위해 조정 된 x = m 에 대해 연속적으로 동일한 척도의 두 지수 분포로 구성된다. 서로 다른 평균과 비율 매개변수로 기하급수적으로 분포 하는 두 변수의 차이는 ALD에 따라 분배될 것이다. 두 비율 모수가 같을 때, 차이는 라플라스 분포에 따라 분배될 것이다. null
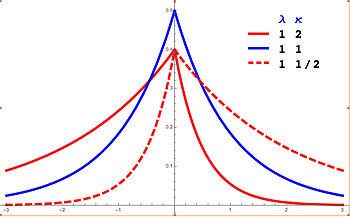
특성화 확률밀도함수 랜덤 변수는 확률밀도함수 가 다음과 같은[1] [2] m , λ , κ ) 분포를 가진다.
f ( x ; m , λ , κ ) = ( λ κ + 1 / κ ) e − ( x − m ) λ s κ s {\displaystyle f(x;m,\butda ,\kappa )=\좌측da\frace\prace{}{\cappa +1/\cappa }\, e^{-(x-m)\capa \{s}}}} 여기 서 s=sgn (x-m) 또는 다른 방법:
f ( x ; m , λ , κ ) = λ κ + 1 / κ { 생략하다 ( ( λ / κ ) ( x − m ) ) 만일 x < m 생략하다 ( − λ κ ( x − m ) ) 만일 x ≥ m {\displaystyle f(x;m,\lambda ,\kappa )={\frac {\lambda }{\kappa +1/\kappa }}{\begin{cases}\exp \left((\lambda /\kappa )(x-m)\right)&{\text{if }}x<m\\[4pt]\exp(-\lambda \kappa (x-m)) &{\text{if }x\geq m\end{case}} 여기서 m 은 위치 매개변수 , λ > 0은 척도 매개변수 , κ 은 비대칭 매개변수다. κ = 1, (x-m)s κ 이s x-m 으로 단순화되면 분포는 라플라스 분포로 단순화된다.null
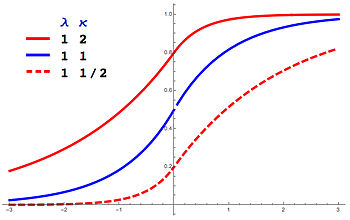
누적분포함수 누적분포함수 는 다음과 같다.
F ( x ; m , λ , κ ) = { κ 2 1 + κ 2 생략하다 ( ( λ / κ ) ( x − m ) ) 만일 x ≤ m 1 − 1 1 + κ 2 생략하다 ( − λ κ ( x − m ) ) 만일 x > m {\displaystyle F(x;m,\lambda ,\kappa )={\begin{case}{\frac {\cappa ^{2}}:{1+\kappa ^{2}}: exp(\lambda /\capa )(x-m) &{\text{{}x\leq m\\[4pt]1-{1}{1+\kappa ^{2}}:\expa\cappa (x-m) &{\text{{if}x}m\end{case}} 특성함수 ALD 특성 함수는 다음을 통해 제공된다.
φ ( t ; m , λ , κ ) = e i m t ( 1 + i t κ λ ) ( 1 − i t κ λ ) {\displaystyle \varphi (t;m,\basda,\kappa )={\frac {e^{imt}{{{1+{\frac {it\kappa }}}}}}{\fraca \cappa }}}}}}}}}}}}}}}}}} m = 0의 경우 ALD는 α = 2를 갖는 기하학적 안정 분포 계열의 구성원이다.따라서 φ 1 {\ displaystyle \varphi _{1 φ {\ displaystyle \varphi _{2 m = 0으로 구별되는 ALD 특성 함수라면 다음과 같다.
φ = 1 1 / φ 1 + 1 / φ 2 − 1 {\displaystyle \varphi ={\frac {1}{1/\varphi _{1}+1/\varphi _{2}-1} 위치 매개변수 0 {\displaystyle m=0} . 새로운 척도 매개변수 λ 준수
1 λ 2 = 1 λ 1 2 + 1 λ 2 2 {\displaystyle {\frac {1}{\fractda ^{2}}={\frac {1}{1}{1}^{1}2}}+{\fracta _{1}{2}^{2}}:} 그리고 새로운 왜도 매개변수 κ 오바이스:
κ 2 − 1 κ λ = κ 1 2 − 1 κ 1 λ 1 + κ 2 2 − 1 κ 2 λ 2 {\displaystyle {\frac {\kappa ^{2}-1}{\kappa \lambda }}={\frac {\kappa _{1}^{2}-1}{\kappa _{1}\lambda _{1}}}+{\frac {\kappa _{2}^{2}-1}{\kappa _{2}\lambda _{2}}}} 모멘트, 평균, 분산, 왜도 m 에 대한 ALD의 n번째 순간은 다음과 같다.
E [ ( x − m ) n ] = n ! λ n ( κ + 1 / κ ) ( κ − ( n + 1 ) − ( − κ ) n + 1 ) {\displaystyle E[(x-m)^{n}={\frac {n! }}{\capta ^{n}(\kappa +1/\kappa )}}\,(\kappa ^{-(n+1)-(-\kappa )^{n+1}}}} 이항 정리 로부터 0에 대한 n번째 순간(m 은 0이 아닌 경우)은 다음과 같다.
E [ x n ] = λ m n + 1 κ + 1 / κ ( ∑ i = 0 n n ! ( n − i ) ! 1 ( m λ κ ) i + 1 − ∑ i = 0 n n ! ( n − i ) ! 1 ( − m λ / κ ) i + 1 ) {\displaystyle E[x^{n}]={\frac {\lambda \,m^{n+1}{\capa +1/\kappa }}}}}\좌측(\sum _{i=0}^{n}}}{\frac {n-i)! }}\,{\frac{1}{(m\\da \kappa )^{i+1}-}-\sum _{i=0}^{n}{\frac {n!}{n-i)! }}\,{\frac{1}{(-m\\da /\kappa )^{i+1}}\오른쪽)} = λ m n + 1 κ + 1 / κ ( e m λ κ E − n ( m λ κ ) − e − m λ / κ E − n ( − m λ / κ ) ) {\displaystyle ={\frac {\lambda \,m^{n+1}}{\kappa +1/\kappa }}\left(e^{m\lambda \kappa }E_{-n}(m\lambda \kappa )-e^{-m\lambda /\kappa }E_{-n}(-m\lambda /\kappa )\right)} 여기서 E n {\displaystyle E_{n}()} 지수 적분 함수 n n Eγ 1 x {\displaysty E_{n}(x)=x^{n-1}\Gamma(1-n,x)
0에 대한 첫 번째 순간은 평균이다.
μ = E [ x ] = m − κ − 1 / κ λ {\displaystyle \mu =E[x]=m-{\frac {\kappa -1/\kappa }{\lambda }}} 분산은 다음과 같다.
σ 2 = E [ x 2 ] − μ 2 = 1 + κ 4 κ 2 λ 2 {\displaystyle \sigma ^{2}=E[x^{2}]-\mu ^{2}={\frac {1+\kappa ^{4}}{\kappa ^{2}\lambda ^{2}}: 왜도는 다음과 같다.
E [ x 3 ] − 3 μ σ 2 − μ 3 σ 3 = 2 ( 1 − κ 6 ) ( κ 4 + 1 ) 3 / 2 {\displaystyle {\frac {E[x^{3}]-3\mu \sigma ^{2}-\mu ^{3}}}={\frac {2\좌측(1-\cappa ^{6}\우측)}{\appa ^{4}+1/2}}: 비대칭 Laplace 변수 생성 비대칭 래플라스 변수(X )는 다음과 같은 방법으로 간격의 균일한 분포에서 도출된 무작위 변수 U 에서 생성될 수 있다.
X = m − 1 λ s κ s 통나무를 하다 ( 1 − U s κ S ) {\displaystyle X=m-{\frac {1}{\lambda \,s\kappa ^{s}}\log(1-U\,s\s\cappa ^{S})} 여기서 s=sgn(U) null
두 지수 분포 의 차이로도 생성될 수 있다. 평균과 비율이 있는 지수 분포에서 X 를1 그리고 평균과 비율이 있는 지수 분포에서 X 를2 구하면(m1-m21 2 , λ, κ) 모수가 있는 비대칭 래플라스 분포에 따라 X1 - X 를2 구한다(m1-m2 , λ, κ).
엔트로피 ALD의 차동 엔트로피는
H = − ∫ − ∞ ∞ f A L ( x ) 통나무를 하다 ( f A L ( x ) ) d x = 1 − 통나무를 하다 ( λ κ + 1 / κ ) {\displaystyle H=-\int _{-\int }^{\f_{AL}(x)\log(f_{AL})(x)dx=1-\log \left({\fraca {\lambda }{\lambda +1/\cappa }}}오른쪽)} ALD는 x s fixed displaystyle (x-m)\,s\ cappa ^{s}} s sgn x ){\displaystysty =\s-m
대체 파라메트리징 대체 파라메트리제이션은 특성 함수에 의해 가능하다.
φ ( t ; μ , σ , β ) = e i μ t 1 − i β σ t + σ 2 t 2 {\displaystyle \varphi(t;\mu ,\mu t}={\frac {e^{i\mu t}{1-i\mu t}}{2}t^{2}}:
여기서 μ[\displaystyle \mu } 위치 매개 변수, μ[\displaystyle \ mu 척도 매개 변수, β[\displaystyle ( 비대칭 매개 변수다. 이것은 Lihn의 섹션 2.6.1과 섹션 3.1(2015)에 명시되어 있다. [3] 확률밀도함수는
f ( x ; μ , σ , β ) = 1 2 σ B 0 { 생략하다 ( x − μ σ B − ) 만일 x < μ 생략하다 ( − x − μ σ B + ) 만일 x ≥ μ {\displaystyle f(x;\mu ,\sigma ,\beta )={\frac {1}{2\sigma B_{0}}}{\begin{cases}\exp \left({\frac {x-\mu }{\sigma B^{-}}}\right)&{\text{if }}x<\mu \\[4pt]\exp(-{\frac {x-\mu }{\sigma B^{+}}}) &{\text{if }x\geq \mu \end{case}} where B 0 = 1 + β 2 / 4 {\displaystyle B_{0}={\sqrt {1+\beta ^{2}/4}}} B ± = B 0 ± β / 2 {\displaystyle B^{\pm }=B_{0}\pm \beta /2} B + B − = 1 , B + − B − = β {\displaystyle B^{+}B^{-}=1,\P B^{+}-B^{-}=\beta }
μs(μs) .
E [ ( x − μ ) n ] = σ n n ! 2 B 0 ( ( B + ) n + 1 + ( − 1 ) n ( B − ) n + 1 ) {\displaystyle E[(x-\mu )^{n}]={\frac {\sigma ^{n}n! }{2B_{0}}((B^{+})^{n+1}+(-1)^{n}(B^{-})^{n+1}}}} 0에 대한 평균은 다음과 같다.
E [ x ] = μ + σ β \displaystyle E[x]=\mu +\sigma \beta \beta }
분산은 다음과 같다.
E [ x 2 ] − E [ x ] 2 = σ 2 ( 2 + β 2 ) {\displaystyle E[x^{2}]-E[x]^{2}=\sigma ^{2}(2+\beta ^{2})}
왜도:
2 β ( 3 + β 2 ) ( 2 + β 2 ) 3 / 2 {\displaystyle {\frac {2\properties (3+\properties ^{2})}{{3/2}}:
과도한 첨도는 다음과 같다.
6 ( 2 + 4 β 2 + β 4 ) ( 2 + β 2 ) 2 {\displaystyle {\frac {6(2+4\filename ^{2}+\filename ^{4}}}}{{2+\filename ^{2}}}}}}:{2}}:
작은 β {\displaystyle \beta } , 약 3 2 displaystyle \beta /{\sqrt{2}}. β displaystyle \beta} null
참조
이산형 일변도의
연속 일변도의
의 지지를 받고 있는. 경계 간격 의 지지를 받고 있는. 반무한 간격을 두고 지지의 대체로 실선 지지하여 누구의 타입이 다른가.
혼합 일변도의
다변량 (공동) 방향 퇴보하다 그리고 단수 가족들











![{\displaystyle f(x;m,\lambda ,\kappa )={\frac {\lambda }{\kappa +1/\kappa }}{\begin{cases}\exp \left((\lambda /\kappa )(x-m)\right)&{\text{if }}x<m\\[4pt]\exp(-\lambda \kappa (x-m))&{\text{if }}x\geq m\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c7a5880e8c96c7d3d9ed3535662995f5617bb7aa)
![{\displaystyle F(x;m,\lambda ,\kappa )={\begin{cases}{\frac {\kappa ^{2}}{1+\kappa ^{2}}}\exp((\lambda /\kappa )(x-m))&{\text{if }}x\leq m\\[4pt]1-{\frac {1}{1+\kappa ^{2}}}\exp(-\lambda \kappa (x-m))&{\text{if }}x>m\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/85d189b9f7550d0f6aacf6cb9a37c6fca822f313)







![{\displaystyle E[(x-m)^{n}]={\frac {n!}{\lambda ^{n}(\kappa +1/\kappa )}}\,(\kappa ^{-(n+1)}-(-\kappa )^{n+1})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a8868fefb958277e67a7712b289ea495c74cb97)
![{\displaystyle E[x^{n}]={\frac {\lambda \,m^{n+1}}{\kappa +1/\kappa }}\,\left(\sum _{i=0}^{n}{\frac {n!}{(n-i)!}}\,{\frac {1}{(m\lambda \kappa )^{i+1}}}-\sum _{i=0}^{n}{\frac {n!}{(n-i)!}}\,{\frac {1}{(-m\lambda /\kappa )^{i+1}}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a158df93e9b0dee54ecc0b37e8c9ad5d284dfaa3)

 .
.![{\displaystyle \mu =E[x]=m-{\frac {\kappa -1/\kappa }{\lambda }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3bc47c54a7c64db622d4b4146a9d035f7ccbce4e)
![{\displaystyle \sigma ^{2}=E[x^{2}]-\mu ^{2}={\frac {1+\kappa ^{4}}{\kappa ^{2}\lambda ^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6acfa777e33568bff3badd818d64aae530a856c3)
![{\displaystyle {\frac {E[x^{3}]-3\mu \sigma ^{2}-\mu ^{3}}{\sigma ^{3}}}={\frac {2\left(1-\kappa ^{6}\right)}{\left(\kappa ^{4}+1\right)^{3/2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/307691af7da4ffb9fa266dd40953ca32569d1ac6)





 (는)
(는) 

![{\displaystyle f(x;\mu ,\sigma ,\beta )={\frac {1}{2\sigma B_{0}}}{\begin{cases}\exp \left({\frac {x-\mu }{\sigma B^{-}}}\right)&{\text{if }}x<\mu \\[4pt]\exp(-{\frac {x-\mu }{\sigma B^{+}}})&{\text{if }}x\geq \mu \end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4bfcba0923f2a185af04d05ff4696d9d3b3ecf8c)



![{\displaystyle E[(x-\mu )^{n}]={\frac {\sigma ^{n}n!}{2B_{0}}}((B^{+})^{n+1}+(-1)^{n}(B^{-})^{n+1})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ad40fc5040ee23928ef521827361c8fd86f71b4)
![{\displaystyle E[x]=\mu +\sigma \beta }](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ccca77aabf5199e09f7a8e037ab39ec09703bfd)
![{\displaystyle E[x^{2}]-E[x]^{2}=\sigma ^{2}(2+\beta ^{2})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b4ba9cb3233d7b1ab1a182d0289021a94ca9648)





