스큐 정규 분포
Skew normal distribution| 확률밀도함수 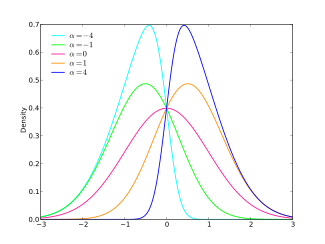 | |||
| 누적분포함수 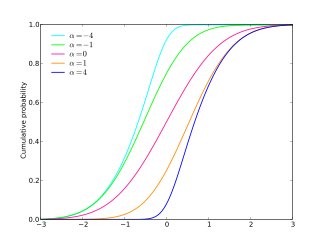 | |||
| 매개변수 | 위치(실제) 척도(양수, 실제) 모양(실제) | ||
|---|---|---|---|
| 지원 | |||
| CDF | ( ,) 는 오웬의 T 함수다. | ||
| 평균 | + 2 Δ 2\{\+\omega {2여기서 = + \ \ | ||
| 모드 | |||
| 분산 | |||
| 왜도 | |||
| 엑스트라 쿠르토시스 | |||
| MGF | |||
| CF | |||
확률 이론과 통계에서 스큐 정규 분포는 정규 분포를 일반화하는 연속 확률 분포로 0이 아닌 왜도를 허용한다.
정의
( ) 이(가) 표준 정규 확률 밀도 함수를 나타내도록 하십시오.
다음과 같은 누적 분포 함수를 사용하여
- ,
여기서 "erf"는 오류 함수다. 그런 다음 매개변수 }을(를) 갖는 스큐 정규 분포의 확률 밀도 함수(pdf)를 다음과 같이 제공한다.
이 분포는 오헤이건과 레너드(1976년)가 처음 도입했다.[1] 이 분포에 대한 대체 형태는 해당 수량 함수와 함께 아슈르와 압델-하미드가[2], 무드홀카르와 허슨이 제공했다.[3]
분포를 뒷받침하는 확률적 과정은 안델, 네투카, 즈바라(1984)가 설명했다.[4] 분포와 그 확률적 공정 기반은 모두 Chan과 Tong(1986)에서 개발된 대칭 논거의 결과였으며,[5] 이는 다변량 t 분포 등 정규성을 벗어난 다변량 사례에 적용된다. The distribution is a particular case of a general class of distributions with probability density functions of the form where is any PDF symmetric about zero and is any CDF whose PDF는 0에 대칭이다.[6]
여기에 위치 및 척도 파라미터를 추가하기 위해 통상적인 x→ x - x = 일 때 정규 분포가 회복되는지 확인할 수 있으며, 절대값인 디스플레이 증가. 분포는 > 일 경우 오른쪽으로 치우치고, < {\일 경우 왼쪽으로 치우친다 위치 Ω{\ 매개 변수 이(가) 있는 확률밀도 함수는 다음과 같이 된다.
그러나 분포의 왜도( ( })는 간격- ,) )으로 제한된다는 점에 유의하십시오
표시된 바와 같이 분포의 모드(최대)는 고유하다.[7] 일반 의 경우 에 대한 분석 식이 없지만 상당히 정확한(숫자적) 근사치는 다음과 같다.
여기서 = 2Δ{\{z}{\}}\ _
추정
}에 대한 최대우도 추정치는 숫자로 계산할 수 있지만, = 이 아니면 추정치에 대해 폐쇄형 식을 사용할 수 없다 폐쇄형식이 필요할 경우, 모멘트 방법을 적용할 수 있다.ed는 왜도 방정식을 뒤집어서 샘플 스큐로부터 을(를) 추정한다. 이것은 예상치를 산출한다.
여기서 = + 2 ^ 샘플 스큐이다. 의 부호는 1의 부호와 같다 따라서 = /1 -
The maximum (theoretical) skewness is obtained by setting in the skewness equation, giving . However it is possible that the sample skewness is larger, and then cannot be determined from these equations. When using the method of moments in an automatic fashion, for example to give starting values for maximum likelihood iteration, one should therefore let (for example)
스큐 정상방법이 이를 바탕으로 한 추론의 신뢰성에 미치는 영향에 대한 우려가 표출되고 있다.[8]
관련 분포
기하급수적으로 수정된 정규 분포는 정규 분포를 치우친 사례로 일반화하는 또 다른 3-모수 분포다. 스큐 노멀은 여전히 스큐 방향에서 정상과 같은 꼬리를 가지며, 다른 방향에서는 짧은 꼬리가 있다. 즉, 스큐의 밀도는 포지티브 e - k 에 점증적으로 비례한다 따라서 무작위성의 7가지 상태를 보면 "적절한 경미한 무작위성"을 나타낸다. 이와는 대조적으로, 기하급수적으로 변형된 정상의 꼬리는 꼬치 방향으로 지수적인 꼬리를 가지고 있다; 그 밀도는 으로 e- x x에 비례한다 같은 용어로, "경계 경미한 무작위성"을 나타낸다.
따라서 스큐 정규 분포는 정규 분포보다 더 많은 특이치가 없는 편향된 분포를 모형화하는 데 유용한 반면, 기하급수적으로 수정된 정규 분포는 한 방향에서 특이치의 발생률이 증가하는 경우에 유용하다.
참고 항목
참조
- ^ O'HAGAN, A.; LEONARD, TOM (1976). "Bayes estimation subject to uncertainty about parameter constraints". Biometrika. 63 (1): 201–203. doi:10.1093/biomet/63.1.201. ISSN 0006-3444.
- ^ Ashour, Samir K.; Abdel-hameed, Mahmood A. (October 2010). "Approximate skew normal distribution". Journal of Advanced Research. 1 (4): 341–350. doi:10.1016/j.jare.2010.06.004. ISSN 2090-1232.
- ^ Mudholkar, Govind S.; Hutson, Alan D. (February 2000). "The epsilon–skew–normal distribution for analyzing near-normal data". Journal of Statistical Planning and Inference. 83 (2): 291–309. doi:10.1016/s0378-3758(99)00096-8. ISSN 0378-3758.
- ^ 안델, J, 네투카, I. 및 Zvara, K.(1984) 임계값 자기 회귀 프로세스. 키베르네티카, 20, 89-106
- ^ Chan, K. S.; Tong, H. (March 1986). "A note on certain integral equations associated with non-linear time series analysis". Probability Theory and Related Fields. 73 (1): 153–158. doi:10.1007/bf01845999. ISSN 0178-8051. S2CID 121106515.
- ^ Azzalini, A. (1985). "A class of distributions which includes the normal ones". Scandinavian Journal of Statistics. 12: 171–178.
- ^ Azzalini, Adelchi; Capitanio, Antonella (2014). The skew-normal and related families. pp. 32–33. ISBN 978-1-107-02927-9.
- ^ 퓨지, 아서 "아잘리니의 왜소 분포에 대한 추론 문제" 적용통계저널 27.7(2000년) : 859-870
















![\Phi (x)=\int _{{-\infty }}^{{x}}\phi (t)\ dt={\frac {1}{2}}\left[1+\operatorname {erf}\left({\frac {x}{{\sqrt {2}}}}\right)\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/b64168aa76f440a9ab0071082ed917dee8b8a4b6)

























 점증적으로 비례한다
점증적으로 비례한다



