나카가미 분포
Nakagami distribution| 확률밀도함수 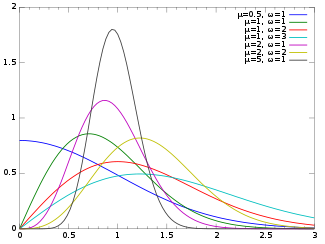 | |||
| 누적분포함수 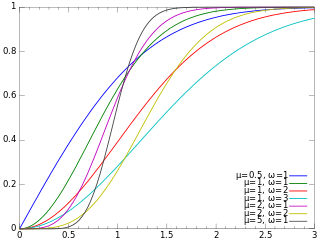 | |||
| 매개변수 | 0.5 0. 모양(실제) > 스프레드(실제) | ||
|---|---|---|---|
| 지원 | |||
| CDF | |||
| 평균 | |||
| 중앙값 | 단순 닫힘 양식 없음 | ||
| 모드 | |||
| 분산 | |||
나카가미 분포 또는 나카가미-m 분포는 감마 분포와 관련된 확률 분포다. 나카가미 분포 패밀리는 형상 모수 ≥ / 1과 확산 > 의 두 번째 모수를 가진다
특성화
여기서( / > 0) 1/및
여기서 P는 정규화(하위) 불완전한 감마함수다.
파라메트리제이션
매개 변수 및 은[2](는)
그리고
모수 추정
다른 방법으로 분포를 적합시키는 방법은 σ = Ω/m 및 m으로 파라메트리 {\} 및 m을 = = Ω/m 및 m로 재모수하는 것이다.[3]
나카가미 로부터 1 x , …, n= x n {\{1x_{n을(를) 받으면 우도 함수는 다음과 같다.
그 로그는
그러므로
이 파생상품들은 오직 다음에야 사라진다.
m에 관한 파생상품이 소멸되는 m 값은 뉴턴-래프슨 방법을 포함한 수치적 방법에 의해 발견된다.
임계 지점에서 전지구적 최대치가 달성되므로 임계점은 (m,³)의 최대 우도 추정치임을 알 수 있다. 최대 우도 추정의 공차 때문에 Ω에 대한 MLE도 얻는다.
세대
나카가미 분포는 감마 분포와 관련이 있다. In particular, given a random variable , it is possible to obtain a random variable , by setting , 및 의 제곱근 사용
나카가미 분포 ; m ,) 을(를) 로 설정한 후 무작위 변수의 스케일 변환에 따라 카이 분포에서 생성할 수 있다. 즉, 나카가미 랜덤 X 은(는) 아래와 같이 카이 분산 랜덤 변수 Y~ ()2m에 단순한 스케일 변환에 의해 생성된다.
카이-분포의 경우 자유도 (\ 2m는 정수여야 하지만 나카가미의 경우 은 1/2보다 큰 실제 숫자가 될 수 있다. 이것이 결정적인 차이이므로 나카가미-m은 치-제곱 분포의 일반화로 간주되는 감마 분포와 유사하게 치-제곱 분포의 일반화로 간주된다.
기록 및 응용 프로그램
나카가미 분포는 1960년에 처음 제안되어 비교적 새로운 것이다.[4] 그것은 여러 경로를[5] 가로지르는 무선 신호의 감쇠를 모델링하고 사라지는 채널이 무선 통신에 미치는 영향을 연구하기 위해 사용되어 왔다.[6]
관련 분포
"극좌표(반경과 각도)로 다시 쓰여진 이바리산 정상 랜덤 변수의 참 평균 주위의 반경은 호이트 분포를 따른다. 이와 동등하게, 복합 정규 랜덤 변수의 계수는 다음과 같다.
- 2m = k로 나카가미 분포는 스케일링된 기 분포를 제공한다.
- = 나카가미 분포는 스케일링 반 정규 분포를 제공한다
- 나카가미 분포는 일반화된 감마 분포의 특정한 형태로서 p = 2 및 d = 2m이다.
참고 항목
참조
- ^ a b Laurenson, Dave (1994). "Nakagami Distribution". Indoor Radio Channel Propagation Modelling by Ray Tracing Techniques. Retrieved 2007-08-04.
- ^ R. Kolar, R. Jirik, J. Jan(2004) "나카가미-m 매개변수의 추정기 비교 및 초음파 검사에서의 적용" 13(1), 8–12, 라디오 엔지니어링
- ^ Mitra, Rangeet; Mishra, Amit Kumar; Choubisa, Tarun (2012). "Maximum Likelihood Estimate of Parameters of Nakagami-m Distribution". International Conference on Communications, Devices and Intelligent Systems (CODIS), 2012: 9–12.
- ^ 나카가미, M. (1960) "급속 페이딩의 강도의 일반적인 공식인 m-Distribution" William C에서. Hoffman, 편집자, 전파 전파의 통계적 방법: 1958년 6월 18~20일 열린 심포지엄의 진행, 페이지 3~36. 페르가몬 프레스, doi:10.1016/B978-0-08-009306-2.50005-4
- ^ 파슨스, J. D. (1992) 이동 무선 전파 채널. 뉴욕: 와일리.
- ^ Ramon Sanchez-Iborra; Maria-Dolores Cano; Joan Garcia-Haro (2013). Performance evaluation of QoE in VoIP traffic under fading channels. World Congress on Computer and Information Technology (WCCIT). pp. 1–6. doi:10.1109/WCCIT.2013.6618721. ISBN 978-1-4799-0462-4.
- ^ Paris, J.F. (2009). "Nakagami-q (Hoyt) distribution function with applications". Electronics Letters. 45 (4): 210. doi:10.1049/el:20093427.
- ^ "HoytDistribution".
- ^ "NakagamiDistribution".








 확산
확산 




![{\displaystyle m={\frac {\left(\operatorname {E} \left[X^{2}\right]\right)^{2}}{\operatorname {Var} \left[X^{2}\right]}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/170a63e920349b6d319032d3714dd0f6eda4655d)
![{\displaystyle \Omega = \operatorname{E} \left[X^2 \right]. }](https://wikimedia.org/api/rest_v1/media/math/render/svg/24eb21fa6e972b1338b50769c409be9d9f4f7129)














 (는) 아래와 같이
(는) 아래와 같이




