정규 확률도

정규 확률도는 정규성으로부터의 실질적인 이탈을 식별하기 위한 그래픽 기법이다. 여기에는 특이치, 왜도, 첨도, 변환의 필요성 및 혼합물의 식별이 포함된다. 정규 확률도는 원시 데이터, 모형 적합치의 잔차 및 추정된 모수로 만든다.

정규 확률도

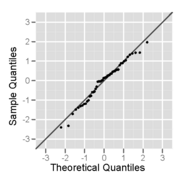
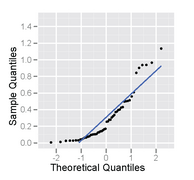
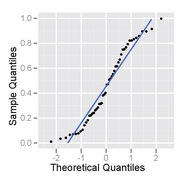
정규 확률도("정규 분포도"라고도 함)에서 정렬된 데이터는 데이터가 거의 정규 분포를 따르는 경우 결과 영상이 직선에 가깝게 보이도록 하기 위해 선택된 값과 비교하여 표시된다. 직선으로부터의 편차는 정규성으로부터의 이탈을 의미한다. 플롯은 정규 확률지라고 불리는 특수 그래프 용지를 사용하여 수동으로 수행할 수 있다. 현대 컴퓨터에서는 보통 소프트웨어로 플롯을 만든다.

정규 확률도는 정규 분포에 대한 Q–Q 확률도의 특별한 경우다. 이론적 분량은 일반적으로 해당 순서 통계량의 평균 또는 중위수의 근사치를 위해 선택된다.

정의

정규 확률도는 정렬된 데이터 대 해당 순서 통계량의 평균 또는 중위수에 대한 근사치를 표시하여 형성된다. 순위표를 참조하십시오. 어떤 것은 수직축에 데이터를 표시하고,^[1] 어떤 것은 수평축에 데이터를 표시한다.^[2]^[3]

다른 출처에서는 순위표에 약간 다른 근사를 사용한다. R(프로그래밍 언어)의 기본 "stats" 패키지에서 "qnorm" 함수에 의해 사용되는 공식은 다음과 같다.

z_{i}=\Phi ^{-1}\왼쪽({\frac {i-a}{n+1-2a}\오른쪽),

$i$ = 1 $, 2$ , $...,$ $n$ 에 대해, 어디에

a

=

n

8

10

인 경우 3/

8

n > 10의 경우 0.5,

$그리고 -1$ is은 표준 정상 퀀텀 함수다.

데이터가 정규 분포의 표본과 일치할 경우 점은 직선에 가깝게 위치해야 한다. 참고로 직선은 점들에 맞출 수 있다. 이 선에서 포인트가 더 다양할수록 정규성에서 이탈한 징후가 더 크다. 표본에 평균 0, 표준 편차 1이 있으면 기울기 1이 있는 선에서 0까지를 사용할 수 있다.

점이 많을수록 선으로부터의 랜덤 편차는 덜 뚜렷해진다. 정규 그림은 보통 점 수가 7개 이하인 경우가 많다. 예를 들어, 2-수준 부분 요인 실험의 포화 모형에서 효과를 표시하는 경우. 점 수가 적으면 랜덤 변동성과 실제적인 편차를 정규성과 구별하기가 어려워진다.

기타분포

정규 분포 이외의 분포에 대한 확률도는 정확히 동일한 방법으로 계산된다. 정규 분량 함수 $φ$ 은⁻¹ 단순히 원하는 분포의 분량 함수로 대체된다. 이러한 방법으로 확률도는 한 분포가 분량 함수를 갖는 분포에 대해 쉽게 생성될 수 있다.

위치 척도 분포의 경우 분포의 위치 및 척도 모수는 절편과 선의 기울기에서 추정할 수 있다. 다른 분포의 경우 확률도를 만들기 전에 먼저 모수를 추정해야 한다.

플롯 유형

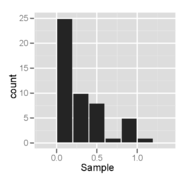
이것은 히스토그램과 정규 확률도로 표시된 정규 분포의 크기 50의 표본이다.

정규 분포에서 추출한 표본의 정규 확률도 - 최소한 몇 개의 크고 작은 값을 무시할 때는 상당히 곧게 보인다.
정규 분포의 표본 히스토그램 - 상당히 대칭적이고 단일하게 보이는 표본

이것은 히스토그램과 정규 확률도로 표시된 오른쪽 기울기 분포에서 50 크기의 표본이다.

오른쪽으로 치우친 분포에서 추출한 표본의 정규 확률도 - C 모양이 반전되어 있다.
오른쪽으로 치우친 분포에서 표본의 히스토그램 - 단일하고 오른쪽으로 치우쳐 보인다.

이것은 히스토그램과 정규 확률도로 표시된 균일한 분포에서 크기 50의 표본이다.

균일한 분포에서 추출한 표본의 정규 확률도 - S 모양이 있다.
균일한 분포에서 추출한 표본의 히스토그램 - 다모드로 보이며 대략 대칭으로 보인다.

참고 항목

참조

이 글은 국립표준기술원 웹사이트 https://www.nist.gov의 공공 도메인 자료를 통합한 것이다.

^ 예: 챔버스 외 연구진(1983, ch. 6. 데이터에 대한 분포 가정 평가, 페이지 194)
^ Box, George E. P.; Draper, Norman (2007), Response Surfaces, Mixtures, and Ridge Analysis (2nd ed.), Wiley, ISBN 978-0-470-05357-7
^ Titterington, D. M.; Smith, A. F. M.; Makov, U. E. (1985), "4. Learning about the parameters of a mixture", Statistical Analysis of Finite Mixture Distributions, Wiley, ISBN 0-471-90763-4

추가 읽기

Chambers, John; William Cleveland; Beat Kleiner; Paul Tukey (1983). Graphical Methods for Data Analysis. Wadsworth.

외부 링크

[1] 예: 챔버스 외 연구진(1983, ch. 6. 데이터에 대한 분포 가정 평가, 페이지 194)

[2] Box, George E. P.; Draper, Norman (2007), Response Surfaces, Mixtures, and Ridge Analysis (2nd ed.), Wiley, ISBN 978-0-470-05357-7

[3] Titterington, D. M.; Smith, A. F. M.; Makov, U. E. (1985), "4. Learning about the parameters of a mixture", Statistical Analysis of Finite Mixture Distributions, Wiley, ISBN 0-471-90763-4

[1]

[2]

[3]

v t 분배 피팅
개요 및 방법	확률도 정규 확률도 P-P 그림 Q–Q 그림 플로팅 위치 L-moment 분배 피팅 누적빈도분석
소프트웨어	컴프렉 매트릭웍스 R StatSoft

Search

정규 확률도

네임스페이스

더

목차

정의

기타분포

플롯 유형

참고 항목

참조

추가 읽기

외부 링크