신뢰 구간
Confidence interval빈도 통계량에서 신뢰 구간(CI)은 알 수 없는 모수에 대한 추정치의 범위입니다.신뢰 구간은 지정된 신뢰 수준에서 계산됩니다. 95% 신뢰 수준이 가장 일반적이지만 90% 또는 99%와 같은 다른 수준이 [1][2]사용되는 경우도 있습니다.신뢰 수준은 모수의 참 값을 포함하는 해당 CI의 장기 실행 비율을 나타냅니다.예를 들어 95% 수준에서 계산된 모든 구간 중 95%는 모수의 참 [3]값을 포함해야 합니다.
CI 폭에 영향을 미치는 요인에는 신뢰 수준, 표본 크기 및 [4]표본의 변동성이 포함됩니다.다른 모든 사항은 동일하지만 표본이 클수록 신뢰 구간이 좁아집니다.마찬가지로 표본의 변동성이 클수록 신뢰 구간이 넓어지고 신뢰 수준이 높을수록 신뢰 [5]구간이 넓어집니다.
정의.
X를 확률분포에서 랜덤 표본으로 추정할 수 있는 수량인 통계적 모수 θ와 당장 관심 없는 수량인 θ를 나타낸다.파라미터 θ에 대한 신뢰구간(신뢰수준 또는 계수 θ)은 다음과 같은 특성을 가진 랜덤 변수 u(X) 및 v(X)에 의해 결정되는 구간(u(X), v(X)이다.
전형적인 값이 1에 가깝지만 크지 않은 숫자 θ는 1 - α(또는 백분율 100%·(1 - α)) 형식으로 지정되기도 한다. 여기서 α는 음이 아닌 작은 수치이며, 가장 일반적으로 0.05이다.
u(X)와 v(X)는 X가 랜덤으로 수집되는 한 신뢰구간을 계산할 때마다 추정되는 파라미터의 참값인 θ를 포함할 가능성이 있음을 명시하는 것이 중요하다.이것은, 실제의 「」와 「」[2]에 대해서 유효하게 됩니다.
대략적인 신뢰 구간
많은 응용 프로그램에서 정확히 필요한 신뢰 수준을 갖는 신뢰 구간을 구성하기는 어렵지만 대략적인 구간을 계산할 수 있습니다.인터벌을 구성하는 규칙은 다음과 같은 경우 {\(\에서 신뢰구간을 제공하는 것으로 받아들여질 수 있습니다.
허용 가능한 근사치 수준까지.또는 일부 저자는[6] 단순히 다음을 요구한다.
이는 확률이 부분적으로만 확인되거나 부정확한 경우, 그리고 이산 분포를 다룰 때도 유용합니다.폼의 신뢰 한계
- ( (X )<{\ {\displaydisplay {\ {\ \ style \ } ( ( X ) <\)\ } Pr( < ()) {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ \ style \ \ < ( X teq \ )
보수적이라 불리며,[7] 따라서 보수적 신뢰구간과 일반적으로 지역을 말한다.
바람직한 속성
표준통계절차를 적용할 때, 신뢰구간을 구성하는 표준방법이 있는 경우가 많다.이것들은 특정 바람직한 속성을 충족하기 위해 고안될 것이며, 이는 절차가 의존하는 가정이 참임을 고려할 때 유지될 것이다.이러한 바람직한 속성은 유효성, 최적성 및 불변성으로 설명할 수 있습니다.이러한 "유효성"이 가장 중요하며, "최적성"이 그 뒤를 잇는다."불변성"은 구간을 구성하기 위한 규칙보다는 신뢰구간 도출 방법의 속성으로 간주될 수 있다.비표준 어플리케이션에서도 동일한 바람직한 속성이 요구됩니다.
- 타당성.즉, 신뢰 구간의 공칭 범위 확률(신뢰 수준)이 정확히 또는 양호한 근사치로 유지되어야 합니다.
- 최적성.즉, 신뢰 구간을 구성하는 규칙은 데이터 세트의 정보를 최대한 활용해야 합니다.데이터셋의 절반은 버려도 유효한 신뢰구간을 도출할 수 있다는 점을 상기해 주십시오.최적성을 평가하는 한 가지 방법은 신뢰 구간을 구성하는 규칙이 일반적으로 길이가 짧은 구간으로 이어지는 경우 신뢰 구간을 구성하는 규칙이 다른 규칙보다 더 잘 판단되도록 하는 것입니다.
- 불변성.많은 어플리케이션에서 추정되는 수량은 엄밀하게 정의되지 않을 수 있습니다.예를 들어, 설문조사는 모집단의 중위소득 추정치를 산출할 수 있지만, 이것이 그래픽 결과를 나타내기 위한 공통 척도이기 때문에 중위소득의 로그 추정치를 제공하는 것으로 동일하게 간주할 수 있다.중위소득에 대한 신뢰구간 구성에 사용된 방법은 중위소득의 대수에 대한 신뢰구간 구성에 적용할 때 동등한 결과를 제공하는 것이 바람직할 것이다. 특히, 후자구간 끝의 값은 이전 인터의 끝의 값 로그가 될 것이다.값
파생 방법
비표준 어플리케이션의 경우 신뢰구간 구축 규칙을 도출하기 위해 몇 가지 루트를 사용할 수 있습니다.표준 절차에 대해 확립된 규칙은 이러한 경로 중 몇 가지를 통해 정당화되거나 설명될 수 있습니다.일반적으로 신뢰 구간을 구성하는 규칙은 고려 중인 수량의 점 추정치를 찾는 특정 방법과 밀접하게 연관되어 있습니다.
- 요약 통계
- 이것은 추정을 위한 모멘트의 방법과 밀접하게 관련되어 있다.간단한 예제는 추정할 수량이 모집단 평균인 경우 발생하며, 이 경우 자연 추정치가 표본 평균입니다.마찬가지로 표본 분산을 사용하여 모집단 분산을 추정할 수 있습니다.참 평균에 대한 신뢰 구간은 표본 분산의 제곱근의 배수인 폭을 사용하여 표본 평균을 중심으로 구성할 수 있습니다.
- 우도론
- 추정치는 최대우도 원칙을 사용하여 구성할 수 있으며, 이에 대한 우도 이론은 추정치에 대한 신뢰 구간 또는 신뢰 영역을 구성하는 두 가지 방법을 제공합니다.
- 추정식
- 여기서의 추정 접근방식은 모멘트 방법의 일반화 및 최대우도 접근방식의 일반화 둘 다로 간주될 수 있다.추정 방정식에서 [citation needed]도출된 추정치에 기초하여 신뢰 구간을 구성할 수 있는 최대우도 이론의 결과에는 상응하는 일반화가 있습니다.
- 가설 검정
- 모수의 일반 값에 대해 가설 검정을 사용할 수 있는 경우 실제 값이 주어진 값이라는 귀무 가설에 대한 가설 검정이 유의 수준(1 - p)[8]에서 기각되지 않는 모든 점을 100% 신뢰 영역에 포함시켜 신뢰 구간/영역을 구성할 수 있습니다.
- 부트스트랩
- 상기 방법에 대한 분포 가정이 불확실하거나 위반되는 상황에서는 재샘플링 방법을 사용하여 신뢰 구간 또는 예측 구간을 구성할 수 있다.관측된 데이터 분포와 내부 상관관계는 더 넓은 모집단에서 상관관계를 대신하는 것으로 사용됩니다.다음 항목도 참조하십시오.부트스트랩 배포에서 신뢰구간 도출
- 중심 한계 정리는 큰 수의 법칙을 정교하게 하는 것이다.분산이 유한한 다수의 독립적 랜덤 1, n{ ..., }}의 경우 평균 n{\ { 은 분포에 관계없이 약 정규 분포를 가진다. 이에요.[2]
예
{X1, …, Xn}이(가) 알 수 없는 모수 평균 μ 및 분산 θ을2 가진 정규 분포 모집단으로부터 독립적인 표본이라고 가정합니다.허락하다
여기서 X는 표본 평균이고2 S는 표본 분산입니다.그리고나서
자유도가 [9]n - 1인 Student's t 분포가 있습니다.T의 분포는 관측 불가능한 매개변수 μ 및 θ의2 값에 의존하지 않으며, 즉 중추량이다.μ에 대한 95% 신뢰 구간을 계산하려고 합니다.그런 다음 c를 이 분포의 97.5백분위수로 나타내면
앞의 식에서는 "97.5th"와 "0.95"가 올바릅니다.T T가 스타일 -c보다작을 확률은 2.5%, ++c보다클 확률은 2.5%입니다. T T가 -c 와+c(style + 사이일 은 95%입니다.
그 결과,
그리고 우리는 μ에 대한 이론적인 95% 신뢰 구간을 가지고 있다.
표본을 관찰한 후 X에 대한 값 x와 S에 대한 값 s를 찾아 신뢰 구간을 계산합니다.
해석
신뢰 구간에 대한 다양한 해석을 제공할 수 있습니다(다음의 예시로 95% 신뢰 구간을 사용).
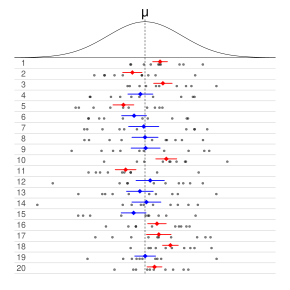
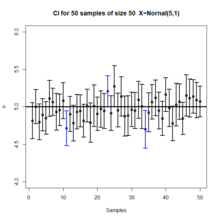
- 신뢰 구간은 반복 샘플(또는 재샘플링)의 장기 실행 주파수로 표시할 수 있습니다."이 절차를 여러 표본에 대해 반복한다면 모집단 모수의 실제 값을 포함하는 계산된 95% 신뢰 구간의 비율은 95%[10]에 가까워질 것입니다."
- 신뢰 구간은 단일 이론(아직 실현되지 않은) 표본에 대한 확률로 표현될 수 있다. "앞으로 주어진 표본에서 계산한 95% 신뢰 구간이 모집단 모수의 실제 값을 포함할 확률이 95%이다."[11] 이는 기본적으로 "반복 샘플" 해석을 빈도가 아닌 확률로 재구성합니다.Neyman 건축을 참조하십시오.
- 신뢰구간은 통계적 유의성의 관점에서 표현될 수 있다."95% 신뢰 구간은 통계적으로 0.05 수준의 점 추정치와 유의하게 다르지 않은 값을 나타냅니다."[12]
일반적인 오해
신뢰 구간과 수준은 종종 오해를 받고 있으며, 발표된 연구에 따르면 전문 과학자들도 종종 이를 [13][14][15][16][17][18]잘못 해석하는 것으로 나타났다.
- 95% 신뢰 수준은 주어진 실현 구간에서 모집단 모수가 구간 내에 있을 확률이 95%라는 것을 의미하지 않습니다(즉, 구간이 모집단 [19]모수를 포함할 확률이 95%).엄격한 빈도론자의 해석에 따르면 일단 간격이 계산되면 이 간격은 파라미터 값을 포함하거나 포함하지 않으므로 더 이상 확률의 문제가 되지 않습니다.95% 확률은 특정 계산된 [20]구간이 아니라 추정 절차의 신뢰성과 관련이 있습니다.네이먼 본인은(신뢰구간의 원래 지지자) 자신의 원본 [11]논문에서 다음과 같이 지적했다.
"상기 설명에서 확률 진술은 통계학자가 앞으로 우려할 추정의 문제를 가리킨다는 것을 알 수 있습니다.사실, 나는 정확한 결과의 빈도는 α가 될 것이라고 여러 번 말했다.이제 표본이 이미 그려지고 계산에 [특정 한계]가 주어진 경우를 생각해 봅시다.이 특별한 경우에 [이 한계 사이에] 참값의 확률은 α라고 말할 수 있는가?대답은 분명히 부정적이다.매개 변수는 알 수 없는 상수이며 값에 대한 확률 문을 만들 수 없습니다.."
- Deborah Mayo는 이에 대해 다음과 [21]같이 더 자세히 설명합니다.
그러나 Neyman-Pearson 이론은 [데이터의] 값을 본 후 형성된 특정 신뢰 구간이 (1 - α)100% 확률 또는 (1 - α)100%의 신뢰도로 0의 참 값을 포함한다고 결론짓는 것을 허용하지 않는다는 점을 강조해야 한다.세이든펠드의 발언은 네이만-피어슨이 합법적으로 제공할 수 없는 무언가를 제공하고자 하는 (흔하지 않은) 신뢰 구간에 뿌리를 둔 것으로 보인다. 즉, 알려지지 않은 매개변수 값이 특정 구간에 있다는 확률, 믿음 또는 뒷받침의 정도에 대한 척도이다.Savage(1962)에 이어 특정 간격에 매개변수가 있을 확률은 최종 정밀도 측정이라고 할 수 있다.최종 정밀도 측정이 바람직해 보일 수 있고 신뢰수준이 그러한 측정치를 제공하는 것으로 해석되는 경우가 종종 있지만, 그러한 해석은 보증되지 않는다.물론 이런 잘못된 해석은 자신감이라는 단어에서 비롯된다.
- 95% 신뢰 수준은 표본 데이터의 95%가 신뢰 구간 내에 있다는 것을 의미하지 않습니다.
- 신뢰 구간은 종종 경험적으로 타당한 값의 범위로 간주되지만 표본 모수에 대한 타당한 값의 최종 범위는 아닙니다.
- 실험에서 계산된 특정 신뢰 수준이 95%라고 해서 실험 반복실험의 표본 모수가 [17]이 구간 내에 속할 확률이 95%인 것은 아닙니다.
반례례
신뢰 구간 이론이 제안된 이후, 적어도 누군가가 신뢰 구간을 순진하게 해석하는 경우 신뢰 구간의 해석이 어떻게 문제가 될 수 있는지를 보여주기 위해 이론에 대한 많은 반증 사례들이 개발되었다.
균일한 위치에 대한 신뢰 절차
Welch는[22] 신뢰구간 이론과 (피셔의 기준구간과 객관적인 베이지안구간 포함) 구간추정의 다른 이론 사이의 차이를 명확히 보여주는 예를 제시했다.로빈슨은[23] 이 예를 "믿을 수 있을 만큼 네이먼의 신뢰 구간 이론의 가장 잘 알려진 반례"라고 불렀다.웰치에게는 신뢰구간 이론의 우위성을, 이론의 비판자에게는 결함을 보여준다.여기에서는 간략화된 버전을 제시합니다.
1, 2({가 균일한 분포(' - 1/2, ' + 1/2)로부터 독립된 관측치라고 합니다.그러면 최적의 50% 신뢰[24] 절차는 다음과 같습니다.
기준 또는 객관적인 베이지안 인수를 사용하여 구간 추정치를 도출할 수 있습니다.
50% 신뢰 절차이기도 합니다.Welch는 신뢰 구간 이론의 desiderata에 따라 첫 번째 신뢰 절차가 두 번째 신뢰 절차를 지배한다는 것을 보여주었다. 모든 1 { _ {1 에 대해 첫 번째 절차가 1 { displaystyle 1}을 포함할 확률은 두 번째 신뢰 구간 이론의 확률보다 작거나 같다.절차에는 1 _이 포함됩니다.첫 번째 절차에서 구간의 평균 너비가 두 번째 절차보다 작습니다.따라서, 첫 번째 절차는 고전적인 신뢰 구간 이론에서 선호된다.
단, - 1 / { } - 1/2인 첫 번째 절차부터의 은 true 값 { : 따라서 공칭 50% 신뢰계수는 true va를 포함하는 불확실성과 무관합니다.lue. 두 번째 프로시저에는 이 속성이 없습니다.
또한 첫 번째 절차에서 매우 짧은 간격이 생성되면 X, 2({가 가깝기 때문에 단일 데이터 포인트로만 정보를 제공합니다.그러나 첫 번째 간격은 폭이 짧기 때문에 파라미터의 거의 모든 합리적인 값을 제외합니다.두 번째 절차에는 이 속성이 없습니다.
번째 절차의 두 가지 반직관적 특성은 X1, X }, 가 멀리 떨어져 있을 때 % 와X1, X 2}})가 서로 때 거의 0% 커버리지로 평균 50% 커버리지가 됩니다.그러나 첫 번째 절차가 최적임에도 불구하고, 그 간격은 추정의 정밀도에 대한 평가도 제공하지 않고, 해당 간격이 참 값을 포함한다는 불확실성에 대한 평가도 제공하지 않는다.
이 반례는 신뢰구간의 순진한 해석에 반대하기 위해 사용된다.신뢰 절차가 명목 적용 범위(정밀도에 대한 관계 또는 베이지안 추론과의 관계 등)를 초과하는 속성을 갖는다고 주장되는 경우, 그러한 특성은 증명되어야 한다. 절차가 신뢰 절차라는 사실에서 따르지 않는다.
§에2 대한 신뢰 절차
Steiger는[25] 분산 분석에서 공통 효과 크기 측도에 대한 여러 신뢰 절차를 제안했습니다.모레(알.[19]지적은 이러한 자신감 절차 중 한 명인 그 ω2를 포함하여 몇으로 다가온 F통계 점점 더 ω2—the 신뢰도 간격이 줄어들고 가능한 모든 가치 심지어 0=만 값 ω2을 포함할 수 있다;즉, CI무한소로 좁다는 부적응자 small—indicating이 이 wh 발생하는 속성이 있습니다. p -α / (- ( \ ( - \ % ) 。
이 동작은 신뢰 절차와 유의성 검정 사이의 관계와 일치한다.F가 너무 작아져 그룹 평균이 우연히 예상하는 것보다 훨씬 가까워짐에 따라 유의성 검정에서 θ의 대부분 또는2 모든 값에 대해 거부반응을 나타낼 수 있다.따라서 간격은 매우 좁거나 비어 있습니다(또는 Steiger가 제안한 규칙에 따르면 0만 포함).그러나 이것은 is의2 견적이 매우 정확하다는 것을 의미하지는 않는다.어떤 의미에서는 그 반대인 결과 자체의 신뢰성이 의심스러울 수 있다는 것을 보여준다.이는 신뢰 구간이 추정의 정확성을 나타내는 일반적인 해석과 반대됩니다.
역사
신뢰 구간은 [26]1937년 Jerzy Neyman에 의해 도입되었다.통계학자들은 재빨리 그 아이디어를 받아들였지만, 과학자들에 의한 채택은 더 점진적이었다.의학 저널의 일부 저자들은 1970년대 초에 신뢰 구간을 홍보했다.그럼에도 불구하고 신뢰 구간은 이후 10년 동안 거의 사용되지 않았으며,[27] 그 후 표준이 되었다.1980년대 후반, 의학 저널은 신뢰구간 [28]보고를 요구하기 시작했다.
「 」를 참조해 주세요.
- CLs 상한(입자 물리학)
- 68-95-99.7 규칙
- 신뢰 대역, 곡선에 대한 구간 추정치
- 구간 추정을 위한 베이지안 대안인 신뢰할 수 있는 구간
- 신뢰 분포
- 신뢰 영역, 고차원 일반화
- 크레덴스(통계)
- 누적 분포 함수 기반 비모수 신뢰 구간
- 에러바 – 데이터 가변성을 그래픽으로 표시
- 추정통계
- p-value – 관찰된 샘플 결과의 함수
- 예측 구간, 랜덤 변수에 대한 구간 추정치
- 생각할 수 있는 오류
- 견고한 신뢰 구간
특정 분포에 대한 신뢰 구간
- 이항 분포에 대한 신뢰 구간
- 멱함수 분포의 지수에 대한 신뢰 구간
- 지수 분포의 평균에 대한 신뢰 구간
- 포아송 분포의 평균에 대한 신뢰 구간
- 정규 분포의 평균 및 분산에 대한 신뢰 구간
레퍼런스
- ^ Zar, Jerrold H. (199). Biostatistical Analysis (4th ed.). Upper Saddle River, N.J.: Prentice Hall. pp. 43–45. ISBN 978-0130815422. OCLC 39498633.
- ^ a b c Dekking, Frederik Michel; Kraaikamp, Cornelis; Lopuhaä, Hendrik Paul; Meester, Ludolf Erwin (2005). "A Modern Introduction to Probability and Statistics". Springer Texts in Statistics. doi:10.1007/1-84628-168-7. ISBN 978-1-85233-896-1. ISSN 1431-875X.
- ^ Illowsky, Barbara. Introductory statistics. Dean, Susan L., 1945-, Illowsky, Barbara., OpenStax College. Houston, Texas. ISBN 978-1-947172-05-0. OCLC 899241574.
- ^ Hazra, Avijit (October 2017). "Using the confidence interval confidently". Journal of Thoracic Disease. 9 (10): 4125–4130. doi:10.21037/jtd.2017.09.14. ISSN 2072-1439. PMC 5723800. PMID 29268424.
- ^ Khare, Vikas; Nema, Savita; Baredar, Prashant (2020). Ocean Energy Modeling and Simulation with Big Data Computational Intelligence for System Optimization and Grid Integration. ISBN 978-0-12-818905-4. OCLC 1153294021.
- ^ George G. Rousas(1997) 수학 통계학 강좌, 제2판, 학술 출판사, p397
- ^ Cox D.R., Hinkley D.V.(1974) 이론통계학, 채프먼 & 홀, 페이지 210
- ^ Cox D.R., Hinkley D.V.(1974) 이론통계, 채프먼 & 홀, 섹션 7.2(ii)
- ^ Rees. D.G. (2001) Essential Statistics, 제4판, Chapman 및 Hall/CRC.ISBN 1-58488-007-4 (섹션 9.5)
- ^ Cox D.R., Hinkley D.V.(1974) 이론통계학, Chapman & Hall, p49, p209
- ^ a b Neyman, J. (1937). "Outline of a Theory of Statistical Estimation Based on the Classical Theory of Probability". Philosophical Transactions of the Royal Society A. 236 (767): 333–380. Bibcode:1937RSPTA.236..333N. doi:10.1098/rsta.1937.0005. JSTOR 91337.
- ^ Cox D.R., Hinkley D.V.(1974) 이론통계학, 채프먼 & 홀, 페이지 214, 225, 233
- ^ Kalinowski, Pawel (2010). "Identifying Misconceptions about Confidence Intervals" (PDF). Retrieved 2021-12-22.
- ^ "Archived copy" (PDF). Archived from the original (PDF) on 2016-03-04. Retrieved 2014-09-16.
{{cite web}}: CS1 maint: 제목으로 아카이브된 복사(링크) - ^ Hoekstra, R. D. Morey, J. N. Rouder 및 E-J. Wagenmakers, 2014.신뢰 구간의 강력한 오역.사이코노믹 게시판 리뷰, 언론입니다.[1]
- ^ 과학자들의 신뢰구간 파악은 자신감을 불러일으키지 않는다, 사이언스 뉴스, 2014년 7월 3일
- ^ a b Greenland, Sander; Senn, Stephen J.; Rothman, Kenneth J.; Carlin, John B.; Poole, Charles; Goodman, Steven N.; Altman, Douglas G. (April 2016). "Statistical tests, P values, confidence intervals, and power: a guide to misinterpretations". European Journal of Epidemiology. 31 (4): 337–350. doi:10.1007/s10654-016-0149-3. ISSN 0393-2990. PMC 4877414. PMID 27209009.
- ^ Helske, Jouni; Helske, Satu; Cooper, Matthew; Ynnerman, Anders; Besancon, Lonni (2021-08-01). "Can Visualization Alleviate Dichotomous Thinking? Effects of Visual Representations on the Cliff Effect". IEEE Transactions on Visualization and Computer Graphics. Institute of Electrical and Electronics Engineers (IEEE). 27 (8): 3397–3409. arXiv:2002.07671. doi:10.1109/tvcg.2021.3073466. ISSN 1077-2626. PMID 33856998. S2CID 233230810.
- ^ a b Morey, R. D.; Hoekstra, R.; Rouder, J. N.; Lee, M. D.; Wagenmakers, E.-J. (2016). "The Fallacy of Placing Confidence in Confidence Intervals". Psychonomic Bulletin & Review. 23 (1): 103–123. doi:10.3758/s13423-015-0947-8. PMC 4742505. PMID 26450628.
- ^ "1.3.5.2. Confidence Limits for the Mean". nist.gov. Archived from the original on 2008-02-05. Retrieved 2014-09-16.
- ^ Mayo, D. G. (1981) "Neyman-Pearson 이론의 신뢰구간 방어", 과학철학, 48(2), 269-280. JSTOR 187185
- ^ Welch, B. L. (1939). "On Confidence Limits and Sufficiency, with Particular Reference to Parameters of Location". The Annals of Mathematical Statistics. 10 (1): 58–69. doi:10.1214/aoms/1177732246. JSTOR 2235987.
- ^ Robinson, G. K. (1975). "Some Counterexamples to the Theory of Confidence Intervals". Biometrika. 62 (1): 155–161. doi:10.2307/2334498. JSTOR 2334498.
- ^ Pratt, J. W. (1961). "Book Review: Testing Statistical Hypotheses. by E. L. Lehmann". Journal of the American Statistical Association. 56 (293): 163–167. doi:10.1080/01621459.1961.10482103. JSTOR 2282344.
- ^ Steiger, J. H. (2004). "Beyond the F test: Effect size confidence intervals and tests of close fit in the analysis of variance and contrast analysis". Psychological Methods. 9 (2): 164–182. doi:10.1037/1082-989x.9.2.164. PMID 15137887.
- ^ [Neyman, J., 1937]확률론에 기초한 통계적 추정 이론의 개요.런던 왕립 학회의 철학적인 거래.시리즈 A, 수리 및 물리과학, 236(767), 페이지 333-380]
- ^ Altman, Douglas G. (1991). "Statistics in medical journals: Developments in the 1980s". Statistics in Medicine. 10 (12): 1897–1913. doi:10.1002/sim.4780101206. ISSN 1097-0258.
- ^ Sandercock, Peter A.G. (2015). "Short History of Confidence Intervals". Stroke. Ovid Technologies (Wolters Kluwer Health). 46 (8): e184-7. doi:10.1161/strokeaha.115.007750. ISSN 0039-2499. PMID 26106115.
참고 문헌
- 피셔, R.A.(1956) 통계적 방법과 과학적 추론.올리버와 보이드, 에든버러 (32페이지 참조)
- 프룬트, J.E.(1962) 뉴저지 주 잉글우드 클리프스의 수학 통계 프렌티스 홀(227-228페이지 참조).
- 해킹, I. (1965) 통계적 추론의 논리.캠브리지 대학 출판부, 캠브리지ISBN 0-521-05165-7
- Keeping, E.S. (1962) 통계적 추론 입문.D. 반 노스트랜드, 프린스턴, 뉴저지 주
- Kiefer, J. (1977). "Conditional Confidence Statements and Confidence Estimators (with discussion)". Journal of the American Statistical Association. 72 (360a): 789–827. doi:10.1080/01621459.1977.10479956. JSTOR 2286460.
- Mayo, D. G. (1981) "Neyman-Pearson 이론의 신뢰구간 방어", 과학철학, 48(2), 269-280. JSTOR 187185
- Neyman, J. (1937년) "고전 확률론에 기초한 통계적 추정 이론의 개요" 런던 왕립학회 철학적 거래, 236, 333–380. (세미널 워크)
- Robinson, G.K. (1975). "Some Counterexamples to the Theory of Confidence Intervals". Biometrika. 62 (1): 155–161. doi:10.1093/biomet/62.1.155. JSTOR 2334498.
- 새비지, L. J. (1962), 통계적 추론의 기초.메튜엔, 런던
- Smithson, M. (2003) 신뢰 구간.Social Sciences Series, No.140. Belmont, CA: SAGE 출판물.ISBN 978-0-7619-2499-9.
- Mehta, S. (2014) 통계 토픽 ISBN 978-1-4992-7353-3
- "Confidence estimation", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Morey, R. D.; Hoekstra, R.; Rouder, J. N.; Lee, M. D.; Wagenmakers, E.-J. (2016). "The fallacy of placing confidence in confidence intervals". Psychonomic Bulletin & Review. 23 (1): 103–123. doi:10.3758/s13423-015-0947-8. PMC 4742505. PMID 26450628.
외부 링크
- Excel에서 실행되는 신뢰구간 탐색 소프트웨어 튜토리얼 프로그램
- R-제곱, 회귀 계수 및 회귀 절편에 대한 신뢰 구간 계산기
- Weisstein, Eric W. "Confidence Interval". MathWorld.
- CAUSEweb.org 신뢰구간을 포함한 통계수치를 가르치기 위한 많은 자원.
- 신뢰 구간에 대한 대화형 소개
- 신뢰 구간: Eric Schulz의 신뢰 수준, 표본 크기 및 오차 한계, Wolfram 시연 프로젝트.
- 공중 보건에 대한 신뢰 구간.예를 들어 간단한 설명과 0에 가까운 작은 표본 크기 또는 비율에 대한 처리 방법을 설명합니다.

 신뢰구간을 제공하는 것으로 받아들여질 수 있습니다.
신뢰구간을 제공하는 것으로 받아들여질 수 있습니다.












![{\displaystyle \left[{\bar {x}}-{\frac {cs}{\sqrt {n}}},{\bar {x}}+{\frac {cs}{\sqrt {n}}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02a90d533cc8ae393c6949495405824f49865b80)

 균일한 분포(' - 1/2, ' + 1/2)로부터 독립된 관측치라고 합니다.그러면 최적의 50% 신뢰
균일한 분포(' - 1/2, ' + 1/2)로부터 독립된 관측치라고 합니다.그러면 최적의 50% 신뢰![{\displaystyle {\bar {X}}\pm {\begin{cases}{\dfrac {|X_{1}-X_{2}|}{2}}&{\text{if }}|X_{1}-X_{2}|<1/2\\[8pt]{\dfrac {1-|X_{1}-X_{2}|}{2}}&{\text{if }}|X_{1}-X_{2}|\geq 1/2.\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/80260117bd9ee1f05d0928e0b5697663a297ecbc)








