정규-역-감마 분포

정상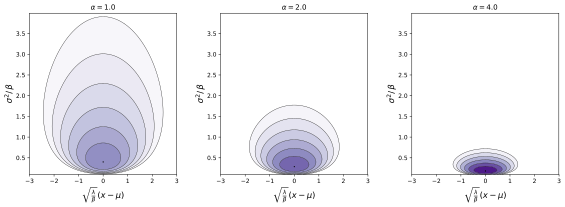의

확률밀도함수
매개변수	$[\$ 위치$$(실제) > ${\$실제) > ${\$ >$0\,}($실제) > ${\$ >0$\,}($실제)
지원	$(-\displaystyle x\in (-\inflt,\in)\,\!,\,\;\fltma ^{2}\in (0,\inflt )}$
PDF	${\displaystyle {\frac {\sqrt {\lambda }}{\sqrt {2\pi \sigma ^{2}}}}{\frac {\beta ^{\alpha }}{\Gamma (\alpha )}}\left({\frac {1}{\sigma ^{2}}}\right)^{\alpha +1}\exp \left(-{\frac {2\beta +\lambda (x-\mu )^{2}}{2\sigma ^{2}}}\right)}$
평균	${\displaystyle \operatorname {E} [x]=\mu }$ ${\displaystyle \mathrm{E}}$ ${\displaystyle }$ [${\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$ ${\displaystyle {}^{}}$= ${\displaystyle \beta \frac{}{}}$ ${\displaystyle \frac{\mathrm{\alpha }}{}}$- 1 ${\$> ${\displaystyalpha >1}$에 대해
모드	${\displaystyle x=\mu \\{\textrm {(univariate)}},x={\mu }\\textrm {(virariate)}}}$ ${\displaystyle \prema ^{2}={\frac {\frac }{\reason +1+1/2}}:},\textrm {(univariate)}}},\frac ^{\frac }{\reason +1+k/2}}:};{\textm(variate)}}}$
분산	${\displaystyle \mathrm{Var}}$ ${\displaystyle }$ [ ${\displaystyle x}$ ${\displaystyle ]}$= ${\displaystyle \beta \frac{}{}}$ ${\displaystyle \frac{(\mathrm{\alpha }}{}}$- 1${\displaystyle \frac{}{}}$) ${\displaystyle \frac{\lambda }{}}$ ${\$ $}}}}},$$$> ${\displaystystyle \alpha >$1} ${\displaystyle }$$Var$${\displaystyle }$ [${\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$ ${\displaystyle {}^{}}$= ${\displaystyle \frac{\beta }{}}$ 2 (${\displaystyle \frac{{}^{}}{\mathrm{\alpha }}}$ ${\displaystyle \frac{-{}^{}}{}}$1 )${\displaystyle \frac{{}^{}{2\mathrm{}}^{}}{}}$ ( ${\displaystyle \frac{\alpha }{}}$ ${\displaystyle \frac{-}{}}$ ${\displaystyle \frac{2}{}}$)$${\$displaystyle$$\operatorname$${Var}[\sigma$^{$2}]={\frac {\fraca$ -1$)}{{2}}:{{{{{{{}}(\$$alpha$ $-1)^{2$$}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}.$ ${\displaystyle }$ [${\displaystyle x}$ , ${\displaystyle {}^{}}$ 2 ] = 0$$ \$operatorname$ {Cov}[$x,\sigma ^{2$}]=0$}, α$> $1$$displaystyle \alpha >1}$의 경우

확률 이론과 통계에서 정규-인버스-감마 분포(또는 가우스-인버스-감마 분포)는 다변량 연속 확률 분포의 4-모수 계열이다.평균과 분산을 알 수 없는 정규 분포 이전의 결합 값이다.null

정의

가정하다

${\displaystyle x\mid \sigma ^{2},\mu,\lambda \sim \mathrmatrix {N}(\mu ,\sigma ^{2}/\lambda )\,\!}$

평균 $\mu {\displaystyle }$ ${\displaystyle \mu }$ 및$$ 분산 and ${\displaystyle {2\mathrm{}}^{}}$ /$${\$displaystyle \displayma ^{2}/\lambda }$을(를$)$ 갖는 정규 분포, 여기서

${\displaystyle \sigma ^{2}\mid \alpha ,\beta \sim \Gamma ^{-1}(\alpha ,\beta )\!}$

역 감마 분포를 가진다.그러면${\displaystyle }$( ${\displaystyle x}$ ,${\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$) ${\displaystyle(x,\sigma ^{2})$에 다음과 같이 표시되는 정규-인버스-감마 분포가 있음$$

${\displaystyle(x,\sigma ^{2})\심(\text{{N-}}\Gamma ^{1}(\mu,\lambda,\alpha,\beta )\!}$

(${\displaystyle \text{NIG}}$ ${\$${\displaystyle \text{N-}}$ ${\displaystyle \gamma {\mathrm{}}^{}}$- ${\displaystyle 1^{}}$. ${\displaystyle {\text{N-}\Gamma ^{-1}}$ 대신 $N-$-}도$$ 사용된다$.$

정규-반복-위샤트 분포는 다변량 랜덤 변수에 대해 정의된 정규-반복-감마 분포의 일반화다.null

특성화

확률밀도함수

${\displaystyle f(x,\sigma ^{2}\mid \mu ,\lambda ,\alpha ,\beta )={\frac {\sqrt {\lambda }}{\sigma {\sqrt {2\pi }}}}\,{\frac {\beta ^{\alpha }}{\Gamma (\alpha )}}\,\left({\frac {1}{\sigma ^{2}}}\right)^{\alpha +1}\exp \left(-{\frac {2\beta +\lambda (x-\mu )^{2}}{2\sigma ^{2}}}\right)}$

$x{\displaystyle \mathbf{}}$ ${\$가) ${\displaystyle \mathrm{k}}$ ${\displaystyle \times }$ 1 ${\displaystyle k\times 1}$ 랜덤$$ 벡터인$$ 다변량 형식의 경우,

${\displaystyle f(\mathbf {x} ,\sigma ^{2}\mid \mu ,\mathbf {V} ^{-1},\alpha ,\beta )= \mathbf {V} ^{-1/2}{(2\pi )^{-k/2}}\,{\frac {\beta ^{\alpha }}{\Gamma (\alpha )}}\,\left({\frac {1}{\sigma ^{2}}}\right)^{\alpha +1+k/2}\exp \left(-{\frac {2\beta +(\mathbf {x} -{\boldsymbol {\mu }})^{T}\mathbf {V} ^{-1}(\mathbf {x} -{\boldsymbol {\mu }})}{2\sigma ^{2}}}\오른쪽).}$

where ${\displaystyle \mathbf {V} }$ is the determinant of the ${\displaystyle k\times k}$ matrix ${\displaystyle \mathbf {V} }$. Note how this last equation reduces to the first form if ${\displaystyle k=1}$ so that ${\displaystyle \mathbf {x} ,\mathbf {V} ,{\boldsymbol {\$$mu }}}$은(는) 스칼라다.null

대체 매개 변수화

$pdf{\displaystyle }$ = 1${\displaystyle }$/${\displaystyle \lambda }$ ${\displaystyle \gamma =1/\lambda }$을(를) 둘 수도 있으며, 이 경우$$ pdf가 된다.

${\displaystyle f(x,\sigma ^{2}\mid \mu ,\gamma ,\alpha ,\beta )={\frac {1}{\sigma {\sqrt {2\pi \gamma }}}}\,{\frac {\beta ^{\alpha }}{\Gamma (\alpha )}}\,\left({\frac {1}{\sigma ^{2}}}\right)^{\alpha +1}\exp \left(-{\frac {2\gamma \beta +(x-\mu )^{2}}{2\gamma \sigma ^{2}}}\right)}$

다변량 형식에서 해당하는 변경은 역 $V{\displaystyle {\mathbf{}}^{}}$- 1 ${\$ 대신$$ 공분산 $행렬{\displaystyle \mathbf{}}$ V ${\$을(를) 매개 변수로$$ 간주하는 것이다.null

누적분포함수

${\displaystyle F(x,\sigma ^{2}\mid \mu ,\lambda ,\alpha ,\beta )={\frac {e^{-{\frac {\beta }{\sigma ^{2}}}}\left({\frac {\beta }{\sigma ^{2}}}\right)^{\alpha }\left(\operatorname {erf} \left({\frac {{\sqrt {\lambda }}(x-\mu )}{{\sqrt {2}}\sigma }}\right)+1\right)}{2\sigma ^{2}\Gamma (\alpha )}}}$

특성.

한계분포

주어진${\displaystyle }$( ${\displaystyle x,}$ ${\displaystyle {\sigma \mathrm{}}^{}}$ 2${\displaystyle {}^{}}$)${\displaystyle }$~ ${\displaystyle {\mathrm{N-}}^{}}$ ${\displaystyle \gamma {\mathrm{}}^{}}$- 1${\displaystyle {}^{}}$(${\displaystyle \mu }$,${\displaystyle \lambda ,}$ ${\displaystyle \alpha ,}$ ${\displaystyle \beta }$)${\displaystyle }$. ${\displaystyle (x,\sigma ^{2})\심(\text{N-}}}}\Gamma ^{1}(\mu,\lambda,\alpha,\ba$ )\ba $)\!$$}}$ 위와 같이$$ $\sigma {\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$ ${\$개$$ 자체로 역 감마 분포를 따른다.

${\displaystyle \sigma ^{2}\심 \Gamma ^{-1}(\alpha ,\beta )\!}$

$\alpha {\displaystyle \sqrt{\frac{}{}}}$ ${\displaystyle \sqrt{\frac{\lambda }{}}}$ ${\displaystyle \sqrt{\frac{(}{}}}$λ +${\displaystyle \sqrt{\frac{}{}}}$1${\displaystyle \sqrt{\frac{}{}}}$) (${\displaystyle \sqrt{\frac{}{}}x}$- ${\displaystyle \mu }$) ${\displaystyle {\sqrt {\frac$ {\$fract \\$fract \\\$fract }}{\da$+$1)}}}}}(x-\mu$)은 t 분포를 따르는 반면$$, 2 ${\displaystyle \alpha }$ ${\displaystytytyle$ $\c$.^[1]

다변량 사례에서 $x{\displaystyle \mathbf{}}$ ${\$의 한계$$ 분포는 다변량 t 분포:

${\displaystyle \mathbf {x} \sim t_{2\alpha }({\boldsymbol {\mu }}},{\frac {\beta }{\alpha }}}\mathbf {V}^-1}!}$

합계

스케일링

지수군

정보 엔트로피

쿨백-라이블러 발산

최대우도 추정

이 구간은 비어 있다.추가하면 도움이 된다.(2010년 7월)

모수의 후방 분포

정상 감마 분포 및 결합에 대한 내용은 이전 항목을 참조하십시오.null

매개변수 해석

정상 감마 분포 및 결합에 대한 내용은 이전 항목을 참조하십시오.null

일반-반전-감마 랜덤 변수 생성

랜덤 변수의 생성은 간단하다.

1. ${\displaystyle {\alpha \mathrm{}}^{}}$ ${\$displaystyle $\sigma ^{$2}} $매개변수$ $\alpha {\displaystyle }$ ${\displaystyle \alpha }$ 및$$ $\beta {\displaystyle }$ ${\displaystyle \beta }}$을(를) 갖는 역 감마 분포로부터 샘플$$ sample 2{\$displaystystyst$
2. 평균 $\mu {\displaystyle }$ ${\displaystyle \mu }$ 및 ${\displaystyle {분산\mathrm{}}^{}}$ and$$ 2 /${\displaystyle {}^{}\lambda }${\$displaystyle \sigma$^{$2}/\lambda }$을(를) 갖는 정규 분포의$$ $표본{\displaystyle }$ x ${\displaystystyle x}$

관련 분포

• 정규 감마 분포는 분산이 아닌 정밀도에 의해 모수화된 분포와 동일하다.
• 다변량 평균과 완전히 알려지지 않은 양의 정의 공분산 행렬 matrix $2{\displaystyle {}^{}}$ ${\displaystyle {}^{}\mathbf{}}$ ${\$을(를) 허용하는 이 분포의 일반화.$$ 여기서 다변량 역감마 분포에서 공분산 행렬은 스케일 계수 ${\displaystyle {factor\mathrm{}}^{}}$ 2 ${\$}까지 알려진 것으로 간주된다.$gma ^{2$}}$)$는 정규-인버스-위샤트 분포다.

참고 항목

• 복합 확률 분포

참조

• Denison, David G. T; Holmes, Christopher C.; Malick, Bani K.; Smith, Adrian F. M. (2002) Bayesian Methods for 비선형 분류 및 회귀 분석, Wiley.ISBN 0471490369
• 코흐, 칼 루돌프(2007) 베이시안 통계 소개(2판), 스프링거.ISBN 354072723X