부품별 통합

미적분학에서, 그리고 더 일반적으로 수학적 분석에서, 부품에 의한 통합이나 부분적 통합은 그 파생상품과 반분제의 생산물의 적분이라는 관점에서 함수의 산물의 적분을 찾는 과정이다. 그것은 기능 산물의 해독제를 용액을 더 쉽게 찾을 수 있는 해독제로 변환하기 위해 자주 사용된다. 그 규칙은 차별화의 제품 규칙의 필수적인 버전이라고 생각할 수 있다.

부품 공식에 의한 통합은 다음과 같다.

Or, letting ${\displaystyle u=u(x)}$ and ${\displaystyle du=u'(x)\,dx}$ while ${\displaystyle v=v(x)}$ and ${\displaystyle dv=v'(x)\,dx}$, the formula can be written more compactly:

수학자 브룩 테일러는 부분별 통합을 발견했고, 1715년에 처음으로 이 아이디어를 발표했다.^[1][2] 리만-스티엘트제스와 르베그-스티엘트제스 통합에는 보다 일반적인 부품별 통합 형식이 존재한다. 시퀀스에 대한 이산 아날로그를 부품별 합계라고 한다.

정리

두 가지 기능의 제품

그 정리는 다음과 같이 도출할 수 있다. u(x)와 v(x)의 두 가지 연속적으로 다른 기능에 대해 제품 규칙은 다음과 같이 명시한다.

양쪽을 x에 대해 통합하고,

그리고 무기한 적분은 해독제라는 것을 알아채고

통합의 상수 글쓰기를 소홀히 하는 곳 이는 부품별 통합 공식을 산출한다.

또는 차등 $d{\displaystyle }$ ${\displaystyle u}$ =${\displaystyle u{}^{}}$u${\displaystyle u}$ = d$$x {\$displaystyle du=u$'(x$)\,$$dx{\displaystyle }$$\},$${\displaystyle d}$ ${\displaystyle {}^{}}$ =${\displaystyle {}^{}}$v${\displaystyle x}$( ${\displaystyle x}$) d$,$ {\$displaystyle dv=v$'(x$)\,dx,\dism }$의 관점에서 dv = u }

이것은 불특정 상수가 양쪽에 추가된 기능의 동일성으로 이해되기 위함이다. 두 값 x = a와 x = b 사이의 각 변의 차이를 취하고 미적분의 기본 정리를 적용하면 다음과 같은 확실한 적분 버전이 나온다.

원래의 적분 uv uv uv uv dx는 파생 v′을 포함하고 있다; 정리를 적용하려면 v'의 반분제인 v를 찾은 다음 결과 적분 ∫뷔 dx를 평가해야 한다.

덜 매끄러운 기능에 대한 유효성

u와 v가 계속 다를 필요는 없다. 부품별 통합은 u가 절대적으로 연속적이고, v′라는 함수가 르베그 통합 가능(그러나 반드시 연속되는 것은 아님)^[3]인 경우에 효과가 있다. (v′가 불연속성을 갖는다면, 그것의 반분해 v는 그 시점에 파생상품을 가지고 있지 않을 수 있다.)

만약 통합의 간격이 작지 않다면, u와 v가 (u와 v가 연속적이고 연속적으로 다른) 몇 가지 예시처럼 전체 간격에서 절대적으로 연속적일 필요가 없다. 예를 들어, 다음과 같다.

u는 [1, ∞] 간격으로 절대적으로 연속되지 않지만, 그럼에도 불구하고

so long as ${\displaystyle \left[u(x)v(x)\right]_{1}^{\infty }}$ is taken to mean the limit of ${\displaystyle u(L)v(L)-u(1)v(1)}$ as ${\displaystyle L\to \infty }$ and so long as the two terms on the right-hand side are finite. $v{\displaystyle }$( ${\displaystyle x}$)${\displaystyle }$=${\displaystyle }$- ${\displaystyle e^{}}$- x${\displaystyle {}^{}}$. ${\displaystyle v(x)=-e^{-x}$를 선택하는 경우에만 해당된다.$}$ 유사한$$ 경우

v′는 [1, ∞] 간격에 따라 르베그 통합이 가능하지 않지만, 그럼에도 불구하고

같은 해석으로

또한 u와 v가 계속 다를 수 없는 비슷한 예를 쉽게 생각해 낼 수 있다.

또한,${\displaystyle }f{\displaystyle }$ (${\displaystyle x}$ )$${\$displaystyle$ f$(x)}$이(가$){\displaystyle }$ 세그먼트 [,${\displaystyle b}$ ${\displaystyle ],}$ ${\displaystyle [a$$,b$$]$ 및$$ $\phi {\displaystyle }$(${\displaystyle x)}$ ${\displaystyle \varphi (x)}$의 경계 변동 함수인 경우, $[,{\displaystyle }$ $b$ ${\displaysty]$에서 서로 다른 기능을$$$$ 사용할 수 있다.

where ${\displaystyle d(\chi _{[a,b]}(x){\widetilde {f}}(x))}$ denotes the signed measure corresponding to the function of bounded variation ${\displaystyle \chi _{[a,b]}(x)f(x)}$, and functions ${\displaystyle {\widetilde {f}},{\widetil$$de {\barphi }}$은(는) $f{\displaystyle }$, ${\displaystyle \phi }$ ${\displaystyle f,\varphi }$을(를) $R{\displaystyle \mathbb{},}$ ${\displaystyle \mathb {R}$까지 확장한 것으로$$, 각각$$ 경계 변동을 가지며 구별이 가능하다.^{[citation needed]}

여러 기능의 제품

u(x), v(x), w(x)의 세 가지 곱한 기능에 대한 제품 규칙을 통합하면 다음과 유사한 결과가 나온다.

일반적으로 n개의 요인에 대해

그 결과로 이어지다

시각화

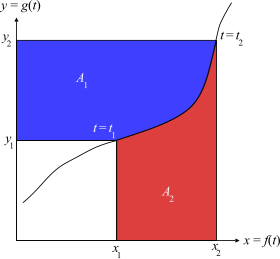
모수 곡선 기준(x, y) = (f(t), g(t))을 고려하십시오. 곡선이 국소적으로 일대일이고 통합이 가능하다고 가정하면, 우리는 정의할 수 있다.

${\displaystyle x(y)=f(g^{-1}(y))}$

${\displaystyle y(x)=g(f^{-1}(x))}$

푸른 지방의 면적은

${\displaystyle A_{1}=\int _{y_{1}^{y_{2}}x(y)\,dy}$

마찬가지로 적색 지역의 면적은

${\displaystyle A_{2}=\int_{x_{1}^{x_{2}}y(x)\,dx}$

총 면적 A₁ + A는₂ 큰 직사각형의 면적 xy에서₂₂ 작은 직사각형의 면적 xy와 동일하다₁₁.

${\displaystyle \overbrace {\int_{y_{1}^{2}}x(y)\,dy}^{A_{1}:{2}}:00+\\{x_{1}}}{x_{1}^{2}}(x)\,dx}^{A_{2}}:\\\\\빅글.}x\cdot y(x){\biggl }_{x_{1}:{1}^{1}^{1}:{2}}\\\\biggl .}y\cdot x(y){\biggl }}{y_}}{1}^{y_{2}}.}$

아니면 t로 따지면

${\displaystyle \int_{t_{1}^{2}}x(t)\,dy(t)+\,dy(t)+\{1}^{1}{{1}y(t)\\\\\biggl .}x(t)y(t)\\\biggl }}{t_{1}{1}}{1}:{2}}:}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

또는, 무기한 통합의 관점에서, 이것은 다음과 같이 쓰여질 수 있다.

$\displaystyle \int x\,dy+\int y\,dx\ =\ xy}$

재배열:

$\displaystyle \int x\,dy\ =\ xy-\int y\,dx}$

따라서 부품별 통합은 직사각형 영역과 적색 영역의 영역에서 청색 영역의 영역을 도출하는 것으로 생각할 수 있다.

또한 이 시각화는 f(x) 함수의 적분을 알 때 부품별 통합이 역함수⁻¹ f(x)의 적분을 찾는 데 도움이 되는 이유를 설명한다. 실제로 함수 x(y)와 y(x)는 inverses이며, 적분 dy x dy는 적분 y y dx를 알고 위와 같이 계산할 수 있다. 특히, 이것은 로그와 역삼각계 함수를 통합하기 위한 부품별 통합의 사용을 설명한다. 실제로 $f{\displaystyle }$ ${\displaystyle f}$이(가) 간격마다 다른 일대일 함수인 경우, 부품별 통합을 사용하여 ${\displaystyle {\mathrm{f}}^{}}$ ${\$ f$^{-1}$의 적분 공식을 f${\displaystyle {}^{}}$${\displaystyle f$의 적분 측면에서 도출할 수 있다. 이것은 역함수의 적분이라는 글에서 증명된다.

적용들

해독제 찾기

부품별 통합은 통합을 해결하기 위한 순수 기계적인 과정이 아니라 경험적 접근법이다. 통합하기 위한 단일 함수를 감안할 때, 일반적인 전략은 이 단일 함수를 두 함수의 제품으로 조심스럽게 분리하여 부품 공식에 의한 통합의 잔여 적분을 평가하기 쉽도록 하는 것이다(x(x)v(x)제 기능을 하다 다음 양식은 취할 수 있는 최선의 전략을 설명하는 데 유용하다.

$\displaystyle \int uv\dx=u\int v\dx-\int \왼쪽(u'\int v\dx\right)\dx.}$

오른쪽은 u를 구분하여 v를 통합하므로, u를 구별할 때 단순화하는 기능으로 선택하거나, 통합할 때 단순화하는 기능으로 v를 선택하는 것이 유용하다. 간단한 예로 다음을 고려하십시오.

${\displaystyle \int{\frac {\ln(x)}{x^{2}}\dx\ .}$

ln(x)의 파생상품은 다음과 같기 때문에 1/x, part u를 만든다(ln(x) part u; 1/x의² 해독제가 -1/x이므로² 1/xdx part dv를 만든다. 이 공식은 이제 다음을 산출한다.

${\displaystyle \int{\frac {\ln(x)}{x^{2}}:\dx=-{\frac {1}{x}}}{\biggl (}{\frac {1}{x}}{\biggr )}{\biggl (}-{x}{x}}}.x\x\}.$

-1/x의² 해독제는 전원 규칙으로 찾을 수 있으며 1/x이다.

또는 제품 u′(∫v dx)이 취소로 인해 단순화되도록 u와 v를 선택할 수 있다. 예를 들어, 다음과 같이 통합하고자 한다고 가정합시다.

${\displaystyle \int \sec ^{2}(x)\cdot \ln {\Bigl }\sin(x){\Bigr }}\dx.}$

u(x) = ln(sin(x) ) 및 v(x) = secx를² 선택하면 체인 규칙을 사용하여 1/tan x로 구별되고 v는 tann x에 통합되므로 공식은 다음을 제공한다.

${\displaystyle \int \sec ^{2}(x)\cdot \ln {\Big (}{\bigl }\sin(x){\bigr }{\Big )}\ dx=\tan(x)\cdot \ln {\Big (}{\bigl }\sin(x){\bigr }{\Big )}-\int \tan(x)\cdot {\frac {1}{\tan(x)}}\,dx\ .}$

통합과 단순화는 1로 단순화되므로 해독제는 x이다. 단순화 조합을 찾는 것은 종종 실험을 수반한다.

일부 응용 프로그램에서는 부품별 통합에 의해 생산된 적분이 단순한 형태를 갖도록 보장할 필요가 없을 수 있다. 예를 들어, 수치 분석에서는 크기가 작아서 작은 오차항만 기여하는 것으로 충분할 수 있다. 다른 특별한 기법들은 아래의 예에서 설명된다.

다항식 및 삼각함수

계산하기 위해

${\displaystyle I=\int x\cos(x)\dx\ ,}$

허용:

${\displaystyle u=x\ \Rightarrow \ du=dx}$

${\displaystyle dv=\cos(x)\dx\\Rightarrow \v=\int \cos(x)\dx=\sin(x)}$

다음:

${\displaystyle {\begin}\int x\cos(x)\dx&=\int u\&=cdot v-\int v-\int v-\int v-\int v\du\&=x(x)-int \x\x(x)+C, ended{aged}}$

여기서 C는 통합의 상수다.

폼에 있는 x의 상위 파워용

${\displaystyle \int x^{n}e^{x}\x,\\int x^{n}\sin(x)\x,\int x^{n}\cos(x)\dx\,}$

부품에 의한 통합을 반복적으로 사용하는 것은 이것과 같은 통합을 평가할 수 있다; 정리의 각 적용은 x의 힘을 하나씩 떨어뜨린다.

지수 및 삼각 함수

부품별 통합의 작업을 조사하기 위해 일반적으로 사용되는 예는 다음과 같다.

${\displaystyle I=\int e^{x}\cos(x)\dx.}$

여기서는 부품별 통합을 두 번 실시한다. 먼저 하자

$\displaystyle u=\cos(x)\ \Rightarrow \du=-\sin(x)\dx}$

${\displaystyle dv=e^{x}\dx\\Rightarrow \ v=\int e^{x}\dx=e^{x}}}$

다음:

${\displaystyle \int e^{x}\cos(x)\dx=e^{x}\cos(x)+\int e^{x}\sin(x)\dx.}$

이제, 나머지 적분을 평가하기 위해 우리는 다음과 같은 부품별 통합을 다시 사용한다.

$\displaystyle u=\sin(x)\ \Rightarrow \du=\cos(x)\dx}$

${\displaystyle dv=e^{x}\dx\\Rightarrow \ v=\int e^{x}\dx=e^{x}.}$

다음:

${\displaystyle \int e^{x}\sin(x)\dx=e^{x}\sin(x)-\int e^{x}\cos(x)\dx.}$

이것들을 종합해 보면

${\displaystyle \int e^{x}\cos(x)\dx=e^{x}\cos(x)+e^{x}\sin(x)-\int e^{x}\cos(x)\dx.}$

이 방정식의 양면에는 동일한 적분이 나타난다. 통합은 단순히 양쪽에 추가되어

${\displaystyle 2\int e^{x}\dx=e^{x}{\bigl [}\sin(x)+\cos(x){\bigr ]}+C,}$

로 재배열되는.

${\displaystyle \int e^{x}\cos(x)\dx={\frac {1}{1}{1}e^{1}{x}{\bigl [}\sin(x)+\cos(x){\bigr ]}+C'}}$

여기서 다시 C(및 C′ = C/2)는 통합의 상수다.

이와 유사한 방법을 사용하여 차등 입자의 적분을 찾는다.

함수에 일치를 곱함

다른 잘 알려진 두 가지 예는 부품에 의한 통합이 1과 그 자체로 표현된 함수에 적용되는 경우다. 이것은 함수의 파생상품이 알려져 있고, 이 파생상품 타임즈 x의 적분 또한 알려져 있는 경우에 작용한다.

첫 번째 예는 ∫ ln(x) dx이다. 이를 다음과 같이 기록한다.

$\displaystyle I=\int \ln(x)\cdot 1\dx\ .}$

허용:

${\displaystyle u=\ln(x)\\Rightarrow \du={\frac {dx}{x}}}}$

${\displaystyle dv=dx\ \Rightarrow \ v=x}$

다음:

${\displaystyle {\begin{aigned}\int \ln(x)\dx&=x\ln(x)-int {\frac {x}\x\&#x(x)-int 1\dx\&=ln(x)-x+C\end{aigned}}}}}}}}}$

여기서 C는 통합의 상수다.

두 번째 예는 역 접선 함수 아크탄(x):

$\displaystyle I=\int \arctan(x)\dx.}$

로 다시 쓰십시오.

$\displaystyle \int \arctan(x)\cdot 1\dx.}$

이제 다음 작업을 수행하십시오.

${\displaystyle u=\arctan(x)\ \Rightarrow \du={\frac {dx}{1+x^{2}}}}$

${\displaystyle dv=dx\ \Rightarrow \ v=x}$

그때

${\displaystyle {\regated}\int \arctan(x)\x&=x\arctan(x)-\int {\frac {x}{1+x^{2}}}\dx\\[8pt]&=x\arctan(x)-{\frac {\ln(1+x^{2}}{2}}+C\end}}}}}$

역사슬 규칙 방법과 자연 로그 적분 조건의 조합 사용.

LIATE 규칙

u로서 다음 목록에서 먼저 오는 기능을 선택하는 것으로 구성되는 경험칙이 제안되었다.^[4]

L$$ – 로그 함수: ${\displaystyle \ln }$ ${\displaystyle }$( ${\displaystyle x}$)${\displaystyle }$, ${\displaystyle {\log }_{}}$ ${\displaystyle b_{}}$ ${\displaystyle {}_{}}$( ${\displaystyle x}$)${\displaystyle }$, ${\displaystyle \ln(x),\log _{b}(x),}$ 등

I – 역삼각 함수(중복 아날로그 포함): ${\displaystyle \arctan x}$ ${\displaystyle (}$ x )${\displaystyle }$, ${\displaystyle \mathrm{arcsec},}$( ${\displaystyle x}$ ) , ${\displaystyle \mathrm{arsinh}}$ ${\displaystyle }$( ${\displaystyle x}$)${\displaystyle }$, ${\displaystyle \arctan(x),\ \operatorname {arcsec}(x$),$\operatorname {arsinh}(x),$ }, } 등$$.

A$$ – 대수 함수: ${\displaystyle {x\mathrm{}}^{}}$ $2{\displaystyle {}^{}}$,${\displaystyle {}^{}}$3 ${\displaystyle {}^{}}$ ${\displaystyle {50}^{}}$ ${\displaystyle$ x$^{2},\ 3x^{50}$ 등

T – 삼각 함수( 쌍곡 아날로그 ${\displaystyle \mathrm{포함}}$): ${\displaystyle \sin }$ ${\displaystyle }$( x${\displaystyle }$)${\displaystyle }$, ${\displaystyle \tan }$ ${\displaystyle }$( ${\displaystyle x}$)${\displaystyle }$, ${\displaystyle \mathrm{secch}}$ ${\displaystyle }$( x${\displaystyle }$)${\displaystyle }$, ${\displaystyle \sin(x),\tan(x),\\\ \operatorname {sech}$ ($x),}$ 등$$.

E$$ – 지수 함수: $e{\displaystyle {}^{}}$ ${\displaystyle x^{}}$ ${\displaystyle {}^{}}$ ${\displaystyle {19}^{}}$ x ,${\displaystyle$ e$^{x},\ 19^{x},}$ 등

dv가 될 기능은 목록에서 가장 마지막에 나오는 것이다. 그 이유는 리스트에서 낮은 기능들은 일반적으로 그 위에 있는 기능들보다 해독 작용이 더 쉽기 때문이다. 규칙은 D가 dv를 의미하고 목록의 맨 위는 dv로 선택한 함수인 "DETAIL"로 기록되기도 한다.

LIATE 규칙을 시연하려면 통합 요소를 고려하십시오.

${\displaystyle \int x\cdot \cos(x)\,dx.}$

LIATE 규칙에 따라 u = x, dv = cos(x) dx, 따라서 du = dx, v = sin(x)은 적분이 된다.

${\displaystyle x\cdot \sin(x)-\int 1\sin(x)\,dx,}$

어느 것이 같은가.

$\displaystyle x\cdot \sin(x)+\cos(x)+C.}$

일반적으로 u를 선택하려고 하며 dv는 u보다 단순하고 dv는 통합하기 쉽다. 대신 cos(x)가 u로, x dx가 dv로 선택되었다면, 우리는 그 일체형(integrated)을 가질 것이다.

${\displaystyle {\frac{x^{2}}:\cos(x)+\int {\frac{x^{2}}:\sin(x)\,dx,}$

부품 공식에 의한 통합의 재귀적 적용 후, 무한 재귀가 발생하여 아무 곳에서도 이어질 수 없다.

유용한 경험 법칙이긴 하지만 LIATE 규칙에는 예외가 있다. 일반적인 대안은 "ILATE" 순서의 규칙을 대신 고려하는 것이다. 또한 경우에 따라서는 다항어를 비종교적인 방법으로 분할할 필요가 있다. 예를 들어, 통합하기 위해

${\displaystyle \int x^{3}e^{x^{2}}\,dx,}$

정했을 것이다

${\displaystyle u=x^{2},\dv=x\cdot e^{x^{2}}\,dx,}$

하도록

${\displaystyle du=2x\,dx,\frac v={\frac {e^{x^{2}}:{2}.}$

그러면

${\displaystyle \int x^{3}e^{x^{2}}\,dx=\int \left(x^{2}\right)\left(xe^{x^{2}}\right)\,dx=\int u\,dv=uv-\int v\,du={\frac {x^{2}e^{x^{2}}}{2}}-\int xe^{x^{2}}\,dx.}$

마지막으로, 이 결과는 다음과 같다.

${\displaystyle \int x^{3}e^{x^{2}}\,dx={\frac {e^{x^{2}}\왼쪽(x^{2}-1\오른쪽){2}}+C.}$

부품별 통합은 수학 분석에서 이론들을 증명하는 도구로 자주 사용된다.

월리스 제품

$Wallis{\displaystyle }$무한 $제품$({\displaystyle $\pi })$

${\displaystyle {\begin{aligned}{\frac {\pi }{2}}&=\prod _{n=1}^{\infty }{\frac {4n^{2}}{4n^{2}-1}}=\prod _{n=1}^{\infty }\left({\frac {2n}{2n-1}}\cdot {\frac {2n}{2n+1}}\right)\\[6pt]&={\Big (}{\frac {2}{1}}\cdot {\frac {2}{3}}{\Big )}\cdot {\Big (}{\frac {4}{3}}\cdot {\frac {4}{5}}{\Big )}\cdot {\Big (}{\frac {6}{5}}\cdot {\frac {6}{7}}{\Big )}\cdot {\Big (}{\frac {8}{7}}\cdot {\frac {8}{9}}{\Big )}\cdot \;\cdots \end{aligned}}}$

부품에 의한 통합을 이용하여 도출할 수 있다.

감마함수정체

감마 함수는 > 0 ${\displaystyle z>0}$에 대한 부적절한 적분으로 정의되는 특수 함수의 예로서 부품별 통합은 이를 요인 함수의 확장으로 나타낸다.

${\displaystyle {\begin{aigned}\감마(z)&=\int_{0}^{0}{-x^{-x-1}x-1\[6pt]&=-\int_{0}^{0}{}^{}x-1}\,d(e^{-x}\오른쪽)\\[6pt]&=-{\Biggl [}e^{-x}x^{z-1}{\biggl ]{0}^{0}{\int _{0}^{0}^{-x}d\ft(x^{z-1}\right)\\\\\\\\\\[6pt]&=0+\int _{0}^{\infit }\왼쪽(z-1\right)x^{z-2}e^{-}dx\\[6pt]&=z-1(z-1)\감마(z-1)\end{정렬}}}$

이후

${\displaystyle \Gamma(1)=\int_{0}^{\\e^{-x}\,dx=1,}$

$z{\displaystyle }$ ${\displaystyle z}$이(가) 자연수인 경우, $즉{\displaystyle }$ z${\displaystyle }$= ${\displaystyle n\mathbb{}}$ ${\displaystyle \in }$ N ${\$ {$N$ 이 공식을 반복적으로 ${\displaystyle \mathrm{적용}}$하면 :(${\displaystyle n}$+ ${\displaystyle 1}$)${\displaystyle =}$ n${\displaystyle !}$ ${\displaysty \Gamma(n+1)=n!$$}$

조화 분석에 사용

부품별 통합은 조화 분석, 특히 푸리에 분석에서 충분히 부드러운 통합으로 빠르게 진동을 하는 통합이 빠르게 붕괴한다는 것을 보여주기 위해 종종 사용된다. 이것의 가장 일반적인 예는 기능 푸리에 변환의 붕괴가 아래에 설명된 대로 그 기능의 부드러움에 달려 있다는 것을 보여주는 그것의 사용이다.

푸리에 변환 파생 모델

만약 f가 k-time 연속적으로 다른 함수이고 k번째 함수까지의 모든 파생상품이 무한대에서 0으로 붕괴한다면, 그것의 푸리에 변환은 만족한다.

${\displaystyle({\mathcal{F}f^{(k)})(\xi)=(2\pi i\xi )^{k}{\mathcal {F}f(\xi ),}$

여기서 f는^(k) f.의 k번째 파생상품이다(우리의 정확한 상수는 사용되는 푸리에 변환의 관례에 따라 달라진다). 라는 점에 주목함으로써 이를 증명한다.

${\displaystyle {\frac {d}{dy}e^{-2\pi iy\xi}=-2\pi e^{-2\pi iy\xi}}}$

Fourier 변환의 부품별 통합을 통해

${\displaystyle{\begin{정렬}({\mathcal{F}}f')(\xi)&,=\int _ᆲ^ᆳe^ᆴf'(y)\,dy\\&, =\left[e^{-2\pi iy\xi}f(y)\right]_{-\infty}^{\infty}-\int _ᆷ^ᆸᆮfᆯ\,dy\\[5pt]&, =2\pii\xi \int _ᆹ^ᆺe^ᆻfᆰ\,dy\\[5pt]&, =2\pi i\xi{{F\mathcal}}f(.\xi cm이다.\end{정렬}}}$

이 인덕티브를 적용하면 일반 k에 대한 결과가 나온다. 유사한 방법을 사용하여 함수의 파생상품의 라플라스 변환을 찾을 수 있다.

푸리에 변환의 붕괴

위의 결과는 F와 F가^(k) 통합될 수 있다면 F와 F가 통합될 수 있기 때문에 푸리에 변환의 붕괴에 대해 말해준다.

${\displaystyle \vert {\mathcal {F}}f(\xi )\vert \leq {\frac {I(f)}{1+\vert 2\pi \xi \vert ^{k}}},{\text{ where }}I(f)=\int _{-\infty }^{\infty }{\Bigl (}\vert f(y)\vert +\vert f^{(k)}(y)\vert {\Bigr )}\,dy.}$

즉, f가 이러한 조건을 만족하면 푸리에 변환은 적어도 1/ ξ만큼 빠르게 무한대로 분해된다. 특히, k ≥ 2이면 푸리에 변환은 통합이 가능하다.

그 증거는 푸리에 변혁의 정의에서 바로 나온 이 사실을 다음과 같이 사용한다.

${\displaystyle \vert {\mathcal {F}f(\xi )\vert \leq \int _{-\nft }^{\nft }\vert f(y)\vert \dy.}$

이 하위 섹션의 시작 부분에 명시된 동등성에 대해 동일한 아이디어를 사용하는 것은 다음과 같다.

${\displaystyle \vert (2\pi i\xi )^{\mathcal {F}f(\xi )\vert \leq \int_{-\infit }^{\inft }\vert f^{(k)(y)\vert;dy,dy.}$

이 두 불평등을 합산한 다음 1 + 2 ξ로^k 나누면 명시된 불평등이 나타난다.

연산자 이론에서 사용

연산자 이론에서 부품에 의한 통합의 한 가지 용도는 -∆(여기서 ∆은 라플라스 연산자)이 L에² 대한 양성 연산자임을 보여주는 것이다(L^p 공간 참조). 그때 f가 매끄럽고 압축적으로 지원된다면, 부품별 통합을 통해 우리는

${\displaystyle {\begin{aligned}\langle -\Delta f,f\rangle _{L^{2}}&=-\int _{-\infty }^{\infty }f''(x){\overline {f(x)}}\,dx\\[5pt]&=-\left[f'(x){\overline {f(x)}}\right]_{-\infty }^{\infty }+\int _{-\infty }^{\infty }f'(x){\overline {f'(x)}}\,dx\\[5pt]&=\int _{-\infit }^{\infit }\vert f'(x)\vert ^{2}\,dx\geq 0.\end{정렬}}}$

기타 응용 프로그램

• 스터름-리우빌 이론의 경계 조건 결정
• 변동 미적분에서 오일러-라그랑주 방정식 도출

부품별 반복적인 통합

부분 통합 공식의 LHS 적분에서 $v$ ${\displaystyle v}$의 두 번째 파생 모델을 고려하면 RHS 적분:

$\dx=UV'\,dx=uv-\int uv\,dx=uv-\왼쪽(u'v-\int u'v\,dx\right)}$

이러한 반복적인 부분적 통합의 개념을 정도 n의 파생상품으로 확장하면 다음과 같은 결과를 얻을 수 있다.

${\displaystyle {\begin{aligned}\int u^{(0)}v^{(n)}\,dx&=u^{(0)}v^{(n-1)}-u^{(1)}v^{(n-2)}+u^{(2)}v^{(n-3)}-\cdots +(-1)^{n-1}u^{(n-1)}v^{(0)}+(-1)^{n}\int u^{(n)}v^{(0)}\,dx.\\[5pt]&=\sum _{k=0}^{n-1(-1)^{k^{k^{{k}v^{(n-1-k)}+(-1)^{n}\int u^{{n)v^{(0)\dx.\end{정렬}}}$

$이{\displaystyle {}^{}}$ 개념은 v${\displaystyle {}^{}}$($){\$ v$^{(n)}}$의 연속적인 통합을 쉽게 구할 수 있을$$ 때(예: 라플라스틱 또는 푸리에 변환에서처럼 일반 지수 또는 사인 및 코사인)와 $u{\displaystyle }$ ${\displaysty u}$의 n번째 파생형이 소멸할$$ 때$({\displaystyle \mathrm{예}}$: n${\displaystyle }$- 1${\displaystyle }$) ${\displayst$.$yle (n-1)}$ $$. 후자의 조건은 RHS 통합이 사라지기 때문에 부분 통합의 반복을 중단한다.

위의 부분적 통합의 반복 과정에서 통합은

${\displaystyle \int u^{(0)}v^{(n)}\,dx\quad }$ and ${\displaystyle \quad \int u^{(\ell )}v^{(n-\ell )}\,dx\quad }$ and ${\displaystyle \quad \int u^{(m)}v^{(n-m)}\,dx\quad {\text{ for }}1\leq m,\ell \leq$$n}$

친척이 되다 이는 통합체 내$$ $v{\displaystyle }$ ${\displaystyle v}$과 $u{\displaystyle }$ ${\displaystyle u}$ 사이의 파생상품을 임의로 "전환"하는 것으로 해석될 수 있으며, 유용하다는 것도 입증된다(로드게스의 공식 참조).

부품별 표 통합

위의 공식의 필수 과정은 표에 요약할 수 있다; 그 결과의 방법은 "표적 통합"^[5]이라고 불리며 영화 "표적 통합"에 실렸다.^[6]

예를 들어, 적분을 고려하십시오.

${\displaystyle \int }$ ${\displaystyle {}^{}}$ ${\displaystyle {3\mathrm{}}^{}}$ ${\displaystyle \cos }$ ${\displaystyle }$ x ${\displaystyle x}$ x$\$ x$^{3}\cos$ x$\,dx\property }$을${\displaystyle {(}^{}}$를) 가져가고${\displaystyle {\mathrm{u}}^{}}$ =${\displaystyle {}^{}{x\mathrm{}}^{}}$ 3,${\displaystyle {}^{}v{}^{}}$(${\displaystyle n^{}}$) = ${\displaystyle \cos }$ x ${\displaystyle x}$ x${\displaystyle .}${\$displaystyle \^{0}=x^{3},\cos v^{n}=\cos$ x$.}$

$u{\displaystyle {}^{}}$ (${\displaystyle 0^{}}$)${\displaystyle {}^{}}$= ${\displaystyle {}^{}}$ ${\displaystyle {3\mathrm{}}^{}}$ ${\$ 및 그 이후의$$ 파생상품 $u{\displaystyle {}^{}}$($){\$을 0에 도달할 때까지$$ 열거하기 시작하십시오. 그런 다음 열 B의 크기가 A 열과 같을 때까지$$ 함수 $v{\displaystyle {}^{(n}}$ ${\displaystyle {)}^{}}$= ${\displaystyle \cos }$ × ${\displaystyle v^{(n)}=\cos$ x$}$와 그 이후의$$ 통합 v($n{\displaystyle {}^{}}$ ${\displaystyle {-i}^{}}$ )$($n - i ){\$displaystystyle$ v^{($n-i)}}}}}$을 열 B에 나열하십시오. 그 결과는 다음과 같다.

# I	서명	A: 파생상품 u(i)	B: 통합(n−i) v
0	+	${\displaystyle x^{3}}$	$\displaystyle \cos x}$
1	−	${\displaystyle 3x^{2}}$	$\displaystyle \sin x}$
2	+	$6x6x}$	$-\cos x}$
3	−	${\displaystyle 6}$	$-\sin x}$
4	+	${\displaystyle 0}$	$\displaystyle \cos x}$

A열과 B열의 i열 항목과 각 부호는 부품별로 반복적으로 통합되는 과정에서 i단계의 관련 통합을 제공한다. 단계 i = 0은 원래 적분을 산출한다. For the complete result in step i > 0 the ith integral must be added to all the previous products (0 ≤ j < i) of the jth entry of column A and the (j + 1)st entry of column B (i.e., multiply the 1st entry of column A with the 2nd entry of column B, the 2nd entry of column A with the 3rd entry of column B, etc. ...) with the given jth sign. 이 과정은 적분을 산출하는 제품이 0일 때(예의 i = 4) 자연적으로 중단된다. 전체 결과는 다음과 같다(각 항에 교대 기호가 있음).

${\displaystyle \underbrace {(+1)(x^{3})(\sin x)} _{j=0}+\underbrace {(-1)(3x^{2})(-\cos x)} _{j=1}+\underbrace {(+1)(6x)(-\sin x)} _{j=2}+\underbrace {(-1)(6)(\cos x)} _{j=3}+\underbrace {\int (+1)(0)(\cos x)\,dx} _{i=4:\;\to \;C}.}$

이것은 생산된다.

${\displaystyle \underbrace {\int x^{3}\cos x\,dx} _{\text{0}=x^{3}\sin x+3x^{2.}}\cos x-6x\sin x-6\cos x+C.}$

반복적인 부분 통합은 기능 $u{\displaystyle {}^{}}$($){\$과 v${\displaystyle {}^{}}$(${\displaystyle n^{}}$ ${\displaystyle {-}^{}}$ i$){\$을 각각 차별화하고 통합하는 과정에서 제품이 원래$$ 통합의 배수로 나타날 때 유용하게 나타난다. 이 경우 반복은 또한 이 지수 i로 종료될 수 있다.이것은 예상대로 지수함수와 삼각함수로 일어날 수 있다. 예를 들면 다음과 같다.

${\displaystyle \int e^{x}\cos x\,dx.}$

# I	서명	A: 파생상품 u(i)	B: 통합(n−i) v
0	+	${\displaystyle e^{x}}$	$\displaystyle \cos x}$
1	−	${\displaystyle e^{x}}$	$\displaystyle \sin x}$
2	+	${\displaystyle e^{x}}$	$-\cos x}$

이 경우, 지수 i = 2에 대한 적절한 기호가 있는 열 A와 B의 항의 곱은 원래 통합의 음을 산출한다(compare row i = 0, i = 2).

${\displaystyle \underbrace {\int e^{x}\cos x\,dx} _{\text{step 0}}=\underbrace {(+1)(e^{x})(\sin x)} _{j=0}+\underbrace {(-1)(e^{x})(-\cos x)} _{j=1}+\underbrace {\int (+1)(e^{x})(-\cos x)\,dx} _{i=2}.}$

RHS의 적분자가 자체적인$$적분 $display${\$displaystyle$ C$'}$을$($를) 가질 수 있음을 관찰하고 추상 적분을 반대편에 가져오는 것은 다음과 같은 효과를 준다.

${\displaystyle 2\int e^{x}\cos x\,dx=e^{x}\sin x+e^{x}\cos x+C',}$

마지막으로,

${\displaystyle \int e^{x}\cos x\,dx={\frac {1}{1}:{2}}\왼쪽(e^{x})(\sin x+\cos x)\오른쪽)+C,}$

여기서 C = C′/2.

상위 치수

부품별 통합은 적절한 제품 규칙에 미적분학의 기본 정리 버전을 적용함으로써 여러 변수의 함수로 확장할 수 있다. 다변량 미적분학에는 스칼라 값 함수 u와 벡터 값 함수(벡터 필드) V를 포함하는 여러 쌍이 가능하다.^[7]

다양성에 대한 제품 규칙은 다음과 같다.

Suppose ${\displaystyle \Omega }$ is an open bounded subset of ${\displaystyle \mathbb {R} ^{n}}$ with a piecewise smooth boundary ${\displaystyle \Gamma =\partial \Omega }$. Integrating over ${\displaystyle \Omega }$ with respect to the standard volume form ${\displaystyle d\Omega }$, and app다양성 정리를 하는 것은 다음을 제공한다.

여기서 n ${\displaystyle \stackrel{}{}}$ ${\$은(는) 경계로의 외부 단위 정규 벡터로서$$, 표준 리만 볼륨 형식 $d{\displaystyle }$ ${\displaystyle \mathrm{\gamma }}$ ${\displaystyle d\Gamma$}과(는$)$에 대해 통합된다$.$ 재배열은 다음을 제공한다.

또는 다시 말하면

정리의 규칙성 요건은 완화할 수 있다. 예를 들어 경계 $\gamma {\displaystyle \mathrm{}}$= ${\displaystyle \mathrm{\partial }}$ ${\displaystyle \mathrm{\Omega }}$ ${\displaystyle \Gamma =\partial \Oomega}$은(는) 립스키츠 연속형이어야 하며$$, 함수 u, v는 Sobolev spaceH¹(Ω)에만 있어야 한다.

그린의 첫 번째 정체성

Consider the continuously differentiable vector fields ${\displaystyle \mathbf {U} =u_{1}\mathbf {e} _{1}+\cdots +u_{n}\mathbf {e} _{n}}$ and ${\displaystyle v\mathbf {e} _{1},\ldots ,v\mathbf {e} _{n}}$, where ${\displaystyle \mathbf {e} _{i}}$$$$i{\displaystyle }$= ${\displaystyle 1}$, …${\displaystyle }$, ${\displaystyle i=1,\ldots,n}$에 대한 i번째 표준 기준 벡터$.$ 이제 위의 통합을 각 ${\displaystyle {}_{}}$ ${\displaystyle i_{}}$ ${\$ 배$$ 벡터 필드 v e ${\$에 적용하십시오$.$

i를 요약하면 부품 공식에 의한 새로운 통합:

사례 $U{\displaystyle \mathbf{}}$= ${\displaystyle \mathrm{\nabla }}$ ${\displaystyle u}$ ${\displaystyle \mathbf {U} =\nabla u$ 여기서 $u{\displaystyle }$ ${\displaystyle {C2\mathrm{}}^{}(}$Ω${\displaystyle \omega \stackrel{)}{\mathrm{}}}$ ${\displaysty u\in C^{2}({\bar{\$bar {\\\$Oomega}})}$은$$Green의 첫 번째 ID로 알려져 있다.

참고 항목

• Lebesgue-Stieltjes 일체형 부품별 통합
• 2차 공분산을 포함하는 반마분율(semimartingales)을 위한 부품별 통합.
• 대체에 의한 통합
• 레전드르 변환

메모들

추가 읽기

• Louis Brand (10 October 2013). Advanced Calculus: An Introduction to Classical Analysis. Courier Corporation. pp. 267–. ISBN 978-0-486-15799-3.
• Hoffmann, Laurence D.; Bradley, Gerald L. (2004). Calculus for Business, Economics, and the Social and Life Sciences (8th ed.). pp. 450–464. ISBN 0-07-242432-X.
• Willard, Stephen (1976). Calculus and its Applications. Boston: Prindle, Weber & Schmidt. pp. 193–214. ISBN 0-87150-203-8.
• Washington, Allyn J. (1966). Technical Calculus with Analytic Geometry. Reading: Addison-Wesley. pp. 218–245. ISBN 0-8465-8603-7.

외부 링크

• "Integration by parts", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• 부품별 통합—MathWorld의