선형 회귀

시리즈의 일부
회귀 분석
모델
선형 회귀 단순 회귀 다항식 회귀 분석 일반 선형 모형
일반화 선형 모형 개별 선택 이항 회귀 분석 이항 회귀 로지스틱 회귀 분석 다항 로지스틱 회귀 분석 혼합 로짓 프로빗 다항 프로빗 주문된 로짓 순서 프로빗 포아송
다단계 모형 고정 효과 랜덤 효과 선형 혼합 효과 모형 비선형 혼합 효과 모형
비선형 회귀 분석 비모수 반파라메트릭 견고. 양분위수 아이소토닉 주요 컴포넌트 최소 각도 현지의 세그먼트화
변수 오류
견적
최소 제곱 선형 비선형
보통의 가중치 일반화
부분적 총 음이 아닌 능선 회귀 정규화
최소 절대 편차 반복 재중량화 베이지안 베이지안 다변량 최소 제곱 스펙트럼 분석
배경
회귀 검증 평균 및 예측 반응 오차 및 잔차 적합도 학생화 잔차 가우스-마르코프 정리
수학 포털
v t

통계학에서 선형 회귀는 스칼라 반응과 하나 이상의 설명 변수(의존 및 독립 변수라고도 함) 사이의 관계를 모델링하기 위한 선형 접근법이다.하나의 설명 변수가 있는 경우를 단순 선형 회귀 분석이라고 하며, 둘 이상의 설명 변수의 경우 공정을 다중 선형 ^[1]회귀 분석이라고 합니다.이 항은 단일 스칼라 ^[2]변수가 아니라 여러 상관 종속 변수가 예측되는 다변량 선형 회귀 분석과는 다릅니다.

선형 회귀 분석에서 관계는 데이터에서 알 수 없는 모형 모수가 추정되는 선형 예측 변수 함수를 사용하여 모형화됩니다.이러한 모델을 선형 ^[3]모형이라고 합니다.가장 일반적으로 설명 변수(또는 예측 변수)의 값이 주어진 반응의 조건부 평균은 이러한 값의 아핀 함수로 가정되며, 조건부 중위수 또는 일부 다른 분위수가 사용된다.모든 형태의 회귀 분석과 마찬가지로 선형 회귀 분석도 다변량 분석 영역인 모든 변수의 공동 확률 분포보다는 예측 변수 값이 주어진 반응의 조건부 확률 분포에 초점을 맞춥니다.

선형 회귀는 엄격하게 연구되고 실제 응용 ^[4]분야에서 광범위하게 사용된 최초의 회귀 분석 유형이었다.이는 알려지지 않은 모수에 선형적으로 의존하는 모형이 모수와 비선형적으로 관련된 모형보다 적합하기 쉽고 결과 추정치의 통계적 특성을 결정하기 쉽기 때문입니다.

선형 회귀 분석에는 여러 가지 실용적인 용도가 있습니다.대부분의 애플리케이션은 다음의 2개의 큰 카테고리 중 하나로 분류됩니다.

• 예측, 예측 또는 오차 ^{[clarification needed]}감소가 목적인 경우 선형 회귀 분석을 사용하여 예측 모형을 반응 변수 및 설명 변수의 관측된 데이터 집합에 적합시킬 수 있습니다.이러한 모델을 개발한 후, 부수되는 반응 값 없이 설명 변수의 추가 값을 수집하면 적합 모델을 사용하여 반응을 예측할 수 있다.
• 만약 목적이 설명 변수의 변동에 기인할 수 있는 반응 변수의 변동을 설명하는 것이라면, 선형 회귀 분석을 적용하여 반응 변수와 설명 변수 사이의 관계의 강도를 정량화할 수 있으며, 특히 일부 설명 변수가 선형 변수를 가지지 않을 수 있는지 여부를 결정할 수 있다.응답과의 관계를 확인하거나 설명 변수의 어떤 하위 집합이 응답에 대한 중복 정보를 포함할 수 있는지 확인합니다.

선형 회귀 모델은 종종 최소 제급 접근법을 사용합니다, 그러나 그들은 또한 그러한 다른 규범(로 그것들은 절대 편차 regression)의"꼭 맞는 부족"을 최소화하거나 리지 회귀(L2-norm 페널티)과 lasso에는 사각형 틀을 비용 함수의penalized 버전을 최소화하여에 의해 같은 다른 방법으로 설치할 수 있는 적합하다.L1(표준 패널티).반대로 최소 제곱법은 선형 모형이 아닌 모형을 적합시키는 데 사용할 수 있습니다.따라서 "최소 제곱"과 "선형 모형"이라는 용어는 밀접하게 연결되어 있지만 동의어는 아닙니다.

공식화

n개의 통계 단위의 데이터 집합${\displaystyle }${${\displaystyle y_{}}$ i${\displaystyle {}_{}}$ ${\displaystyle {\mathrm{x}}_{}}$i 1, ${\displaystyle \dots ,{}_{}}$ ${\displaystyle i_{}}$ ${\displaystyle p_{}}$ ${\displaystyle {}_{}{}_{}^{}}$ ${\displaystyle i_{}^{}}$ $=$ ${\displaystyle {}_{}^{}}$ n {$displaystyle$\{$y_{i},x_{i1}_{n}$일 때 선형 회귀 모형은 종속 변수 y와 x 회귀 변수의 p-recessor 사이의 관계를 가정합니다.이 관계는 의존 변수와 회귀 변수 사이의 선형 관계에 "노이즈"를 추가하는 관측되지 않은 랜덤 변수인 교란 항 또는 오차 변수 θ를 통해 모델링됩니다.따라서 모델은 다음과 같은 형태를 취한다.

$\displaystyle y_{i}=\cdots_{1}+\cdots_{p}x_{ip}+\varepsilon_{i}=\mathbf {x}_{i}{\mathsf {T}}{\boldsymbol {\}+vallepsilon}, _adqilon_{i},$

여기서 xβ는_i^T 전치이므로 xβ는 벡터 x와_i β 사이의 내부 곱이다.

종종 이 n개의 방정식은 함께 쌓이고 행렬 표기로 다음과 같이 쓰여집니다.

${\displaystyle \mathbf {y} = X{\boldsymbol {\boldsymbol {\varepsilon}},}$

어디에

$\displaystyle \mathbf {y} = pmatrix {1}\y_{2}\vdots \\y_{n}\end{pmatrix},\displays }$

${\displaystyle X=begin{pmatrix}\mathbf {x}_{1}^{\mathbf {T}_{2}^{\mathbf {T}\vdots \{n}^{\mathbf {T}\end{pmatrix}=pmatrix1matrix}$

${\displaystyle {\boldsymbol {\pmatrix}=pmatrix_{0}\\vdots_{1}\p}\end{pmatrix}\boldsymbol {varepsilon}=pmatrix_v\v\vdotsypmbol {\}\pmbrapsypmblon_{{\pmb}\p}\pmbrap}\p}\v}\v}\v}\clon_{{{{\p}\p}}$

표기법 및 용어

• ${\displaystyle \mathbf{y}}${\$displaystyle \mathbf${$y$$} }$는 회귀 변수, 내생 변수, 반응 변수, 측정된 변수, 기준 변수 또는 종속 변수라고 하는 ${\displaystyle {변수}_{}}$의 관측 값$y$ ${\displaystyle i({}_{}\mathrm{i}}$ ${\displaystyle =}$ 1, ${\displaystyle \dots ,}$ $)\$displaystyle $y_${i$}\(i=1,\ldots,$ n$)$의 벡터입니다.이 변수는 예측 변수라고도 하지만 y$^\$로$$표시되는 예측 값과 혼동해서는 안 됩니다.데이터 집합에서 어떤 변수를 종속 변수로 모델링하고 어떤 변수를 독립 변수로 모델링하는지에 대한 결정은 변수 중 하나의 값이 다른 변수에 의해 발생하거나 다른 변수에 의해 직접 영향을 받는다는 가정에 기초할 수 있습니다.대안으로, 한 변수를 다른 변수와 관련하여 모형화해야 하는 운영상의 이유가 있을 수 있으며, 이 경우 인과관계를 추정할 필요가 없다.
• $(\displaystyle$ X$)$는 행 $벡터{\displaystyle {\mathbf{}}_{}}$ $(\$${i})$ 또는 n차원 열 $벡터{\displaystyle {}_{}}$ ${\displaystyle X_{}}$ j$(\$의 매트릭스로 볼 수 있으며, 이들은 회귀 변수, 외인 변수, 공변수, 입력 변수, 예측 변수 또는 독립 변수(예측 변수)로 알려져 있다.독립 랜덤 변수의 개념과 혼동된다).$매트릭스 X$는 디자인 매트릭스라고도$$합니다$$.
  • 일반적으로 상수는 회귀 분석기 중 하나로 포함됩니다.$특히{\displaystyle {\mathbf{}}_{}}$, ${\displaystyle \mathrm{i}}$ ${\displaystyle =}$1, $…,$ ${\displaystyle n}$ {\$displaystyle i=1,\ldots,$n$\}$에 ${\displaystyle {}_{}}$ ${\displaystyle {\mathrm{x}}_{}}$ $=$ 1 {$displaystyle \mathbf {x}$_{i0$}=1$}이다. β에 대응하는 원소를 절편이라고 한다.선형 모델에 대한 많은 통계적 추론 절차는 절편이 존재해야 하므로, 이론적인 고려 사항에서 값이 0이어야 한다고 하더라도 종종 절편이 포함된다.
  • 때로는 다항식 회귀 분석 및 세그먼트 회귀 분석에서처럼 회귀 분석기 중 하나가 다른 회귀 분석기 또는 데이터의 비선형 함수일 수 있습니다.모델은 매개변수 벡터 β에서 선형인 한 선형으로 유지됩니다.
  • 값_ij x는 랜덤 변수_j X의 관측값으로 볼 수도 있고 종속 변수를 관측하기 전에 선택한 고정값으로 볼 수도 있습니다.두 해석 모두 서로 다른 경우에 적절할 수 있으며 일반적으로 동일한 추정 절차로 이어진다. 그러나 점근 분석에 대한 다른 접근법이 이 두 상황에서 사용된다.
• ${\displaystyle }$β$${\$displaystyle$ {\$displaystyle$$}$은$({\displaystyle }$는${\displaystyle )}$ ($p$+ $1)$ 차원 파라미터 벡터입니다.${\displaystyle {여기}_{}}$서 β 0$${$displaystyle \display_{$0$$}은$$(는) 절편어입니다(모델에 포함되는 $경우{\displaystyle \mathit{}}$)$β$ {\displaystyle\displaystyle {\dismbol$}$은 p차원입니다).해당 원소는 효과 또는 회귀 계수(후자 항은 추정된 효과를 위해 예약되는 경우도 있음)로 알려져 있습니다.단순 선형 회귀 분석에서는 p=1이며 계수를 회귀 기울기라고 합니다.선형 회귀에서의 통계적 추정과 추론은 β에 초점을 맞춘다.이 매개 변수 벡터의 요소는 다양한 독립 변수에 대한 종속 변수의 부분 도함수로 해석됩니다.
• ${\$ ( \ display style \ $bold symbol$ \ varepsilon$$} )는 값$$ i ( \$displaystyle$ \ $varepsilon _${ i$$} )의 벡터입니다.모델의 이 부분을 오차항, 교란항 또는 때로는 노이즈라고 합니다(모델의 나머지 부분에서 제공되는 "신호"와는 대조적으로).이 변수는 회귀 변수 x를 제외한 종속 변수 y에 영향을 미치는 다른 모든 요인을 캡처합니다.오차항과 회귀군 사이의 관계(예: 상관 관계)는 적절한 추정 방법을 결정하기 때문에 선형 회귀 모형을 공식화할 때 중요한 고려 사항입니다.

주어진 데이터 세트에 선형 모델을 적합시키려면 일반적으로 오류 ${\displaystyle 조건\mathbf{}}$ ${\displaystyle =}$ ${\displaystyle y\mathit{}}$ -$$X β {\$displaystyle${\$varepsilon$ } $= \mathbf {y}$ -X{\$boldsymbol${\$display}}}$이(가) 최소화되도록 회귀 계수$$β {\$displaystyle}$을 추정해야 합니다.예를 들어 오차의 제곱합 ${\displaystyle {\mathrm{}}_{}^{}}$( $displaystyle$\ bold $symbol$\ $varepsilon$}$_ {2}^2}$)는 최소화를 위해 ${\$ \ $displaystyle$\ bold $symbol$\ $varepsilon }$의 척도로 사용하는 것이 일반적입니다.

예

작은 공이 공중에 던져지는 상황을 고려하여 다양한 시간 t에서_i 상승 높이_i h를 측정합니다.물리학은 우리에게 항력을 무시하면 관계를 다음과 같이 모델링할 수 있다고 말한다.

${{i}=\displaystyle _{1}t_{i}+\display _{2}^{i}+\varepsilon _{i}$

여기서₁ β는 공의 초기 속도를 결정하고₂, β는 표준 중력에 비례하며, β는_i 측정 오류에 의한 것이다.선형 회귀를 사용하여 측정된 데이터에서 β₂ 및 β₁ 값을 추정할 수 있습니다.이 모델은 시간 변수에서는 비선형이지만 매개변수₁ β와₂ β에서는 선형이다. 회귀 분석기_i x = (x_i1, x_i2) = (t_i, t_i²)를 취하면 모델은 표준 형태를 취한다.

${\displaystyle h_{i}=\mathbf {x}_{i}^{\mathsf {T}}{\boldsymbol {\mathsf }}+\varepsilon _{i}.}$

전제 조건

표준 추정 기법을 사용하는 표준 선형 회귀 모형은 예측 변수, 반응 변수 및 이들의 관계에 대해 여러 가지 가정을 합니다.이러한 각 가정을 완화(즉, 더 약한 형태로 축소)할 수 있도록 하는 수많은 확장이 개발되었으며, 경우에 따라서는 완전히 제거되었다.일반적으로 이러한 확장은 추정 절차를 더 복잡하고 시간이 많이 소요되며, 동일한 정밀도 모형을 생성하기 위해 더 많은 데이터가 필요할 수 있습니다.

다음은 표준 추정 기법을 사용한 표준 선형 회귀 모형의 주요 가정이다(예: 일반 최소 제곱).

• 약한 이질성.이는 기본적으로 예측 변수 x가 랜덤 변수가 아닌 고정 값으로 처리될 수 있음을 의미합니다.이는 예를 들어 예측 변수가 오류가 없는 것으로 가정한다. 즉, 측정 오류로 오염되지 않은 것으로 가정한다.이러한 가정은 많은 설정에서 현실적이지 않지만, 이를 삭제하면 변수 내 오차 모형이 훨씬 더 어려워집니다.
• 직선성즉, 반응 변수의 평균이 모수(회귀 계수)와 예측 변수의 선형 조합임을 의미합니다.이 가정은 처음에 보이는 것보다 훨씬 덜 제한적이라는 점에 유의하십시오.예측 변수는 고정 값으로 처리되기 때문에(위 참조), 선형성은 모수에 대한 제한에 불과합니다.예측 변수 자체는 임의로 변환할 수 있으며, 실제로 동일한 기본 예측 변수의 여러 복사본을 각각 다르게 추가할 수 있습니다.예를 들어, 이 기법은 선형 회귀 분석을 사용하여 반응 변수를 예측 변수의 임의의 다항식 함수(최대 일정 정도)로 적합시키는 다항식 회귀 분석에서 사용됩니다.이렇게 유연성이 높기 때문에 다항식 회귀 분석과 같은 모형은 데이터를 과도하게 적합시키는 경향이 있기 때문에 "너무 많은 검정력"을 갖는 경우가 많습니다.따라서 견적 프로세스에서 불합리한 해결책이 나오지 않도록 하기 위해 일반적으로 일정한 정규화를 사용해야 합니다.일반적인 예로는 능선 회귀 분석과 Lasso 회귀 분석을 들 수 있습니다.베이지안 선형 회귀도 사용할 수 있는데, 이는 본질적으로 과적합 문제에 대해 다소 면역성이 있다.(실제로 능선 회귀와 라소 회귀는 모두 회귀 계수에 배치된 특정 유형의 이전 분포와 함께 베이지안 선형 회귀의 특수한 경우로 볼 수 있습니다.)
• 상수 분산(일명 동질성)입니다.즉, 오차의 분산이 예측 변수 값에 따라 달라지지 않습니다.따라서 예측 변수의 주어진 고정 값에 대한 반응의 변동성은 반응의 크기 또는 크기에 관계없이 동일합니다.일반적으로 평균이 큰 변수는 평균이 작은 변수보다 분산이 크기 때문에 그렇지 않은 경우가 많습니다.예를 들어 소득이 100,000달러인 사람은 실제 소득이 80,000달러 또는 120,000달러(즉, 표준 편차는 약 20,000달러)인 반면, 10,000달러의 예상 소득을 가진 다른 사람은 20,000달러의 표준 편차를 가질 가능성이 낮다. 이는 실제 소득이 어디에서나 달라질 수 있기 때문이다.$10,000 및 $30,000. (실제로, 많은 경우에서 알 수 있듯이, 정규 분포 오류의 가정이 실패하는 경우와 같은 경우) 분산 또는 표준 편차는 일정하지 않고 평균에 비례하는 것으로 예측해야 한다.)균질성이 없는 것을 이질성이라고 한다.이 가정을 확인하기 위해 잔차 대 예측 값(또는 각 개별 예측 변수의 값)의 그래프에서 "패닝 효과"(즉, 그림에서 왼쪽에서 오른쪽으로 이동할 때 수직 범위 증가 또는 감소)를 조사할 수 있습니다.절대 잔차 또는 제곱 잔차 대 예측 값(또는 각 예측 변수)의 그림에서도 추세 또는 곡면성을 조사할 수 있습니다.정식 테스트도 사용할 수 있습니다. 이질적 탄성을 참조하십시오.헤테로세사스틱성이 존재하면 실제 분산 구조를 고려하는 추정치 대신 전체적인 "평균" 분산 추정치가 사용됩니다.따라서 정확도가 낮아지고(그러나 일반적인 최소 제곱의 경우, 편향되지 않음) 모수 추정치와 편향된 표준 오차가 발생하여 잘못된 검정과 구간 추정치가 발생합니다.모형의 평균 제곱 오차도 틀립니다.가중 최소 제곱 및 헤테로세사성 일관성 표준 오차 사용을 포함한 다양한 추정 기법은 매우 일반적인 방법으로 헤테로세사성을 처리할 수 있다.베이지안 선형 회귀 기법은 분산이 평균의 함수라고 가정할 때도 사용할 수 있다.반응 변수에 변환을 적용하여 문제를 해결할 수도 있습니다(예: 선형 회귀 모형을 사용하여 반응 변수의 대수를 적합시키는 것, 즉 반응 변수 자체에 정규 분포가 아닌 로그 정규 분포가 있음을 의미함).

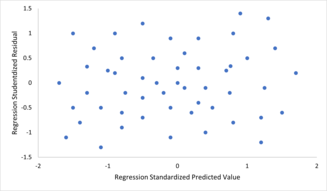
• 오류의 독립성.이는 반응 변수의 오차가 서로 상관관계가 없다고 가정한다(실제 통계적 독립성은 단순히 상관관계가 없는 것보다 더 강력한 조건이며 종종 필요하지 않지만, 유지되는 것으로 알려진 경우에는 악용될 수 있다).일반화 최소 제곱과 같은 일부 방법은 상관 오류를 처리할 수 있지만, 일반적으로 상관되지 않은 오류를 가정하는 데 일정한 정규화를 사용하지 않는 한 훨씬 더 많은 데이터를 필요로 합니다.베이지안 선형 회귀는 이 문제를 처리하는 일반적인 방법입니다.
• 예측 변수의 완벽한 다중 공선성이 결여되어 있습니다.표준 최소 제곱 추정 방법의 경우 설계 행렬 X의 열 순위가 p여야 합니다. 그렇지 않으면 예측 변수에 완전한 다중 공선성이 존재하므로 둘 이상의 예측 변수 사이에 선형 관계가 존재합니다.이는 데이터의 변수를 실수로 복제하거나, 변수의 선형 변환(예: 화씨 및 섭씨로 표시되는 동일한 온도 측정값)을 사용하거나, 평균과 같은 여러 변수의 선형 조합을 모델에 포함시킴으로써 발생할 수 있습니다.모수 수에 비해 사용 가능한 데이터가 너무 적어서 추정할 수 없는 경우에도 발생할 수 있습니다(예: 회귀 계수보다 데이터 점이 적음).예측 변수가 매우 높지만 완벽하게 상관되지 않는 경우 이 가정을 거의 위반하면 모수 추정치의 정밀도를 떨어뜨릴 수 있습니다(분산 인플레이션 요인 참조).완벽한 다중 공선성의 경우, 매개변수 벡터 β는 식별 불가능할 것이다. 즉, 고유한 솔루션이 없다.이 경우 파라미터의 일부만을 식별할 수 있다(즉, 그 값은 풀 파라미터 공간^p R의 일부 선형 부분공간 내에서만 추정할 수 있다).자세한 내용은 부분 최소 제곱법을 참조하십시오.다중 공선성을 가진 선형 모델을 적합시키는 방법이 ^[5][6][7][8]개발되었으며, 그 중 일부는 효과의 큰 부분이 정확히 0이라는 "효과 희소성"과 같은 추가적인 가정을 필요로 한다.범용 선형 모델에서 사용되는 알고리즘과 같이 파라미터 추정을 위해 계산 비용이 더 많이 드는 반복 알고리즘은 이 문제를 겪지 않습니다.

이러한 가정을 넘어, 데이터의 몇 가지 다른 통계적 특성은 서로 다른 추정 방법의 성능에 강하게 영향을 미친다.

• 오차항과 회귀군 사이의 통계적 관계는 추정 절차가 편향되지 않고 일관되는 것과 같은 바람직한 표본 추출 특성을 가지고 있는지 여부를 결정하는 데 중요한 역할을 합니다.
• 예측 변수 x의 배열 또는 확률 분포는 β 추정의 정밀도에 큰 영향을 미친다. 표본 추출과 실험 설계는 β의 정확한 추정치를 달성하기 위한 방법으로 데이터를 수집하기 위한 지침을 제공하는 고도로 개발된 통계 하위 분야이다.

해석

적합 선형 회귀 모형을 사용하여 모형의 다른 모든 예측 변수가 "고정 상태"인 경우 단일 예측 변수_j x와 반응 변수 y 사이의 관계를 식별할 수 있습니다.구체적으로, β의_j 해석은 다른 공변량이 고정된 경우 x의 단일_j 단위 변화에 대한 y의 예상 변화이다. 즉, x에 대한_j y의 부분 도함수의 예상 값이다.이것은 때때로 y에 대한 x의 고유한_j 효과라고 불립니다.반대로, y에 대한 x의 한계_j 효과는 x와 y에만 관련된_j 상관 계수 또는 단순 선형 회귀 모델을 사용하여 평가할 수 있습니다. 이 효과는 x에 대한_j y의 총 도함수입니다.

회귀 결과를 해석할 때 주의해야 한다. 일부 회귀 분석기는 한계 변화를 허용하지 않는 반면(예: 더미 변수 또는 절편 항) 다른 회귀 분석기는 고정 상태를 유지할 수 없기 때문이다(서론에서 예제를 호출하면 "고정 상태 유지_i"가 불가능하고 동시에 t의 값을 변경할_i² 수 있다).

한계 효과가 큰 경우에도 고유 효과가 거의 0일 수 있습니다.이는 다른 공변량이 x의 모든_j 정보를 캡처하므로 해당 변수가 모형에 포함되면 y의 변동에 x의_j 기여가 없다는 것을 의미할 수 있습니다.반대로 x의 고유한_j 효과는 클 수 있지만 한계 효과는 거의 0입니다.다른 공변량이 y의 변동을 많이 설명하는 경우 이러한 현상이 발생하지만, 주로 x가 포착하는_j 변동을 보완하는 방식으로 설명합니다.이 경우 모형에 다른 변수를 포함하면 x와 관련이_j 없는 y의 변동성이 감소하여 x와의 관계가_j 강화됩니다.

"고정 고정" 식의 의미는 예측 변수 값이 발생하는 방식에 따라 달라질 수 있습니다.실험자가 연구 설계에 따라 예측 변수의 값을 직접 설정하는 경우 관심 있는 비교는 말 그대로 예측 변수가 "고정"된 단위 간의 비교에 해당할 수 있습니다.또는 "고정 보유"라는 표현은 데이터 분석의 맥락에서 이루어지는 선택을 나타낼 수 있습니다.이 경우 주어진 예측 변수에 대해 공통 값을 갖는 데이터의 하위 집합으로 주의를 제한하여 "변수를 고정"합니다.이는 관측 연구에서 사용할 수 있는 "고정 고정"에 대한 유일한 해석입니다.

"독특한 효과"의 개념은 여러 개의 상호 연관된 성분이 반응 변수에 영향을 미치는 복잡한 시스템을 연구할 때 매력적입니다.일부 경우에는 말 그대로 예측 변수 값과 연관된 개입의 인과 효과로 해석될 수 있습니다.그러나 예측 변수들이 서로 상관되어 있고 연구 ^[9]설계에 따라 할당되지 않은 경우, 많은 경우 다중 회귀 분석이 예측 변수와 반응 변수 사이의 관계를 명확히 하지 못한다는 주장이 제기되었다.

내선번호

선형 회귀의 수많은 확장이 개발되었으며, 이를 통해 기본 모델의 기초가 되는 가정의 일부 또는 모두를 완화시킬 수 있다.

단순 및 다중 선형 회귀 분석

단일 스칼라 예측 변수 x와 단일 스칼라 반응 변수 y의 가장 단순한 경우를 단순 선형 회귀 분석이라고 합니다.다중 및/또는 벡터 값 예측 변수에 대한 확장(대문자 X로 표시)을 다중 선형 회귀 분석이라고 하며 다변량 선형 회귀 분석이라고도 합니다(다변량 선형 회귀^[10] 분석과 혼동하지 마십시오).

다중 선형 회귀는 둘 이상의 독립 변수의 경우 단순 선형 회귀를 일반화하며, 종속 변수가 하나만 있는 일반 선형 모형의 특수한 경우입니다.다중 선형 회귀 분석의 기본 모형은 다음과 같습니다.

$\displaystyle Y_{i}=\beta _{0}+\beta _{i1}+\beta _{2}X_{i2}+\ldots +\beta _{p}X_{ip}+\epsilon _{i}$

각 관측치에 대해 i = 1, ..., n.

위의 공식에서는 하나의 종속 변수와 p 독립 변수에 대한 n개의 관측치를 고려합니다.따라서_ij, Y는 종속 변수의^th i 관측치이고_ij, X는^th j 독립 변수의^th i 관측치이고, j = 1, 2, ..., p. 값 β는 추정해야 할 모수를 나타내며, β는_i i 독립^th 동일 분포 정규 오차이다.

보다 일반적인 다변량 선형 회귀 분석에서는 동일한 설명 변수 집합을 공유하여 서로 동시에 추정하는 m > 1 종속 변수 각각에 대해 위의 형식의 방정식이 하나 있습니다.

$\displaystyle Y_{ij}=\beta_{0j}+\beta_{i1}+\beta_{2j}X_{i2}+\ldots+{pj}X_{ip}+\epsilon_{ij}$

i = 1, ... , n으로 지수화된 모든 관측치와 j = 1, ... , m으로 지수화된 모든 종속 변수에 대해.

거의 모든 실제 회귀 모형에는 여러 예측 변수가 포함되며 선형 회귀에 대한 기본적인 설명은 종종 다중 회귀 모형으로 표현됩니다.단, 이 경우 응답 변수 y는 여전히 스칼라입니다.다변량 선형 회귀 분석이라는 또 다른 용어는 y가 벡터인 경우, 즉 일반 선형 회귀 분석과 동일한 경우를 가리킵니다.

일반 선형 모델

때 응답 변수가 아니다 스칼라(각 관찰을 위한) 하지만 벡터, 의:일반 선형 모델은 상황을 고려하고 있다.E(y∣)나는)))나는 TB(_{나는}^{\mathsf{T}}B}는 여전히 매트릭스 B벡터 β한 것으로 추정된다 o.의 조건부 직선성f 고전적 선형 회귀 모형.일반 최소 제곱(OLS)과 일반화 최소 제곱(GLS)의 다변량 유사점이 개발되었다."일반 선형 모형"은 "다변량 선형 모형"이라고도 합니다.이러한 모형은 다변수 선형 모형("복수 선형 모형"이라고도 함)과 다릅니다.

이질구조 모형

이질성을 허용하는 다양한 모델이 생성되었다. 즉, 다른 반응 변수에 대한 오차는 서로 다른 분산을 가질 수 있다.예를 들어, 가중 최소 제곱은 반응 변수의 오차 분산이 서로 다를 수 있는 경우 선형 회귀 모형을 추정하는 방법입니다(가중 선형 최소 제곱 및 일반화 최소 제곱 참조).헤테로세사스틱 일관성 표준 오류는 상관관계가 없지만 잠재적으로 헤테로세사스틱 오류와 함께 사용하기 위한 개선된 방법입니다.

일반화 선형 모델

일반화 선형 모형(GLM)은 경계 또는 이산 반응 변수를 모형화하기 위한 프레임워크입니다.이것은 다음과 같이 사용됩니다.

• 대규모에 걸쳐 변화하는 양의 양(예: 가격 또는 모집단)을 모델링할 때, 로그 정규 분포 또는 포아송 분포와 같이 왜곡된 분포를 사용하여 더 잘 설명된다(GLM은 로그 정규 데이터에 사용되지 않지만 대신 반응 변수는 단순히 로그 함수를 사용하여 변환된다).
• 유의하게 순서가 매겨질 수 없는 선택의 수가 고정된 선거에서의 후보 선택(이항 선택의 경우 베르누이 분포/이항 분포를 사용하여 더 잘 설명됨)과 같은 범주형 데이터를 모델링할 때
• 순서형 데이터를 모델링할 때(예: 0부터 5까지의 척도의 등급), 서로 다른 결과를 정렬할 수 있지만 수량 자체는 절대적인 의미가 없을 수 있다(예: 4등급은 2등급만큼 객관적인 의미에서 "좋지 않을 수 있다"는 것이 아니라 단순히 2등급이나 3등급보다는 낫지만 5등급만큼 좋지는 않다는 것을 나타낸다).

일반화 선형 모델에서는 반응 변수의 평균을 예측 변수에 관련짓는 임의의 링크 함수 g를 허용합니다. $E{\displaystyle }$(${\displaystyle Y}$ ) ${\displaystyle ={}^{}}$ -${\displaystyle {}^{}{1}^{}}$ ( ${\displaystyle X}$ B$$) \ $displaystyle$E ( Y ) =$g^$ { -$1$ ( $XB$)$$}링크 함수는 응답의 분포와 관련된 경우가 많으며, 특히 선형 프레딕터의${\displaystyle }$(${\displaystyle }$-${\displaystyle }$" ,${\displaystyle }$"${\displaystyle \mathrm{}}$)$$\ $displaystyle$ ( - \ $infty$, \ $infty )$ 범위와$$ 응답 변수의 범위 사이에서 변환되는 효과가 있습니다.

GLM의 일반적인 예는 다음과 같습니다.

• 카운트 데이터에 대한 포아송 회귀 분석.
• 이항 데이터에 대한 로지스틱 회귀 분석 및 프로빗 회귀 분석.
• 범주형 데이터에 대한 다항 로지스틱 회귀 분석 및 다항 프로빗 회귀 분석입니다.
• 순서형 데이터에 대한 순서형 로짓 및 순서형 프로빗 회귀 분석.

단일 지수^{[clarification needed]} 모델은 x와 y 사이의 관계에서 어느 정도 비선형성을 허용하며, 기존의 선형 회귀 모델에서와 같이 선형 예측 변수 βδx의 중심 역할을 보존한다.특정 조건에서는 단일 지수 모델의 데이터에 OLS를 적용하는 것만으로 β를 비례 ^[11]상수까지 일관되게 추정할 수 있다.

계층적 선형 모형

계층적 선형 모형(또는 다단계 회귀 분석)은 데이터를 회귀 계층(예: A가 B에서 회귀되고 B가 C에서 회귀)으로 구성합니다.관심 변수가 교실에 중첩되고, 교실이 학교에 중첩되며, 학교가 학군과 같은 일부 행정 그룹에 중첩되는 교육 통계와 같이 자연스러운 계층 구조를 가질 때 자주 사용됩니다.반응 변수는 검정 점수와 같은 학생의 성취도에 대한 측정값일 수 있으며 교실, 학교 및 학군 수준에서 서로 다른 공변량이 수집됩니다.

변수 오류

변수 내 오차 모형(또는 "측정 오차 모형")은 전통적인 선형 회귀 모형을 확장하여 예측 변수 X를 오차로 관측할 수 있도록 합니다.이 오류로 인해 β의 표준 추정치가 편향됩니다.일반적으로 바이어스의 형태는 감쇠이며, 이는 효과가 0으로 치우쳐 있음을 의미합니다.

다른이들

• 뎀프스터-셰퍼 이론 또는 특히 선형 신념 함수에서 선형 회귀 모델은 부분적으로 스위프된 행렬로 표현될 수 있으며, 이는 관측치를 나타내는 유사한 행렬과 다른 가정된 정규 분포 및 상태 방정식과 결합될 수 있다.스윕 또는 비위축 행렬의 조합은 선형 회귀 모형을 추정하기 위한 대체 방법을 제공합니다.

견적방법

선형 회귀 분석에서 모수 추정 및 추론을 위해 많은 절차가 개발되었습니다.이러한 방법은 알고리즘의 계산 단순성, 폐쇄형 솔루션의 존재, 두꺼운 꼬리 분포에 대한 견고성 및 일관성 및 점근 효율과 같은 바람직한 통계 특성을 검증하는 데 필요한 이론적 가정 등에서 다르다.

선형 회귀 분석의 일반적인 추정 기법 중 일부는 아래에 요약되어 있습니다.

최소 제곱 추정 및 관련 기술

독립 변수가 $x{\displaystyle \stackrel{}{{}_{}}}$ ${\displaystyle \stackrel{}{i_{}}}$ ${\displaystyle \to }$ [ ${\displaystyle {x\mathrm{}}_{}^{}}$ 1${\displaystyle {}_{}^{}}$ , ${\displaystyle {x\mathrm{}}_{}^{}}$ ${\displaystyle {}_{}^{}}$i , ${\displaystyle ...}$ , ${\displaystyle {}_{}^{}}$ ${\displaystyle m_{}^{}{}_{}^{}}$ $]$ {$display$ { $vec${ $x$_ { i } = \$left$ [ ${\displaystyle x{}_{}}$$_$ { 1 }^{$i$ , x$_$ { $2$}^{ i , \$ldots$, x$_$ m }^{$i$} \ right$$}라고 가정하면, ${\displaystyle {}_{}}$의 $파라미터$는 β${\displaystyle {}_{}\to }$ 1${\displaystyle {}_{}}$,${\displaystyle }$, , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , .$\ldots ,\dots _${m$}\right$ 그러면 모델의 예측은 다음과 같습니다.

${\displaystyle {}_{}\underset{}{\overset{}{\mathrm{y}}}}$ ${\displaystyle {}_{}}$ $β$ ${\displaystyle {0\mathrm{}}_{}}$ + ${\displaystyle \underset{}{\overset{}{}}}$ ${\displaystyle \underset{}{\overset{}{j}}}$ ${\displaystyle \underset{}{\overset{}{=}}}$ ${\displaystyle 1_{}}$ m${\displaystyle {}_{}{}_{}^{}}$ j × ${\displaystyle x_{}^{}}$ $i$ { $displaystyle$y _ { i } \$about$_ { 0 } + \$sum$ _ { j$$=$$1$}^{$m } \$times$x _ { j }^{$i$$$。

${\displaystyle \stackrel{}{x_{}}}$ i $→$ {\$displaystyle {x_{i}}}$이(가) ${\displaystyle \stackrel{}{x_{}}}$ i $=$ [${\displaystyle {}_{}^{}}$,${\displaystyle {x\mathrm{}}_{}^{}}$ ${\displaystyle {}_{}^{}}$i, ${\displaystyle {}_{}^{}}$ ${\displaystyle {}_{}^{}}$i${\displaystyle ,}$ ${\displaystyle ...,}$ ${\displaystyle {}_{}^{}}$ ${\displaystyle {}_{}^{}}$i$](\$})=\$left[1,x_{1}^{i},\ldots,x_{m$^{i}${\displaystyle i_{}}$$})$ $i$로 확장되면 $y{\displaystyle \stackrel{}{{}_{}}}$$,$ $오른쪽{\displaystyle {}_{}}$$,$할 수 있다, 즉,

${\displaystyle y_{}}$ ${\displaystyle {}_{}}$ i ${\displaystyle \underset{}{\overset{}{}}}$ ${\displaystyle \underset{}{\overset{}{j}}}$ ${\displaystyle \underset{}{\overset{}{=}}}$ ${\displaystyle 0\stackrel{}{}}$ ${\displaystyle \underset{}{\overset{}{}}{}_{}}$ ${\displaystyle {\beta }_{}}$j × ${\displaystyle {}_{}^{}}$ ${\displaystyle j_{}^{}}$ i ${\displaystyle {}_{}^{}}$ ${\displaystyle \beta \stackrel{}{{}_{}}}$ ${\displaystyle \stackrel{}{\to }}$ ${\displaystyle \cdot }$ ${\displaystyle \stackrel{}{x_{}}}$ x i $→$ { $display$ style y$_$ { $i$} \$about$ \$sum$_$${$$j$$= 0 }^{ $m$} \ $sum$_ { $j$} \ times $x$_ { $j$}^{ i$$=$cdevec${ x _ x _ x _ { $i}$ } } } }$$} }} y { $cdot${$cdevec${ i} } y y 。

최소 제곱 설정에서 최적 매개변수는 평균 제곱 손실의 합을 최소화하도록 정의됩니다.

$(\displaystyle {\vec } = 언더셋 {\mbox {\mbox} } = 언더셋 {\vec } {\mbox {{n} } } = 언더셋 {\mbox {\cdve} } } = 언더셋 {i= 1 ^{n} {\cdvec } } } left cdvec }$

이제 행렬$X{\displaystyle }$(\$displaystyle$ X$)$와 Y$(\displaystyle$ Y$)$에 각각 독립 변수와 종속 변수를 넣으면 손실 함수를 다음과 같이 다시 작성할 수 있습니다.

$디스플레이 스타일L\left(D, {\vec {\vec }\오른쪽)&=X{-Y}\left(X{\vec {\vec}-Y\오른쪽)^{\textsf {T}}\left(X{\vec }-Y}\오른쪽)\&=Y^{\textsf {T}Y-Y^{\textsf {T}}X{\vec {T}}-{\vec {T}}X^{\textsf {T}}Y+{\vec }}{\textsf {T}}X}X{\textsf }$

손실이 볼록하므로 최적 해법은 구배 0에 있습니다.손실 함수의 구배는 다음과 같습니다(분모 배치 규칙을 사용).

${\displaystyle{\begin{정렬}{\frac{\partial L\left(D,{\vec{\beta}}\right)}{\partial{{\beta\vec}}}}&={\frac{\partial \left(Y^{\textsf{T}}Y-Y^{\textsf{T}}X{\vec{\beta}}-{\vec{\beta}}^{\textsf{T}}X^{\textsf{T}}Y+{\vec{\beta}}^{\textsf{T}}X^{\textsf{T}}X{\vec{\beta}}\right)}{\partial{{\beta\vec}}}}\\&, =-2X^{\textsf{T}.}Y+2X^{)textsf {T}}X{\vec {beta }}\end {aligned}}$

구배를 0으로 설정하면 최적의 파라미터가 생성됩니다.

${\displaystyle {begin{aligned}-2X^{\textsf {T}}Y+2X^{\textsf {T}}X{\vec {\vec}}&=0\\rightarrow X^{\textsf {T}}}Y&=X^{\textsf {T}X{\vec {\hat}}\오른쪽 화살표(X^{\textsf {T}X\right)^{\textsf {T}}X^{\end aligned})$

주의: 얻어진${\displaystyle \stackrel{}{}}$β$^(\$hat$\beta$})가 실제 최소값임을 증명하려면 헤시안 매트릭스를 얻기 위해 다시 한 번 미분하여 양의 확정임을 보여야 합니다.이것은 가우스-마르코프 정리에 의해 제공된다.

선형 최소 제곱 방법에는 주로 다음이 포함됩니다.

• 정규 최소 제곱
• 가중 최소 제곱
• 일반화 최소 제곱

최대우도 추정 및 관련 기술

• 오차항의 분포가 확률 ^[13]분포의 특정 모수족 θ에_θ 속하는 것으로 알려진 경우 최대우도 추정을 수행할 수 있습니다.f가 평균과 분산이 0인 정규 분포일 경우_θ 결과 추정치는 OLS 추정치와 동일합니다.GLS 추정치는 θ가 알려진 공분산 행렬이 있는 다변량 정규 분포를 따를 때 최대우도 추정치입니다.
• 능선 회귀^[14][15][16] 및 기타 형태의 불이익 추정(예: 라소 회귀)^[5]은 추정의 가변성을 줄이기 위해 의도적으로 β의 추정에 편견을 도입한다.결과 추정치는 일반적으로 다중 공선성이 존재하거나 과적합에 문제가 있는 경우 OLS 추정치보다 평균 제곱 오차가 낮습니다.일반적으로 아직 관측되지 않은 예측 변수 x의 값에 대한 반응 변수 y의 값을 예측하는 데 사용됩니다.이러한 방법은 편향을 설명하기 어렵기 때문에 추론이 목표일 때 자주 사용되지 않는다.
• 최소 절대 편차(LAD) 회귀는 특이치의 존재에 대해 OLS보다 덜 민감하다는 점에서 강력한 추정 기법입니다(그러나 특이치가 존재하지 않는 경우 OLS보다 덜 효율적입니다).이는 ^[17]θ에 대한 Laplace 분포 모형에서의 최대우도 추정과 동일합니다.
• 적응형 평가.If we assume that error terms are independent of the regressors, ${\displaystyle \varepsilon _{i}\perp \mathbf {x} _{i}}$, then the optimal estimator is the 2-step MLE, where the first step is used to non-parametrically estimate the distribution of the error term.^[18]

기타 추정 기법

• 베이지안 선형 회귀는 베이지안 통계의 프레임워크를 선형 회귀에 적용합니다.자세한 내용은 베이지안 다변량 선형 회귀 분석을 참조하십시오.특히 회귀계수β는 특정 사전분포를 갖는 랜덤변수로 가정한다.이전 분포에서는 회귀 계수에 대한 솔루션을 능선 회귀 분석 또는 Lasso 회귀 분석과 유사하지만 더 일반적인 방식으로 치우칠 수 있습니다.또한, 베이지안 추정 프로세스는 회귀 계수의 "최상" 값에 대한 단일 점 추정치가 아니라 수량을 둘러싼 불확실성을 완전히 설명하는 전체 사후 분포를 생성한다.이 값은 평균, 모드, 중위수, 모든 분위수(분위수 회귀 참조) 또는 후방 분포의 다른 함수를 사용하여 "최적" 계수를 추정하는 데 사용할 수 있습니다.
• 분위수 회귀 분석에서는 주어진 X의 조건부 평균보다는 주어진 X의 조건부 분위수에 초점을 맞춥니다.선형 분위수 회귀는 예측 변수의 선형 함수 βx로^T 특정 조건부 분위수(예: 조건부 중위수)를 모델링합니다.
• 혼합 모형은 종속성이 알려진 구조를 가진 경우 종속 데이터가 포함된 선형 회귀 관계를 분석하는 데 널리 사용됩니다.혼합 모델의 일반적인 적용에는 세로 데이터 또는 클러스터 샘플링에서 얻은 데이터와 같은 반복 측정과 관련된 데이터 분석이 포함됩니다.이들은 일반적으로 최대우도 또는 베이지안 추정을 사용하여 모수 모형으로 적합됩니다.오차를 정규 랜덤 변수로 모형화하는 경우 혼합 모형과 일반화 최소 ^[19]제곱 사이에는 밀접한 관계가 있습니다.고정 효과 추정은 이러한 유형의 데이터를 분석하는 다른 방법입니다.
• 주성분 회귀 분석(PCR)^[7][8]은 예측 변수의 수가 많거나 예측 변수 사이에 강한 상관 관계가 있을 때 사용됩니다.이 2단계 절차에서는 먼저 주성분 분석을 사용하여 예측 변수를 줄인 다음 축소된 변수를 OLS 회귀 적합에서 사용합니다.실제로는 잘 작동하지만 예측 변수의 가장 유용한 선형 함수가 예측 변수의 다변량 분포의 주요 주성분 사이에 있어야 하는 일반적인 이론적 이유는 없습니다.부분 최소 제곱법은 언급된 결핍을 겪지 않는 PCR 방법의 확장이다.
• 최소 각도 회귀는^[6] 관측치보다 공변량이 많을 수 있는 고차원 공변량 벡터를 처리하기 위해 개발된 선형 회귀 모형에 대한 추정 절차입니다.
• 테일-센 추정기는 표본점 쌍을 통해 적합선의 기울기를 선의 기울기의 중앙값으로 선택하는 단순한 강력한 추정 기법입니다.단순 선형 회귀 분석과 통계 효율성 특성이 유사하지만 ^[20]특이치에 훨씬 덜 민감합니다.
• α-트리밍 평균^{[citation needed]} 접근법과 L-, M-, S- 및 R-추정기를 포함한 다른 강력한 추정 기법이 ^{[citation needed]}도입되었다.

적용들

선형 회귀는 생물, 행동 및 사회과학에서 변수 간의 가능한 관계를 설명하기 위해 널리 사용됩니다.이러한 분야에서 사용되는 가장 중요한 도구 중 하나로 평가됩니다.

트렌드 라인

추세선은 다른 성분이 고려된 이후의 시계열 데이터의 장기 이동인 추세를 나타냅니다.특정 데이터 세트(GDP, 유가 또는 주가)가 기간 동안 증가했는지 감소했는지 여부를 나타냅니다.추세선은 단순히 데이터 점 집합을 통해 눈으로 그릴 수 있지만 선형 회귀 분석과 같은 통계 기법을 사용하여 위치와 기울기를 계산합니다.추세선은 일반적으로 직선이지만, 일부 변동에서는 선에서 원하는 곡면 정도에 따라 더 높은 차수의 다항식을 사용합니다.

트렌드 라인은 비즈니스 분석에서 시간 경과에 따른 데이터 변화를 나타내기 위해 사용되기도 합니다.이것은 간단하다는 장점이 있다.트렌드 라인은 특정 액션이나 이벤트(훈련이나 광고 캠페인 등)가 특정 시점에서 관찰된 변화를 일으켰다고 주장하기 위해 자주 사용됩니다.이는 단순한 기술로 제어 그룹, 실험 설계 또는 정교한 분석 기술이 필요하지 않습니다.그러나 다른 잠재적 변화가 데이터에 영향을 미칠 수 있는 경우에는 과학적 타당성이 결여되어 있습니다.

역학

흡연과 사망률 및 질병률과 관련된 초기 증거는 회귀 분석을 사용한 관찰 연구에서 나왔다.관측 데이터를 분석할 때 유사 상관 관계를 줄이기 위해 연구자들은 일반적으로 일차 관심 변수 외에 여러 변수를 회귀 모형에 포함합니다.예를 들어, 흡연은 일차 관심사의 독립 변수이고 종속 변수는 년 단위로 측정된 수명인 회귀 모델에서, 연구자들은 수명에 대한 흡연의 관찰된 영향이 다른 사회 경제 때문에 발생하지 않도록 하기 위해 교육과 소득을 추가적인 독립 변수로 포함할 수 있다.c 요인그러나 경험적 분석에 가능한 모든 교란 변수를 포함할 수는 없다.예를 들어, 가상의 유전자는 사망률을 증가시키고 또한 사람들이 담배를 더 피우게 할 수 있다.이러한 이유로 랜덤화 대조 시험은 종종 관측 데이터의 회귀 분석을 사용하여 얻을 수 있는 것보다 인과 관계에 대한 더 설득력 있는 증거를 생성할 수 있다.통제된 실험이 가능하지 않은 경우, 기구 변수 회귀 분석과 같은 회귀 분석의 변형을 사용하여 관측 데이터로부터 인과 관계를 추정할 수 있습니다.

자금

자본자산가격결정모델은 선형회귀와 베타 개념을 사용하여 투자의 체계적인 리스크를 분석하고 수량화합니다.이는 투자수익률과 모든 위험자산의 수익률을 관련짓는 선형회귀모형의 베타계수에서 직접 발생한다.

경제학

선형 회귀는 경제학에서 지배적인 경험적 도구이다.예를 들어, 소비 지출,^[21] 고정 투자 지출, 재고 투자, 한 국가의 ^[22]수출 구매, ^[22]수입 지출, 유동 ^[23]자산 보유 수요, 노동 ^[24]수요 및 노동 ^[24]공급을 예측하는 데 사용됩니다.

환경과학

이 섹션은 확장해야 합니다.추가함으로써 도움이 될 수 있습니다. (2010년 1월)

선형 회귀는 광범위한 환경 과학 응용 분야에 적용됩니다.캐나다에서 환경 효과 모니터링 프로그램은 어류 및 해저 조사에 대한 통계 분석을 사용하여 펄프 밀 또는 금속 광산 유출물이 수생 ^[25]생태계에 미치는 영향을 측정합니다.

기계 학습

선형 회귀는 기계 학습으로 알려진 인공지능의 하위 분야에서 중요한 역할을 한다.선형 회귀 알고리즘은 상대적으로 단순하고 잘 알려진 ^[26]특성으로 인해 기본적인 감독 기계 학습 알고리즘 중 하나입니다.

역사

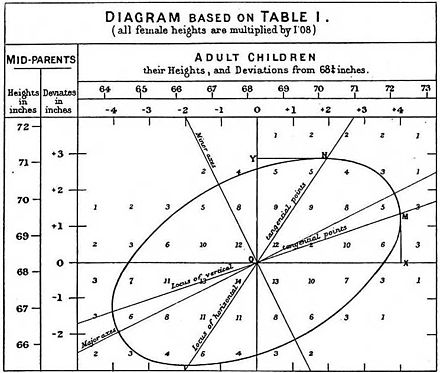
일련의 점에 대한 양호한 대략적인 선형 적합성을 찾기 위한 수단으로 최소 제곱 선형 회귀를 Legendre(1805)와 Gauss(1809)가 행성 이동 예측을 위해 수행했다.Quetete는 이 절차를 널리 알리고 ^[27]사회과학 분야에서 광범위하게 사용하는 데 책임이 있었습니다.

「 」를 참조해 주세요.

레퍼런스

인용문

원천

추가 정보

• Pedhazur, Elazar J (1982). Multiple regression in behavioral research: Explanation and prediction (2nd ed.). New York: Holt, Rinehart and Winston. ISBN 978-0-03-041760-3.
• Mathieu Rouaud, 2013: 확률, 통계 및 추정 제2장: 선형 회귀, 오차 막대를 사용한 선형 회귀 및 비선형 회귀.
• National Physical Laboratory (1961). "Chapter 1: Linear Equations and Matrices: Direct Methods". Modern Computing Methods. Notes on Applied Science. Vol. 16 (2nd ed.). Her Majesty's Stationery Office.

외부 링크

• 최소 제곱 회귀 분석, PhET 대화형 시뮬레이션, 콜로라도 대학교 볼더
• DIY 리니어 핏