베이츠 분포

이 글은 일반적인 참고문헌 목록을 포함하고 있지만, 그에 상응하는 인라인 인용구가 충분하지 않기 때문에 대체로 검증되지 않은 상태로 남아 있다. 좀 더 정밀한 인용구를 도입하여 이 기사를 개선할 수 있도록 도와주십시오. (2011년 6월) (이 템플릿 메시지를 제거하는 방법과 시기 알아보기)

베이츠

확률밀도함수
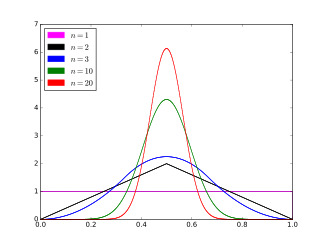누적분포함수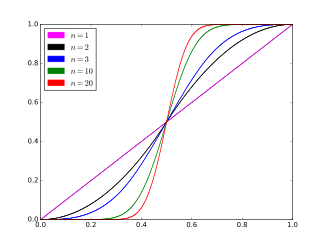
매개변수	$[#################################$ ${\displaystyle n}$ ${\displaystyle \ge }$ ${\displaystyle 1}$ ${\displaystyle n\geq 1}$ 정수$$
지원	$[a,b]에서 [\displaystyle x\in]$
PDF	아래 내용 참조.
평균	${\displaystyle {\tfrac {1}{2}}(a+b)}$
분산	${\displaystyle {\tfrac {1}{12n}(b-a)^{2}}$
왜도	0
엑스트라 쿠르토시스	${\displaystyle -{\tfrac {6}{5n}}$
CF	${\displaystyle \left(-{\frac {in(e^{\tfrac {ibt}{n}-e^{n}-e^{\tfrac {iat}{n}}}}}}{(b-a)t}\오른쪽)^{n}}}$

확률과 통계에서 그레이스 베이츠의 이름을 딴 베이츠 분포는 단위 구간에서 통계적으로 독립된 다수의 균일 분포 랜덤 변수의 평균에 대한 확률 분포다.^[1] 이 분포는 균일, 삼각형 및 정상 가우스 분포와 관련되며, 신호 향상을 위한 방송 엔지니어링에 응용이 있다. 베이츠 분포는 때때로 어윈-홀 분포와 혼동되는데^[2], 이는 0에서 1까지 균일하게 분포된 n개의 독립 랜덤 변수의 합(평균이 아님)의 분포다. 따라서 두 분포는 척도만 다르기 때문에 단순히 서로 다른 버전의 분포일 뿐이다.

정의

Bates 분포는 단위 간격에 대한 독립적이고 균일하게 분포된 랜덤 변수의 평균 X의 연속 확률 분포, U_k:

${\displaystyle X={\frac {1}{n}\sum _{k=1}^{n}U_{k}.}$

Bates 분포 랜덤 변수 X의 확률밀도함수를 정의하는 방정식은

${\displaystyle f_{X}(x;n)={\frac {n}{2(n-1)!}}}\sum _{k=0}^{n(1)^{k}{n \선택 k}(nx-k)^{n-1}\sgnname {sgn}(nx-k)}$

간격(0,1)의 x 및 다른 위치의 0에 대해. 여기서 sgn(nx - k)은 부호 함수를 나타낸다.

${\displaystyle \sgn}(nx-k)={\display{case}-1&nx<0&nx=k\1&nx}k.\end{case}}}$

보다 일반적으로 구간에서 독립적으로 균일하게 분포된 랜덤 변수 n개의 평균 [a,b]

${\displaystyle X_{(a,b)}={\frac {1}{n}}\sum _{k=1}^{n}U_{k}(a,b)}$

확률밀도함수(PDF)를 가질 수 있다.

${\displaystyle g(x;n,a,b)={\frac {1}{b-a}f_{X}\왼쪽({\frac {x-a}{b-a};n\right){\text{}{}a\leq x\leq b}$

확장 및 애플리케이션

이 구간은 확장이 필요하다. 덧셈으로 도움받을 수 있다.(2020년 2월)

몇 가지 수정으로 베이츠 분포는 균일, 삼각형을 포괄하며, n이 무한대로 가는 한계, 또한 가우스 분포의 정상이다.

평균 X를 ${\displaystyle \frac{\sqrt{계산}}{}}$할 때$$ 용어 ${\displaystyle \frac{\mathrm{1n}}{}}${\$displaystyle${\$frac$$${1$}{n1$$}{\sqrt{n$$}}$을(를) 1n ${\$displaystyle {n}{\n$}$로 바꾸면 단결성과 같은 일정한 분산이 있는 유사한 분포가 생성된다$$. 그런 다음 평균을 빼면 분포의 결과 평균이 0으로 설정된다. 따라서 매개변수 n은 순수한 형상 조정 매개변수가 될 것이다. 또한 n을 비정수자로 허용함으로써 U(0,1) + 0.5와 같은 고도로 유연한 분포를 만들 수 있다.U(0,1)는 사다리꼴 분포를 제공한다.

Student-t 분포는 긴 꼬리 데이터의 모델링을 위해 정상적인 가우스 분포의 자연스러운 확장을 제공한다. A 앞서 말한 대로 일반화된 Bates 분포는 짧은 꼬리 데이터에 대해 동일한 목적을 달성한다.

Bates 분포는 전기공학 분야에서 빔포밍과 패턴 합성을 위한 응용 프로그램을 가지고 있다. 분포는 주엽의 빔 폭을 증가시키는 것으로 조사되었는데, 이는 방사선 패턴의 신호의 증가를 한 방향으로 나타내는 동시에, 일반적으로 바람직하지 않은 ^[3]사이드로브 수준을 감소시키는 것으로 나타났다. ^[4]

참고 항목

• 어윈-홀 분포
• 정규 분포
• 중앙 한계 정리
• 균일 분포(연속)
• 삼각분포

참조

추가 읽기

• Bates, G.E. (1955) "일반화된 Polya urn 체계에서 연속적인 사고 발생을 위한 시간 간격의 공동 분포", 수학 통계 연보 26, 705–720