확률분포
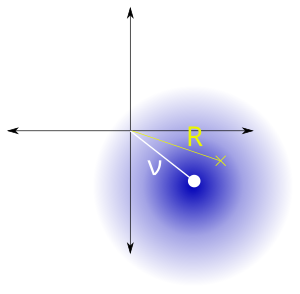
2D 평면에서 원점으로부터 거리 ν 의 고정점을 선택한다. 표준 편차 σ (파란색 영역)를 갖는 가우스 분포와 독립적으로 x 와 y 좌표를 선택하는 지점 중심의 2D 포인트 분포를 생성한다. R 이 이러한 점으로부터 원점까지의 거리인 경우 R 은 쌀 분포를 가진다. 확률밀도함수
누적분포함수
매개변수 ν 0 {\displaystyle \nu \geq }, σ ≥ 0 {\displaystyle \sigma \geq }, 지원 x ∈ [ 0 , ∞ ) [0,\displaystyle x\in [0,\fty )} PDF x σ 2 생략하다 ( − ( x 2 + ν 2 ) 2 σ 2 ) I 0 ( x ν σ 2 ) {\displaystyle {\frac {x}{\frac ^{2}}\exp \left({\frac {-(x^{2}+\nu ^{2}}}}{2\framma ^{2}}}\오른쪽) I_{0}\왼쪽({\frac {x\nu }{\sigma ^{2}}}\오른쪽)} CDF 1 − Q 1 ( ν σ , x σ ) {\displaystyle 1-Q_{1}\왼쪽({\frac {\nu }{\sigma }},{\frac {x}{\sigma }\오른쪽)}}
여기서 Q 는1 Marcum Q 기능 이다. 평균 σ π / 2 L 1 / 2 ( − ν 2 / 2 σ 2 ) {\displaystyle \sigma {\sqrt {\pi /2}}\,\,L_{1/2}(-\nu ^{2}/2\sigma ^{2})} 분산 2 σ 2 + ν 2 − π σ 2 2 L 1 / 2 2 ( − ν 2 2 σ 2 ) {\displaystyle 2\sigma ^{2}+\nu ^{2}-{\frac {\pi \sigma ^{2}}L_{1/2}^{2}\frac {-\nu ^{2}}:{2\sigma ^{2}}:}\오른쪽)} 왜도 (iii) 엑스트라 쿠르토시스 (iii)
확률론 에서 라이스 분포 또는 라이산 분포 (또는 덜 보편적으로 라이산 분포)는 원근대칭 이변량 정규 랜덤 변수 의 크기에 대한 확률 분포 로, 0이 아닌 평균(비중심 분포)일 수 있다. 그것은 스티븐 O 의 이름을 따서 명명되었다. 쌀 (1907–1986)
특성화 확률밀도함수는
f ( x ∣ ν , σ ) = x σ 2 생략하다 ( − ( x 2 + ν 2 ) 2 σ 2 ) I 0 ( x ν σ 2 ) , {\displaystyle f(x\mid \nu ,\flasma )={\frac {x}{\flasma ^{2}}\exp \leftma\frac {-(x^{2}+\nu ^}}{2}}}{2\ma ^2}}\오른쪽) I_{0}\왼쪽({\frac {x\nu }{\sigma ^{2}}}\오른쪽)} 여기서 I 0 (z )는 순서가 0인 첫 번째 종류의 변형된 베셀 함수다.
In the context of Rician fading , the distribution is often also rewritten using the Shape Parameter K = ν 2 2 σ 2 {\displaystyle K={\frac {\nu ^{2}}{2\sigma ^{2}}}} Scale parameter Ω = ν 2 + 2 σ 2 {\display 스타일 \Oomega =\nu ^{2}+2\sigma ^{2}}: . [1]
쌀 분배의 특징적인 기능 은 다음과 같다.[2] [3]
χ X ( t ∣ ν , σ ) = 생략하다 ( − ν 2 2 σ 2 ) [ Ψ 2 ( 1 ; 1 , 1 2 ; ν 2 2 σ 2 , − 1 2 σ 2 t 2 ) + i 2 σ t Ψ 2 ( 3 2 ; 1 , 3 2 ; ν 2 2 σ 2 , − 1 2 σ 2 t 2 ) ] , {\displaystyle {\begin{aligned}\chi _{X}(t\mid \nu ,\sigma )=\exp \left(-{\frac {\nu ^{2}}{2\sigma ^{2}}}\right)&\left[\Psi _{2}\left(1;1,{\frac {1}{2}};{\frac {\nu ^{2}}{2\sigma ^{2}}},-{\frac {1}{2}}\sigma ^{2}t^{2}\right)\right. \\[8pt]&\왼쪽. {}+i{\sqrt {2}}\sigma t\Psi _{2}\left({\frac {3}{2}};1,{\frac {3}{2}};{\frac {\nu ^{2}}{2\sigma ^{2}}},-{\frac {1}{2}}\sigma ^{2}t^{2}\right)\right],\end{aligned}}} where Ψ 2 ( α ; γ , γ ′ ; x , y ) {\displaystyle \Psi _{2}\left(\alpha ;\gamma ,\gamma ';x,y\right)} Horn's confluent hypergeometric functions with two variables and convergent for all finite values of x {\displaystyle x} y {\displaystyle y} [4] [5]
Ψ 2 ( α ; γ , γ ′ ; x , y ) = ∑ n = 0 ∞ ∑ m = 0 ∞ ( α ) m + n ( γ ) m ( γ ′ ) n x m y n m ! n ! , {\displaystyle \Psi _{2}\left(\alpha ;\gamma ,\gamma ';x,y\right)=\sum _{n=0}^{\infty }\sum _{m=0}^{\infty }{\frac {(\alpha )_{m+n}}{(\gamma )_{m}(\gamma ')_{n}}}{\frac {x^{m}y^{n}}{m!n! }},} 어디에
( x ) n = x ( x + 1 ) ⋯ ( x + n − 1 ) = Γ ( x + n ) Γ ( x ) {\displaystyle (x)_{n}=x(x+1)\cdots(x+n-1) ={\frac {\Gamma(x+n)}{\ 감마(x)}}} 상승 요인 이다.
특성. 순간 처음 몇 순간 은 다음과 같다.
μ 1 ′ = σ π / 2 L 1 / 2 ( − ν 2 / 2 σ 2 ) {\displaystyle \mu_{1}^{'}=\sigma {\sqrt {\pi /2}}\,\,L_{1/2}(-\nu ^{2}/2\sigma ^{2}) μ 2 ′ = 2 σ 2 + ν 2 {\displaystyle \mu _{2}^{'}=2\bma ^{2}+\nu ^{2}\,} μ 3 ′ = 3 σ 3 π / 2 L 3 / 2 ( − ν 2 / 2 σ 2 ) {\displaystyle \mu _{3}^{'}=3\sigma ^{3}{\sqrt {\pi /2}}\,\,L_{3/2}(-\nu ^{2}/2\sigma ^{2}}}})} μ 4 ′ = 8 σ 4 + 8 σ 2 ν 2 + ν 4 {\displaystyle \mu _{4}^{'}=8\bma ^{4}+8\bma ^{2}\nu ^{2}+\nu ^4}\,} μ 5 ′ = 15 σ 5 π / 2 L 5 / 2 ( − ν 2 / 2 σ 2 ) {\displaystyle \mu _{5}^{'}=15\sigma ^{5}{\sqrt {\pi /2}}\,\,L_{5/2}(-\nu ^{2}/2\sigma ^{2}}}})} μ 6 ′ = 48 σ 6 + 72 σ 4 ν 2 + 18 σ 2 ν 4 + ν 6 {\displaystyle \mu_{6}^{6}^}=48\buma^{6}+72\buma^{4}\nu ^{2}+18\bu ^{4}+{6}\,},} 그리고, 일반적으로, 생의 순간은
μ k ′ = σ k 2 k / 2 Γ ( 1 + k / 2 ) L k / 2 ( − ν 2 / 2 σ 2 ) . \displaystyle \mu _{k}^{'}=\sigma ^{k2^{k/2}\,\감마 (1\! +\!k/2)\,L_{k/2}(-\nu ^{2}/2\sigma ^{2}). \,} 여기서 L q x )는 Laguerre 다항식 을 나타낸다.
L q ( x ) = L q ( 0 ) ( x ) = M ( − q , 1 , x ) = 1 F 1 ( − q ; 1 ; x ) {\displaystyle L_{q}(x)= L_{q}^{(0)}^(x)=M(-q,1,x)=\,_{1}F_{1}(-q;1;x)} 여기서 M( a z F 1 a b z {\displaystyle M(a,b,z)=_{1}F_{1}(a;b;z)} 결합초기하 함수 다. k 가 짝수일 때, 원시 순간은 위의 예와 같이 in과 ν 에서 단순한 다항식이 된다.
사례 q = 1/2:
L 1 / 2 ( x ) = 1 F 1 ( − 1 2 ; 1 ; x ) = e x / 2 [ ( 1 − x ) I 0 ( − x 2 ) − x I 1 ( − x 2 ) ] . {\displaystyle {\reasoned} L_{1/2}}(x)&=\,_{1}F_{1}F_{1}\왼쪽(-{\frac {1}{1}{1}:{2}};1;x\오른쪽)\ \&=e^{x/2}\왼쪽[\왼쪽(1-x\오른쪽) I_{0}\왼쪽(-{\frac {x}{2}}\오른쪽)-xI_{1}\왼쪽(-{\frac {x}{2}}\오른쪽)\오른쪽] \end{정렬}}} 두 번째 중심 순간 , 분산은
μ 2 = 2 σ 2 + ν 2 − ( π σ 2 / 2 ) L 1 / 2 2 ( − ν 2 / 2 σ 2 ) . {\displaystyle \mu _{2}=2\sigma ^{2}+\nu ^{2}-(\pi \sigma ^{2}/2)\,L_{1/2}^{2}(-\nu ^{2}/2\sigma ^{2}). } Note that L 1 / 2 2 ( ⋅ ) {\displaystyle L_{1/2}^{2}(\cdot )} L 1 / 2 ( ⋅ ) {\displaystyle L_{1/2}(\cdot )} L 1 / 2 ( 2 ) ( ⋅ ) . {\displaystyle L_{1/2}^{(2)}(\cdot ). }
관련 분포 R R i e ν σ {\ displaystyle R\sim \Mathrm Rice} R X 2 Y 2 {\ displaystyle R={\sqrt {X^{2}+ \ nu ,\sigma rigma )}} Y^{2}}}} X ∼ N ( ν cos θ , σ 2 ) {\displaystyle X\sim N\left(\nu \cos \theta ,\sigma ^{2}\right)} Y ∼ N ( ν sin θ , σ 2 ) {\displaystyle Y\sim N\left(\nu \sin \theta ,\sigma ^{2}\right)} θ {\displaystyle \theta } R R c e ν σ {\ displaystyle R\sim \mathrm Rice} \left(\nu ,\sigma rigm)} 1. poisson 분포 가 있는P {\displaystyle P} ν 2 σ {\displaystyle \lambda ={\nu ^{2}}:{ sigma ^{2}}. } 2. 자유도가 2P + 2인 카이-제곱 분포 를갖는 {\displaystyle } 3. 설정 x {\displaystyle =\sigma {\sqrt {X}. } R 쌀 ν {\displaystyle R\sim \operatorname {Rice}(\nu ,1)} 2 {\ displaystyle R^{2}} 자유 parameter 2 {\ displaystystyle \nu ^{2}} 중심 카이-제곱분포를 가진다 . R 쌀 ν {\displaystyle R\sim \operatorname {Rice} (\nu ,1)} R {\displaystyle R} ν {\displaystyle \nu } 분포 가 된다. If R ∼ Rice ( 0 , σ ) {\displaystyle R\sim \operatorname {Rice} (0,\sigma )} R ∼ Rayleigh ( σ ) {\displaystyle R\sim \operatorname {Rayleigh} (\sigma )} ν = 0 {\displaystyle \nu =0} Rayleigh distribution , for which the varian ce는 μ2 4 σ 2 {\ displaystyle \mu _{2}={\frac {4-\pi }{2}}\sigma ^{2 R 쌀 0 σ {\displaystyle R\sim \operatorname {Rice} (0,\sigma )} 2 {\ displaystyle ^{2}}: 지수분포를 .[6] R 쌀 ν σ {\ displaystyle R\sim \operatorname {Rice} \left(\nu ,\sigma rigma )} R displaystystylean /R} [7] 접힌 정규 분포 는 라이스 분포의 일변량 특례다.사례 제한 인수의[8]
임이 있는 x → − ∞ L ν ( x ) = x ν Γ ( 1 + ν ) . {\displaystyle \lim _{x\오른쪽 화살표 -\puty }L_{\nu }(x)={\frac {x^{\nu }}}{\감마(1+\nu )}}}. } ν 이 커지거나 σ이 작아지면 평균은 ν 이 되고 분산이 σ이2 되는 것으로 보인다.
가우스 근사치로의 전환은 다음과 같이 진행된다. 베셀 함수 이론에서 우리는
I α ( z ) → e z 2 π z ( 1 − 4 α 2 − 1 8 z + ⋯ ) 로서 z → ∞ {\displaystyle I_{\alpha }(z)\오른쪽 화살표 {\frac{e^{z}}{\sqrt{2\pi z}}\왼쪽(1-{\frac {4\alpha^{2}-1}{8z+\cdots \오른쪽){}\text{}}}}} 따라서 큰 x ν σ {\ displaystyle x\nu /\sigma ^{2}}개
f ( x , ν , σ ) = x σ 2 생략하다 ( − ( x 2 + ν 2 ) 2 σ 2 ) I 0 ( x ν σ 2 ) 이다 x σ 2 생략하다 ( − ( x 2 + ν 2 ) 2 σ 2 ) σ 2 2 π x ν 생략하다 ( 2 x ν 2 σ 2 ) ( 1 + σ 2 8 x ν + ⋯ ) → 1 σ 2 π 생략하다 ( − ( x − ν ) 2 2 σ 2 ) x ν , 로서 x ν σ 2 → ∞ {\displaystyle {\regated}f(x,\nu,\fracema )={}&{{\frac {x}{2}}\exp \leftleft\frac {-(x^{2}+\nu ^{2}}}}}{2\ma ^2}}\오른쪽) I_{0}\왼쪽({\frac {x\nu }{\sigma ^{2}}\오른쪽) \\{\text{은}}\\&,{\frac{)}{\sigma ^{2}}}\exp \left({\frac{-(x^{2}+\nu^{2})}{2\sigma ^{2}}}\right){\sqrt{\frac{\sigma ^{2}}{2\pi x\nu}}}\exp \left({\frac{2x\nu}{2\sigma ^{2}}}\right)\left(1+{\frac{\sigma ^{2}}{8x\nu}}+\cdots \right)\\\rightarrow{}&,{\frac{1}{\sigma{\sqrt{2\pi}}}}\exp}\left(-{\frac{())^{2}{2\sigma ^{2}.}}\right ){\sqrt{\frac {x}{\nu}}}}\;\;\\\\텍스트{{}}{\frac {x\nu }{\frac {x\nu }{\}}{\prow \flined}}}}}} 더구나 가우스 지수로 인해ν {\textstyle \nu x ν ≪ σ textstyle x-\nu \ll } ν 1 {\displaystystyle {\x}{x nu}\}\}\}\}}\}\}}}}}}\c
f ( x , ν , σ ) ≈ 1 σ 2 π 생략하다 ( − ( x − ν ) 2 2 σ 2 ) , ν σ ≫ 1 {\displaystyle f(x,\nu,\pima )\tx{\frac {1}{\frac {\sqrt{2\pi }}}}}\exp \frac{{2\frac ^{2}}\}\;\\frac {}{{{\nu}}}}\g} 근사치는 ν 3 {\displaystyle {\frac {\nu sigma }} .
모수 추정(코이 반전 기법) 쌀 분포의 모수를 추정하는 방법에는 세 가지 방법 ,[9] [10] [11] [12] 모멘트 방법 , (2) [9] [10] [11] [13] [citation needed 처음 두 방법에서 관심사는 데이터 표본으로부터 분포의 모수인 and과 estimating을 추정하는 것이다. 이것은 예를 들어 표본 평균 및 표본 표준 편차와 같은 모멘트의 방법을 사용하여 수행할 수 있다. 표본 평균은 μ의1 ' 추정치, 표본 표준 편차는 μ의2 1/2 추정치다.
다음은 "Koay 반전 기법"으로 알려진 효율적인 방법이다.[14] 표본 평균과 표본 표준 편차에 기초하여 동시에 추정 방정식을 푸는 경우. 이 반전 기법은 SNR 의 고정점 공식으로도 알려져 있는데, 이전의 순간의 방법에 관한 작품들은[9] [15]
먼저 표본표준편차에 대한 표본평균의 비율은 r , 즉 μ μ 2 2 {\ displaystyle r=\mu _{1}^{'}/\mu _{2}^{1/2}}. .
g ( θ ) = ξ ( θ ) [ 1 + r 2 ] − 2 , {\displaystyle g(\theta )={\sqrt {\xi {(\theta )}\왼쪽[1+r^{2}\오른쪽]-2,},} 여기서θ {\displaystyle \theta} = ν σ \ \frac {\nu }{\sigma }}, ξ \ xi {\reft(\ta \teft
ξ ( θ ) = 2 + θ 2 − π 8 생략하다 ( − θ 2 / 2 ) [ ( 2 + θ 2 ) I 0 ( θ 2 / 4 ) + θ 2 I 1 ( θ 2 / 4 ) ] 2 , {\displaystyle \xi {\reft(\theta \right)}=2+\theta ^{2}-{\frac {\pi }}}}\exp {(-\theta ^{2}/2)}\좌측[(2+\ta ^{2})} I_{0}(\theta ^{2}/4)+\theta ^{2} I_{1}(\theta ^{2}/4)\right]^{2},} 여기서 I 0 {\ displaystyle I_{0} I 1 {\ displaystyle I_{1 번째 종류의 Besel 함수를 수정 한다
ξ(θ ){\ displaystyle \xi {\좌(\theta \오른쪽)}}} displaystyle \sigma } μ2 {\ displaystyle \mu_{2
μ 2 = ξ ( θ ) σ 2 . {\displaystyle \mu _{2}=\xi {\\reft(\theta \rift)(\theta \right)}\ftma ^{2}.\,} To find the fixed point, θ ∗ {\displaystyle \theta ^{*}} g {\displaystyle g} θ 0 {\displaystyle {\theta }_{0}} θ l o w e r b o u n d = 0 {\displaystyle {\theta }_{\mathrm {lowerbound} }=0} r = π 4 π ){\ displaystyle ={\sqrt {\pi (4-\pi )}}}}( [14] 이것 μ 1 μ 2 {\ displaysty r=\mu _{1}^{ 1/2}} 이것은 기능 구성을 사용하는 반복에 대한 출발점을 제공하며,[clarification needed 이는 gi θ 0 i 1 {\ displaystyle \left ^{i}\좌측(\theta _{0}\오른쪽)-\theta _{i-1}\우측 }} 여기서 g i {\ displaystyle ^{i} 함수 {\displaystyle g i {\displaystyle } 실제로 일부 정수 n {\displaystyle n} θn {\ displaystyle \theta _{n} θ ∗{\ displaystyle \theta ^{*}}, θ g ( ta ^{*}\오른쪽) .
고정점을 찾으면 다음과 같이 스케일링 함수인 ξ(θ ){\ displaystyle \nu } {\displaystyle \ sigma }} ( ν{\ displaystystyle xi {\\refteft \tep
σ = μ 2 1 / 2 ξ ( θ ∗ ) , {\displaystyle \frac {\mu _{2}^{1/2}}{\sqrt {\xi \i \left(\ta ^{*}\오른쪽)}}}}, 그리고
ν = ( μ 1 ′ 2 + ( ξ ( θ ∗ ) − 2 ) σ 2 ) . {\displaystyle \nu ={\sqrt}\\\ft(\mu_{1}^{1}~2}+\ft(\xi \xi \left)(\theta ^{*}\right)\putma ^{2}\right}}}}}}. } 반복 속도를 더욱 높이기 위해 뉴턴의 뿌리 찾기 방법을 사용할 수 있다.[14] 이 특별한 접근법은 매우 효율적이다.
적용들 참고 항목 참조 ^ A.와 Tepedelenlioglu, C.와 Kaveh, M. 및 Giannakis, G., "쌀 퇴색 분포에 대한 K 매개변수 추정에 관하여 ", IEEE Communications Letters , 2001년 3월, 페이지 92–94 ^ Lui 2007(Horn의 결합초기하 함수 중 하나에서 두 변수). ^ 안나말라이 2000(무한계열의 합계). ^ 에르데일리 1953년 ^ 스리바스타바 1985년 ^ Richards, M.A., RCS를 위한 쌀 배급 (2006년 9월) ^ 존스, 제시카 L, 조이스 맥러플린, 다니엘 렌지. "고정된 공간 위치에서 도착 시간을 사용하여 계산한 전단파 속도 영상의 소음 분포.", 역 문제 33.5(2017): 055012. ^ 아브라모위츠와 스테건(1968년) §13 .5.1 ^ a b c 탈룩다르 외 1991년 ^ a b 보니 외 1996년 ^ a b 시버스 외 1998년 ^ 2014년 데커와 시버스 ^ 바라다라얀과 할다르 2015 ^ a b c Koay et al. 2006(SNR 고정 포인트 공식으로 알려져 있다). ^ 압디 2001 ^ "Ballistipedia" . Retrieved 4 May 2014 .^ Beaulieu, Norman C; Hemachandra, Kasun (September 2011). "Novel Representations for the Bivariate Rician Distribution". IEEE Transactions on Communications . 59 (11): 2951–2954. doi :10.1109/TCOMM.2011.092011.090171 . ^ Dharmawansa, Prathapasinghe; Rajatheva, Nandana; Tellambura, Chinthananda (March 2009). "New Series Representation for the Trivariate Non-Central Chi-Squared Distribution" (PDF) . IEEE Transactions on Communications . 57 (3): 665–675. CiteSeerX 10.1.1.582.533 doi :10.1109/TCOMM.2009.03.070083 .
추가 읽기 아브라모위츠, M., 스테건, I. A. (edd.), 수학적 기능 핸드북 , 국가표준국, 1964; 도버 출판물, 1965. ISBN 0-486-61272-4 쌀, S. O. 수학적 무작위 소음 분석 Bell System Technical Journal 24 (1945) 46–156. I. Soltani Bozchalooi and Ming Liang (20 November 2007). "A smoothness index-guided approach to wavelet parameter selection in signal de-noising and fault detection". Journal of Sound and Vibration . 308 (1–2): 253–254. Bibcode :2007JSV...308..246B . doi :10.1016/j.jsv.2007.07.038 . {{cite journal }}: CS1 maint: 작성자 매개변수 사용(링크 ) Wang, Dong; Zhou, Qiang; Tsui, Kwok-Leung (2017). "On the distribution of the modulus of Gabor wavelet coefficients and the upper bound of the dimensionless smoothness index in the case of additive Gaussian noises: Revisited". Journal of Sound and Vibration . 395 : 393–400. doi :10.1016/j.jsv.2017.02.013 . Liu, X. and Hanzo, L., A Unified Exact BER Performance Analysis of Asynchronous DS-CDMA Systems Using BPSK Modulation over Fading Channels , IEEE Transactions on Wireless Communications, Volume 6, Issue 10, October 2007, pp. 3504–3509. Annamalai, A., Tellambura, C. and Bhargava, V. K., Equal-Gain Diversity Receiver Performance in Wireless Channels , IEEE Transactions on Communications,Volume 48, October 2000, pp. 1732–1745. Erdelyi, A., Magnus, W., Oberhettinger, F. and Tricomi, F. G., Higher Transcendental Functions, Volume 1. McGraw-Hill Book Company Inc., 1953. Srivastava, H. M. and Karlsson, P. W., Multiple Gaussian Hypergeometric Series. Ellis Horwood Ltd., 1985. Sijbers J., den Dekker A. J., Scheunders P. and Van Dyck D., "Maximum Likelihood estimation of Rician distribution parameters" , IEEE Transactions on Medical Imaging, Vol. 17, Nr. 3, pp. 357–361, (1998) Varadarajan D. and Haldar J. P., "A Majorize-Minimize Framework for Rician and Non-Central Chi MR Images" , IEEE Transactions on Medical Imaging, Vol. 34, no. 10, pp. 2191–2202, (2015) den Dekker, A.J., and Sijbers, J (December 2014). "Data distributions in magnetic resonance images: a review". Physica Medica . 30 (7): 725–741. doi :10.1016/j.ejmp.2014.05.002 . PMID 25059432 . {{cite journal }}: CS1 maint: 작성자 매개변수 사용(링크 ) Koay, C.G. and Basser, P. J., Analytically exact correction scheme for signal extraction from noisy magnitude MR signals , Journal of Magnetic Resonance, Volume 179, Issue = 2, p. 317–322, (2006) Abdi, A., Tepedelenlioglu, C., Kaveh, M., and Giannakis, G. On the estimation of the K parameter for the Rice fading distribution , IEEE Communications Letters, Volume 5, Number 3, March 2001, pp. 92–94. Talukdar, K.K., and Lawing, William D. (March 1991). "Estimation of the parameters of the Rice distribution". Journal of the Acoustical Society of America . 89 (3): 1193–1197. Bibcode :1991ASAJ...89.1193T . doi :10.1121/1.400532 . {{cite journal }}: CS1 maint: 작성자 매개변수 사용(링크 ) Bonny,J.M., Renou, J.P., and Zanca, M. (November 1996). "Optimal Measurement of Magnitude and Phase from MR Data". Journal of Magnetic Resonance, Series B . 113 (2): 136–144. Bibcode :1996JMRB..113..136B . doi :10.1006/jmrb.1996.0166 . PMID 8954899 . {{cite journal }}: CS1 maint: 작성자 매개변수 사용(링크 ) 외부 링크
이산형 일변도의
연속 일변도의
의 지지를 받고 있는. 경계 간격 의 지지를 받고 있는. 반무한 간격을 두고 지지의 대체로 실선 지지하여 누구의 타입이 다른가.
혼합 일변도의
다변량 (공동) 방향 퇴보하다 그리고 단수 가족들












![{\displaystyle {\begin{aligned}\chi _{X}(t\mid \nu ,\sigma )=\exp \left(-{\frac {\nu ^{2}}{2\sigma ^{2}}}\right)&\left[\Psi _{2}\left(1;1,{\frac {1}{2}};{\frac {\nu ^{2}}{2\sigma ^{2}}},-{\frac {1}{2}}\sigma ^{2}t^{2}\right)\right.\\[8pt]&\left.{}+i{\sqrt {2}}\sigma t\Psi _{2}\left({\frac {3}{2}};1,{\frac {3}{2}};{\frac {\nu ^{2}}{2\sigma ^{2}}},-{\frac {1}{2}}\sigma ^{2}t^{2}\right)\right],\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78e23ca2a48dd2b11c2e5ca46a8f017950308c55)













 첫 번째 종류의
첫 번째 종류의 ![{\displaystyle {\begin{aligned}L_{1/2}(x)&=\,_{1}F_{1}\left(-{\frac {1}{2}};1;x\right)\\&=e^{x/2}\left[\left(1-x\right)I_{0}\left(-{\frac {x}{2}}\right)-xI_{1}\left(-{\frac {x}{2}}\right)\right].\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7baebb5240ced1a2464e31b42c0a0513eb18f296)









 (가) 다음과 같은 단계에서 발생하는 다른 사례:
(가) 다음과 같은 단계에서 발생하는 다른 사례:



 R
R 


















![g(\theta )={\sqrt {\xi {(\theta )}\left[1+r^{2}\right]-2}},](https://wikimedia.org/api/rest_v1/media/math/render/svg/3475731daba192c855cd90f039f3a56a2bc26321)


![\xi {\left(\theta \right)}=2+\theta ^{2}-{\frac {\pi }{8}}\exp {(-\theta ^{2}/2)}\left[(2+\theta ^{2})I_{0}(\theta ^{2}/4)+\theta ^{2}I_{1}(\theta ^{{2}}/4)\right]^{2},](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c016f1732f8a5a3bc72b406e9c40d7023f1f621)

 .
. 







 (가) 일부 작은 양의 값보다 작을 때까지 계속된다. 여기서
(가) 일부 작은 양의 값보다 작을 때까지 계속된다. 여기서 

 대한 최종
대한 최종  고정점으로,
고정점으로, 




