연속 베르누이 분포

연속 베르누이 분포

확률밀도함수
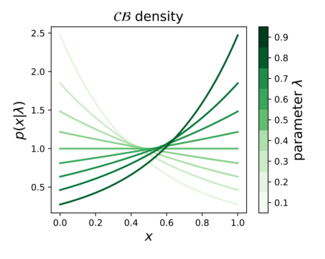표기법	${\displaystyle {\mathcal {CB}(\lambda )}$
매개변수	${\displaystyle \lambda \in (0,1)}$
지원	$[0,1]에서 [\displaystyle x\in]$
PDF	${\displaystyle C(\lambda )\lambda ^{x}(1-\lambda )^{1-x}\!}$ where ${\displaystyle C(\lambda )={\begin{cases}2&{\text{if }}\lambda ={\frac {1}{2}}\\{\frac {2\tanh ^{-1}(1-2\lambda )}{1-2\lambda }}&{\text{ otherwise}}\end{cases}}}$
CDF	${\displaystyle {\case}x&{\text{{}}}}}}{{\frac {1}{1}\frac {1}\practda ^{x}(1-\probda )^{1-x}+{2\probda -1}{{\text{\case}}}}}\}!}$
평균	${\displaystyle \operatorname {E} [X]={\begin{cases}{\frac {1}{2}}&{\text{ if }}\lambda ={\frac {1}{2}}\\{\frac {\lambda }{2\lambda -1}}+{\frac {1}{2\tanh ^{-1}(1-2\lambda )}}&{\text{ otherwise}}\end{cases}}\!}$
분산	${\displaystyle \operatorname {var} [X]={\begin{cases}{\frac {1}{12}}&{\text{ if }}\lambda ={\frac {1}{2}}\\{\frac {(1-\lambda )\lambda }{(1-2\lambda )^{2}}}+{\frac {1}{(2\tanh ^{-1}(1-2\lambda ))^{2}}}&{\text{ otherwise}}\end{cases}}\!}$

확률론, 통계학, 기계학습에서 연속 버누이 분포는^[1][2][3] 다음과 같이 단위간격 $x{\displaystyle }$ ${\displaystyle \in }$[ 0${\displaystyle }$, 1${\displaystyle }$) ${\$$displaystyle$ $\lambda \in (0$$,1)}$에 정의된 단일 형상변수 $\lambda {\displaystyle }$λ ($,$ 1)에 의해 매개변수화된 연속 $확률분포$ 계열이다$.$

${\displaystyle p(x \lambda )\propto \propto ^{x}(1-\{da )^{1-x}.}$

베르누이 분포는 딥러닝과 컴퓨터 비전, 특히 가변 자동 코더의 맥락에서 ^[4][5]자연 이미지의 픽셀 강도를 모델링하기 위해 발생한다.이와 같이, 연속적인 [${\displaystyle 0}$ ,${\displaystyle 1}$ {\$displaystyle [0,1]$ -값$$ 데이터에 종종 적용되는, 일반적으로 사용되는 이항 교차 엔트로피 손실에 대한 적절한 확률론적 대응책을 정의한다.^[6][7][8][9]2진수 교차 엔트로피 손실은 이산형${\displaystyle }${${\displaystyle 0}$, ${\displaystyle 1}$ ${\displaystyle \}}$ ${\displaystyle \{0,1\}}$ 값 데이터에$$ 대한 참 로그 우도만을 정의하기 때문에 이 관행은 연속적인 베르누이 분포의 정규화 상수를 무시하는 것이다.null

연속 베르누이는 또한 지수 분포의 집단을 정의한다.Writing ${\displaystyle \eta =\log \left(\lambda /(1-\lambda )\right)}$ for the natural parameter, the density can be rewritten in canonical form: ${\displaystyle p(x \eta )\propto \exp(\eta x)}$.

관련 분포

베르누이 분포

연속 베르누이는 확률 질량 함수에 의해$$ 이산형 집합${\displaystyle }${ 0${\displaystyle }$, ${\displaystyle 1}$ ${\displaystyle \}}$ ${\displaystyle \{0,1\}$에 정의된 베르누이 분포의 연속적인 이완으로 생각할 수 있다.

${\displaystyle p(x)=p^{x}(1-p)^{1-x}}$

여기서 $p{\displaystyle }$ ${\displaystyle p}$은(는) 0과 1 사이의 스칼라 파라미터다.이 동일한 기능 양식을 연속 간격${\displaystyle }$[ ${\displaystyle 0,}$ ${\displaystyle 1}$ ${\displaystyle ]}$ ${\displaystyle [0,1]}$에 적용하면 연속$$ 버누이 확률밀도 함수가 정규화 상수까지 된다.null

베타 분포

베타 분포에는 밀도 함수가 있다.

${\displaystyle p(x)\propto x^{\propto -1}(1-x)^{\property -1}$

다음과 같이 다시 쓸 수 있다.

${\displaystyle p(x)\propto x_{1}^{{1}^{1}-1x_{2}^{\property _{2}-1}}$

어디 α 1, α 2{\displaystyle \alpha_{1},\alpha _{2}}은 긍정적인 스칼라 매개 변수 및(x1x2){\displaystyle(x_{1},x_{2})}은 1-simplex 내부의 임의의 지점을 나타내는, Δ 1){(x1x2):x1>0x2>0x1+x2=1}{\displaystyle\Delta ^{1}=\{(.x_{1},$x_{2}:x_{1}>0,x_{2}>0,x_{1}+x_{2}=1$ 이 밀도 함수에서 매개 변수와 인수의 역할을 전환하여 다음을 얻는다.

${\displaystyle p(x)\propto \propto _{1}^{1}\properties _{2}^{x_{2}.}$

이 계열은 선형 제약 조건 ${\displaystyle {\alpha \mathrm{}}_{}}$ 1${\displaystyle {}_{}}$+ ${\displaystyle {\alpha \mathrm{}}_{}}$ 2${\displaystyle {}_{}}$= ${\displaystyle 1}$ ${\displaystyle \alpha _{1}+\alpha _{2}=1}$까지만 식별할 수 있으며$,$ 다음과 같은 경우:

${\displaystyle p(x)\propto \propto ^{x_{1}:{1}(1-\proda )^{x_{2}},}$

베르누이 밀도와 정확히 일치한다.null

지수 분포

단위 구간으로 제한된 지수 분포는 적절한 매개변수를 가진 연속 버누이 분포와 동일하다.null

연속 범주형 분포

연속 베르누이의 다변량 일반화를 연속 범주형이라고 한다.^[10]null

참조