스튜던트 t-검정

t-검정은 두 집단의 반응 간의 차이가 통계적으로 유의한지 여부를 검정하는 데 사용되는 통계적 가설 검정입니다. 검정 통계량이 귀무 가설 하에서 학생의 t-분포를 따르는 통계적 가설 검정입니다. 일반적으로 검정 통계량의 스케일링 항 값이 알려진 경우 검정 통계량이 정규 분포를 따르는 경우에 가장 일반적으로 적용됩니다(일반적으로 스케일링 항을 알 수 없으므로 성가신 모수임). 데이터를 기반으로 스케일링 항이 추정되면 특정 조건에서 검정 통계량이 학생의 t 분포를 따릅니다. t-검정의 가장 일반적인 적용은 두 모집단의 평균이 서로 다른지 여부를 검정하는 것입니다. 많은 경우 Z-검정은 데이터 세트의 크기가 증가함에 따라 후자가 전자로 수렴하기 때문에 t-검정과 매우 유사한 결과를 얻을 수 있습니다.

역사

"t-통계량"이라는 용어는 "가설 검정 통계량"에서 약칭됩니다.^[1] 통계학에서 t-분포는 1876년 Helmert와^[2][3][4] Lüroth에 의해 사후 분포로 처음 도출되었습니다.^[5][6][7] t-분포는 칼 피어슨(Karl Pearson)의 1895년 논문에서도 피어슨 유형 IV 분포로 보다 일반적인 형태로 나타났습니다.^[8] 그러나 Student's t-distribution이라고도 알려진 t-distribution은 윌리엄 실리 고셋(William Sealy Gosset)의 이름에서 따왔는데, 윌리엄의 고용주가 과학 논문을 출판할 때 직원들이 필명을 사용하는 것을 선호했기 때문에 1908년 과학 저널 바이오메트리카(Biometrika)에 "Student"^[9][10]라는 가명을 사용하여 처음 영어로 출판했습니다.^[11] 고셋은 아일랜드 더블린에 있는 기네스 양조장에서 일했고 작은 표본의 문제에 관심이 있었습니다. 예를 들어, 작은 표본 크기를 가진 보리의 화학적 특성. 따라서 학생이라는 용어의 어원의 두 번째 버전은 기네스가 경쟁자들이 원료의 품질을 결정하기 위해 t-검정을 사용하고 있다는 것을 알기를 원하지 않았다는 것입니다. 비록 "학생"이라는 용어가 쓰인 것은 윌리엄 고셋(William Gosset)이었지만, 이 분포가 "학생 분포"^[12]와 "학생 t-검정"으로 잘 알려지게 된 것은 사실 로널드 피셔(Ronald Fisher)의 작업을 통해서입니다.

고셋은 생화학과 통계를 기네스의 산업 공정에 적용하기 위해 옥스포드와 캠브리지에서 최고의 졸업생을 모집하는 클로드 기네스의 정책 덕분에 고용되었습니다.^[13] 고셋은 스타우트의 품질을 관찰하는 경제적인 방법으로 t-검정을 고안했습니다. t-테스트 작업은 바이오메트리카(Biometrika) 저널에 제출 및 승인되어 1908년에 출판되었습니다.^[9]

기네스는 1906-1907학년도 첫 두 학기 동안 University College London의 Carl Pearson 교수 생체 인식 연구소에서 기술 직원들이 공부를 위해 휴가를 낼 수 있도록 허용하는 정책(이른바 "스터디 휴가")을 가지고 있었습니다.^[14] 그 후 고셋의 정체는 동료 통계학자들과 칼 피어슨 편집장에게 알려졌습니다.^[15]

사용하다

가장 자주 사용되는 t-검정은 1-표본 및 2-표본 검정입니다.

• 모집단의 평균이 귀무 가설에서 지정된 값을 갖는지 여부에 대한 일표본 위치 검정.
• 두 모집단의 평균이 같다는 귀무 가설의 2-표본 위치 검정. 이러한 모든 검정을 일반적으로 스튜던트 t-검정이라고 하지만 엄밀히 말하면 두 모집단의 분산이 동일하다고 가정하는 경우에만 이 이름을 사용해야 합니다. 이 가정이 떨어졌을 때 사용되는 검정의 형태를 웰치 t-검정이라고 부르기도 합니다. 이러한 검정을 쌍을 이루지 않거나 독립적인 표본 t-검정이라고 하는 경우가 많은데, 이 검정은 일반적으로 비교되는 두 표본의 기초가 되는 통계 단위가 겹치지 않을 때 적용됩니다.^[16]

가정

^{[dubious – 토론]}

대부분의 검정 통계량은 t = Z/s의 형태를 가지며, 여기서 Z 및 s는 데이터의 함수입니다.

Z는 대안 가설(즉, 대안 가설이 참일 때 크기가 더 큰 경향이 있음)에 민감할 수 있지만, s는 t의 분포를 결정할 수 있는 스케일링 모수입니다.

예제: 일표본 t-검정에서

${\displaystyle t={\frac {Z}{s}}={\frac {\bar {X}-\mu}{\hat {\sigma }}/{\sqrt {n}}}$

여기서 X는 크기가 n인 표본 X, X, …, X의 표본 평균이고, s는 평균의 표준 오차이고,$$σ ^ {\$displaystyle$ {\hat {\sigma}}는 모집단의 표준 편차의 추정치이며, μ는 모집단 평균입니다.

위의 가장 간단한 형태의 t-검정의 기초가 되는 가정은 다음과 같습니다.

• X는 평균 μ 및 분산 σ/n을 갖는 정규 분포를 따릅니다.
• s(n - 1)/σ는 n - 1 자유도를 갖는 χ 분포를 따릅니다. 이² 가정은 추정에 사용되는 관측치가 정규 분포(그리고 각 그룹에 대한 정규 분포)에서 나올 때 충족됩니다.
• Z와 s는 독립적입니다.

두 독립 표본의 평균을 비교하는 t-검정에서는 다음과 같은 가정을 충족해야 합니다.

• 비교되는 두 모집단의 평균은 정규 분포를 따라야 합니다. 약한 가정 하에서 이는 각 그룹의 관측치 분포가 정규 분포가 아닌 경우에도 중심 한계 정리의 큰 표본에서 따릅니다.^[17]
• t-검정에 대한 학생의 원래 정의를 사용하는 경우 비교되는 두 모집단의 분산이 같아야 합니다(F-검정, Levene 검정, Bartlett 검정 또는 Brown-Forsythe 검정을 사용하여 검정 가능, Q-Q 그림을 사용하여 그래픽으로 평가 가능). 비교되는 두 그룹의 표본 크기가 같으면 학생의 원래 t-검정은 분산이 동일하지 않을 때 매우 강건합니다.^[18] Welch의 t-검정은 표본 크기가 유사한지 여부에 관계없이 분산의 동일성에 민감하지 않습니다.
• 검정을 수행하는 데 사용된 데이터는 비교되는 두 모집단으로부터 독립적으로 표본을 추출하거나 완전 쌍을 이루어야 합니다. 이는 일반적으로 데이터에서 테스트할 수 없지만 데이터가 종속적인 것으로 알려진 경우(예: 검정 설계에 의해 쌍으로 구성됨) 종속 검정을 적용해야 합니다. 부분 쌍체 데이터의 경우 고전적인 독립 t-검정은 검정 통계량이 분포를 따르지 않을 수 있으므로 유효하지 않은 결과를 제공할 수 있는 반면 종속 t-검정은 쌍체화되지 않은 데이터를 버리기 때문에 최적이 아닙니다.^[19]

대부분의 2-표본 t-검정은 가정에서 큰 편차를 제외하고는 모두 강건합니다.^[20]

정확성을 위해 t-검정과 Z-검정에는 표본 평균의 정규성이 필요하고 t-검정에는 표본 분산이 척도화된 χ 분포를 따르며 표본 평균과 표본 분산이 통계적으로 독립적이어야 합니다. 이러한 조건을 충족하는 경우 개별 데이터 값의 정규성은 필요하지 않습니다. 중심 한계 정리에 의해 중간 크기의 표본 평균은 데이터가 정규 분포를 따르지 않더라도 정규 분포에 의해 잘 근사화됩니다. 비정규 데이터의 경우 표본 분산의 분포가 χ 분포에서 크게 벗어날 수 있습니다.

그러나 표본 크기가 크면 슬러츠키의 정리는 표본 분산의 분포가 검정 통계량의 분포에 거의 영향을 미치지 않는다는 것을 의미합니다. 즉, 샘플 크기 $n{\displaystyle }$ ${\displaystyle n}$이(가) 증가함에 따라:

${\displaystyle \sqrt{}\mathrm{n}(X}$ ${\displaystyle ¯\sqrt{}}$- μ) ${\displaystyle \to }$d${\displaystyle \sqrt{}{}^{}}$(0$σ$ 2)${\displaystyle {\sqrt {n}}({\bar$ {X$}-\mu)\xrightarrow {d}$ N(0,\sigma ^{2})}은 중앙 한계 정리에 따라,

${\displaystyle s^{}}$ ${\displaystyle 2^{}}$→ $σ$ 2 ${\displaystyle$s^{$2}\xrightarrow$igma$$^{2}}는 큰 수의 법칙에 따라,

${\displaystyle \therefore \frac{}{}}{\displaystyle n}$(${\displaystyle \frac{}{}}$ $¯$ - μ${\displaystyle )}$ ${\displaystyle \mathrm{s}}$ ${\displaystyle \to \mathrm{d}}$ N (0$,$ 1) ${\displaysty$frac ${\sqrt$ {$n}}({\bar$ {$X}-\$mu )}{$s}\xrightarrow {d}$N(0,1)}.

쌍체 및 쌍체 2-표본 t-검정

평균 차이에 대한 2-표본 t-검정에는 독립 표본(쌍체화되지 않은 표본) 또는 쌍체 표본이 포함됩니다. 쌍체 t-검정은 차단의 한 형태이며, 쌍체 단위가 비교되는 두 그룹의 구성원 자격과 무관한 "잡음 요인"(혼성자 참조)과 유사할 때 쌍체 t 검정보다 검정력(유형 II 오류를 피할 확률, 거짓 음성이라고도 함)이 더 큽니다.^[21] 다른 맥락에서 쌍체 t-검정을 사용하여 관측 연구에서 교란 요인의 영향을 줄일 수 있습니다.

독립적(쌍을 이루지 않은) 샘플

독립 표본 t-검정은 독립 표본과 동일하게 분포된 두 개의 개별 표본 집합을 얻을 때 사용되며 두 모집단 각각에서 한 개의 변수를 비교합니다. 예를 들어, 의학적 치료의 효과를 평가하고 100명의 피험자를 연구에 등록한 다음, 50명의 피험자를 치료 그룹에 무작위로 할당하고 50명의 피험자를 대조군에 할당한다고 가정합니다. 이 경우 두 개의 독립적인 표본이 있으며 쌍을 이루지 않은 t-검정 형태를 사용합니다.

짝을 이룬 표본

쌍체 표본 t-검정은 일반적으로 유사한 단위의 일치된 쌍의 표본 또는 두 번 검정된 단위의 한 그룹("반복 측정" t-검정")으로 구성됩니다.

반복 측정 t-검정의 대표적인 예는 고혈압의 경우와 같이 피험자를 치료하기 전에 검사하고 혈압 강하제를 사용하여 치료한 후에 동일한 피험자를 다시 검사하는 것입니다. 치료 전후의 동일한 환자 수를 비교함으로써 각 환자를 효과적으로 자신의 대조군으로 사용하고 있습니다. 이렇게 하면 귀무 가설의 올바른 기각(여기서는 처리에 의해 차이가 없음) 가능성이 훨씬 높아지며, 단순히 무작위 환자 간 변동이 제거되었기 때문에 통계적 검정력이 증가합니다. 그러나 통계적 검정력의 증가는 대가를 치르게 됩니다: 더 많은 검정이 필요하고 각 피험자는 두 번 검사를 받아야 합니다. 이제 표본의 절반이 나머지 절반에 의존하기 때문에 짝을 이룬 학생 t-검정의 n/2 - 1 자유도(n은 총 관측치 수)만 있습니다. 쌍은 개별 테스트 단위가 되며, 표본은 두 배로 증가해야 동일한 수의 자유도를 얻을 수 있습니다. 일반적으로 n - 1개의 자유도(n은 총 관측치 수)가 있습니다.^[22]

"일치-쌍 표본"을 기반으로 한 쌍 표본 t-검정은 쌍을 이루지 않은 표본의 결과이며, 이 표본은 이후에 관심 변수와 함께 측정된 추가 변수를 사용하여 쌍을 이루는 표본을 형성하는 데 사용됩니다.^[23] 매칭은 두 표본 각각에서 하나의 관측치로 구성된 값 쌍을 식별함으로써 수행되며, 쌍은 다른 측정 변수 측면에서 유사합니다. 이 접근법은 교락 요인의 영향을 줄이거나 제거하기 위해 관측 연구에서 때때로 사용됩니다.

쌍체 표본 t-검정은 흔히 "종속 표본 t-검정"이라고 합니다.

계산

다양한 t-검정을 수행하는 데 사용할 수 있는 명시적인 표현식은 아래와 같습니다. 각 경우에 귀무 가설 하에서 t-분포를 정확히 따르거나 근사하는 검정 통계량에 대한 공식이 제공됩니다. 또한, 각각의 경우에 적절한 자유도가 주어집니다. 이러한 각 통계량은 단일 꼬리 검정 또는 양측 꼬리 검정을 수행하는 데 사용할 수 있습니다.

t 값과 자유도가 결정되면 학생 t-분포의 값 표를 사용하여 p-값을 찾을 수 있습니다. 계산된 p-값이 통계적 유의성에 대해 선택된 임계값(일반적으로 0.10, 0.05 또는 0.01 수준)보다 작으면 귀무 가설은 반대 가설에 유리하게 기각됩니다.

일원 표본 t-검정

모집단 평균이 지정된 값 μ와₀ 같다는 귀무 가설을 검정할 때 통계량을 사용합니다.

${\displaystyle t={\frac{\bar {x}}-\mu _{0}}{s/{\sqrt {n}}}$

여기서 $x$¯ ${\displaystyle {\bar$ {x}}은 표본 평균이고, s는 표본 표준 편차이고 n은 표본 크기입니다. 이 테스트에 사용된 자유도는 n - 1입니다. 모집단이 정규분포를 따를 필요는 없지만 표본평균 $x$¯ {\$displaystyle {\bar$ {x$}}$의 모집단 분포는 정규분포를 따른다고 가정합니다.

중심 극한 정리에 의해 관측치가 독립적이고 두 번째 모멘트가 존재하는 경우 $t{\displaystyle }$ ${\displaystyle$ t$}$는 대략 정규 $N{\displaystyle (0;}$ ${\displaystyle 1)}$ ${\displaystyle$ N$(0;$ 1$)}$이 됩니다$.$

회귀선의 기울기

모형에 적합하다고 가정합니다.

${\displaystyle Y=\alpha +\beta x+\varepsilon,}$

여기서 x는 알려져 있고, α와 β는 알려지지 않았으며, ε는 평균이 0이고 분산 σ이 알려지지 않은 정규 분포 확률 변수이며, Y는 관심 있는 결과입니다. 기울기 β가 일부 지정된 값 β와₀ 같다는 귀무 가설을 검정하려고 합니다(종종 0으로 간주되며, 이 경우 귀무 가설은 x와 y가 상관이 없다는 것입니다).

허락하다

${\displaystyle {\begin{aligned}{\alpha}}, {\hat {\beta }&={\text{최소 squares 추정기}},\\SE_{\hat {\alpha}}, SE_{\hat {\beta }&={\text{최소 squares 추정기의 표준 오류}}를 표시합니다.\end{align}}}$

그리고나서

${\displaystyle t_{\text{score}}={\frac{\hat{\beta }}-\beta _{0}}{SE_{\hat {\beta }}}}\sim {\mathcal {T}}_{n-2}}$

귀무 가설이 참이면 n - 2 자유도를 갖는 t-distrib 분포를 갖습니다. 기울기 계수의 표준 오차:

${\displaystyle SE_{\hat {\beta }}={\frac {\displaystyle {\frac {1}{n-2}}\sum _{i=1}^{n}(y_{i}-{\hat {y}}_{i})^{2}}{\displaystyle \sum _{i=1}^{n}(x_{i}-{\bar {x}}^{2}}}$

잔차로 적을 수 있습니다. 허락하다

${\displaystyle {\begin{aligned}{\varepsilon}}_{i}&=y_{i}-{\hat {y}}_{i}=y_{i}-({\hat {\alpha}}+{\hat {\beta }x_{i})={\text{residuals}}={\text{추정 오류}},\\{\text{SSR}}&=\sum _{i=1}^{n}{\hat {\varepsilon}}_{i}}^{2}={\text{잔차 제곱의 합}}.\end{align}}}$

그러면_score t는 다음과 같이 주어집니다.

${\displaystyle t_{\text{score}}={\frac {({\hat {\beta }}-\beta _{0}){\sqrt {n-2}}{\frac {SSR}{\sum _{i=1}^{n}(x_{i}-{\bar {x}}^{2}}}}$

이것을_score 결정하는 또 다른 방법은

${\displaystyle t_{\text{score}}={\frac {r{\sqrt {n-2}}}{\sqrt {1-r^{2}}}$

여기서 r은 피어슨 상관 계수입니다.

t는_{score, intercept} t에서_{score, slope} 확인할 수 있습니다.

${\displaystyle t_{\text{score, intercept}}={\frac {\alpha }{\beta }}{\frac {t_{\text{score, slope}}{\sqrt {s_{\text{x}}^{2}+{\bar {x}}^{2}}}$

여기서_x² 는 표본 분산입니다.

독립 2-표본 t-검정

표본 크기 및 분산 동일

두 그룹(1, 2)이 주어진 경우, 이 테스트는 다음과 같은 경우에만 적용됩니다.

• 두 표본 크기가 같습니다.
• 두 분포의 분산이 동일하다고 가정할 수 있습니다.

이러한 가정의 위반에 대해서는 아래에서 논의합니다.

평균이 다른지 여부를 검정하는 t 통계량은 다음과 같이 계산할 수 있습니다.

${\displaystyle t={\frac {{\bar {X}}_{1}-{\bar {X}}_{2}}{s_{p}{\sqrt {\frac {2}{n}}}}},}$

어디에

${\displaystyle s_{p}={\sqrt {\frac {s_{X_{1}}^{2}+s_{X_{2}}^{2}}{2}}}.}$

여기는 n = n = n = n에 대한 합동 표준 편차이고 s와 s는 모집단 분산의 편향되지 않은 추정치입니다. t의 분모는 두 평균의 차이에 대한 표준 오차입니다.

유의성 검정의 경우 이 검정의 자유도는 2n - 2이며, 여기서 n은 표본 크기입니다.

표본 크기가 같거나 같지 않음, 분산이 유사함(1_X1/2 < s/s_X2 < 2)

이 검정은 두 분포의 분산이 동일하다고 가정할 수 있는 경우에만 사용됩니다(이 가정이 위배될 때는 아래를 참조하십시오). 이전 공식들은 아래 공식들의 특별한 경우이며, 두 샘플의 크기가 같을 때 하나는 n = n = n 이 됩니다.

평균이 다른지 여부를 검정하는 t 통계량은 다음과 같이 계산할 수 있습니다.

${\displaystyle t={\frac {{\bar {X}}_{1}-{\bar {X}}_{2}}{s_{p}\cdot {\sqrt {{\frac {1}{n_{1}}}+{\frac {1}{n_{2}}}}}}},}$

어디에

${\displaystyle s_{p}={\sqrt {\frac {(n_{1}-1)s_{X_{1}}^{2}+(n_{2}-1)s_{X_{2}}^{2}}{n_{1}+n_{2}-2}}}}$

두 표본의 합동 표준 편차는 모집단 평균이 동일한지 여부에 관계없이 제곱이 공통 분산의 편향되지 않은 추정치가 되도록 이러한 방식으로 정의됩니다. 이 공식에서 n_i - 1은 각 그룹의 자유도 수이고 총 표본 크기에서 2를 뺀 값(즉, n₁ + n₂ - 2)은 유의성 검정에 사용되는 총 자유도 수이다.

표본 크기가 같거나 같지 않음, 분산이 같지 않음(s_X1X2 > 2s_X2 또는 s > 2s_X1)

Welch의 t-검정이라고도 하는 이 검정은 두 모집단 분산이 동일하다고 가정되지 않을 때만 사용되며(두 표본 크기가 동일할 수도 있고 그렇지 않을 수도 있음), 따라서 별도로 추정해야 합니다. 모집단 평균이 다른지 여부를 검정하는 t 통계량은 다음과 같이 계산됩니다.

${\displaystyle t={\frac {{\bar {X}}_{1}-{\bar {X}}_{2}}{s_{\bar {\Delta }}}},}$

어디에

${\displaystyle s_{\bar {\Delta }}={\sqrt {{\frac {s_{1}^{2}}{n_{1}}}+{\frac {s_{2}^{2}}{n_{2}}}}}.}$

여기에는 그룹 i의 참가자 수가 n = 1 또는 2인 두 표본 각각의 분산에 대한 편향되지 않은 추정치가 있습니다. 이 경우$({\displaystyle {}_{}}$δ ¯) 2 {\$displaystyle$(s_${\bar${\Delta }})^{2}}는 풀링된 분산이 아닙니다. 유의성 검정에 사용하기 위해 검정 통계량의 분포는 다음을 사용하여 계산된 자유도와 함께 일반 학생의 t-분포로 근사화됩니다.

${\displaystyle {\text{d.f.}}={\frac {\left({\frac {s_{1}^{2}}{n_{1}}}+{\frac {s_{2}^{2}}{n_{2}}}\right)^{2}}{{\frac {(s_{1}^{2}/n_{1})^{2}}{n_{1}-1}}+{\frac {(s_{2}^{2}/n_{2})^{2}}{n_{2}-1}}}}.}$

이것은 웰치-새터스웨이트 방정식으로 알려져 있습니다. 검정 통계량의 실제 분포는 알 수 없는 두 모집단 분산(Behrens–Fisher 문제 참조)에 따라 다릅니다.

동일하지 않은 분산 및 표본 크기에 대한 정확한 방법

이^[24] 검정은 유명한 베렌스-피셔 문제를 다루는데, 즉 두 모집단의 분산이 동일하지 않다고 가정할 때 두 정규 분포 모집단의 평균 간의 차이를 두 개의 독립적인 표본을 기반으로 비교합니다.

이 검정은 두 모집단의 동일하지 않은 표본 크기와 동일하지 않은 분산을 허용하는 정확한 검정으로 개발됩니다. 매우 작고 불균형한 표본 크기(${\displaystyle {예}_{}}$: n 1 = ${\displaystyle 5,{}_{}}$n $2$ = 50 {\displaystyle n_{1} = 5, n_{2} = 50})에서도 정확한 속성이 유지됩니다.

평균이 다른지 여부를 검정하는 통계량은 다음과 같이 계산할 수 있습니다.

$X$ =${\displaystyle }$[${\displaystyle {}_{}}$ $,$ X 2, …, X $m$] T {\displaystyle X = [X_{1}, X_{2},\ldots, X_{m}]^${T}}$ 및 $Y$ $=$${\displaystyle }$[${\displaystyle Y_{}}$ 1$,$ Y 2, …, $Y$] T {\displaystyle Y $=$ [Y_{1}, Y_{2},\ldots,Y_{n}]^${T}}$ be the i.i.d. sample vectors (${\displaystyle m\geq n}$) from ${\displaystyle N(\mu _{1},\sigma _{1}^{2})}$ and ${\displaystyle N(\mu _{2},\sigma _{2}^{2})}$ separately.

$({\displaystyle {PT}^{}{}_{}}$ ${\displaystyle n_{}}$× ${\displaystyle n_{}}$ ${\$ n$}}$라고 하자. 첫 번째 행의 $요소$가 모두 1${\displaystyle /n\sqrt{}}${\$displaystyle 1/{\sqrt$ {n$}}$인 $n{\displaystyle }$×$$ {\$times$n} 직교$$ 행렬이라고 하자$.$ 마찬가지로, $({\displaystyle {}^{}}$ ${\displaystyle T^{}{}_{}}$ ${\displaystyle n_{}}$× m ${\$ m$}$를 m${\displaystyle }$× ${\displaystyle m}$ ${\displaystyle$ m$\times m}$ 직교$$ 행렬의 첫 번째 n행(첫 번째 행의 요소는 모두 $1{\displaystyle \mathrm{}}$/ ${\displaystyle m\sqrt{}}$ ${\$이라고 합니다.$$

$그러면$ $Z$:= ${\displaystyle (Q^{}}$ T$)$ n × m X / m - (PT) n × n Y / n {\displaystyle Z:= (Q^{T})_{n\times m}X/{\sqrt {m}-(P^{T})_{n\times n}Y/{\sqrt {n}}는 n차원 정규 랜덤 벡터입니다.

${\displaystyle Z\sim N((\mu _{1}-\mu _{2},0,...,0)^{T},(\sigma _{1}^{2}/m+\sigma _{2}^{2}/n)I_{n}).}$

위의 분포로부터 우리는 다음과 같은 것을 알 수 있습니다.

${\displaystyle Z_{1}={\bar {X}}-{\bar {Y}}={\frac {1}{m}}\sum _{i=1}^{m}X_{i}-{\frac {1}{n}}\sum _{j=1}^{n}Y_{j}}$

${\displaystyle Z_{1}-(\mu _{1}-\mu _{2})\sim N(0,\sigma _{1}^{2}/m+\sigma _{2}^{2}/n),}$

${\displaystyle {\frac {\sum _{i=2}^{n}Z_{i}^{2}}{n-1}}\sim {\frac {\chi _{n-1}^{2}}{n-1}}\times \left({\frac {\sigma _{1}^{2}}{m}}+{\frac {\sigma _{2}^{2}}{n}}\right)}$

${\displaystyle Z_{1}-(\mu _{1}-\mu _{2})\perp \sum _{i=2}^{n}Z_{i}^{2}.}$

${\displaystyle T_{e}:={\frac {Z_{1}-(\mu _{1}-\mu _{2})}{\sqrt {(\sum _{i=2}^{n}Z_{i}^{2})/(n-1)}}}\sim t_{n-1}.}$

쌍체 표본에 대한 종속 t-검정

이 테스트는 샘플이 종속적인 경우, 즉 두 번 테스트된 샘플이 하나뿐인 경우(반복 측정) 또는 일치하거나 "짝짓기"된 샘플이 두 개인 경우에 사용됩니다. 쌍체 차이 검정의 예입니다. t 통계량은 다음과 같이 계산됩니다.

${\displaystyle t={\frac {{\bar {X}}_{D}-\mu _{0}}{s_{D}/{\sqrt {n}}}},}$

${\displaystyle {여기}_{}}$서 $X$¯ D${\displaystyle {\bar${X}_{$D$} $s$ D ${\displaystyle$ s_{D}}는 모든 쌍 간 차이의 평균 및 표준 편차입니다. 쌍은 예를 들어, 한 사람의 사전 테스트 및 사후 테스트 점수 또는 의미 있는 그룹(예를 들어, 동일한 가족 또는 연령 그룹에서 추출됨: 표 참조)으로 일치하는 사람들 간의 쌍입니다. 차이의 평균이 유의하게 다른지 검정하려면 상수 μ가₀ 0입니다. 사용된 자유도는 n - 1이며, 여기서 n은 쌍의 수를 나타냅니다.

일치하는 쌍의 예제 짝 이름. 나이 시험 1 존. 35 250 1 제인. 36 340 2 지미. 22 460 2 제시 21 200

반복 측정 예제 번호 이름. 테스트1 테스트 2 1 마이크 35% 67% 2 멜라니 50% 46% 3 멜리사 90% 86% 4 미첼 78% 91%

작업예

이 기사는 해당 메인 기사를 더 잘 요약해야 할 수도 있습니다. 요약을 개선하는 데 도움을 주세요. (이 템플릿 메시지를 제거하는 방법과 시기에 대해 알아보세요.)

A를₁ 6개 측정값의 임의표본을 그려서 얻은 집합이라고 합니다.

${\displaystyle A_{1}=\{30.02,\29.99,\30.11,\29.97,\30.01,\29.99\}$

그리고₂ A를 유사하게 구한 두 번째 집합이라고 합니다.

${\displaystyle A_{2}=\{29.89,\29.93,\29.72,\29.98,\30.02,\29.98\}$

예를 들어, 이것들은 두 개의 다른 기계에 의해 제조된 나사의 무게일 수 있습니다.

두 표본을 추출한 모집단의 평균이 같다는 귀무 가설의 검정을 수행합니다.

위에서 설명한 모든 두 표본 검정 방법에 대한 분자에 나타나는 X로_i 표시된 두 표본 평균의 차이는 다음과 같습니다.

${\displaystyle {\bar {X}}_{1}-{\bar {X}}_{2}=0.095.}$

두 표본에 대한 표본 표준 편차는 각각 약 0.05와 0.11입니다. 이러한 작은 표본의 경우 두 모집단 분산 간의 동일성 검정은 그다지 강력하지 않습니다. 표본 크기가 같기 때문에 이 예제에서는 두 표본 t-검정의 두 가지 형태가 유사하게 수행됩니다.

부등분산

위에서 설명한 동일하지 않은 분산에 대한 접근 방식을 따르는 경우 결과는 다음과 같습니다.

${\displaystyle {\sqrt {{\frac {s_{1}^{2}}{n_{1}}}+{\frac {s_{2}^{2}}{n_{2}}}}}\approx 0.04849}$

그리고 자유도.

${\displaystyle {\text{d.f.}}\approx 7.031.}$

검정 통계량은 약 1.959이며, 양측 검정 p-값은 0.09077입니다.

등분산

등분산에 대한 접근법(위에서 설명한)을 따를 경우 결과는 다음과 같습니다.

${\displaystyle s_{p}\approx 0.08396}$

그리고 자유도.

${\displaystyle {\text{d.f.}}=10.}$

검정 통계량은 대략 1.959이며, 이는 양측 p-값 0.07857을 제공합니다.

관련 통계시험

위치 문제에 대한 t-검정의 대안

t-검정은 분산이 동일하지만 알려지지 않은 두 i.d. 정규 모집단의 평균의 동일성에 대한 정확한 검정을 제공합니다. (Welch의 t-검정은 데이터가 정규 분포를 따르지만 분산이 다를 수 있는 경우에 대한 거의 정확한 검정입니다.) 중간 크기의 표본과 단일 꼬리 검정의 경우 t-검정은 정규성 가정의 중간 위반에 대해 비교적 강력합니다.^[25] 충분히 큰 표본에서 t-검정은 z-검정에 점근적으로 접근하고 정규성에서 큰 편차에도 강건해집니다.^[17]

데이터가 상당히 비정규적이고 표본 크기가 작으면 t-검정은 잘못된 결과를 제공할 수 있습니다. 비정규 분포의 특정 계열과 관련된 일부 이론에 대한 가우스 척도 혼합 분포의 위치 검정을 참조하십시오.

정규성 가정이 성립하지 않을 때 t-검정에 대한 비모수적 대안이 더 나은 통계적 검정력을 가질 수 있습니다. 그러나 데이터가 그룹 간 분산이 다른 비정규 분포를 따르는 경우 t-검정은 일부 비모수적 대안보다 유형-1 오차 관리가 더 우수할 수 있습니다.^[26] 또한 아래에서 설명하는 Mann-Whitney U 검정과 같은 비모수적 방법은 일반적으로 평균의 차이를 검정하지 않으므로 평균의 차이가 주요 과학적 관심사인 경우 주의해서 사용해야 합니다.^[17] 예를 들어, Mann-Whitney U 검정은 두 그룹의 분포가 같은 경우 유형 1 오차를 원하는 수준의 알파로 유지합니다. 또한 그룹 B가 A와 동일한 분포를 갖지만 상수로 약간 이동한 후에 (이 경우 두 그룹의 평균에 실제로 차이가 있을 수 있음) 다른 방법을 탐지하는 데에도 힘이 있습니다. 그러나 그룹 A와 B가 서로 다른 분포를 갖지만 동일한 평균(예: 두 분포, 하나는 양의 왜도를 갖지만 다른 하나는 음의 분포를 갖지만 동일한 평균을 갖도록 이동)을 갖는 경우가 있을 수 있습니다. 이러한 경우 MW는 Null 가설을 기각하는 데 알파 수준 이상의 힘을 가질 수 있지만 평균 차이의 해석을 그러한 결과로 돌리는 것은 잘못된 것입니다.

이상치가 존재하는 경우 t-검정은 강건하지 않습니다. 예를 들어, 데이터 분포가 비대칭이거나(즉, 분포가 비대칭임) 분포의 꼬리가 큰 두 개의 독립적인 표본의 경우 Wilcoxon 순위 합 검정(만-휘트니 U 검정이라고도 함)은 t-검정보다 3~4배 높은 검정력을 가질 수 있습니다.^[25][27][28] 쌍체 표본 t-검정의 비모수 대응물은 쌍체 표본에 대한 Wilcoxon 부호 순위 검정입니다. t-검정과 비모수 대안 중 하나를 선택하는 방법에 대한 자세한 내용은 Lumley 등을 참조하십시오. (2002).^[17]

일원 분산 분석(ANOVA)은 데이터가 두 개 이상의 그룹에 속할 때 2-표본 t-검정을 일반화합니다.

쌍체 관측치와 독립 관측치를 모두 포함하는 설계

쌍체 관측치와 독립 관측치가 모두 두 표본 설계에 존재할 때, 데이터가 무작위로 완전히 누락되었다고 가정하면, 쌍체 관측치 또는 독립 관측치는 위의 표준 검정을 진행하기 위해 폐기될 수 있습니다. 또는 정규성 및 MCAR을 가정하여 사용 가능한 모든 데이터를 사용하여 일반화된 부분 중첩 표본 t-검정을 사용할 수 있습니다.^[29]

다변량 검정

주 기사: 호텔링의 T제곱 분포

학생의 t 통계량을 Hoteling의 t-제곱 통계량이라고 하는 일반화를 사용하면 동일한 표본 내에서 여러 개(종종 상관 관계가 있는) 측정치에 대한 가설을 검정할 수 있습니다. 예를 들어, 연구자는 여러 개의 성격 척도로 구성된 성격 검사(예: Minnesota Multiple Personality Inventory)에 여러 개의 피실험자를 제출할 수 있습니다. 이러한 유형의 측도는 일반적으로 양의 상관 관계가 있으므로, 측도 간의 공분산을 무시하고 적어도 하나의 가설(유형 I 오류)을 잘못 기각할 가능성을 높이기 때문에 가설을 검정하기 위해 별도의 일변량 t-검정을 수행하는 것은 바람직하지 않습니다. 이 경우 가설 검정에는 단일 다변량 검정이 좋습니다. 여러 검정과 검정 간의 양의 상관 관계에 대해 감소된 알파를 결합하는 Fisher's Method가 하나입니다. 다른 하나는 Hotelling의 T² 통계량이 T² 분포를 따른다는 것입니다. 그러나 실제로는² T에 대한 표 값을 찾기 어렵기 때문에 분포가 거의 사용되지 않습니다. 일반적으로 T는² F 통계량으로 변환됩니다.

일 표본 다변량 검정의 경우 평균 벡터(μ)가 주어진 벡터(μ₀)와 같다는 가설이 있습니다. 검정 통계량은 Hoteling의 t입니다².

${\displaystyle t^{2}=n({\bar {\mathbf {x} }}-{{\boldsymbol {\mu }}_{0}})'{\mathbf {S} }^{-1}({\bar {\mathbf {x} }}-{{\boldsymbol {\mu }}_{0}})}$

여기서 n은 표본 크기, x는 열 평균의 벡터, S는 m × m 표본 공분산 행렬입니다.

2-표본 다변량 검정의 경우, 가설은 두 표본의 평균₁ 벡터(μ₂, μ)가 같다는 것입니다. 검정 통계량은 Hotelling의 2-표본 t 검정입니다².

${\displaystyle t^{2}={\frac {n_{1}n_{2}}{n_{1}+n_{2}}\left({\bar {\mathbf {x}}}_{1}-{\bar {\mathbf {x}}}_{2}\right)'{\mathbf {S}_{\text{pooled}}^{-1}\left({\bar {\mathbf {x}}}-{\bar {\mathbf {x}}_{2}\right)}$

2-표본 t-검정은 단순 선형 회귀 분석의 특수한 경우입니다.

2-표본 t-검정은 다음 예제에서 보여주는 것처럼 단순 선형 회귀 분석의 특수한 경우입니다.

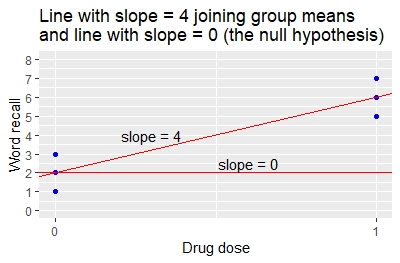
임상시험은 약물이나 위약을 투여받은 6명의 환자를 조사합니다. 3명의 환자는 0단위의 약(플라시보 그룹)을 얻습니다. 3명의 환자는 1단위의 약물(능동적 치료군)을 투여받습니다. 치료가 끝나면 연구원들은 각 환자가 기억력 검사에서 기억할 수 있는 단어 수의 기준선으로부터의 변화를 측정합니다.

R 프로그래밍 언어를 사용한 분석을 위한 데이터 및 코드가 다음과 같이 제공됩니다. t.test 그리고. lmt-검정 및 선형 회귀 분석에 대한 함수입니다. 다음은 R에서 생성된 (가상의) 데이터입니다.

> word.recall.data=data.frame(drug.dose=c(0,0,0,1,1,1), word.recall=c(1,2,3,5,6,7))

환자.	약.복용의	낱말.
1	0	1
2	0	2
3	0	3
4	1	5
5	1	6
6	1	7

t-검정을 수행합니다. 분석을 단순 선형 회귀 분석과 정확히 동일하게 하려면 등분산 가정 var.equal=T가 필요합니다.

> 와 함께(word. recall.데이터, t.시험을 보다(낱말.~약.복용의, 바아=T)) 

R 코드를 실행하면 다음과 같은 결과가 나옵니다.

• 0 drug.dose 그룹의 평균 단어.recall은 2입니다.
• 1개 약물.용량 그룹의 평균 단어는 6입니다.
• 평균 단어의 처리 그룹 간 차이 recall은 6 – 2 = 4입니다.
• 약물 용량 간의 단어 차이. recall이 유의합니다(p=0.00805).

동일한 데이터에 대한 선형 회귀 분석을 수행합니다. 계산은 R 함수를 사용하여 수행할 수 있습니다. lm() 선형 모델의 경우.

> 단어. recall.데이터. =  lm(낱말.~약.복용의, 데이터.=word. recall.데이터) > 요약(단어. recall.데이터.) 

선형 회귀 분석은 계수 및 p-값의 표를 제공합니다.

계수	추정	표준오류	t값	P값
가로채기	2	0.5774	3.464	0.02572
약.복용의	4	0.8165	4.899	0.000805

계수 표는 다음과 같은 결과를 제공합니다.

• 절편에 대한 추정치 2는 약물 용량이 0일 때 단어 회상의 평균값입니다.
• 약물 용량에 대한 추정치 4는 약물 용량의 1단위 변화(0에서 1까지)의 경우 평균 단어 회상(2에서 6까지)에 4단위 변화가 있음을 나타냅니다. 이것은 두 그룹 평균을 잇는 선의 기울기입니다.
• 기울기 4가 0과 다르다는 p-값은 p = 0.00805입니다.

선형 회귀 분석의 계수는 그래프와 같이 두 그룹 평균을 연결하는 선의 기울기와 절편을 지정합니다. 절편은 2이고 기울기는 4입니다.

선형 회귀 분석의 결과를 t-검정의 결과와 비교합니다.

• t-검정에서 그룹 평균 간의 차이는 6-2=4입니다.
• 회귀 분석에서 기울기도 4로 나타나 약물 용량의 1단위 변화(0에서 1까지)가 평균 단어 리콜의 4단위 변화(2에서 6까지)를 제공함을 나타냅니다.
• 평균 차이에 대한 t-검정 p-값과 기울기에 대한 회귀 p-값은 모두 0.00805입니다. 방법은 동일한 결과를 제공합니다.

이 예제는 값이 0과 1인 단일 x 변수가 있는 단순 선형 회귀 분석의 특수한 경우 t-검정이 선형 회귀 분석과 동일한 결과를 제공한다는 것을 보여줍니다. 관계는 대수적으로도 보여질 수 있습니다.

t-검정과 선형 회귀 사이의 이러한 관계를 인식하면 다중 선형 회귀 분석과 다변량 분산 분석을 쉽게 사용할 수 있습니다. 이러한 t-검정 대안을 사용하면 반응과 관련된 추가 설명 변수를 포함할 수 있습니다. 회귀 분석 또는 분산 분석을 사용하여 이러한 추가 설명 변수를 포함하면 그렇지 않으면 설명할 수 없는 분산이 줄어들고 일반적으로 두 표본 t-검정을 수행하는 것보다 차이를 탐지하는 검정력이 더 커집니다.

소프트웨어 구현

QtiPlot, LibreOffice Calc, Microsoft Excel, SAS, SPSS, Stata, DAP, gretl, R, Python, PSPP, Wolfram Mathematica, MATLAB 및 Minitab과 같은 많은 스프레드시트 프로그램 및 통계 패키지에는 Student's t-test의 구현이 포함되어 있습니다.

언어/프로그램	기능.	메모들
Microsoft Excel pre 2010	TTEST(array1, array2, tails, type)	[1] 참조
Microsoft Excel 2010 이상	T.TEST(array1, array2, tails, type)	[2] 참조
애플 넘버즈	TTEST(sample-1-values, sample-2-values, tails, test-type)	[3] 참조
리브르오피스칼	TTEST(Data1; Data2; Mode; Type)	[4] 참조
구글 시트	TTEST(range1, range2, tails, type)	[5] 참조
파이썬	scipy.stats.ttest_ind(a, b, equal_var=True)	[6] 참조
매트랩	ttest(data1, data2)	[7] 참조
마테마티카	TTest[{data1,data2}]	[8] 참조
R	t.test(data1, data2, var.equal=TRUE)	[9] 참조
SAS	PROC TTEST	[10] 참조
자바	tTest(sample1, sample2)	[11] 참조
줄리아.	EqualVarianceTTest(sample1, sample2)	[12] 참조
스타타	ttest data1 == data2	[13] 참조

참고 항목

• 조건변경모형
• F-검정 – 통계적 가설 검정, 대부분 여러 제약 조건을 사용함
• 검정력 분석의 비중심 t-분포 – 확률 분포
• 학생 t-통계 – 재연결 대상에 대한 짧은 설명을 표시하는 통계 페이지의 비율
• Z-검정 – 통계적 검정
• Mann-Whitney U 검정 – 귀무 가설의 비모수 검정
• t-검정에 대한 쉬다크 보정 – 통계적 방법
• Welch의 t-검정 – 두 모집단이 동일한 평균을 갖는지 여부에 대한 통계적 검정
• 분산 분석 – 통계 모형 수집(ANOVA)

참고문헌

1. ^ The Microbiome in Health and Disease. Academic Press. 2020-05-29. p. 397. ISBN 978-0-12-820001-8.
2. ^ Szabó, István (2003). "Systeme aus einer endlichen Anzahl starrer Körper". Einführung in die Technische Mechanik (in German). Springer Berlin Heidelberg. pp. 196–199. doi:10.1007/978-3-642-61925-0_16. ISBN 978-3-540-13293-6.
3. ^ Schlyvitch, B. (October 1937). "Untersuchungen über den anastomotischen Kanal zwischen der Arteria coeliaca und mesenterica superior und damit in Zusammenhang stehende Fragen". Zeitschrift für Anatomie und Entwicklungsgeschichte (in German). 107 (6): 709–737. doi:10.1007/bf02118337. ISSN 0340-2061. S2CID 27311567.
4. ^ Helmert (1876). "Die Genauigkeit der Formel von Peters zur Berechnung des wahrscheinlichen Beobachtungsfehlers directer Beobachtungen gleicher Genauigkeit". Astronomische Nachrichten (in German). 88 (8–9): 113–131. Bibcode:1876AN.....88..113H. doi:10.1002/asna.18760880802.
5. ^ Lüroth, J. (1876). "Vergleichung von zwei Werthen des wahrscheinlichen Fehlers". Astronomische Nachrichten (in German). 87 (14): 209–220. Bibcode:1876AN.....87..209L. doi:10.1002/asna.18760871402.
6. ^ Pfanzagl, J. (1996). "Studies in the history of probability and statistics XLIV. A forerunner of the t-distribution". Biometrika. 83 (4): 891–898. doi:10.1093/biomet/83.4.891. MR 1766040.
7. ^ Sheynin, Oscar (1995). "Helmert's work in the theory of errors". Archive for History of Exact Sciences. 49 (1): 73–104. doi:10.1007/BF00374700. ISSN 0003-9519. S2CID 121241599.
8. ^ Pearson, Karl (1895). "X. Contributions to the mathematical theory of evolution.—II. Skew variation in homogeneous material". Philosophical Transactions of the Royal Society of London A. 186: 343–414. Bibcode:1895RSPTA.186..343P. doi:10.1098/rsta.1895.0010.
9. ^ ^{a b} Student (1908). "The Probable Error of a Mean" (PDF). Biometrika. 6 (1): 1–25. doi:10.1093/biomet/6.1.1. hdl:10338.dmlcz/143545. Retrieved 24 July 2016.
10. ^ "T Table".
11. ^ Wendl, Michael C. (2016). "Pseudonymous fame". Science. 351 (6280): 1406. doi:10.1126/science.351.6280.1406. PMID 27013722.
12. ^ Walpole, Ronald E. (2006). Probability & statistics for engineers & scientists. Myers, H. Raymond (7th ed.). New Delhi: Pearson. ISBN 81-7758-404-9. OCLC 818811849.
13. ^ O'Connor, John J.; Robertson, Edmund F. "William Sealy Gosset". MacTutor History of Mathematics Archive. University of St Andrews.
14. ^ Raju, T. N. (2005). "William Sealy Gosset and William A. Silverman: Two 'Students' of Science". Pediatrics. 116 (3): 732–735. doi:10.1542/peds.2005-1134. PMID 16140715. S2CID 32745754.
15. ^ Dodge, Yadolah (2008). The Concise Encyclopedia of Statistics. Springer Science & Business Media. pp. 234–235. ISBN 978-0-387-31742-7.
16. ^ Fadem, Barbara (2008). High-Yield Behavioral Science. High-Yield Series. Hagerstown, MD: Lippincott Williams & Wilkins. ISBN 9781451130300.
17. ^ ^{a b c d} Lumley, Thomas; Diehr, Paula; Emerson, Scott; Chen, Lu (May 2002). "The Importance of the Normality Assumption in Large Public Health Data Sets". Annual Review of Public Health. 23 (1): 151–169. doi:10.1146/annurev.publhealth.23.100901.140546. ISSN 0163-7525. PMID 11910059.
18. ^ Markowski, Carol A.; Markowski, Edward P. (1990). "Conditions for the Effectiveness of a Preliminary Test of Variance". The American Statistician. 44 (4): 322–326. doi:10.2307/2684360. JSTOR 2684360.
19. ^ Guo, Beibei; Yuan, Ying (2017). "A comparative review of methods for comparing means using partially paired data". Statistical Methods in Medical Research. 26 (3): 1323–1340. doi:10.1177/0962280215577111. PMID 25834090. S2CID 46598415.
20. ^ Bland, Martin (1995). An Introduction to Medical Statistics. Oxford University Press. p. 168. ISBN 978-0-19-262428-4.
21. ^ Rice, John A. (2006). Mathematical Statistics and Data Analysis (3rd ed.). Duxbury Advanced.^{[ISBN 실종]}
22. ^ Weisstein, Eric. "Student's t-Distribution". mathworld.wolfram.com.
23. ^ David, H. A.; Gunnink, Jason L. (1997). "The Paired t Test Under Artificial Pairing". The American Statistician. 51 (1): 9–12. doi:10.2307/2684684. JSTOR 2684684.
24. ^ Wang, Chang; Jia, Jinzhu (2022). "Te Test: A New Non-asymptotic T-test for Behrens-Fisher Problems". arXiv:2210.16473 [math.ST].
25. ^ ^{a b} Sawilowsky, Shlomo S.; Blair, R. Clifford (1992). "A More Realistic Look at the Robustness and Type II Error Properties of the t Test to Departures From Population Normality". Psychological Bulletin. 111 (2): 352–360. doi:10.1037/0033-2909.111.2.352.
26. ^ Zimmerman, Donald W. (January 1998). "Invalidation of Parametric and Nonparametric Statistical Tests by Concurrent Violation of Two Assumptions". The Journal of Experimental Education. 67 (1): 55–68. doi:10.1080/00220979809598344. ISSN 0022-0973.
27. ^ Blair, R. Clifford; Higgins, James J. (1980). "A Comparison of the Power of Wilcoxon's Rank-Sum Statistic to That of Student's t Statistic Under Various Nonnormal Distributions". Journal of Educational Statistics. 5 (4): 309–335. doi:10.2307/1164905. JSTOR 1164905.
28. ^ Fay, Michael P.; Proschan, Michael A. (2010). "Wilcoxon–Mann–Whitney or t-test? On assumptions for hypothesis tests and multiple interpretations of decision rules". Statistics Surveys. 4: 1–39. doi:10.1214/09-SS051. PMC 2857732. PMID 20414472.
29. ^ Derrick, B; Toher, D; White, P (2017). "How to compare the means of two samples that include paired observations and independent observations: A companion to Derrick, Russ, Toher and White (2017)" (PDF). The Quantitative Methods for Psychology. 13 (2): 120–126. doi:10.20982/tqmp.13.2.p120.

원천

• O'Mahony, Michael (1986). Sensory Evaluation of Food: Statistical Methods and Procedures. CRC Press. p. 487. ISBN 0-82477337-3.
• Press, William H.; Teukolsky, Saul A.; Vetterling, William T.; Flannery, Brian P. (1992). Numerical Recipes in C: The Art of Scientific Computing. Cambridge University Press. p. 616. ISBN 0-521-43108-5.

더보기

• Boneau, C. Alan (1960). "The effects of violations of assumptions underlying the t test". Psychological Bulletin. 57 (1): 49–64. doi:10.1037/h0041412. PMID 13802482.
• Edgell, Stephen E.; Noon, Sheila M. (1984). "Effect of violation of normality on the t test of the correlation coefficient". Psychological Bulletin. 95 (3): 576–583. doi:10.1037/0033-2909.95.3.576.

외부 링크

Wikiversity에는 t-test에 대한 학습 자료가 있습니다.

• "Student test". Encyclopedia of Mathematics. EMS Press. 2001 [1994].
• Trochim, William M.K. "The T-Test", Research Methods Knowledge Base, conjoint.ly
• 마크 토마의 유튜브 계량경제학 강의(주제: 가설검정)