직선 및 나침반 구조
Straightedge and compass construction
| 기하학 |
|---|
 |
| 기하학 |
직선자와 나침반 구조는 자와 자로 이루어진 구조 또는 고전적인 구조로도 알려져 있으며, 이상적인 자와 나침반 한 쌍만을 사용하여 길이, 각도 및 기타 기하학적 형상을 구성한 것이다.
직선으로 알려진 이상화된 통치자는 길이가 무한하고 한쪽 가장자리만 있으며 그 위에 표시가 없는 것으로 추정된다. 나침반은 최대 또는 최소 반경이 없는 것으로 가정하며, 페이지에서 들어올릴 때 "붕괴"로 가정하므로 거리 전달에 직접 사용하지 않을 수 있다. (다단계 절차를 사용하면 나침반이 무너지더라도 거리가 이전될 수 있으므로 이것은 중요하지 않은 제한이다. 나침반 동등성 정리를 참조한다. 그러나 직선 가장자리에 고정된 충돌하지 않는 나침반은 표시와 같은 것처럼 보일 수 있지만, 네우시스 구조는 여전히 허용되지 않으며 이것이 표시되지 않은 진짜 의미라는 점에 유의하십시오. 아래 표시 가능한 통치자를 참조하십시오.) 좀 더 공식적으로, 유일한 건축은 유클리드 최초의 세 개의 시체가 허가한 것이다.
직선자와 나침반을 사용하여 구성할 수 있는 모든 점들은 나침반만을 사용하여 구성되거나, 하나의 원과 그 중심이 주어진다면 직선자만으로 구성될 수 있는 경우인 것으로 밝혀졌다.
고대 그리스 수학자들은 가장자리와 나침반 구조를 처음 구상했고, 평면 기하학에서 많은 고대 문제들이 이러한 제한을 가했다. 고대 그리스인들은 많은 건축물을 개발했지만, 어떤 경우에는 그렇게 할 수 없었다. Gauss는 일부 폴리곤은 구성 가능하지만 대부분은 그렇지 않다는 것을 보여주었다. 가장 유명한 직선 및 나침반 문제들 중 몇 가지는 1837년 피에르 원젤에 의해 수학적 분야 이론을 사용하여 불가능하다는 것이 입증되었다.
불가능하다는 기존의 증거에도 불구하고, 몇몇은 이러한 문제들을 해결하려고 계속 노력한다.[1] 다른 기하학적 변환이 허용된다면 이러한 많은 문제들은 쉽게 해결될 수 있다. 예를 들어, 큐브를 두 배로 늘리는 것은 기하학적 구조를 사용하여 가능하지만 직선자와 나침반만으로는 가능하지 않다.
대수적으로, 길이는 그것이 구성 가능한 숫자를 나타내는 경우에만 구성 가능하며, 각도는 그것의 코사인이 구성 가능한 숫자인 경우에만 구성 가능하다. 숫자는 4개의 기본 산술 연산과 제곱근의 추출을 사용하여 작성할 수 있지만 고차 뿌리가 없는 경우에만 구성할 수 있다.
직선 및 컴퍼스 공구
직선자와 나침반 구조의 "직선"과 "공감"은 현실 세계에서 지배자와 나침반의 이상화다.
- 직선 가장자리는 무한히 길지만 그 위에 표시가 없고 일반 통치자와는 달리 직선 가장자리 하나만 있다. 그어진 선은 무한히 얇은 점 너비다. 두 점 사이에 선분할을 그리는 데만 사용할 수 있으며, 그 점들에 대해 무한정 정밀도를 유지하거나, 기존 세그먼트를 확장하는 데만 사용할 수 있다.
- 나침반은 임의로 넓게 열 수 있지만 (일부 실제 나침반과는 달리) 그 위에 표시가 없다. 원은 두 개의 주어진 점, 즉 원의 중심과 점으로부터 시작하여 무한한 정밀도로 그 점들에 맞춰 정렬될 수 있다. 그려지는 호는 무한히 얇은 점 폭이다. 나침반은 원을 그리고 있지 않을 때 무너질 수도 있고 무너지지 않을 수도 있다.
실제 나침반은 무너지지 않고 현대의 기하학적 구조는 종종 이 특징을 사용한다. '충돌 나침반'은 힘이 덜 드는 악기로 보일 것이다. 그러나 유클리드 원소 제1권 제2권 발의안 제2호의 나침반 등가 정리로는 무너지는 나침반을 사용해도 힘이 없어지지 않는다. 비록 그 명제가 옳지만, 그 증거는 길고 체크무늬가 있는 역사를 가지고 있다.[2] 어떤 경우든 등가성은 이 특징이 이상적인 나침반의 정의에 규정되지 않은 이유다.
각각의 구조는 정확해야 한다. 그것을 "눈을 뜨고" (본질적으로 구조를 보고 그 정확도를 추측하거나, 자에 대한 측정 단위와 같은 어떤 형태의 측정을 사용)하고 가까이 하는 것은 해결책으로 간주되지 않는다.
각 공사는 반드시 종료되어야 한다. 즉, 한정된 수의 스텝을 가져야 하며, 더 가까운 근사치의 한계가 되어서는 안 된다.
이렇게 말하면, 직선자 구조와 나침반 구조는 심각한 실제적인 문제가 아니라 장애물처럼 보이지만, 이 제한의 목적은 건설이 정확히 맞다는 것을 증명하기 위한 것이다.
역사
고대 그리스 수학자들은 먼저 직선자와 나침반 구조를 시도했고, 그들은 주어진 길이의 합, 차이, 생산물, 비율, 제곱근을 만드는 방법을 발견했다.[3]: p. 1 또한 주어진 각도의 절반, 다른 각도의 2배인 사각형, 주어진 다각형과 동일한 면적을 가진 사각형, 그리고 3, 4, 5개의[3]: p. xi 면(또는 주어진 다각형의[3]: pp. 49–50 2배수를 가진 다각형)을 구성할 수 있다. 그러나 그들은 특정한 경우를 제외하고는 주어진 각도의 3분의 1을 구성하거나, 주어진 원과 같은 면적을 가진 사각형이나, 다른 면의 숫자로 된 정규 다각형을 구성할 수 없었다.[3]: p. xi 또한 그들은 주어진 면이 있는 입방체의 부피의 두 배가 되는 입방체의 옆면을 구성할 수도 없었다.[3]: p. 29
히포크라테스와 메나에흐무스는 하이퍼볼라와 포물선의 교차점을 찾음으로써 큐브의 부피를 배가시킬 수 있다는 것을 보여주었지만, 이것들은 직선자와 나침반으로 구성될 수 없다.[3]: p. 30 기원전 5세기에 히피아스는 4각형이라고 부르는 곡선을 사용하여 일반적인 각도와 원을 모두 삼각형으로 만들었고, 기원전 2세기 니코메데스는 임의의 각도를 삼각형으로 만드는 방법을 보여주었지만,[3]: p. 37 이러한 방법 역시 직선자와 나침반만으로 따를 수는 없다.
미해결된 문제들에 대한 진전은 2천년 동안 이루어지지 않았다. 1796년 가우스는 17개의 면을 가진 일반 다각형이 건설될 수 있다는 것을 보여주었고, 5년 후 그는 n개의 다각형이 건설될 수 있는 충분한 기준을 보여주었다.[3]: pp. 51 ff.
1837년 피에르 원젤은 길이의 큐브 뿌리를 형성하는 것이 불가능하다는 것에 근거하여 임의의 각도를 트리싱하거나 큐브의 볼륨을 두 배로 증가시키는 것이 불가능하다는 증거를 발표했다.[4] 그는 또한 일반 다각형에 대한 가우스의 충분한 시공성 조건 또한 필요하다는 것을 보여주었다.[5]
그 후 1882년 린데만은 이(가) 초월수라는 것을 보여주었고, 따라서 주어진 원과 같은 면적의 사각형을 직선과 나침반으로는 불가능하다는 것을 보여주었다.[3]: p. 47
기본 구성
모든 직선 및 나침반 구조는 이미 구성된 점, 선, 원을 사용하여 5개의 기본 구조를 반복적으로 적용하는 것으로 구성된다. 다음은 다음과 같다.
- 기존 점 두 개를 통해 선 작성
- 한 점을 통과하여 원을 만들고 다른 점을 중앙에 배치
- 두 개의 기존 평행하지 않은 선의 교차점 작성
- 선과 원의 교차점에 하나 또는 두 개의 점 작성( 교차하는 경우)
- 두 원의 교차점에 하나 또는 두 개의 점 작성( 교차하는 경우)
예를 들어, 두 개의 뚜렷한 점으로 시작하는 선이나 두 개의 원 중 하나를 만들 수 있다(회전하여 각 점을 중심으로 사용하고 다른 점을 통과). 두 원을 모두 그리면 교차점에 두 개의 새로운 점이 만들어진다. 두 개의 원래 점과 이 새로운 점들 중 하나 사이에 선을 그리면 정삼각형의 구성이 완료된다.
그러므로 어떤 기하학적 문제에서든 우리는 초기 기호(점수와 선), 알고리즘, 그리고 약간의 결과를 가지고 있다. 이러한 관점에서 기하학은 그 원소를 기호로 대체하여 자명대수에 해당한다. 아마도 가우스는 처음에 이것을 깨닫고, 그것을 몇몇 건축물의 불가능성을 증명하는데 사용했을 것이다; 훨씬 후에야 힐버트는 기하학에 대한 완전한 공리들을 발견했다.
많이 사용되는 직선자 및 나침반 구조
가장 많이 사용되는 직선자 및 나침반 구조물은 다음과 같다.
- 세그먼트에서 수직 이등분선 구성
- 세그먼트의 중간점 찾기
- 점에서 선으로 수직선을 그린다.
- 양분각
- 선에서 점 미러링
- 원에 접하는 점을 통한 선 구성
- 3개의 비협착점을 통한 원 구성
- 주어진 점과 평행하게 선을 그린다.
구성 가능한 점 및 길이
| 대수적 연산에 해당하는 직선 및 나침반 구조 | ||
|---|---|---|
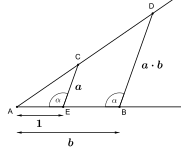
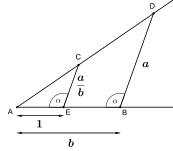
구성될 수 있는 것의 많은 부분은 탈레스의 절편 정리에서 다루어진다.
우리는 두 개의 선으로 이루어진 데카르트 좌표계를 사용하여 대수학을 기하학과 연관시킬 수 있고 벡터로 평면의 점을 나타낼 수 있다. 마지막으로 우리는 이 벡터를 복잡한 숫자로 쓸 수 있다.
선과 원에 대한 방정식을 사용하면 그들이 교차하는 점이 선의 두 점, 원의 중심, 원의 반지름을 포함하는 가장 작은 필드 F의 2차 확장에 있음을 알 수 있다. 즉, x, y, k가 F인 x +y√k 형식이다.
생성 가능한 점의 장은 제곱근으로 닫혀 있기 때문에, 합리적인 계수를 갖는 복잡한 수 영역의 2차 확장의 유한한 순서에 의해 얻을 수 있는 모든 점을 포함하고 있다. 위의 단락에 의해, 어떤 구성 가능한 지점은 그러한 연장의 순서에 의해 얻을 수 있다는 것을 보여줄 수 있다. 이에 대한 예측으로서, 구성 가능한 점(따라서 구성 가능한 길이)에 대한 최소 다항식의 정도가 2의 검정력임을 알게 된다. 특히 모든 대수적 숫자가 구성 가능한 것은 아니지만, 모든 구성 가능한 점(또는 길이)은 대수적 숫자다. 예를 들어, 22는 대수학이지만 구성 가능한 것은 아니다.[4]
구성 가능한 각도
구성 가능한 각도와 구성 가능한 원 위에 구성 가능한 점 사이에 편차가 있다. 추가 modulo 2π(복잡한 숫자로 간주되는 단위 원의 점의 곱셈에 해당한다)에 따라 구성 가능한 각도가 아벨리아 그룹을 형성한다. 구성 가능한 각도는 접선(또는 동등하게, 사인 또는 코사인)이 숫자로 구성 가능한 각도를 정확히 말한다. 예를 들어, 정규 헵타데카곤 (17면 일반 다각형)은 다음과 같은 이유로 구성 가능하다.
생성 가능한 각도의 그룹은 (복잡한 숫자에 제곱근을 갖는 것에 해당하는) 반각의 작업 하에서 폐쇄된다. 두 점으로 시작하는 유한한 순서의 유일한 각도는 순서가 2의 힘 또는 2의 힘과 구별되는 페르마 프리임의 산물인 각이다. 게다가 무한질서의 구성 가능한 각도가 촘촘히 쌓여 있다.
복잡한 산술로서의 직선 및 컴퍼스 구성
유클리드 평면에서 점 집합이 주어지는 경우, 임의의 방향 선택과 함께 그 중 하나를 0으로 부르고 다른 하나를 1로 선택하면 복잡한 숫자의 집합으로 간주할 수 있다.
그러한 점 집합을 복잡한 숫자로 해석할 때, 유효 직선자와 나침반 구성만을 사용하여 구성할 수 있는 점들은 정확히 원래 점 집합을 포함하고 복잡한 결합과 제곱근 연산에 따라 닫히는 최소 영역의 요소들이다(불확실성을 피하기 위해, 우리는 제곱을 지정할 수 있다). π)보다 작은 복잡한 논법으로 뿌리를 내리다. 이 분야의 원소는 정확히 추가, 뺄셈, 곱셈, 나누기, 복합결합, 제곱근의 연산만을 사용하여 원래 포인트의 공식으로 표현할 수 있는 요소들로, 평면의 계산 가능한 밀집된 부분집합으로 쉽게 볼 수 있다. 이 여섯 가지 작업은 각각 단순한 직선자 구조와 나침반 구조에 해당한다. 그러한 공식으로부터 각 산술 연산에 대한 구문을 조합하여 해당 점의 구문을 생산하는 것이 간단하다. 특정 점 집합의 보다 효율적인 구성은 그러한 계산에서 바로 가기에 해당한다.
동등하게(그리고 임의로 두 점을 선택할 필요는 없음) 우리는 임의의 방향 선택에 따라 점 집합이 어떤 두 쌍의 점 사이의 차이 비율에 의해 주어진 일련의 복잡한 비율을 결정한다고 말할 수 있다. 그러한 비율의 집합에서 직선자와 나침반을 사용하여 구성할 수 있는 비율 집합은 원래 비율을 포함하는 가장 작은 영역이며 복잡한 접합자와 제곱근을 사용하여 닫힌다.
예를 들어, 점 또는 비율 z의 실제 부분, 가상 부분 및 계수(위의 두 가지 관점 중 하나를 취함)는 다음과 같이 표현될 수 있으므로 구성 가능하다.
각도의 입방체 및 삼분법을 두 배로 하는 것(예를 들어 special/2π는 분모가 3으로 분할되지 않는 합리적인 숫자인 φ과 같은 특별한 각도는 제외)은 입방정식에 대한 해결책인 비율을 요구하는 반면 원을 제곱하려면 초월비가 필요하다. 이들 중 어느 것도 기술된 분야에 있지 않기 때문에 이들을 위한 직선자와 나침반 구조는 존재하지 않는다.
불가능한 구성
고대 그리스인들은 그들이 풀 수 없는 건축 문제는 해결이 불가능한 것이 아니라 단순히 완고하다고 생각했다.[7] 그러나 현대적인 방법으로는 이러한 직선화와 나침반구조는 논리적으로 수행이 불가능한 것으로 나타났다.(그러나 문제 자체는 해결이 가능하며, 그리스인들은 직선자와 나침반으로만 작업하는 제약 없이 해결할 수 있는 방법을 알고 있었다.)
원을 스퀴딩
원의 사분오열이라고도 알려진 원을 제곱하는 이러한 문제들 중 가장 유명한 것은 직선자와 나침반만을 사용하여 주어진 원과 동일한 면적의 사각형을 건설하는 것이다.
원을 제곱하는 것은 초월수, 즉 transcendπ을 생성하는 것을 포함하기 때문에 불가능하다는 것이 입증되었다. 오직 특정한 대수적 숫자만이 자와 나침반만으로 구성될 수 있는데, 즉 덧셈, 뺄셈, 곱셈, 나누기, 제곱근의 연산 순서가 유한한 정수로 구성된다. 이런 이유로 원을 스퀴딩(squareing the circle)이라는 말이 '불가능한 일을 한다'는 뜻으로 쓰이는 경우가 많다.
자와 나침반만으로 해결책을 요구하는 제약이 없다면, 그 문제는 다양한 기하학적, 대수적 수단에 의해 쉽게 해결될 수 있으며, 고대에 여러 번 해결되었다.[8]
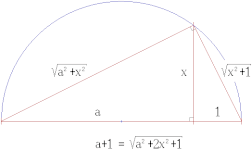
케플러 삼각형을 사용하여 "원의 수"에 근접한 방법을 얻을 수 있다.
큐브 더블링
큐브를 두 배로 늘린다는 것은 주어진 에지를 가진 큐브보다 두 배의 부피를 가진 큐브 가장자리의 직선 가장자리와 나침반만을 사용하는 구조다. 2의 세제곱근은 대수학이지만 덧셈, 뺄셈, 곱셈, 나누기, 제곱근을 취함으로써 정수로 계산할 수 없기 때문에 이것은 불가능하다. 이것은 이성들에 대한 그것의 최소 다항식이 3도를 가지고 있기 때문에 뒤따른다. 이 건축은 두 개의 표시가 있는 직선 가장자리와 나침반을 이용하여 가능하다.
각도 삼분법
각도 삼분법이란 주어진 임의 각도의 3분의 1인 각도의 직선과 나침반만 사용하는 구조를 말한다. 이것은 일반적인 경우에 불가능하다. 예를 들어 각도 2㎛/5라디안(72° = 360°/5)은 검출할 수 있지만 ㎥/3라디안(60°)은 검출할 수 없다.[9] 일반적인 삼분법 문제도 2개의 표시가 있는 직선자(네우스식 건축)가 허용될 때 쉽게 해결된다.
타원까지의 거리
평면의 어느 지점에서 원 위의 가장 가까운 지점까지의 선 세그먼트는 구성할 수 있지만, 평면의 어느 지점에서 양의 편심 타원상의 가장 가까운 지점까지의 세그먼트는 일반적으로 구성할 수 없다.[10]
알하젠 문제
1997년 옥스퍼드 수학자 피터 M. 노이만은 고대 알하센 문제의 일반적인 해결책(구형 거울에서 나온 빌리어 문제 또는 반사)에 대한 지배자와 우위적 구조가 없다는 정리를 증명했다.[11][12]
일반 다각형 구성

일부 일반 다각형(예: 펜타곤)은 직선자와 나침반으로 구성하기 쉽고, 다른 다각형은 그렇지 않다. 이로 인해 다음과 같은 의문이 생겼다. 가장자리와 나침반을 가진 모든 일반 다각형을 만드는 것이 가능한가?
1796년 칼 프리드리히 가우스(Carl Friedrich Gauss)는 규칙적인 17면 다각형이 구성될 수 있다는 것을 보여주었고, 5년 후 n의 기묘한 주요 요인이 구별되는 페르마 프라임이라면 규칙적인 n면 다각형이 직선자와 나침반으로 구성될 수 있다는 것을 보여주었다. 가우스는 이 조건도 필요하다고 추측했지만, 1837년 피에르 원젤이 제공한 이 사실의 증거를 제시하지 않았다.[5]
처음 몇 개의 구성 가능한 일반 다각형은 다음과 같은 면 수를 가진다.
- 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30, 32, 34, 40, 48, 51, 60, 64, 68, 80, 85, 96, 102, 120, 128, 136, 160, 170, 192, 204, 240, 255, 256, 257, 272... (OEIS에서 시퀀스 A003401)
면수가 짝수인 시공 가능한 일반 폴리곤(일반 n곤이 시공 가능한 경우, 일반 2n곤이 시공 가능하여 4n곤, 8n곤 등이 시공 불가능한 것으로 알려져 있다). 그러나 면 수가 홀수인 것으로 알려진 구성 가능한 정규 n-gon은 31개뿐입니다.
세 개의 주어진 특성 점 또는 길이로 삼각형 구성
삼각형의 16개의 요점은 정점, 옆면의 중간점, 고도의 발, 내부 각 이등분자의 발, 그리고 그것의 원곡선, 중심, 직각점, 그리고 유인물이다. 이것들은 한번에 3개를 취해서 3개의 지점에서 삼각형을 구성하는 139개의 뚜렷한 비종교적인 문제들을 산출할 수 있다.[13] 이러한 문제 중 3개는 다른 두 지점으로부터 독특하게 구성될 수 있는 지점을 포함한다; 23은 비독점적으로 구성될 수 있지만(사실상 많은 해결책의 경우), 지점의 위치가 특정 제약조건을 따르는 경우에만 구성될 수 있다; 74의 문제는 일반적인 경우 구성 가능하다; 39의 경우 요구되는 삼각형이 존재하지만 존재하지 않는다.구성 가능한
삼각형의 12개의 키 길이는 3개의 측면 길이, 3개의 고도, 3개의 중위수, 3개의 각 이등분선이다. 이들 각도는 세 각도와 함께 95개의 구별되는 조합을 제공하며, 이 중 63개는 구성 가능한 삼각형을 발생시키고, 30개는 구성되지 않으며, 2개는 정의되지 않는다.[14]: pp. 201–203
제한된 구성
나침반과 직선자가 할 수 있는 모든 것을 여전히 건설할 수 있는 최소 기준을 결정하기 위해서 뿐만 아니라, 무엇이 여전히 건설 가능한지 그리고 그것이 어떻게 건설될 수 있는지를 결정하기 위해서, 다양한 규칙에 따라 건축에 허용되는 도구를 제한하기 위한 다양한 시도가 이루어졌다.
눈금자 또는 나침반만 사용하여 구성
주어진 데이터와 찾을 데이터가 분리된 점(선이나 원이 아닌)으로 이루어진다면 (모어-마스케로니 정리에 따라) 단지 나침반만으로 어떤 것이든 구성할 수 있다. 이 정리의 진실은 아르키메데스의 공리의 진실에 달려 있는데,[15] 이것은 자연에서 일차적인 것이 아니다.
자만으로는 제곱근을 취할 수 없기 때문에 자로 구성할 수 없는 것도 나침반으로 만들 수 있지만, (퐁셀레-스티너 정리) 하나의 원과 그 중심이 주어지면 만들 수 있다.
확장 시공
고대 그리스인들은 그들의 해결책에 필요한 도구들의 복잡성에 따라 건축물을 세 가지 주요 범주로 분류했다. 어떤 건설이 직선 가장자리와 나침반만을 사용하는 경우에는 평면이라고 불렀고, 하나 이상의 원뿔 부분(원 제외)을 필요로 한다면 고체라고 불렀다. 세 번째 범주는 다른 두 범주 중 어느 한 범주에도 속하지 않는 모든 건설을 포함했다.[16] 이 분류는 현대의 대수학적 관점과 잘 어울린다. (위에서 설명한 바와 같이) 현장 운영과 제곱근만을 사용하여 표현할 수 있는 복잡한 숫자에 평면구성이 있다. 큐브 뿌리의 추출도 포함하는 복잡한 숫자는 견고한 구조를 가지고 있다.
필드의 언어에서 평면인 복잡한 숫자는 2의 힘을 가지며, 각 연장이 2도를 갖는 필드의 탑으로 분해될 수 있는 필드 연장에 놓여 있다. 시공성이 탄탄한 단지수는 2, 3분의 1인자로 학위가 있고, 각 연장이 2, 3도인 밭탑 꼭대기에 있는 밭연장에 놓여 있다.
솔리드 구성
점은 이미 구성된 초점, 다이렉트릭스, 편심률로 원뿔을 그릴 수 있는 직선 에지, 나침반, 원뿔 그리기 도구를 사용하여 구성할 수 있다면 견고한 구조를 가지고 있다. 동일한 점 집합은 종종 더 작은 도구 집합을 사용하여 구성할 수 있다. 예를 들어, 포물선 y=x를2 포인트(0,0), (1,0)와 함께 가지고 있는 나침반, 직선자, 종이를 사용하면 견고한 구조를 가진 어떤 복잡한 숫자도 만들 수 있다. 마찬가지로 이미 구성된 초점과 주요 축(두 개의 핀과 한 개의 끈을 생각)으로 어떤 타원을 그릴 수 있는 도구는 그만큼 강력하다.[17]
고대 그리스인들은 입방체를 두 배로 하는 것과 임의의 각도를 세로로 감지하는 것 둘 다 견고한 구조를 가지고 있다는 것을 알았다. 아르키메데스는 정규 7곤을 탄탄하게 시공했다. 원의 4각형은 견고한 구조를 가지고 있지 않다.
일반 n곤은 pierpont primes가 구별되는jk pierpont primes(양식rs 23+1의 primes) 제품인 경우에만 견고한 구조를 가지고 있다. 그러한 n의 집합은 순서다.
- 7, 9, 13, 14, 18, 19, 21, 26, 27, 28, 35, 36, 37, 38, 39, 42, 45, 52, 54, 56, 57, 63, 65, 70, 72, 73, 74, 76, 78, 81, 84, 90, 91, 95, 97... (OEIS에서 A051913 시퀀스)
일반 n곤이 견고한 구조를 가지지 않는 n의 집합은 순서다.
- 11, 22, 23, 25, 29, 31, 33, 41, 43, 44, 46, 47, 49, 50, 53, 55, 58, 59, 61, 62, 66, 67, 69, 71, 75, 77, 79, 82, 83, 86, 87, 88, 89, 92, 93, 94, 98, 99, 100... (OEIS에서 시퀀스 A048136)
페르마 프라임즈와의 질문처럼 피에르폰트 프라임이 무한히 많은가에 대한 공개적인 질문이다.
각도 삼분법
직선자와 나침반과 함께 임의의 각도를 감지할 수 있는 도구가 있다면 어떨까? 이러한 구조는 견고한 구조지만, 그러한 도구를 사용하여 구성할 수 없는 견고한 구조를 가진 숫자들이 존재한다. 예를 들어, 우리는 그런 도구로는 큐브를 두 배로 늘릴 수 없다.[18] 한편, 견고한 구조를 가진 모든 일반 n곤은 그러한 도구를 사용하여 구성할 수 있다.
종이접기
종이접기의 수학적 이론은 직선자와 나침반 구조보다 더 강력하다. Huzita-Hateri 공리를 만족하는 접기는 나침반과 원뿔 그리기 도구를 사용하여 확장된 구조와 정확히 동일한 점 집합을 구성할 수 있다. 따라서 종이접기는 입방정식(따라서 사분방정식)을 푸는 데도 사용될 수 있으며, 따라서 고전적인 문제 중 두 가지를 해결할 수 있다.[19]
표시 가능한 통치자
아르키메데스, 니코메데스, 아폴로니우스는 주목할 만한 통치자의 사용과 관련된 공사를 했다. 이를 통해 선분할, 선(또는 원) 두 개 및 점을 취할 수 있으며, 그런 다음 주어진 점을 통과하여 두 선을 교차하는 선을 그려 교차점 사이의 거리가 주어진 세그먼트와 같도록 할 수 있다. 이것은 그리스인들이 네우시스("침입", "긴장" 또는 "검열")라고 불렀는데, 그 이유는 새로운 선들이 요점을 찌르기 때문이다. 이 확장된 계획에서 우리는 임의의 각도를 추적하거나(아키메데스의 삼분법 참조) 임의의 큐브 루트를 추출할 수 있다(니코메데스로 인한). 따라서 기존 거리 대비 비율이 입방정식 또는 4분위 방정식의 해법인 모든 거리는 구성 가능하다. 표시 가능한 자를 사용하면 헵타곤과 같이 견고한 구조를 가진 일반 다각형이 구성되며, 존 H. 콘웨이와 리차드 K도 구성 가능하다. 그 중 [20]몇 개는 건축을 맡았지
네우시스 구조는 원뿔형 그리기 도구보다 더 강력한데, 견고한 구조물이 없는 복잡한 숫자를 만들 수 있기 때문이다. 사실, 이 도구를 사용하면 급진기를 사용하여 해결할 수 없는 일부 5중주를 해결할 수 있다.[21] 원시도가 7보다 크거나 같은 수정불가능한 다항식은 네우스시 공법을 사용하여 해결할 수 없는 것으로 알려져 있어 이 공구를 사용하여 일반 23곤이나 29곤을 시공할 수 없다. 벤자민과 스나이더는 정규 11곤 건설이 가능하다는 것을 증명했지만, 시공을 하지 않았다.[22] 이 도구를 사용하여 일반 25곤 또는 31곤을 구성할 수 있는지 여부에 대해서는 여전히 개방되어 있다.
이진수 계산
1998년 사이먼 플로프는 특정 숫자의 이진수를 계산하는 데 사용할 수 있는 자와 나침반 알고리즘을 제공했다.[23] 알고리즘은 각도를 반복적으로 두 배로 증가시키는 것을 포함하며 약 20개의 이진수 이후 물리적으로 비실용적이 된다.
참고 항목
- 칼라일 서클
- 기하학 암호학
- 기하그래피
- 대화형 지오메트리 소프트웨어 목록, 대부분 직선자와 나침반 구조를 보여준다.
- 종이접기의 수학
- 잘못된 직선자와 나침반 증거를 수집하는 부업으로 삼은 수학자 언더우드 더들리.
참조
- ^ Underwood Dudley (1983), "What To Do When the Trisector Comes" (PDF), The Mathematical Intelligencer, 5 (1): 20–25, doi:10.1007/bf03023502
- ^ 고드프리드 뚜생 "유클리드의 두 번째 명제에 대한 새로운 시선," 수학 지능 지수 15권, 3권, (1993), 페이지 12-24.
- ^ a b c d e f g h i 대담해, 벤자민 기하학의 유명한 문제들과 그것들을 해결하는 방법, 도버 출판물들, 1982년 (기원. 1969년)
- ^ a b Wantzel, Pierre-Laurent (1837). "Recherches sur les moyens de reconnaître si un problème de Géométrie peut se résoudre avec la règle et le compas" (PDF). Journal de Mathématiques Pures et Appliquées. 1. 2: 366–372. Retrieved 3 March 2014.
- ^ a b Kazarinoff, Nicholas D. (2003) [1970]. Ruler and the Round. Mineola, N.Y.: Dover. pp. 29–30. ISBN 978-0-486-42515-3.
- ^ Weisstein, Eric W. "Trigonometry Angles--Pi/17". MathWorld.
- ^ Stewart, Ian. Galois Theory. p. 75.
- ^ *MacTutor에서 원 스쿼싱
- ^ 72인치 각도를 감지하는 방법.
- ^ 아자드, H, 라라지, A, "초기 기하학에서 불가능한 건축", 2004년 11월, 수학적 가제트 88, 548–551.
- ^ Neumann, Peter M. (1998), "Reflections on Reflection in a Spherical Mirror", American Mathematical Monthly, 105 (6): 523–528, doi:10.1080/00029890.1998.12004920, JSTOR 2589403, MR 1626185
- ^ Highfield, Roger (1 April 1997), "Don solves the last puzzle left by ancient Greeks", Electronic Telegraph, 676, archived from the original on November 23, 2004, retrieved 2008-09-24
- ^ 파스칼 슈렉, 파스칼 마티스, 베스나 마린코비, 프레드랙 야니치. "Wernick's list: a final update", Forum 기하학orum 16, 2016, 페이지 69–80. http://forumgeom.fau.edu/FG2016volume16/FG201610.pdf
- ^ 포사멘티어, 알프레드 S, 레만, 잉그마르. 프로메테우스 북스, 2012년 삼각형의 비밀
- ^ Avron, Arnon (1990). "On strict strong constructibility with a compass alone". Journal of Geometry. 38 (1–2): 12–15. doi:10.1007/BF01222890.
- ^ T.L. 히스 "그리스 수학의 역사, 제1권"
- ^ P. 험멜, "타원을 이용한 견고한 건축", "파이 무 엡실론 저널", 11(8), 429 -- 435 (2003)
- ^ Gleason, Andrew: "각도 삼분해, 헵타곤, 그리고 삼분해," Amer. 수학. 월 95 (1988), 3번, 185-194.
- ^ Row, T. Sundara (1966). Geometric Exercises in Paper Folding. New York: Dover.
- ^ 콘웨이, 존 H. 그리고 리차드 가이: The Book of Numbers
- ^ A. 바라가르, "Tweeps-Notched Straighted edge를 사용한 건설", "The American Mathemical Monthly", 109(2), 151 - 164(2002년).
- ^ E. 벤자민, C. 스나이더(Snyder), "표기된 통치자와 나침반에 의한 정규 헨데카곤의 건설에 대하여," 케임브리지 철학회의 수학 프로시저 156(3), 409 - 424(2014).
- ^ Simon Plouffe (1998). "The Computation of Certain Numbers Using a Ruler and Compass". Journal of Integer Sequences. 1. ISSN 1530-7638.
외부 링크
- 수학 포럼에서 수학 박사에 의한 규칙적인 다각형 건축 @ 드렉셀
- 나침반을 사용한 건설 단지 코튼마우트에서만 가능
- 히포크라테스의 앵글 트리세션(Angle Triseation)을 즉시 사용
- Weisstein, Eric W. "Angle Trisection". MathWorld.


 (가)
(가)