복합 기하학

수학에서 복잡한 기하학은 복잡한 숫자로 인해 발생하거나 또는 기술하는 기하학적 구조와 구조에 대한 학문이다. 특히 복합기하학은 복합다지관과 복합대수종과 같은 공간, 여러 복합변수의 함수, 홀로모르픽 벡터다발과 일관성 있는 절편과 같은 홀로모르프 구성의 연구와 관련이 있다. 대수 기하학에 대한 초월적 방법의 적용은 복잡한 분석의 기하학적 측면과 함께 이 범주에 포함된다.

복잡한 기하학은 대수 기하학, 미분 기하학, 복잡한 분석의 교차점에 위치하며, 세 영역 모두에서 도구를 사용한다. 다양한 영역의 기법과 사상이 혼합되어 있기 때문에 복잡한 기하학의 문제들은 일반적으로 보다 다루기 쉬우거나 구체적이다. 예를 들어, 최소 모델 프로그램을 통한 복합 다지관과 복합 대수 변종 분류와 모듈리 공간의 구성은 가능한 매끄러운 다지관의 분류가 현저하게 어려운 문제인 미분 기하학과는 분야를 구분한다. 또한, 복잡한 기하학의 추가적인 구조는 특히 콤팩트한 환경에서, 칼라비 추측에 대한 신퉁 야우의 증명, 히친-코바야시 통신, 비아벨리안 호지 통신, 케흘러-아인슈타인 지표와 콘의 존재 결과 등, 세계적인 분석 결과를 크게 입증하는 것을 가능하게 한다.스칼라 곡률 Kahler 측정 기준.

복잡한 기하학은 이론 물리학에 중요한 응용을 가지고 있는데, 여기서 그것은 일치장 이론, 끈 이론, 거울 대칭을 이해하는 데 필수적이다. 그것은 종종 보렐-윌-보트 정리로 이어지는 복잡한 기하학을 이용하여 일반화된 국기 품종을 연구할 수 있는 표현 이론이나, 복잡한 다지관이 이국적인 예시를 제공하는 리만 기하학에서 케흘러 다지관이 공통적인 공통적 기하학에서 연구될 수 있는 표현 이론을 포함한 수학의 다른 영역에서 예시의 원천이 되는 경우가 많다. 칼라비-와 같은 미터법 구조Yau 다지관과 하이퍼켈러 다지관, 그리고 게이지 이론에서 홀로모픽 벡터 번들은 종종 양-밀스 방정식과 같은 물리학에서 발생하는 중요한 미분 방정식에 대한 해결책을 인정한다. 복합 기하학은 순수 대수 기하학에서 추가적으로 영향을 미치는데, 여기서 케흘러 다지관의 호지 이론과 같은 복잡한 설정의 분석 결과는 p-adic Hodge 이론뿐만 아니라 다양성과 계획들에 대한 호지 구조에 대한 이해를 고취시키고, 복합 다지관의 변형 이론은 변형 이론에 대한 이해를 고취시킨다 o.복잡한 다지관의 동족학에 대한 f 계획과 결과는 Weil 추측과 그로텐디크의 표준 추측의 형성에 영감을 주었다. 한편, 이러한 많은 분야에서 얻은 결과와 기술은 종종 복잡한 기하학으로 되돌아온다. 예를 들어 끈 이론과 거울 대칭의 수학의 발전은 칼라비–의 본질에 대해 많은 것을 밝혀냈다.끈 이론가들이 예측하는 야우 다지관은 SYZ 억측을 통해 라그랑지안 섬유 구조를 가져야 하며 , 그로모프-위튼의 동조 다지관 이론의 발달로 복잡한 품종의 열거적 기하학이 발전하게 되었다.

밀레니엄 상금 문제 중 하나인 호지 추측이 복잡한 기하학에서 문제가 되고 있다.^[1]

아이디어

복잡한 공간의 대표적인 예가 복잡한 투영 선이다. 그것은 구, 즉 미분 기하학에서 발생하는 매끄러운 다지관 또는 무한대에 점을 추가하여 복잡한 평면의 연장인 리만 구로 볼 수 있다.

대체로 복잡한 기하학은 어떤 의미에서 복잡한 평면에서 모델링된 공간과 기하학적 물체와 관련이 있다. 단일 변수에 대한 복잡한 평면 및 복잡한 분석의 특징, 예를 들어 내적인 방향성 개념(즉, 복잡한 평면의 모든 지점에서 시계 반대 방향으로 90도 일관되게 회전할 수 있음) 및 홀로모르픽 함수(즉, 단일 복합 파생상품의 존재는 복잡한 차이점을 내포함)의 경직성.모든 주문에 대한 tiability)는 복잡한 기하학 연구의 모든 형태에서 나타나는 것으로 보인다. 예를 들면, 모든 복합다지관은 성론적으로 방향을 잡을 수 있으며, 리우빌의 정리의 형태는 콤팩트 복합다지관이나 투영 복합대수학 변종에 관한 것이다.

복잡한 기하학은 실제 기하학이라고 불릴 수 있는 것과 향미가 다르다. 즉, 실제 숫자 선의 기하학적 특성 및 해석적 특성을 중심으로 한 공간에 대한 연구. 예를 들어, 매끄러운 다지관은 개방된 집합에 있는 것과 동일할 수 있는 매끄러운 기능의 집합, 그리고 다른 곳에서도 똑같이 0인 단결성의 파티션을 허용하는 반면에, 복잡한 다지관은 그러한 홀모픽 함수의 집합은 인정하지 않는다. 실제로 이것은 단일 변수에 대한 복잡한 분석의 전형적 결과인 정체성 정리의 발현이다. 어떤 의미에서 복잡한 기하학의 신기함은 이러한 근본적인 관찰로 거슬러 올라갈 수도 있다.

모든 복잡한 다지관은 특히 정말 매끄러운 다지관인 것은 사실이다. 복합 평면 $\mathbb {C}$ ${\$ 은 $\mathbb {C}$ (는) 복잡한 구조를 잊어버린 후 실제 평면 R $\mathbb {R} ^{2}$ ${\$ 그러나 복잡한 기하학은 일반적으로 부드러운 다지관의 연구인 미분 기하학의 특정 하위 영역으로 보지 않기 때문이다 $\mathbb {R} ^{2}$ 특히 Serre의 GAGA 정리는 모든 투사적 분석적 다양성이 실제로 대수적 다양성이며, 분석적 다양성에 대한 홀로모르픽 데이터 연구는 대수적 데이터의 연구와 동등하다고 말한다.

이 등가성은 복잡한 기하학이 어떤 의미에서는 미분 기하학보다 대수 기하학에 더 가깝다는 것을 나타낸다. 복잡한 평면의 특성과 다시 연결되는 또 다른 예는 단일 변수의 복잡한 분석에서 용적함수의 특이점은 쉽게 설명할 수 있다는 것이다. 대조적으로, 연속적인 실질 가치 함수의 가능한 단수적 행동은 특성화하기 훨씬 더 어렵다. 그 결과, 단수 복합 분석 품종이나 단수 복합 대수 품종과 같은 복잡한 기하학에서 단수적인 공간을 쉽게 연구할 수 있는 반면, 미분 기하학에서는 단수적인 공간에 대한 연구는 피하게 되는 경우가 많다.

실제로 복잡한 기하학은 여러 가지 복잡한 변수에서 미분 기하학, 대수 기하학, 분석의 교차점에 위치하며, 복잡한 지오미터는 세 분야 모두에서 도구를 사용하여 복잡한 공간을 연구한다. 복잡한 기하학에 대한 전형적인 관심 방향은 복잡한 공간의 분류, 그것들에 부착된 홀로모르픽 물체들에 대한 연구(홀로모르픽 벡터 번들 및 일관성 있는 깎기 등), 그리고 복잡한 기하학적 물체와 수학 및 물리학의 다른 영역들 사이의 친밀한 관계를 포함한다.

정의들

복잡한 기하학은 복잡한 다지관, 그리고 복잡한 대수학 및 복잡한 분석 변종들의 연구와 관련이 있다. 이 절에서는 이러한 유형의 공간을 정의하고 공간 간의 관계를 제시한다.

복합 다지관은 위상학적 공간 $X$ $X$ 이며, 다음과 $X$ 같다.

$X$ $X$ 은(는) 하우스도르프(Hausdorff)이며 $X$ 두 번째 카운트할 수 있다.
$X$ is locally homeomorphic to an open subset of $\mathbb {C} ^{n}$ for some $n$ . That is, for every point $p\in X$ , there is an open neighbourhood $U$ of $p$ and a homeomorphism $\varphi :U\to V$ ${\displaystyle \varphi :$ $U\to V}$ 을 $\varphi :U\to V$ (를) 열린 부분 집합 $V\subseteq \mathbb {C} ^{n}$ $V\subseteq \mathbb {C} ^{n}$ $V\subseteq \mathbb {C} ^{n}$ $V\subseteq \mathbb {C} ^{n}$ ${\$ 에 $V\subseteq \mathbb {C} ^{n}$ 이러한 열린 집합을 차트라고 한다.
If $(U_{1},\varphi )$ and $(U_{2},\psi )$ are any two overlapping charts which map onto open sets $V_{1},V_{2}$ of $\mathbb {C} ^{n}$ respectively, then the transition function $\psi \circ \varphi ^{-1}:\varphi (U_{1}\cap U_{2})\to \psi (U_{1}\cap U_{2})$ $\psi \circ \varphi ^{-1}:\varphi (U_{1}\cap U_{2})\to \psi (U_{1}\cap U_{2})$ $\psi \circ \varphi ^{-1}:\varphi (U_{1}\cap U_{2})\to \psi (U_{1}\cap U_{2})$ $∩$ $\psi \circ \varphi ^{-1}:\varphi (U_{1}\cap U_{2})\to \psi (U_{1}\cap U_{2})$ 2 $\psi \circ \varphi ^{-1}:\varphi (U_{1}\cap U_{2})\to \psi (U_{1}\cap U_{2})$ ) $\psi \circ \varphi ^{-1}:\varphi (U_{1}\cap U_{2})\to \psi (U_{1}\cap U_{2})$ → $\psi \circ \varphi ^{-1}:\varphi (U_{1}\cap U_{2})\to \psi (U_{1}\cap U_{2})$ $\psi \circ \varphi ^{-1}:\varphi (U_{1}\cap U_{2})\to \psi (U_{1}\cap U_{2})$ 1 $\psi \circ \varphi ^{-1}:\varphi (U_{1}\cap U_{2})\to \psi (U_{1}\cap U_{2})$ $\psi \circ \varphi ^{-1}:\varphi (U_{1}\cap U_{2})\to \psi (U_{1}\cap U_{2})$ $\psi \circ \varphi ^{-1}:\varphi (U_{1}\cap U_{2})\to \psi (U_{1}\cap U_{2})$ ) ${\displaystyle \circ \circ$ \circ $\varphi$ ^{- $1}:\varphi(U_{1$ }\ $cap U_{2})\psi로 가는$ 것은 생체모형이다 $\psi \circ \varphi ^{-1}:\varphi (U_{1}\cap U_{2})\to \psi (U_{1}\cap U_{2})$ $.$

유의할 점은 모든 생체모형은 차이점형이고, $\mathbb {C} ^{n}$ ${\$ ^{ $n}}$ 는 $\mathbb {R} ^{2n}$ $\mathbb {R} ^{2n}$ ${\$ 에 대한 실제 벡터 공간으로서의 이형성이므로 $\mathbb {C} ^{n}$ $\mathbb {R} ^{2n}$ 차원 $n$ ${\displaysty$ $n$ 의 모든 복합 다지형은 특히 차원 $2n$ {n의 부드러운 다지형이 $n$ 된다.언제나 짝수인 $2n$

항상 매끄러운 복잡한 다지관과 대조적으로, 복잡한 기하학 또한 단수적인 공간과 관련이 있다. An affine complex analytic variety is a subset $X\subseteq \mathbb {C} ^{n}$ such that about each point $p\in X$ , there is an open neighbourhood $U$ of $p$ and a collection of finitely many holomorphic functions $f_{1},\dots ,f_{k}:U\to \mathbb {C}$ ${\$ $U\to \mathbb {C} }$ such that $X\cap U=\{z\in U\mid f_{1}(z)=\cdots =f_{k}(z)=0\}=Z(f_{1},\dots ,f_{k})$ . By convention we also require the set $X$ to be irreducible. 점 $p\in X$ $p\in X$ $p\in X$ $p\in X$ 은(는) 홀로모르픽 함수 벡터 $(f_{1},\dots ,f_{k})$ $(f_{1},\dots ,f_{k})$ , $(f_{1},\dots ,f_{k})$ … $(f_{1},\dots ,f_{k})$ , $(f_{1},\dots ,f_{k})$ k $(f_{1},\dots ,f_{k})$ ) ${\displaystyle(f_{1},\dots,f_{k})$ 의 Jacobian 행렬이 $p$ ${\displaystyp$ 에서 전체 순위를 가지지 $(f_{1},\dots ,f_{k})$ 않은 경우 단수가 된다 $p\in X$ . 투사적 복합 분석 다양성은 복합 투사 공간의 $X\subseteq \mathbb {CP} ^{n}$ X $X\subseteq \mathbb {CP} ^{n}$ ⊆ $X\subseteq \mathbb {CP} ^{n}$ $X\subseteq \mathbb {CP} ^{n}$ n ${\$ X $\subseteq \mathb {CP}{n}}$ 이며, 이는 동일한 방식으로 $\mathbb {CP} ^{n}$ $\mathbb {CP} ^{n}$ $\mathbb {CP} ^{n}$ ${\$ 의 오픈 서브셋에 대한 유한 집합 0에 의해 국지적으로 주어진다 $\mathbb {CP} ^{n}$

유사하게 어핀 복합 대수적 다양성을 $부분$ 집합 $X\subseteq \mathbb {C} ^{n}$ $X\subseteq \mathbb {C} ^{n}$ $X\subseteq \mathbb {C} ^{n}$ $X\subseteq \mathbb {C} ^{n}$ ${\$ X $\subseteq \mathb{C} ^n}}$ 로 정의할 수 있으며, 이는 $X\subseteq \mathbb {C} ^{n}$ n ${\displaystyn}$ 복합 $n$ 변수에서 미세하게 많은 다항식의 0 집합으로 로컬로 주어진다. 투영적 복합 대수적 품종을 정의하려면 X $X\subseteq \mathbb {CP} ^{n}$ X $X\subseteq \mathbb {CP} ^{n}$ C $X\subseteq \mathbb {CP} ^{n}$ $X\subseteq \mathbb {CP} ^{n}$ {\ $displaystyle$ X\subseteq $\mathb {CP}$ $^n}$ 이(가) 미세하게 많은 동종 다항식 0 집합에 의해 국소적으로 부여되어야 $X\subseteq \mathbb {CP} ^{n}$ 한다.

일반적인 복잡한 대수학이나 복잡한 분석적 다양성을 정의하기 위해서는 국소적으로 링이 달린 공간의 개념이 필요하다. 복합 대수학/분석적 다양성은 국소적으로 링된 공간 $(X,{\mathcal {O}}_{X})$ , $(X,{\mathcal {O}}_{X})$ ) ${\displaystyle (X,{\mathcal{O}_{X})$ 이며 $(X,{\mathcal {O}}_{X})$ , 국소적으로 아핀 복합 대수학/분석적 다양성에 대한 국소적으로 링된 공간으로서 이형이다. 분석 사례에서는 일반적으로 $X$ ${\displaystyle$ X $}$ 이(가) $\mathbb {C} ^{n}$ ${\$ 의 오픈 하위 집합으로 식별되어 아공간 위상에 국소적으로 동등한 위상(위상 $X$ )을 가질 수 있도록 허용하는 $반면$ 대수 $사례$ 에서는 X {\diski 위상( $위상)$ 이 장착되어 있는 $X$ 경우가 많다 $\mathbb {C} ^{n}$ 다시 한번 말하지만, 관습에 의해 우리는 이 지역적으로 링된 공간이 회복될 수 없도록 요구한다.

단수점의 정의는 국소적이므로, 부속물 분석/알지브라질 다양성에 대해 주어진 정의는 복잡한 분석 또는 대수적 다양성의 점에 적용된다. The set of points of a variety $X$ which are singular is called the singular locus, denoted $X^{sing}$ , and the complement is the non-singular or smooth locus, denoted $X^{nonsing}$ . We say a complex variety is smooth or non-singular if it's singular locus는 비어있다. 즉, 비노래자위치와 동일하다면 말이다.

홀로모르픽 함수에 대한 암묵적 함수 정리에 의해, 모든 복잡한 다지관은 특히 비성적 복합 분석적 다양성이지만, 일반적인 아핀이나 투영적인 것은 아니다. 세레의 GAGA 정리로는 모든 투사적 복합 분석적 다양성이 사실 투사적 복합 대수적 다양성이다. 복잡한 품종이 비성형일 때, 그것은 복잡한 다지관이다. 더 일반적으로, 복잡한 다양성의 비노래적 중심은 복합 다지관이다.

복합공간의 종류

칼러 다지관

복잡한 다지관은 리만 측량법이나 동정적 형태와 같은 추가적인 기하학적 구조를 갖춘 미분 기하학의 관점에서 연구될 수 있다. 이 추가적인 구조가 복잡한 기하학과 관련되기 위해서는 적절한 의미에서 복잡한 구조와 양립할 수 있도록 요청해야 한다. 케흘러 다지관은 리만 메트릭스 및 복합 구조와 호환되는 동조 구조를 가진 복합 다지관이다. Every complex submanifold of a Kähler manifold is Kähler, and so in particular every non-singular affine or projective complex variety is Kähler, after restricting the standard Hermitian metric on $\mathbb {C} ^{n}$ or the Fubini-Study metric on $\mathbb {CP} ^{n}$ respectively.

Kahler 다지관의 다른 중요한 예로는 Riemann 표면, K3 표면, Calabi–이 있다.Yau 다지관.

스타인 다지관

Serre의 GAGA 정리는 투영적인 복합 분석 품종이 실제로 대수학이라고 주장한다. 이것이 붙임성 품종에 대해서는 엄밀히 말하면 사실이 아니지만, 스타인 다지관이라 불리는 붙임성 복합 대수 품종과 매우 흡사하게 작용하는 복합 다지관의 종류가 있다. 다지관 $X$ $X$ 이(가) 홀모형 볼록하고 홀모형으로 분리할 수 있는 경우 스타인이다 $X$ (기술적 정의는 스타인 다지관에 관한 기사 참조). 그러나 이는 일부 $n$ $n$ 에 $\mathbb {C} ^{n}$ $\mathbb {C} ^{n}$ $\mathbb {C} ^{n}$ ${\$ 의 복합 하위 관리형인 $X$ $X$ $X$ 에 해당한다는 것을 알 수 있다 $n$ 스타인 다지관이 복잡한 대수적 변종과 유사한 또 다른 방법은 카르탄의 정리 A와 B가 스타인 것이다.

스타인 다지관의 예로는 비컴팩트 리만 표면과 비싱글 아핀 복합 대수 품종을 들 수 있다.

하이퍼 칼러 다지관

A special class of complex manifolds is hyper-Kähler manifolds, which are Riemannian manifolds admitting three distinct compatible integrable almost complex structures $I,J,K$ which satisfy the quaternionic relations $I^{2}=J^{2}=K^{2$ $=IJK=-\operatorname {Id}$ 따라서 하이퍼 케흘러 다지관은 케흘러 다지관이며, 그 후 풍부한 기하학적 구조를 갖게 된다.

하이퍼 케흘러 다지관의 예로는 ALE 공간, K3 표면, 힉스다발 모듈리 공간, 떨림 품종 및 게이지 이론과 표현 이론에서 발생하는 많은 다른 모듈리 공간이 있다.

칼라비-야우 다양체

5중주 칼라비의 진짜 2차원 조각야우 삼배

언급했듯이, 칼러 다지관의 특정 등급은 칼라비-에 의해 주어진다.Yau 다지관. 이것들은 $K_{X}=\Lambda ^{n}T_{1,0}^{*}X$ 표준 $K_{X}=\Lambda ^{n}T_{1,0}^{*}X$ K X = $K_{X}=\Lambda ^{n}T_{1,0}^{*}X$ $K_{X}=\Lambda ^{n}T_{1,0}^{*}X$ 1 $K_{X}=\Lambda ^{n}T_{1,0}^{*}X$ , $K_{X}=\Lambda ^{n}T_{1,0}^{*}X$ X ${\displaystyle K_{X}=\Lambda^{n}T_{1$ ,0 $}^{*}X}$ 을(를) 가진 Kahler 다지관들에 의해 주어진다 $K_{X}=\Lambda ^{n}T_{1,0}^{*}X$ 일반적으로 칼라비–의 정의.또한 Yau 매니폴드에서는 $X$ {\ $displaystyle X$ }이(가) 소형이어야 한다 $X$ . 이 경우 칼라비 추측에 대한 야우의 증거는 X ${\displaystyle$ X $}$ 이( $가$ ) 리치 곡면성을 소멸시키는 케흘러 메트릭을 인정한다는 $X$ 것을 내포하고 있으며, 이는 칼라비–의 동등한 정의로 받아들여질 수 있다.야우.

칼라비-야우 다지관은 문자열 이론과 거울 대칭에서 사용된다는 것을 발견했는데, 여기서 그것들은 문자열 이론의 10차원 모델에서 여분의 6차원의 스페이스 시간을 모형화하는 데 사용된다. 칼라비-의 예Yau 다지관은 타원 곡선, K3 표면, 복잡한 아벨리아 품종 등에 의해 주어진다.

복합 파노 품종

복합형 파노 품종은 항캐노니컬 라인 번들( $K_{X}^{*}$ $K_{X}^{*}$ $K_{X}^{*}$ ${\$ 이 $K_{X}^{*}$ 풍부한 복합 대수 품종이다. 파노 품종은 복잡한 대수 기하학 기하학, 특히 최소 모델 프로그램에서 종종 발생하는 혼성 기하학에 상당한 관심을 가지고 있다. Fundamental examples of Fano varieties are given by projective space $\mathbb {CP} ^{n}$ where $K={\mathcal {O}}(-n-1)$ , and smooth hypersurfaces of $\mathbb {CP} ^{n}$ of degree less than $n+1$ .

토릭 품종

첫 번째 Hirzebruch 표면을 설명하는 모멘트 폴리토프.

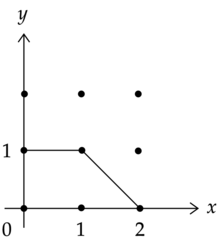
토릭 품종은 $(\mathbb {C} ^{*})^{n}$ ( $(\mathbb {C} ^{*})^{n}$ $(\mathbb {C} ^{*})^{n}$ ) $(\mathbb {C} ^{*})^{n}$ ${\$ 에 대한 개방된 밀도 부분집합 바이홀모픽을 포함하는 $n$ $차원$ n $n$ 의 복합 대수 품종으로 $(\mathbb {C} ^{*})^{n}$ ( $(\mathbb {C} ^{*})^{n}$ $(\mathbb {C} ^{*})^{n}$ ${\mathb$ { $C}{*}}}}{n}}}}}}}}}}$ 의 작용이 확장된다 $(\mathbb {C} ^{*})^{n}$ . 토릭 버라이어티는 그것의 토릭 팬에 의해 결합적으로 묘사될 수 있고, 적어도 그것이 비송음일 때, 순간 폴리토페에 의해 묘사될 수 있다. $\mathbb {R} ^{n}$ 는 $\mathbb {R} ^{n}$ ${\$ 의 폴리곤으로, 모든 정점을 $\operatorname {GL} (n,\mathbb {Z} )$ $\operatorname {GL} (n,\mathbb {Z} )$ ( $\operatorname {GL} (n,\mathbb {Z} )$ , $\operatorname {GL} (n,\mathbb {Z} )$ ) $\operatorname {GL} (n,\mathbb {Z} )$ {\ $displaysty \operatorname {GL}(n,\mathb {Z})$ 의 작용에 의해 양정직 정점의 표준 형태로 넣을 수 있는 속성이 있다 $\mathbb {R} ^{n}$ $\operatorname {GL} (n,\mathbb {Z} )$ 토릭 버라이어티는 폴리토프 위를 기빙하는 적당한 공간으로 얻을 수 있다.

토릭 변종에서 수행되는 많은 구조는 모멘트 폴리토프 또는 관련 토릭 팬의 조합 및 기하학적 측면에서 대체 설명을 허용한다. 이것은 토릭 품종을 복잡한 기하학의 많은 건축물에 특히 매력적인 시험 케이스로 만든다. 토릭 품종의 예로는 복잡한 투영 공간과 그 위에 묶음 등이 있다.

복잡한 기하학의 기법

홀로모픽 함수와 복잡한 다지관의 경직성 때문에, 일반적으로 복합 다지관과 복합 품종을 연구하기 위해 사용되는 기법은 일반 미분 기하학에서 사용되는 기법과는 다르며, 대수 기하학에서 사용되는 기법에 더 가깝다. 예를 들어, 차등 기하학에서는 지역 구조를 취하여 통합의 파티션을 사용하여 전체적으로 패치함으로써 많은 문제에 접근한다. 통합의 칸막이는 복잡한 기하학에서 존재하지 않기 때문에 언제 지역 데이터가 글로벌 데이터에 붙을 수 있는지에 대한 문제는 더욱 미묘하다. 정확히 언제 지역 데이터를 함께 패치할 수 있을지는 피복 코호몰로지(sheaf cohomology)에 의해 측정되며 피복과 피복 그룹의 코호몰로지(cohomology) 집단이 주요 도구다.

예를 들어, 현대적 정의의 도입에 앞서 몇 가지 복잡한 변수들의 분석에서 유명한 문제들은 사촌 문제인데, 글로벌한 용적함수를 얻기 위해 국소적 용적 데이터를 언제 접착할 수 있는지 정확히 물어본다. 이러한 오래된 문제들은 피복과 코호몰로지 집단의 도입 후에 간단히 해결될 수 있다.

복합 기하학에서 사용되는 이음매의 특별한 예로는 홀로모르프 선다발(및 이음매와 연관된 이음매), 홀로모르프 벡터다발, 일관성 있는 이음매 등이 있다. 셰이프 코호몰로지(sheaf cohomology)는 복잡한 기하학에서 장애물을 측정하기 때문에, 한 가지 기법은 사라지는 이론들을 증명하는 것이다. 복합 기하학에서 사라지는 이론의 예로는 콤팩트한 케흘러 다지관의 선다발 공동체에 대한 고다이라 소멸 정리, 아핀 복합품종에 대한 일관성 있는 피복의 공동체에 대한 카르탄의 이론 A와 B가 있다.

복잡한 기하학은 또한 미분 기하학 및 분석에서 발생하는 기법을 이용한다. 예를 들어, 아티야-싱어 지수 정리의 특별한 경우인 히르제브루흐-리만-로흐 정리는 밑바탕이 부드러운 복합 벡터 번들의 특성 등급 측면에서 홀로모르프 벡터 번들의 홀로모르픽 오일러 특성을 계산한다.

복합 기하학에서의 분류

복잡한 기하학의 한 가지 주요 주제는 분류다. 복잡한 다지관과 품종의 경직된 특성 때문에 이러한 공간을 분류하는 문제는 종종 다루기 쉽다. 복합 기하학과 대수 기하학의 분류는 모듈리 공간의 연구를 통해 종종 발생하는데, 모듈리 공간 자체는 복합 기하학에서 발생하는 다른 기하학적 물체를 분류하는 점을 가진 복합 다지관 또는 품종이다.

리만 표면

모둘리라는 용어는 베른하르트 리만이 리만 표면에 대한 그의 원작을 하면서 만들어 졌다. 분류 이론은 콤팩트한 리만 표면으로 가장 잘 알려져 있다. 폐쇄 지향 표면의 분류에 따라 콤팩트 리만 표면은 해당 컴팩트 리만 표면의 구멍 수를 계산하는 음수가 아닌 $정수인$ g ${\displaystyle g$ 에 의해 측정되는 셀 수 있는 이산형이다.

분류는 본질적으로 획일화 정리로부터 따르며, 다음과 같다.^[2]^[3]^[4]

g = 0: $\mathbb {CP} ^{1}$ $\mathbb {CP} ^{1}$ $\mathbb {CP} ^{1}$ ${\$ }
g = 1: 속 1의 가능한 콤팩트 리만 표면, 이른바 타원 곡선, 모듈형 곡선을 분류하는 1차원 복합 다지관이 있다. 균일화 정리에서는 타원곡선을 인용 $\mathbb {C} /(\mathbb {Z} +\tau \mathbb {Z} )$ / $\mathbb {C} /(\mathbb {Z} +\tau \mathbb {Z} )$ ( $\mathbb {C} /(\mathbb {Z} +\tau \mathbb {Z} )$ + $\mathbb {C} /(\mathbb {Z} +\tau \mathbb {Z} )$ Z $\mathbb {C} /(\mathbb {Z} +\tau \mathbb {Z} )$ ) ${\displaystyle \mathb {C} /(\mathb$ { $Z}$ + $\tau \tau$ {Z $})$ 로 작성할 수 있다. 여기서 $\mathbb {C} /(\mathbb {Z} +\tau \mathbb {Z} )$ $\tau$ $\tau$ 은 엄밀하게 양의 가상적인 부분을 가진 복잡한 숫자다 $\tau$ . 모듈리 공간은 Möbius 변환에 의해 위쪽 반면에 작용하는 $\operatorname {PSL} (2,\mathbb {Z} )$ $\operatorname {PSL} (2,\mathbb {Z} )$ ⁡ $\operatorname {PSL} (2,\mathbb {Z} )$ ( $\operatorname {PSL} (2,\mathbb {Z} )$ , $\operatorname {PSL} (2,\mathbb {Z} )$ ) $\operatorname {PSL}(2,\mathb {Z} )$ 그룹의 몫으로 주어진다.
G1:각 종 한 사람보다, 로사 g컴팩트한 리만의moduli 공간 Mg{\displaystyle{{M\mathcal}}_{g}}, 치수한 C⁡ Mg)3g− 3{\displaystyle \dim_{\mathbb{C}}{{M\mathcal}}_{g}=3g-3의} 닦아냅니다. 타원 곡선의 경우와 유사하게 보다 큰, 이 공간은 s로 얻을 수 있uit그룹 $\operatorname {Sp} (2g,\mathbb {Z} )$ $\operatorname {Sp} (2g,\mathbb {Z} )$ ( $\operatorname {Sp} (2g,\mathbb {Z} )$ , Z $\operatorname {Sp} (2g,\mathbb {Z} )$ ) ${\displaystyle \operatorname {Sp}(2g,\mathb {Z})$ 의 작업에 의한 Sigel 상부 절반 공간의 가능한 지수 $\operatorname {Sp} (2g,\mathbb {Z} )$

홀로모르프 라인 번들

복잡한 기하학은 복잡한 공간뿐만 아니라 그것들에 부착된 다른 홀로모픽 오브젝트와 관련이 있다. 복합 버라이어티 $X$ ${\displaystyle X$ $\operatorname {Pic} (X)$ 의 홀로모픽 $\operatorname {Pic} (X)$ 번들의 분류는 X ${\$ $displaystyle \operatorname {Pic}(X)$ 의 $\operatorname {Pic} (X)$ X {\ $displaystyle$ X $}$ 에 $의해$ 주어진다 $X$ $X$

피카르 다양성은 $X$ $X$ 이(가) 속 g의 콤팩트한 리만 표면인 $X$ 경우 쉽게 설명할 수 있다. 즉, 이 경우 피카르 품종은 복잡한 아벨리안 품종의 분리된 결합으로, 각 품종은 0도의 분점을 선형 등가까지 분류하면서 곡선의 야코비안 품종과 이형화되어 있다. 미분기하학 용어로, 이러한 아벨리아 품종은 $(S^{1})^{2g}$ (S 1 ) $(S^{1})^{2g}$ $(S^{1})^{2g}$ ${\$ (S $^{1})^{2g}$ 에 대한 복잡한 다지관이다 $(S^{1})^{2g}$

토렐리 정리에 의해, 콤팩트한 리만 표면은 그것의 자코비안 다양성에 의해 결정되는데, 이것은 복잡한 공간에 대한 구조 연구가 유용할 수 있는 한 가지 이유를 보여준다, 그것은 그 공간을 스스로 분류할 수 있게 해 줄 수 있다는 것이다.

참고 항목

참조

^ Voisin, C, 2016. 호지 추측. 수학의 개방형 문제(pp. 521-543). 스프링거, 참.
^ Forster, O. (2012). Riemann 표면에 대한 강의 (Vol. 81). 스프링거 사이언스 & 비즈니스 미디어.
^ 미란다, R.(1995) 대수 곡선 및 리만 표면(Vol. 5). 미국 수학 협회
^ 도날드슨, S. (2011년) 리만 표면 옥스퍼드 대학 출판부

Huybrechts, Daniel (2005). Complex Geometry: An Introduction. Springer. ISBN 3-540-21290-6.
Griffiths, Phillip; Harris, Joseph (1994), Principles of algebraic geometry, Wiley Classics Library, New York: John Wiley & Sons, ISBN 978-0-471-05059-9, MR 1288523
Hörmander, Lars (1990) [1966], An Introduction to Complex Analysis in Several Variables, North–Holland Mathematical Library, 7 (3rd (Revised) ed.), Amsterdam–London–New York–Tokyo: North-Holland, ISBN 0-444-88446-7, MR 1045639, Zbl 0685.32001
S. 코바야시, K. 노미즈. 미분 기하학의 기초 (Wiley Classic Library) 제1, 2권.
E . H. 네빌(1922) 삼차원의 비등방성 유클리드 공간에서의 해석 기하학으로의 프로레고메나.

[1] Voisin, C, 2016. 호지 추측. 수학의 개방형 문제(pp. 521-543). 스프링거, 참.

[2] Forster, O. (2012). Riemann 표면에 대한 강의 (Vol. 81). 스프링거 사이언스 & 비즈니스 미디어.

[3] 미란다, R.(1995) 대수 곡선 및 리만 표면(Vol. 5). 미국 수학 협회

[4] 도날드슨, S. (2011년) 리만 표면 옥스퍼드 대학 출판부

[1]

[2]

[3]

[4]

show 권한통제
일반	통합 권한 파일(독일)
기타	마이크로소프트 어학

Search