중심

삼각형의 중심

수학과 물리학에서 평면 도형의 중심 또는 기하학적 중심은 도형의 모든 점의 산술 평균 위치입니다.비공식적으로,^[1] 핀 끝의 모양(질량이 균일하게 분포된)의 컷아웃이 완벽하게 균형을 이룰 수 있는 지점입니다.동일한 정의는 n차원 ^[2]공간의 모든 물체로 확장됩니다.

기하학에서 barycenter라는 단어는 중심과 동의어이고, 천체물리학 및 천문학에서 barycenter는 서로를 공전하는 두 개 이상의 물체의 질량 중심입니다.물리학에서 질량 중심은 국소 밀도 또는 특정 무게에 의해 가중된 모든 점의 산술 평균입니다.물리적 물체의 밀도가 균일한 경우 질량 중심은 모양 중심과 동일합니다.

지리학에서 해수면에 대한 지구 표면 영역의 반경 투영 중심은 그 지역의 지리적 중심이다.

역사

"중심"이라는 용어는 최근의 동전(1814)^{[citation needed]}이다.이 용어는 "중력 중심"과 "질량의 중심"이라는 옛 용어 대신 사용되며, 이는 해당 지점의 순수 기하학적 측면이 강조되어야 할 때 사용됩니다.그 용어는 영어 특유의 것이다.프랑스인들은 대부분의 경우 "centre de gravité"를 사용하고 다른 사람들은 비슷한 의미의 용어를 사용합니다.

이름에서 알 수 있듯이 무게중심은 기계학에서 생겨난 개념으로, 아마도 건축 활동과 관련이 있을 것입니다.언제, 어디서, 누구에 의해 발명되었는지는 알려지지 않았다. 왜냐하면 그것은 작은 차이와 함께 많은 사람들에게 개별적으로 떠올랐을 가능성이 있기 때문이다.

아르키메데스는 그 명제를 명시적으로 언급하지 않았지만, 간접적으로 언급하면서 그가 그것에 익숙했음을 암시한다.하지만, 수학의 첫 번째 역사(1758)의 저자인 장-에티엔 몽투클라 (1725–1799)는 고체의 무게 중심이 아르키메데스가 다루지 않은 주제라고 단정적으로 선언한다.

1802년 샤를 보수트 (1730–1813)는 두 권으로 이루어진 에사이 수르 레네랄 데 마테마티크를 출판했습니다.이 책은 출간된 지 2년 만에 이탈리아어(1802-03년), 영어(1803년), 독일어(1804년)로 이미 번역이 된 것으로 보아 그의 동시대인들은 이 책을 높이 평가했다.보수트는 아르키메데스가 평면 도형의 중심을 찾아냈다고 믿지만,^[3] 고체에 대해서는 할 말이 없다.

유클리드가 아르키메데스 (기원전 287–212년)의 어린 시절에도 알렉산드리아에서 활동했을 가능성이 있지만, 아르키메데스가 알렉산드리아를 방문했을 때, 유클리드는 더 이상 그곳에 없었다.따라서 아르키메데스는 삼각형의 중위수가 점(삼각형의 무게 중심)에서 만나는 정리를 유클리드로부터 직접 배울 수 없었을 것이다. 왜냐하면 이 명제는 유클리드 원소에 없기 때문이다.이 명제의 첫 번째 명시적 진술은 알렉산드리아의 헤론(아마 1세기)에 기인하며 그의 역학에서 나타난다.19세기까지는 평면 기하학 교과서에 그 명제가 보편화되지 않았다는 것이 덧붙여질 수 있다.

특성.

볼록한 물체의 기하학적 중심은 항상 물체에 있다.볼록하지 않은 물체는 그림 자체 외부에 있는 중심을 가질 수 있습니다.예를 들어 반지나 그릇의 중심은 물체의 중심 보이드에 있습니다.

중심점이 정의되어 있으면 대칭 그룹에 있는 모든 등각선의 고정점이 됩니다.특히, 물체의 기하학적 중심은 대칭의 모든 초평면의 교차점에 있습니다.많은 도형(정다각형, 정다면체, 원통, 직사각형, 마름모꼴, 원, 구, 타원, 타원체, 초평형, 초평형 등)의 중심은 이 원리로만 판단할 수 있다.

특히 평행사변형의 중심은 두 대각선의 만남점이다.이것은 다른 4변수에는 해당되지 않는다.

같은 이유로, 변환에는 고정점이 없기 때문에, 변환 대칭을 가지는 객체의 중심은 정의되지 않습니다(또는 둘러싸인 공간 밖에 있습니다.

예

삼각형의 중심은 삼각형의 세 중위수(정점과 반대편의 ^[4]중간점을 연결하는 각 중위수)의 교차점입니다.

삼각형의 중심에 대한 다른 속성은 아래를 참조하십시오.

위치 설정

수직선법

아래 그림 (a)와 같이 균일한 밀도 평판 라미나의 중심은 동일한 형상을 가진 균일한 밀도의 얇은 물체의 결합 질량 중심을 구하기 위해 납선과 핀을 사용하여 실험적으로 결정할 수 있다.본체는 핀에 의해 고정되며, 핀 주위를 자유롭게 회전할 수 있도록 추정된 중심에서 벗어난 위치에 삽입됩니다. 그런 다음 핀에서 수직선이 떨어집니다(그림 b).표면에서 수직선의 위치가 추적되고, 개체의 중심에서 벗어난 다른 점(또는 여러 점)에 핀을 삽입한 상태에서 절차가 반복됩니다.이러한 선의 고유한 교차점은 중심입니다(그림 c).본체의 밀도가 균일한 경우, 이렇게 만들어진 모든 선은 중심을 포함하며 모든 선은 정확히 동일한 위치에서 교차합니다.


(a)	(b)	(c)

이 방법은 (이론적으로) 중심부가 형상의 바깥쪽에 있을 수 있는 오목한 모양과 실질적으로 중심부가 몸 안에 있을 수 있는 (균일한 밀도의) 고체까지 확장될 수 있습니다.수직선의 (가상) 위치는 형상을 따라 그리는 방법 이외의 방법으로 기록해야 합니다.

밸런스 방식

볼록한 2차원 형상의 경우 좁은 원통 꼭대기와 같은 작은 형상에서 형상의 균형을 잡아 중심을 찾을 수 있다.중심은 두 도형 사이의 접촉 범위 내(그리고 도형이 핀 위에서 균형을 이루는 지점)에서 발생합니다.원칙적으로 점차적으로 좁은 실린더를 사용하여 임의의 정밀도로 중심을 찾을 수 있다.실제로는 기류가 이를 불가능하게 만든다.그러나 여러 밸런스에서 겹치는 범위를 표시함으로써 상당한 수준의 정확도를 달성할 수 있다.

유한한 점 집합의

$\mathbb {R} ^{n}$ n $\mathbb {R} ^{n}$ \ $displaystyle$ $\mathbb {R}^{n}$ 의 $\mathbb {R} ^{n}$ ^[2] $\mathbb {R} ^{n}$ ${\$ $displaystyle$ 의 $\mathbf {x} _{1},\mathbf {x} _{2},\ldots ,\mathbf {x} _{k}$ 유한 $\mathbf {x} _{1},\mathbf {x} _{2},\ldots ,\mathbf {x} _{k}$ 의 중심은 다음과 같습니다.

\mathbf {C} = flac {mathbf {x} _{1} + \mathbf {x} + \cdots + \mathbf {x} _{k}}}.

이 점은 그 자체와 집합의 각 점 사이의 유클리드 거리 제곱의 합을 최소화합니다.

기하학적 분해에 의해

$평면도형$ X({ $displaystyle$ $X$ })의 $X$ 중심은 한정된 수의 $단순$ 한 $X_{1},X_{2},\dots ,X_{n}$ $X_{1},X_{2},\dots ,X_{n}$ 로 나누어 계산할 수 있으며, 각각의 $C_{i}$ $({$ 와 $A_display$ A_ ${n$ $}$ 의 $C_{i}$ $A_{i}$ $A_{i}$ 입니다.할 수 없다

{\displaystyle C_{x}=subfrac {c_{i}_{x}A_{i}}{\sum_{i}A_{i}}, C_{y}=440frac({sum_{i}{C_{i}}_{y})A_{i}}{\sum _{i}A_{i}}}}:

$X$ 의 $X$ 구멍, 부품 $사이$ 에 겹치는 구멍, 또는 그림 밖으로 뻗어나가는 부품은 모두 $A_{i}$ 의 $A_{i}$ Ai ${$ $i$ 즉 Ai{ $displaystyle A_{i}$ 를 $A_{i}$ 사용하여 처리할 수 있습니다. 즉, $A_{i}$ 는 부호의 합이 되도록 음의 부호를 사용하여 실시해야 합니다. $A_{i}$ $p$ 를 $p$ 둘러싸는 모든 부분의 i ${$ $displaystyle$ $A_{i}$ 는 $A_{i}$ p $\displaystyle$ p가 $p$ X $(\displaystyle$ X $X$ 에 속하는 $경우$ 1이고, 그렇지 않은 경우 0입니다.

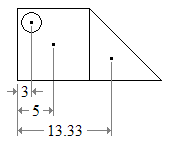
예를 들어 (a) 아래의 그림은 양의 면적을 가진 정사각형과 삼각형과 음의 면적을 가진 원형 구멍으로 쉽게 분할할 수 있다.

(a) 2D 객체

(b) 보다 단순한 요소를 사용하여 기술한 물체

다. 물체 요소의 중심

각 부품의 중심은 단순한 모양의 중심 리스트에서 찾을 수 있습니다(c).그런 다음 그림의 중심은 세 점의 가중 평균입니다.그림의 왼쪽 가장자리에서 중심부의 수평 위치는 다음과 같습니다.

({displaystyle x=pic frac {5\times 10^{2}+13.33\times \frac {1}{2}-3\times \pi 2.5^{2}){10^{2}-\pi 2.5^{2}}\text}).}

중심부의 수직 위치는 동일한 방식으로 찾을 수 있습니다.

모든 3차원 물체에 동일한 공식이 적용되지만 각 $($ 디스플레이 $스타일$ A_ ${i$ })는 $A_{i}$ 면적이 아닌 $($ X_ ${i$ 의 부피가 되어야 합니다.또한 모든 $d$ 에 $\mathbb {R} ^{d}$ R $\mathbb {R} ^{d}$ d \ $displaystyle$ $\mathbb {R}$ $d$ ^{ $d$ $}}$ 의 서브셋에 대해서도 고정되며, 영역은 $d$ 의 d\ $displaystyle$ d $}$ 치수 $d$ 측도로 대체됩니다.

적분식별

$\mathbb {R} ^{n}$ n $(\$ ^{ $n})$ 의 $\mathbb {R} ^{n}$ 부분 집합 X의 중심은 적분으로도 계산할 수 있다.

C=blac {\int xg(x)\;blac} {\int g(x)\;blac

여기서 적분은 전체

\mathbb {R} ^{n}

\mathbb {R} ^{n}

n

(\

^{

n

에 걸쳐 취해지고 g는 부분 집합의 특성 함수이며, X 안쪽은 1이고 바깥쪽은 ^[5]0입니다.분모는 단순히 집합 X의 척도입니다.집합 X의 측정값이 0이거나 적분이 분산된 경우에는 이 공식을 적용할 수 없습니다.

중심체의 또 다른 공식은

C_{k}=blac {int zS_{k}(z)\;dz}{\int g(x)\;blac}

여기서_k C는 C의 k번째 좌표이고, S_k(z)는 X와 초평면의 교차점에 대한 측도이며, x = z라는 공식으로_k 정의된다.다시 말하지만, 분모는 단순히 X의 척도이다.

특히 평면 도형의 경우 중심 좌표는 다음과 같습니다.

C_{\mathrm {x} } = prac {int xS_{\mathrm {y} }(x)\;param} {displaystyle C_{\mathrm {x}A}}

C_{\mathrm {y} = frac {int yS_{\mathrm {x} }(y)\;dy} {A}}

여기서 A는 그림 X의 면적이고_y, S(x)는 가로 방향 x에서 수직선과 X의 교차점 길이이며, S_x(y)는 교환된 축에 대한 유사한 양이다.

유계 영역의

$[a,b]$ $f(x)\geq g(x)$ ( $f(x)\geq g(x)$ ) $f(x)\geq g(x)$ g $f(x)\geq g(x)$ ( $f(x)\geq g(x)$ x ) \ $displaystyle$ f) $({\bar {x}},\;{\bar {y}})$ $、$ g ( $f(x)\geq g(x)$ ) \ $displaystyle$ $[a,b]$ f ( x )\ $displaystyle$ f ( $x$ )\ $geq$ g( $x$ )와 $({\bar {x}},\;{\bar {y}})$ $f(x)\geq g(x)$ $같이$ 연속 $함수$ f ( \ $displaystyle$ f )그래프로 $f$ $g$ 둘러싸인 영역의 중심 $x$ $({\bar {x}},\;{\bar {y}})$ $y$ $）$ 。 $a\leq x\leq b$ {\ $displaystyle a\leq x\leq$ b $a\leq x\leq b$ 는^[5]^[6] 다음과 같습니다 $.$

{x}}=syslogfrac {1}{A}}\int _{a}^{b}x[f(x)-g(x)]\;dx

{y}}=syslogfrac {1}A}}\int _{a}^{b}\left[{\frac {f(x)+g(x)}{2}\right][f(x)-g(x)]\;dx,

$A$ 서A(\ $displaystyle$ A $)$ 는 $A$ 영역 영역입니다 ${\textstyle \int _{a}^{b}\left[f(x)-g(x)\right]dx}$ b ${\textstyle \int _{a}^{b}\left[f(x)-g(x)\right]dx}$ ${\textstyle \int _{a}^{b}\left[f(x)-g(x)\right]dx}$ ( ${\textstyle \int _{a}^{b}\left[f(x)-g(x)\right]dx}$ x ${\textstyle \int _{a}^{b}\left[f(x)-g(x)\right]dx}$ ) - ${\textstyle \int _{a}^{b}\left[f(x)-g(x)\right]dx}$ ( ${\textstyle \int _{a}^{b}\left[f(x)-g(x)\right]dx}$ ) ${\textstyle \int _{a}^{b}\left[f(x)-g(x)\right]dx}$ ] ${\textstyle \int _{a}^{b}\left[f(x)-g(x)\right]dx}$ x { $textstyle \int$ _ { $a$ }^{ $b}\left [f(x)-g(x)\right ]dx$ ^[7]^[8]）。

Integraph 포함

Integraph(평면계의 친척)는 평활(또는 분할적으로 매끄러운) 경계를 가진 불규칙한 모양의 물체의 중심을 찾기 위해 사용할 수 있다.관련된 수학적 원리는 그린의 ^[9]정리의 특별한 경우이다.

L자형 물체의

L자형 물체의 중심을 결정하는 방법입니다.

그림 2와 같이 2개의 직사각형으로 분할한다.대각선을 그려서 이 두 직사각형의 중심을 구하세요.중심을 연결하는 선을 긋는다.모양의 중심은 이 선 AB 위에 있어야 합니다.
그림 3과 같이 모양을 두 개의 다른 직사각형으로 나눕니다.대각선을 그려서 이 두 직사각형의 중심을 구하세요.중심을 연결하는 선을 긋는다.L자형의 중심은 이 선 CD 위에 있어야 합니다.
형상의 중심은 AB와 CD를 따라 있어야 하므로 두 선의 교차점인 O에 있어야 합니다.점 O는 L자형 물체의 내부 또는 외부에 있을 수 있습니다.

삼각형의

삼각형의 중심은 삼각형의 중간점(각 정점과 반대편의 ^[4]중간점을 연결하는 선)의 교차점입니다.중심은 각 중위수를 2:1 비율로 나눕니다. 즉, 각 변에서 반대 정점까지의 거리의 θ에 위치합니다(오른쪽 ^[10]^[11]그림 참조).그 데카르트 좌표는 세 꼭지점의 좌표의 평균이다.즉, 3개의 정점이 $L=(x_{L},y_{L}),$ $L=(x_{L},y_{L}),$ ( $L=(x_{L},y_{L}),$ L , $L=(x_{L},y_{L}),$ ) $L=(x_{L},y_{L}),$ , { $displaystyle$ L $=$ ( $x M$ , y $M=(x_{M},y_{M}),$ { L } ) , { L } , $}$ $L=(x_{L},y_{L}),$ $M=(x_{M},y_{M}),$ $M=(x_{M},y_{M}),$ ( $M=(x_{M},y_{M}),$ M , $M=(x_{M},y_{M}),$ ) , $M=(x_{M},y_{M}),$ \ $display$ M = ( x $_ { M$ , $N=(x_{N},y_{N}),$ $}$ ) $N=(x_{N},y_{N}),$ N $=$ ( $N=(x_{N},y_{N}),$ , $N=(x_{N},y_{N}),$ ) $N=(x_{N},y_{N}),$ 、 $displaysty style$ N ) $N=(x_{N},y_{N}),$ 。

C=cfrac {1}{3}}(L+M+N)=\left({\frac {1}{3})(x_{L}+x_{M}+x_{N}),\;{\frac {1}{3}}(y_{})L}+y_{M}+y_{N}\right).

따라서 중심은 $($ 스타일 ${tfrac {1}{3}):$ ${1}{3}:$ 중심 ${\tfrac {1}{3}}:{\tfrac {1}{3}}:{\tfrac {1}{3}}$ 좌표로 $표시됩니다.$

삼선형 좌표에서 중심은 변 길이 a, b, c 및 정점 각도 L, M, ^[12]N의 관점에서 다음과 같은 방법으로 표현할 수 있다.

디스플레이 스타일C&=bcfrac {1}{a}:\frac {1}{b}:\frac {c}}=bc:ca:ab=\csc L:\csc M:\[6pt]&=\cos L+\cos M\cdot \cos N:\cos \cos \cdot \cos \cos \c\c\c\cos \cos \c\cos \cos \cos \cos \cos \c\c\cos \c\c\cos \cos \cos \cos \cos \c\c\end { aligned}}

삼각형이 균일한 재료 시트로 만들어지거나 모든 질량이 3개의 정점에 집중되어 있고 그 사이에 균등하게 나누어져 있는 경우 중심은 물리적 질량 중심이기도 합니다.반면 질량이 삼각형의 둘레를 따라 균일한 선형 밀도로 분포되어 있는 경우 질량의 중심은 Spiker 중심(일반적으로 전체 삼각형의 기하학적 중심과 일치하지 않는 중앙 삼각형의 유도 요소)에 있습니다.

삼각형의 면적은 변의 길이와 변에서 ^[13]중심까지의 수직 거리의 1.5배이다.

삼각형의 중심은 직교 중심 H와 원주 중심 O 사이의 오일러 선 위에 있으며,^[14]^[15] 직교 중심 H와 원주 중심 O 사이의 오일러 선에 전자보다 정확히 두 배 가까이 있다.

(\displaystyle {CH}}=2\displaystyle {CO}).}

또한 인센티브 I 및 9점 센터 N의 경우,

{\overline {CH}}&=4{\overline {CN}\[5pt]{\overline {CO}}&=2{\overline {CN}\[5pt]{\overline {\overline}IC}}&<{\overline {HC}}\[5pt]{\overline {\overline}IH}}&<{\overline {HC}}\[5pt]{\overline {\overline}IC}} & < { \ overline { }IO}}\end {aligned}

G가 삼각형 ABC의 중심인 경우:

\displaystyle({\text{Area of }}\text{Area of }}\text{ACG})=display\text{Area of }}\text{BCG})=displayfrac {1}{3}{\text{Area of }\mathrm} {AC})

삼각형의 중심 등교 켤레는 삼각형의 심미디언 점입니다.

중심을 통과하는 세 개의 중위수 중 하나는 삼각형의 면적을 반으로 나눕니다.이것은 중심을 통과하는 다른 선에는 해당되지 않습니다. 등면적 분할에서 가장 큰 이탈은 중심을 통과하는 선이 삼각형의 한 변에 평행하여 더 작은 삼각형과 사다리꼴을 만들 때 발생합니다. 이 경우 사다리꼴의 면적은 원래 ^[16]삼각형의 5/9입니다.

P를 꼭지점 A, B, C와 중심 G가 있는 삼각형의 평면에 있는 임의의 점이라고 하자.그러면 세 정점에서 P의 거리 제곱의 합이 정점에서 중심 G의 거리 제곱의 합을 P와 ^[17]G 사이의 거리 제곱의 3배 초과한다.

PA^{2}+PB^{2}+PC^{2}=GA^{2}+GB^{2}+GC^{2}+3PG^{2}

삼각형의 변의 제곱합은 ^[17]정점으로부터의 중심 거리 제곱의 3배입니다.

({displaystyle AB^{2}+BC^{2}+CA^{2}=3(GA^{2}+GB^{2}+GC^{2}).}

삼각형의 중심은 삼각형의 측면에서 ^[18]점의 방향 거리 곱을 최대화하는 점입니다.

ABC를 삼각형, G를 중심, D, E, F를 각각 BC, CA, AB의 중간점으로 하자.ABC^[19] 평면의 임의의 점 P에 대하여

(\display style PA+PB+)PC\leq 2(PD+)PE+PF)+3페이지}

폴리곤의

n개의 꼭지점(x₀,y₀), (x₁,y₁), ..., (x_n−1,y_n−1)에 의해 정의된 비자기 교차 닫힌 폴리곤의 중심은 점(C_x,C_y)^[20]이다.

{\displaystyle C_{\mathrm {x} } = flac {1} {6A}}\sum _{i=0}^{n-1}(x_{i}+x_{i+1})(x_{i}\y_{i+1}-x_{i+1}\y_{i}),},

그리고.

{\displaystyle C_{\mathrm {y} } = flac {1} {6A}}\sum _{i=0}^{n-1}(y_{i}+y_{i+1})(x_{i}\y_{i+1}-x_{i+1}\y_{i}),},

여기서 A는 구두끈 공식에 따라 폴리곤의 부호 ^[20]영역입니다.

({displaystyle A=param frac {1}{2}}\sum _{i=0}^{n-1}(x_{i}\y_{i+1}-x_{i+1}\y_{i}).}

만약 포인트 시계 방향으로 o.에 번호가 부여된다 이러한 식에서, vertices 그들의 발생 순서대로 다각형의 주변을 따라 얼마 남지 않게 되기만, 꼭지점(xn, yn)이(x0, y0)과 동일한 것을, 나는 지난 사건을 1{\displaystyle를 i+1}+ 의미한 것으로 추정은 약 나에=0{\displaystyle i=0}반복 반복 반복 반복 재생해야 한다.(가정한다rder, 위와 같이 계산된 영역 A는 음이 되지만, 이 경우에도 중심 좌표는 정확합니다.)

원뿔 또는 피라미드의

원뿔 또는 피라미드의 중심은 정점과 베이스의 중심을 연결하는 선분에 있습니다.솔리드 콘 또는 피라미드의 경우 중심은 베이스에서 정점까지의 거리의 1/4입니다.밑면이 없는 껍데기(홀로우)인 원뿔 또는 피라미드의 경우 중심은 밑면에서 정점까지의 거리의 1/3입니다.

사면체 및 n차원 단순체의 경우

4면체는 4개의 삼각형을 면으로 하는 3차원 공간의 물체이다.사면체의 정점과 반대면의 중심을 연결하는 선분을 중앙값이라고 하고, 반대편 두 모서리의 중간점을 연결하는 선분을 쌍방향값이라고 한다.그래서 4명의 중간자와 3명의 바이메디안이 있습니다.이 7개의 선분들은 모두 사면체의 ^[21]중심에서 만난다.중위수는 3:1의 비율로 구심으로 나뉩니다.사면체의 중심은 Monge 점과 원주점(외접된 구의 중심) 사이의 중간점입니다.이 세 점은 삼각형의 오일러 선과 유사한 사면체의 오일러 선을 정의합니다.

이러한 결과는 다음과 같은 방법으로 모든 n차원 심플렉스로 일반화된다.심플렉스의 정점 집합이 v ${v_{0},\ldots ,v_{n}}$ ${v_{0},\ldots ,v_{n}}$ ${v_{0},\ldots ,v_{n}}$ {\ $displaystyle$ { $v_{0},\ldots,v_{n$ 인 경우 정점을 벡터로 간주하면 중심은 다음과 같습니다.

{{displaystyle C=paramfrac {1}{n+1}}\sum _{i=0}^{n}v_{i}.}

질량이 심플렉스 전체에 균일하게 분포되어 있거나 N+1의 동일한 질량으로 정점에 집중되어 있는 경우 기하학적 중심은 질량의 중심과 일치합니다.

반구의

고체 반구의 중심(즉, 고체 공의 절반)은 구체의 중심과 반구의 극을 연결하는 선분을 3:5 비율로 나눈다(즉, 중심에서 극으로 가는 길의 3/8).중공 반구의 중심(즉, 중공 구의 절반)은 구의 중심과 반구의 극을 연결하는 선분을 반으로 나눕니다.

「」를 참조해 주세요.

메모들

^ 프로터 & 모레이 주니어(1970, 521)
^ ^a ^b 프로터 & 모레이 주니어(1970년, 520페이지)
^ Court, Nathan Altshiller (1960). "Notes on the centroid". The Mathematics Teacher. 53 (1): 33–35. doi:10.5951/MT.53.1.0033. JSTOR 27956057.
^ ^a ^b 알트실러 코트 (1925, 페이지 66)
^ ^a ^b 프로터 & 모레이 주니어(1970년, 페이지 526)
^ 프로터 & 모레이 주니어(1970년, 페이지 527)
^ 프로터 & 모레이 주니어(1970년, 528페이지)
^ 라슨(1998, 페이지 458-460)
^ 상윈
^ 알트실러 코트 (1925, 페이지 65)
^ 케이 (1969년, 페이지 184년)
^ 클라크 킴벌링의 삼각형 백과사전
^ 존슨 (2007, 페이지 173)
^ 알트실러 코트 (1925, 페이지 101)
^ 케이 (1969년, 페이지 18, 189년, 225년–226년)
^ Bottomley, Henry. "Medians and Area Bisectors of a Triangle". Retrieved 27 September 2013.
^ ^a ^b 알트실러 코트 (1925년, 페이지 70-71)
^ Kimberling, Clark (201). "Trilinear distance inequalities for the symmedian point, the centroid, and other triangle centers". Forum Geometricorum. 10: 135–139.
^ 제럴드 A.에드거, 다니엘 H. 울만 & 더글라스 B.West (2018) 문제와 해결책, American Mathemical Monthly, 125:1, 81-89, DOI: 10.1080/00029890.2018.1397465
^ ^a ^b 부르크(1997년)
^ 렁, 금팀, 수은, "벡터, 행렬, 기하학", 홍콩대학교 출판부, 1994, 53-54페이지

레퍼런스

Altshiller-Court, Nathan (1925), College Geometry: An Introduction to the Modern Geometry of the Triangle and the Circle (2nd ed.), New York: Barnes & Noble, LCCN 52013504
Bourke, Paul (July 1997). "Calculating the area and centroid of a polygon".
Johnson, Roger A. (2007), Advanced Euclidean Geometry, Dover
Kay, David C. (1969), College Geometry, New York: Holt, Rinehart and Winston, LCCN 69012075
Larson, Roland E.; Hostetler, Robert P.; Edwards, Bruce H. (1998), Calculus of a Single Variable (6th ed.), Houghton Mifflin Company
Protter, Murray H.; Morrey, Jr., Charles B. (1970), College Calculus with Analytic Geometry (2nd ed.), Reading: Addison-Wesley, LCCN 76087042
Sangwin, C.J., Locating the centre of mass by mechanical means (PDF), archived from the original (PDF) on November 13, 2013

외부 링크

Weisstein, Eric W. "Geometric Centroid". MathWorld.
클락 킴벌링의 트라이앵글 센터 백과사전.중심은 X(2)로 색인화된다.
절개 코트에서 중심 특성
나침반과 직선 모서리가 있는 삼각형의 중심과 중심 구조를 보여주는 대화형 애니메이션
Dynamic Geometry Sketchs에서 삼각형의 중앙점과 중심을 실험적으로 찾아낸 신데렐라의 중력 시뮬레이터를 이용한 인터랙티브 다이내믹 지오메트리 스케치.

[1] 프로터 & 모레이 주니어(1970, 521)

[protter520-2] 프로터 & 모레이 주니어(1970년, 520페이지)

[3] Court, Nathan Altshiller (1960). "Notes on the centroid". The Mathematics Teacher. 53 (1): 33–35. doi:10.5951/MT.53.1.0033. JSTOR 27956057.

[altshiller66-4] 알트실러 코트 (1925, 페이지 66)

[protter526-5] 프로터 & 모레이 주니어(1970년, 페이지 526)

[6] 프로터 & 모레이 주니어(1970년, 페이지 527)

[7] 프로터 & 모레이 주니어(1970년, 528페이지)

[8] 라슨(1998, 페이지 458-460)

[9] 상윈

[10] 알트실러 코트 (1925, 페이지 65)

[11] 케이 (1969년, 페이지 184년)

[12] 클라크 킴벌링의 삼각형 백과사전

[13] 존슨 (2007, 페이지 173)

[14] 알트실러 코트 (1925, 페이지 101)

[15] 케이 (1969년, 페이지 18, 189년, 225년–226년)

[Bottomley2002-16] Bottomley, Henry. "Medians and Area Bisectors of a Triangle". Retrieved 27 September 2013.

[altshiller70-17] 알트실러 코트 (1925년, 페이지 70-71)

[18] Kimberling, Clark (201). "Trilinear distance inequalities for the symmedian point, the centroid, and other triangle centers". Forum Geometricorum. 10: 135–139.

[19] 제럴드 A.에드거, 다니엘 H. 울만 & 더글라스 B.West (2018) 문제와 해결책, American Mathemical Monthly, 125:1, 81-89, DOI: 10.1080/00029890.2018.1397465

[:0-20] 부르크(1997년)

[21] 렁, 금팀, 수은, "벡터, 행렬, 기하학", 홍콩대학교 출판부, 1994, 53-54페이지

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

Search

중심

네임스페이스

더

목차

역사

특성.

예

위치 설정