외각정리

Exterior angle theorem

외각 정리는 유클리드 원소의 제안 1.16으로, 삼각형의 외각 측도가 원격 내부 각도의 측도 중 하나보다 크다고 기술하고 있다. 이것은 절대 기하학의 근본적인 결과인데, 그 증거는 평행한 가정법에 의존하지 않기 때문이다.

몇몇 고등학교 기하학 치료에서, "외각 정리"라는 용어는 다른 결과,[1] 즉 삼각형의 외부 각도의 측정치가 원격 내부 각도의 측정값의 합계와 동일하다는 제안 1.32의 부분에 적용되었다. 유클리드 평행에 따라 달라지는 이 결과는 유클리드 외부각 정리(HSEAT)와 구별하기 위해 "고등학교 외부각 정리"(High School External angle orgment, HSEAT)라고 한다.

일부 저자는 '고교 외각 정리'를 외각 정리의 강한 형태라고 하고, '유클리드 외각 정리'를 약체로 언급한다.[2]

외부 각도

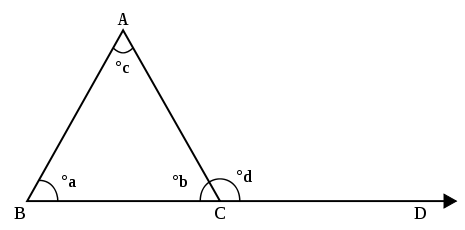
삼각형은 정점이라고 불리는 세 개의 모서리를 가지고 있다. 정점에서 함께 오는 삼각형(선 세그먼트)의 변은 두 각(선 세그먼트 대신 삼각형의 변을 선으로 간주하는 경우 네 각)을 형성한다.[3] 이러한 각 중 하나만 그 내부에 있는 삼각형의 세 번째 면을 포함하고 있으며, 이 각도를 삼각형의 내부 각이라고 한다.[4] 아래 그림에서 각 abABC, bcBCA, cCAB는 삼각형의 세 내부 각이다. 외부 각도는 삼각형의 한 측면을 확장하여 형성된다. 확장된 측면과 다른 측면 사이의 각도는 외부 각이다. 사진에서 각도 ∠ACD는 외각이다.

Remint3.svg

유클리드 외부 각도 정리

유클리드에게 주어진 발의안 1.16의 증명은 유클리드에게 결함이 있는 증거를 주는 한 곳으로 자주 인용된다.[5][6][7]

유클리드에서는 다음과 같이 외부 각도 정리를 증명한다.

  • 세그먼트 AC의 중간점 E를 구성한다.
  • 레이 BE를 그린다.
  • E가 B와 F의 중간점이 되도록 레이 BE에 F 점을 구성한다.
  • 부문별 FC를 추첨하다

일치 삼각형을 통해 우리는 we BAC = ∠ ECF 및 ∠ ECF가 ∠ ECD보다 작다고 결론을 내릴 수 있으며, ∠ ECD = ∠ ACD 따라서 ∠ BAC는 ∠ ACD보다 작으며 BC를 이등분하여 ∠ CBA 각도에 대해 동일한 작업을 수행할 수 있다.

이 결함은 점(F, 위)이 "내부" 각도(inside)"라는 가정에 있다. 이 주장에 대한 이유는 제시되지 않았지만, 동봉된 도표는 그것을 진실된 진술처럼 보이게 한다. 유클리드 기하학에 대한 전체 공리 세트를 사용할 때(기하학 기초 참조)[8] 유클리드 이 주장을 입증할 수 있다.

구면 형상에 유효하지 않음

작은 삼각형은 거의 유클리드 방식으로 동작할 수 있지만, 큰 삼각형의 밑부분에 있는 외각은 90°로 유클리드 외각 정리와는 모순된다.

외부 각도 정리는 구형 기하학이나 관련 타원형 기하학에서는 유효하지 않다. 하나의 구면 삼각형을 생각해보자. 그 중 하나는 북극이고 다른 두 개는 적도에 놓여있다. 북극(구체의 큰 원)에서 뿜어져 나오는 삼각형의 옆면은 둘 다 직각으로 적도를 만나므로 이 삼각형은 외각으로 외각은 외각으로 외각은 외각으로 외각은 외각으로 외각은 외각으로 외각은 외각으로 외각은 외각으로 원각과 같다. 다른 내부 각도(북극의 경우)는 90° 이상으로 만들 수 있어 이 성명의 실패를 더욱 강조할 수 있다. 그러나 유클리드 외각 정리는 절대 기하학의 정리이므로 쌍곡 기하학에서는 자동적으로 유효하다.

고등학교외부각정리

고등학교 외부각 정리(HSEAT)는 삼각형의 정점에서 외부각의 크기가 삼각형의 다른 두 꼭지점(원격 내부각)에서 내부각의 크기의 합계와 같다고 말한다. 사진에서 각도 ACD의 크기는 각도 ABC의 크기와 각도 CAB의 크기와 같다.

HSEAT는 삼각형의 각도의 합이 180°라는 유클리드 문장과 논리적으로 동등하다. 삼각형 각도의 측정 합계가 180°인 것으로 알려지면 HSEAT는 다음과 같이 증명된다.

반면에 HSEAT가 참된 진술로 받아들여진다면 다음과 같다.

HSEAT에 대한 증거

삼각형 각도의 측정 합계가 180°임을 증명한다.

HSEAT의 유클리드 증명(그리고 동시에 삼각형의 각도의 합계에 대한 결과)은 C 지점을 통과하는 측 AB에 평행하게 선을 구성한 다음, 그림처럼 결론을 얻기 위해 평행선의 해당 각도와 대체 내부 각도의 특성을 사용하여 시작한다.[9]

HSEAT는 삼각형에서 알 수 없는 각도의 측정값을 계산하려고 할 때 매우 유용할 수 있다.

메모들

  1. ^ Henderson & Taimiņa 2005, 페이지 110
  2. ^ Willie, 1964년 주니어, 페이지 101 & 페이지 106 (
  3. ^ 한 선 세그먼트는 초기 면과 다른 선 단자 면으로 간주된다. 각도는 초기측에서 단자측으로 시계 반대방향으로 이동하여 형성된다. 어느 선 세그먼트가 초기 측인지 선택은 임의적이므로 선 세그먼트에 의해 결정된 각도에 대해서는 두 가지 가능성이 있다.
  4. ^ 이 내부 각도를 정의하는 방법은 삼각형의 각도의 합이 180도라고 전제하지 않는다.
  5. ^ 파버 1983, 페이지 113
  6. ^ 그린버그 1974년 페이지 99
  7. ^ 베네마 2006, 페이지 10
  8. ^ 그린버그 1974년 페이지 99
  9. ^ 히스 1956년 1권 316호

참조

  • Faber, Richard L. (1983), Foundations of Euclidean and Non-Euclidean Geometry, New York: Marcel Dekker, Inc., ISBN 0-8247-1748-1
  • Greenberg, Marvin Jay (1974), Euclidean and Non-Euclidean Geometries/Development and History, San Francisco: W.H. Freeman, ISBN 0-7167-0454-4
  • Heath, Thomas L. (1956). The Thirteen Books of Euclid's Elements (2nd ed. [Facsimile. Original publication: Cambridge University Press, 1925] ed.). New York: Dover Publications.
(3권): ISBN 0-486-60088-2(볼륨 1) ISBN 0-486-60089-0(볼륨 2) ISBN 0-486-60090-4(볼륨 3)
  • Henderson, David W.; Taimiņa, Daina (2005), Experiencing Geometry/Euclidean and Non-Euclidean with History (3rd ed.), Pearson/Prentice-Hall, ISBN 0-13-143748-8
  • Venema, Gerard A. (2006), Foundations of Geometry, Upper Saddle River, NJ: Pearson Prentice Hall, ISBN 0-13-143700-3
  • Wylie Jr., C.R. (1964), Foundations of Geometry, New York: McGraw-Hill

HSEAT 참조 자료

  • 기하 교과서 - 표준 IX, Maharashtra 중등교육 위원회, Pune - 411 005, 인도
  • 지오메트리 공통 핵심, '피슨 교육: Upper Saddle River, pages2010, 171-173페이지 미국.
  • Wheater, Carolyn C. (2007), Homework Helpers: Geometry, Franklin Lakes, NJ: Career Press, pp. 88–90, ISBN 978-1-56414-936-7.