라디안
Radian| 라디안 | |
|---|---|
| 단위계 | SI 유도 단위 |
| 단위 | 각 |
| 기호. | rad 또는 r |
| 변환 | |
| 1 rad in... | ...와 같다 |
| 밀리라디안 | 1000 mrad |
| 회전하다 | 1/2회전 |
| 도 | 180°/수직 ≈ 57.296° |
| 그라디안 | 200g/106 ≈63.662g |
기호 rad로 표시되는 라디안은 각도를 측정하는 SI 단위이며 수학의 많은 영역에서 사용되는 각도 측정의 표준 단위입니다.이 단위는 이전에는 SI 보조 단위였고(1995년 해당 범주가 폐지되기 전), 라디안은 현재 SI 파생 [1]단위이다.라디안은 SI에서 1 rad = [2]1인 무차원 단위로 정의됩니다.따라서 특히 수학적인 글쓰기에서 그 기호는 종종 생략된다.
정의.
1 라디안은 [3]원의 반지름 길이와 같은 호를 가로채는 원의 중심에서 기울어진 각도로 정의됩니다.보다 일반적으로, 경사각도의 라디안 크기는 원의 반지름에 대한 원호 길이의 비율과 같다. 즉, 여기서 θ는 라디안 단위의 경사각, s는 호 길이, r은 반지름이다.직각은 정확히 1/2 라디안입니다.[4]

1회전(360도)의 라디안 크기는 전체 원주의 길이를 반지름으로 나눈 값 또는 2µr/r 또는 2µ입니다.따라서 2µ 라디안은 360도입니다.즉, 1개의 라디안은 180/µ도 [5]57 57.295779513082320876도입니다.
2µ rad = 360°의 관계는 원호 길이의 공식, r ( 360θ _}}= r}{360}}}\과 반지름 1의 원을 사용하여 도출할 수 있다라디안은 원의 반지름과 같은 길이의 호를 따르는 각도이므로 ( 1 360µ) { 1 \ \{ text { rad } { ^ { \ } } \ }이는 1 360 ({ 1= {360text으로 더욱 단순화할 수 있다. 양측에 360°를 곱하면 360° = 2µ rad가 된다.
단위 기호
국제도량형국(International Bureau of Weights and[4] Measure)과 국제표준화기구(International Organization for[6] Standardization)는 라디안의 기호로 rad를 지정한다.100년 전에 사용된 대체 기호는 ('원형 측정'을 나타내는 문자 c), 문자 r 또는 문자 [7]r입니다. 그러나 이러한 변형은 도 기호(°) 또는 반지름(r)으로 오인될 수 있기 때문에 자주 사용되지 않습니다.따라서 1.2라디안의 값은 일반적으로 1.2라디안이라고 쓰입니다.다른 표기법에는radc 1.2rR, 1.2, 1.2 또는 1.2가 포함됩니다.
수학적인 글쓰기에서는 기호 "rad"가 생략되는 경우가 많다.기호가 없는 각도를 수량화할 때는 라디안이 사용되고, 도를 의미하는 경우에는 도 기호 °가 사용됩니다.
변환
| 회전하다 | 라디안 | 도 | 그라디언 또는 GON |
|---|---|---|---|
| 0회전 | 0라드 | 0° | 0g |
| 1/24 회전 | µ/12 rad | 15° | 16+2/3g |
| 1/16 회전 | µ/8 rad | 22.5° | 스물다g |
| 1/12 회전 | µ/6 rad | 30° | 33+1/3g |
| 1/10 회전 | µ/5 rad | 36° | 사십g |
| 1/8 회전 | µ/4 rad | 45° | 오십g |
| 1/2회전 | 1라드 | c. 57.3° | c. 63.7g |
| 1/6 회전 | µ/3 rad | 60° | 66+2/3g |
| 1/5 회전 | 2µ/5 rad | 72° | 팔십g |
| 1/4 회전 | µ/2 rad | 90° | 백g |
| 1/3 회전 | 2µ/3rad | 120° | 133+1/3g |
| 2/5 회전 | 4µ/5 rad | 144° | 160g |
| 1/2 회전 | δ rad | 180° | 이백g |
| 3/4 회전 | 3µ/2 rad | 270° | 300개g |
| 1회전 | 2광자 레이드 | 360° | 400g |
라디안과 도 사이의 변환
앞에서 설명한 바와 같이 1 라디안은 / { { { \} / { \ 입니다따라서 라디안에서 도수로 변환하려면 180µ / { { { \ / { \을 .
예를 들어 다음과 같습니다.
반대로 도에서 라디안으로 변환하려면 / { \} / { ^ { \ 를 곱합니다.
예를 들어 다음과 같습니다.
라디안의 수를 2µ로 나누어 회전(완전 회전)으로 변환할 수 있습니다.
라디안-차수 변환 유도
원의 둘레 길이는 r(\ 2r로 표시됩니다.서 rr은 원의 반지름입니다.
따라서 다음과 같은 동등한 관계가 성립합니다.
r 2 { \ 360 ^ { \ r \ \ r} [완전한 원을 그리려면 360 \ 360 ^ { \ 가 필요하기 때문에]
라디안의 정의에 따르면, 완전한 원은 다음을 나타냅니다.
위의 두 관계를 조합하면 다음과 같습니다.
라디안과 그라디언 사이의 변환
{ 2 \ } 라디안은 1회전입니다.이것은 정의상 400 gon(400 gon 또는 400g g)의 그라디언입니다. 라디안에서 그라디언으로 하려면 {\ 그라디언에서 라디안으로 변환하려면 / 을 곱합니다.예를 들어 다음과 같습니다.
라디안 측정의 이점

미적분과 실용적인 기하학을 넘어선 수학의 대부분의 다른 분야들에서, 각도는 일반적으로 라디안으로 측정된다.이것은 라디안들이 수학적인 "자연성"을 가지고 있기 때문에 많은 중요한 결과들을 보다 우아하게 공식화 할 수 있다.
특히 삼각함수를 포함한 분석 결과는 함수의 인수가 라디안으로 표현될 때 우아하게 기술될 수 있다.예를 들어 라디안을 사용하면 단순 한계 공식으로 이어집니다.
이것은 수학에서 많은 다른 정체성의 기초이다.
이러한 특성 및 기타 특성으로 인해 삼각함수는 함수의 기하학적 의미와 명확하게 관련되지 않은 수학적 문제에 대한 해(예를 들어, 미분 d x -\ \{ { d^ 2}} - )에 대한 해, 평가에서 나타난다.적분 1 + , \ \ \ { { + x^ { } 등).그러한 모든 경우에, 함수에 대한 인수는 기하학적 맥락에서 각도의 라디안 측정에 대응하는 형태로 가장 자연스럽게 쓰여지는 것으로 밝혀졌다.
또한 삼각함수는 라디안을 사용할 때 단순하고 우아한 직렬 확장을 제공합니다.예를 들어 x가 라디안일 경우 sin x에 대한 Taylor 시리즈는 다음과 같습니다.
x가 도 단위로 표현되면 시리즈에는 θ/180의 거듭제곱을 포함하는 지저분한 요인이 포함됩니다. x가 도 수이면 라디안의 수는 y = µx / 180입니다.
비슷한 정신에서, 사인 및 코사인 함수와 지수 함수 사이의 수학적으로 중요한 관계는 함수의 인수가 라디안으로 되어 있을 때 우아하게 진술될 수 있다.
역사
각도의 정도에 반하는 라디안 측정의 개념은 일반적으로 1714년에 [8][9]로저 코테스에 의해 인정되었다.그는 이름을 제외한 모든 것에 라디안을 묘사했고, 자연스러움을 각도 측정 단위로 인식했다.라디안이라는 용어가 널리 퍼지기 전에는 이 단위를 일반적으로 [10]각도의 원형 측정이라고 불렀습니다.
호의 길이로 각도를 측정하는 아이디어는 이미 다른 수학자들에 의해 사용되고 있었다.예를 들어, 알-카시(c. 1400)는 직경 부품을 단위로 사용했는데, 여기서 직경 부품은 1/60 라디안이었다.그들은 또한 지름 [11]부분의 60진법 서브유닛을 사용했다.
레이디언이라는 용어는 1873년 6월 5일 벨파스트 퀸스 칼리지에서 제임스 톰슨(켈빈 경의 동생)이 낸 시험 문제에서 처음 출판되었다.1869년 세인트 앤드루스 대학의 토마스 뮤어가 rad, radial, radian이라는 용어 사이에서 망설였다.1874년, 제임스 톰슨과의 협의 후에 뮤어는 라디안을 [12][13][14]채택했다.그 후 한동안 라디안이라는 이름이 보편적으로 채택되지 않았다.Longmans' School Trigonometry는 [15]1890년에 발표되었을 때 여전히 라디안 원형 측도로 불렸다.
SI 단위로서의 이력
Paul Quincey 등이 쓰듯이, "국제 단위계(SI) 내의 각도의 상태는 오랫동안 논란과 [16]혼란의 원인이 되어왔다."1960년에 CGPM은 SI를 확립했고 라디안은 스테라디안과 함께 "보조 단위"로 분류되었다.CGPM이 라디안이 기본 단위인지 파생 [17]단위인지에 대한 결정을 내릴 수 없었기 때문에 이 특수 클래스는 공식적으로 "기본 단위 또는 파생 단위"로 간주되었다.리처드 넬슨은 "이러한 (보조 부대의 분류에 있어서의) 모호함은 그들의 적절한 [18]해석에 대한 활발한 논의를 불러일으켰다"고 쓰고 있다.1980년 5월 CCU(Consulticate Committee0 for Units)[19][20]는 상수 α = 1 rad를 사용하여 라디안을 SI 베이스 단위로 만드는 제안을 검토했으나 현재의 [20]관행에 대한 격변을 피하기 위해 이를 거부했다.
10월 1980년, 국제 도량형 총회는 보조 단위가 국제 도량형 총회나 표현에 SI그들을 사용하지 않고 그것을 사용하면서 생긴 자유 units,[18]전제 하에서 "[어떤 형식 주의]이 존재하는지에 파생된 허용 파생된 단위 차원도 있다고 결정했는데, 동시에 그리고 편리한 부분과 양 비행기 각도와 입체각이 일관성 있다고. migh기준량으로 간주되지 않는다." 및 "라디안과 스테라디안을 SI 기준 단위로 취급할 가능성은 7개 기준 [21]단위만을 기반으로 SI의 내부 일관성을 훼손한다."1995년에 국제 도량형 총회와"무차원 파생 유닛의 이름과 상징 표현에 다른 SI도출 단위에 따라 편리하다 사용할 수 있지만, 할 필요가 없다,"로 radian과 입체 호도 법에 대해 정의한 보조 단위의 수업을 물리쳤습니다.[22]. 주석인 MikhailKalinin이 2019년에 쓰기"근거 없는"로 말하기를, 1980년 국제 도량형 총회 결정 비난했다.1995년 CGPM의 결정에 일관되지 않은 주장이 사용되었고 "SI의 단어에 수많은 불일치, 불일치 및 모순"[23]이 도입되었다.
2013년 CCU 회의에서 Peter Mohr은 라디안을 기본 단위가 아닌 무차원 단위로 정의함으로써 발생하는 모순에 대해 발표했다.CCU의 Ian M. Mills 회장은 이것을 "엄청난 문제"라고 선언했고, SI의 각도 및 차원 없는 양에 관한 CCU 작업 그룹이 [24]설립되었습니다.CCU는 2021년에 [update]가장 최근에 만났지만 합의에 이르지 못했다.소수의 구성원들은 라디안이 기본 단위여야 한다고 강하게 주장했지만, 대다수는 현 상태가 용인되거나 변화가 해결할 수 있는 것보다 더 많은 문제를 야기할 것이라고 느꼈다.태스크 [25][26]그룹은 "SI 보충단위의 과거 사용을 검토하고 재도입이 유익한지 검토"하기 위해 설립되었다.
치수 분석
라디안은 θ = s/r로 정의됩니다. 여기서 θ는 라디안 단위의 하위 각도, s는 호 길이, r은 반지름입니다.1 라디안은 s=r인 각도에 해당하므로 1 라디안 = 1m/[27]m이다., r 는 표현에만 사용되며 일반적으로 길이의 [4]비율은 표현하지 않습니다.원형 섹터 θ = 2A/r의2 면적을 사용한 유사한 계산은 1 라디안을 1m2/[28]m로2 나타낸다.중요한 사실은 라디안이 1과 같은 무차원 단위라는 것입니다.SI 2019에서 라디안은 1 rad = [29]1로 정의된다.수학과 과학의 전 부문에 걸쳐에 있는 오랫동안 믿어져 온 연습 r의 사용 1993년 AAPT 물리적인 위원회 다른 각도 조치used,을 때만 다른 숫자 값은 그렇게 만들테니까는 radian 명시적으로 양에 나타납니다 지정한 d)1{\displaystyle \mathrm{rad}=1}.[30][31일]다. 예를 들어각도 측정량(rad), 각도 속도(rad/s), 각도 가속도(rad/s2) 및 비틀림 강성(nµm/rad)의 양이며 토크(Nµm) 및 각운동량(kgµm2/s)[32]의 양이 아니다.
Giacomo Frando는 "현 상황은 물리 방정식의 [33]차원 분석에서 불가피하게 유령이 나타나거나 사라지게 한다"고 말한다.예를 들어, 도르래에 끈으로 매달린 질량은 y=rµcm 상승 또는 하강합니다. 여기서 r은 도르래의 반지름(cm 단위), θ는 도르래가 회전하는 각도(라디안 단위)입니다.r에 θ를 곱하면 의 라디안 단위가 결과에서 사라집니다.마찬가지로 굴림 바퀴의 각속도 공식 θ=v/r에서 라디안은 [34]θ 단위로 나타나지만 오른쪽에는 나타나지 않는다.Anthony French는 이 현상을 "역학을 가르치는 데 있어 지속적인 문제"[35]라고 부른다.오버호퍼는 치수 해석 중에 라디안을 무시하고 관례와 문맥지식에 따라 단위로 라디안을 추가하거나 제거하는 전형적인 조언은 "학습적으로 만족스럽지 못하다"[36]고 말한다.
적어도 12명의 과학자들은 빠르면 1936년부터 [37][38][39]최근까지 라디안을 자체적인 "각도" 치수를 정의하는 기준 단위로 취급하자는 제안을 했다.Quincey의 제안서 검토는 두 가지 종류의 제안서를 요약한다.첫 번째 옵션은 반지름의 단위를 라디안당 미터로 변경하지만, 이는 원의 면적인 µr에2 대한 치수 분석과 호환되지 않습니다.다른 옵션은 치수 상수를 도입하는 것입니다.Quincey에 따르면 이 접근법은 SI에 비해 "논리적으로 엄격하지만" "많은 익숙한 수학 및 물리 [40]방정식의 수정"이 필요하다.
특히 Quincey는 Torrens의 제안을 식별하여 상수 [40]θ의0 도입과 유사한 방식으로 1 역 라디안(1 rad−1)과 동일한 상수 θ를 도입한다.이 변경으로 원의 중심에서 기울어진 각도에 대한 공식 s = rθ는 s = rθ로 수정되고 각도 θ의 사인(sine of angle)에 대한 Taylor 시리즈는 다음과 같이 됩니다.[39][41]
대문자 Sin {\은 각도의 차원으로 표현된 [41]단위와 무관한 "완전" 이며, 는 그 인수가 라디안으로 [42]가정된 순수 숫자에 대한 전통적인 함수입니다.한 형식이 [39][43]의미하는 것이 분명한 경우sin \operatorname은sin(\으로 표기할 수 있습니다.
SI는 방정식 θ = 1 또는 유사하게 1 rad = 1이 유지된다고 가정하는 자연 단위 시스템으로 이 프레임워크에 대해 상대적으로 고려될 수 있다.이 라디안 규약에서는 [20]수학 공식에서 in를 생략할 수 있다.
각도에 대한 치수 상수는 "좀 이상하다"며 치수 상수를 추가하기 위해 방정식을 수정하는 것이 어렵기 때문에 광범위한 사용을 [39]방해할 수 있습니다.라디안을 기본 단위로 정의하는 것은 긴 방정식의 단점이 [44]최소인 소프트웨어에 유용할 수 있습니다.예를 들어, Boost Units 라이브러리는 각도 단위를 다음과 같이 정의합니다.plane_angle디멘트를 클릭합니다.[45]매스매티카의 단위계는 각도를 각도 치수로 [46][47]간주한다.
물리에서의 사용
레이디언은 각도 측정이 필요할 때 물리학에서 널리 사용됩니다.예를 들어, 각 속도는 일반적으로 초당 라디안(rad/s)으로 측정됩니다.초당 1회 회전은 초당 2µ 라디안과 같습니다.
마찬가지로 각도 가속도는 종종 초당 라디안(rad/s2)으로 측정된다.
치수 해석을 위해 각속도와 각가속도의 단위는 각각 s와−2 s이다−1.
마찬가지로 두 파형의 위상차도 라디안으로 측정할 수 있습니다.예를 들어, 두 파형의 위상차가 (nπ2)) 라디안일 경우, 여기서 n은 정수이고, 두 파형의 위상차가 (n22 + + ),)이면, 그들은 역위상으로 간주됩니다.
SI 배수
서브멀티플의 메트릭프리픽스는 라디안과 함께 사용됩니다.밀리라디안(mrad)은 라디안의 1,000분의 1이고 마이크로라디안(μrad)은 라디안의 백만분의 1이다. 즉, 1 rad = 103 mrad = 106 μrad이다.
원에는 2µ × 1000 밀리라디안( 6 6283.185 밀리라디안)이 있다.그래서 1밀리애디안 은 원의 1/6283보다 약간 낮습니다.이 원의 "실제" 각도 측정 단위는 망원경 시력 제조업체가 망막의 (스타다메트릭) 거리 찾기를 사용하여 사용하고 있습니다.레이저 빔의 발산도 보통 밀리라디안 단위로 측정됩니다.
밀리라디안(0.001 rad)의 근사치는 NATO와 다른 군사 조직이 포격 및 표적에 사용합니다.각 밀은 원의 1/6400을 나타내며 밀리라디안보다 15/8% 또는 1.875% 작습니다.일반적으로 타겟팅 작업에서 볼 수 있는 작은 각도의 경우, 계산에 6400이라는 숫자를 사용하는 편리성이 작은 수학적 오류보다 중요합니다.과거 다른 포술 시스템은 스웨덴은 1/6300 스트럭을, 소련은 1/6000 스트럭을 사용하는 등 다른 근사치를 사용해 왔습니다.밀리라디안(milliradian)에 기초해 NATO 밀은 1000m 범위에서 약 1m에 근접한다(이렇게 작은 각도에서 곡률은 무시할 수 있다.
밀리보다 작은 접두사는 매우 작은 각도를 측정할 때 유용합니다.마이크로라디안(μrad)과 나노라디안(nrad)은 천문학에서 사용되며, 초저발광 레이저의 빔 품질 측정에도 사용할 수 있다.보다 일반적인 것은 648,000 rad(약 4.8481 마이크로라디안)의 아크초입니다.
「 」를 참조해 주세요.
메모들
레퍼런스
- ^ "Resolution 8 of the CGPM at its 20th Meeting (1995)". Bureau International des Poids et Mesures. Archived from the original on 2018-12-25. Retrieved 2014-09-23.
- ^ 국제측량국(International Bureau of Weights and Measures 2019, 페이지 151): "CGPM은 SI의 보조 단위, 즉 라디안과 스테라디안을 차원 없는 파생 단위로 해석하기로 결정했다."
- ^ Protter, Murray H.; Morrey, Charles B., Jr. (1970), College Calculus with Analytic Geometry (2nd ed.), Reading: Addison-Wesley, p. APP-4, LCCN 76087042
- ^ a b c 2019년 국제 도량형국, 페이지 151.
- ^ a b Weisstein, Eric W. "Radian". mathworld.wolfram.com. Retrieved 2020-08-31.
- ^ "ISO 80000-3:2006 Quantities and Units - Space and Time".
- ^ Hall, Arthur Graham; Frink, Fred Goodrich (January 1909). "Chapter VII. The General Angle [55] Signs and Limitations in Value. Exercise XV.". Written at Ann Arbor, Michigan, USA. Trigonometry. Vol. Part I: Plane Trigonometry. New York, USA: Henry Holt and Company / Norwood Press / J. S. Cushing Co. - Berwick & Smith Co., Norwood, Massachusetts, USA. p. 73. Retrieved 2017-08-12.
- ^ O'Connor, J. J.; Robertson, E. F. (February 2005). "Biography of Roger Cotes". The MacTutor History of Mathematics. Archived from the original on 2012-10-19. Retrieved 2006-04-21.
- ^ Roger Cotes는 1716년에 죽었다.1722년까지, 그의 사촌 로버트 스미스는 코테스의 수학적인 글을 모아 책 "하모니아 멘수라럼"에 발표했다. 스미스의 사설 논평의 한 장에서, 그는 처음으로 한 라디안의 가치를 도수로 제시한다.참조: Roger Cotes with Robert Smith, ed., Harmonia mensurarum... (Cambridge, 영국: 1722), 장:편집자 노테와 하모니암 멘수라룸, 95페이지 맨 위에 있습니다.95페이지부터: 180°는 단위 원(즉, θ 라디안)을 따라 θ(3.14159…)의 길이에 대응한다고 Smith는 쓴 후, "Une Modulus Canonis Trigonometrici prodibit 57.297795130 & c." (이때 삼각법 측정 단위 57.295.130도…)라고 쓴다.
- ^ 아이작 토드헌터, 평면 삼각법: College and School 사용(College and School, 페이지 10, Cambridge and London): MacMillan, 1864 OCLC 500022958
- ^ Luckey, Paul (1953) [Translation of 1424 book]. Siggel, A. (ed.). Der Lehrbrief über den kreisumfang von Gamshid b. Mas'ud al-Kasi [Treatise on the Circumference of al-Kashi]. Berlin: Akademie Verlag. p. 40.
- ^ Cajori, Florian (1929). History of Mathematical Notations. Vol. 2. Dover Publications. pp. 147–148. ISBN 0-486-67766-4.
- ^
- Muir, Thos. (1910). "The Term "Radian" in Trigonometry". Nature. 83 (2110): 156. Bibcode:1910Natur..83..156M. doi:10.1038/083156a0. S2CID 3958702.
- Thomson, James (1910). "The Term "Radian" in Trigonometry". Nature. 83 (2112): 217. Bibcode:1910Natur..83..217T. doi:10.1038/083217c0. S2CID 3980250.
- Muir, Thos. (1910). "The Term "Radian" in Trigonometry". Nature. 83 (2120): 459–460. Bibcode:1910Natur..83..459M. doi:10.1038/083459d0. S2CID 3971449.
- ^ Miller, Jeff (Nov 23, 2009). "Earliest Known Uses of Some of the Words of Mathematics". Retrieved Sep 30, 2011.
- ^ Frederick Sparks, Longmans School Trigonometry, 6페이지, 런던: Longmans, Green, Co, 1890 OCLC 877238863 (1891년판)
- ^ Quincey, Paul; Mohr, Peter J; Phillips, William D (1 August 2019). "Angles are inherently neither length ratios nor dimensionless". Metrologia. 56 (4): 043001. arXiv:1909.08389. Bibcode:2019Metro..56d3001Q. doi:10.1088/1681-7575/ab27d7. S2CID 198428043.
- ^ Le Système international d'unités (PDF) (in French), 1970, p. 12,
Pour quelques unités du Système International, la Conférence Générale n'a pas ou n'a pas encore décidé s'il s'agit d'unités de base ou bien d'unités dérivées.
[For some units of the SI, the CGPM still hasn't yet decided whether they are base units or derived units.] - ^ a b Nelson, Robert A. (March 1984). "The supplementary units". The Physics Teacher. 22 (3): 188–193. Bibcode:1984PhTea..22..188N. doi:10.1119/1.2341516.
- ^ Report of the 7th meeting (PDF) (in French), Consultative Committee for Units, May 1980, pp. 6–7
- ^ a b c 2021년 퀸시
- ^ 2019년 국제측량국, 페이지 174–175.
- ^ 2019년 국제 도량형 사무국, 페이지 179.
- ^ Kalinin, Mikhail I (1 December 2019). "On the status of plane and solid angles in the International System of Units (SI)". Metrologia. 56 (6): 065009. arXiv:1810.12057. Bibcode:2019Metro..56f5009K. doi:10.1088/1681-7575/ab3fbf. S2CID 53627142.
- ^ Consultative Committee for Units (11–12 June 2013). Report of the 21st meeting to the International Committee for Weights and Measures (Report). pp. 18–20.
- ^ Consultative Committee for Units (21–23 September 2021). Report of the 25th meeting to the International Committee for Weights and Measures (Report). pp. 16–17.
- ^ "CCU Task Group on angle and dimensionless quantities in the SI Brochure (CCU-TG-ADQSIB)". BIPM. Retrieved 26 June 2022.
- ^ 2019년 국제측량국 페이지 151: "1 라디안은 s = r"의 각도에 해당한다.
- ^ Quincey 2016, 페이지 844: "또한 Mohr & Phillips 2015에서 언급한 바와 같이 라디안은 섹터의 면적 A(A = 1/2 µr2)로 정의할 수 있으며, 이 경우 단위2 mµm를−2 갖는다."
- ^ 2019년 국제측량국 페이지 151: "1 라디안은 s = r인 각도에 해당하므로 1 rad = 1"
- ^ 2019년 국제 도량형국, 페이지 137.
- ^ Bridgman, Percy Williams (1922). Dimensional analysis. New Haven : Yale University Press.
Angular amplitude of swing [...] No dimensions.
- ^ Aubrecht, Gordon J.; French, Anthony P.; Iona, Mario; Welch, Daniel W. (February 1993). "The radian—That troublesome unit". The Physics Teacher. 31 (2): 84–87. Bibcode:1993PhTea..31...84A. doi:10.1119/1.2343667.
- ^ Prando, Giacomo (August 2020). "A spectral unit". Nature Physics. 16 (8): 888. Bibcode:2020NatPh..16..888P. doi:10.1038/s41567-020-0997-3. S2CID 225445454.
- ^ Leonard, William J. (1999). Minds-on Physics: Advanced topics in mechanics. Kendall Hunt. p. 262. ISBN 978-0-7872-5412-4.
- ^ French, Anthony P. (May 1992). "What happens to the 'radians'? (comment)". The Physics Teacher. 30 (5): 260–261. doi:10.1119/1.2343535.
- ^ Oberhofer, E. S. (March 1992). "What happens to the 'radians'?". The Physics Teacher. 30 (3): 170–171. Bibcode:1992PhTea..30..170O. doi:10.1119/1.2343500.
- ^ 브린스메이드 1936; 로맹 1962; 에더 1982; 토렌스 1986; 브라운스타인 1997; 레비-레블론드 1998; 포스터 2010; 밀스 2016; 퀸시 2021; 레오나드 2021; 모어 외 2022.
- ^ Mohr & Phillips 2015.
- ^ a b c d Quincey, Paul; Brown, Richard J C (1 June 2016). "Implications of adopting plane angle as a base quantity in the SI". Metrologia. 53 (3): 998–1002. arXiv:1604.02373. Bibcode:2016Metro..53..998Q. doi:10.1088/0026-1394/53/3/998. S2CID 119294905.
- ^ a b 무성의한 2016년.
- ^ a b 토렌스 1986.
- ^ Mohr et al. 2022, 페이지 6
- ^ Mohr et al. 2022, 페이지 8-9.
- ^ Quincey, Paul; Brown, Richard J C (1 August 2017). "A clearer approach for defining unit systems". Metrologia. 54 (4): 454–460. arXiv:1705.03765. Bibcode:2017Metro..54..454Q. doi:10.1088/1681-7575/aa7160. S2CID 119418270.
- ^ Schabel, Matthias C.; Watanabe, Steven. "Boost.Units FAQ - 1.79.0". www.boost.org. Retrieved 5 May 2022.
Angles are treated as units
- ^ Mohr et al. 2022, 3페이지
- ^ "UnityDimensions—Wolfram Language Documentation". reference.wolfram.com. Retrieved 1 July 2022.
- International Bureau of Weights and Measures (20 May 2019), The International System of Units (SI) (PDF) (9th ed.), ISBN 978-92-822-2272-0, archived (PDF) from the original on 8 May 2021
- Brinsmade, J. B. (December 1936). "Plane and Solid Angles. Their Pedagogic Value When Introduced Explicitly". American Journal of Physics. 4 (4): 175–179. Bibcode:1936AmJPh...4..175B. doi:10.1119/1.1999110.
- Romain, Jacques E. (July 1962). "Angle as a fourth fundamental quantity". Journal of Research of the National Bureau of Standards, Section B. 66B (3): 97. doi:10.6028/jres.066B.012.
- Eder, W E (January 1982). "A Viewpoint on the Quantity "Plane Angle"". Metrologia. 18 (1): 1–12. Bibcode:1982Metro..18....1E. doi:10.1088/0026-1394/18/1/002.
- Torrens, A B (1 January 1986). "On Angles and Angular Quantities". Metrologia. 22 (1): 1–7. Bibcode:1986Metro..22....1T. doi:10.1088/0026-1394/22/1/002.
- Brownstein, K. R. (July 1997). "Angles—Let's treat them squarely". American Journal of Physics. 65 (7): 605–614. Bibcode:1997AmJPh..65..605B. doi:10.1119/1.18616.
- Lévy-Leblond, Jean-Marc (September 1998). "Dimensional angles and universal constants". American Journal of Physics. 66 (9): 814–815. Bibcode:1998AmJPh..66..814L. doi:10.1119/1.18964.
- Foster, Marcus P (1 December 2010). "The next 50 years of the SI: a review of the opportunities for the e-Science age". Metrologia. 47 (6): R41–R51. doi:10.1088/0026-1394/47/6/R01.
- Mohr, Peter J; Phillips, William D (1 February 2015). "Dimensionless units in the SI". Metrologia. 52 (1): 40–47. arXiv:1409.2794. Bibcode:2015Metro..52...40M. doi:10.1088/0026-1394/52/1/40.
- Quincey, Paul (1 April 2016). "The range of options for handling plane angle and solid angle within a system of units". Metrologia. 53 (2): 840–845. Bibcode:2016Metro..53..840Q. doi:10.1088/0026-1394/53/2/840.
- Mills, Ian (1 June 2016). "On the units radian and cycle for the quantity plane angle". Metrologia. 53 (3): 991–997. Bibcode:2016Metro..53..991M. doi:10.1088/0026-1394/53/3/991.
- Quincey, Paul (1 October 2021). "Angles in the SI: a detailed proposal for solving the problem". Metrologia. 58 (5): 053002. arXiv:2108.05704. Bibcode:2021Metro..58e3002Q. doi:10.1088/1681-7575/ac023f. S2CID 236547235.
- Leonard, B P (1 October 2021). "Proposal for the dimensionally consistent treatment of angle and solid angle by the International System of Units (SI)". Metrologia. 58 (5): 052001. Bibcode:2021Metro..58e2001L. doi:10.1088/1681-7575/abe0fc. S2CID 234036217.
- Mohr, Peter J; Shirley, Eric L; Phillips, William D; Trott, Michael (23 June 2022). "On the dimension of angles and their units". Metrologia. arXiv:2203.12392. doi:10.1088/1681-7575/ac7bc2.
외부 링크
 Wikimedia Commons의 Radian 관련 미디어
Wikimedia Commons의 Radian 관련 미디어
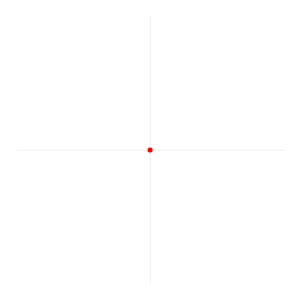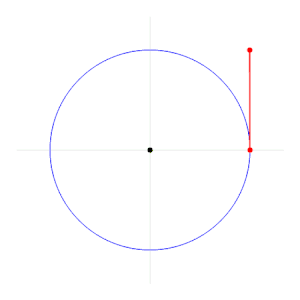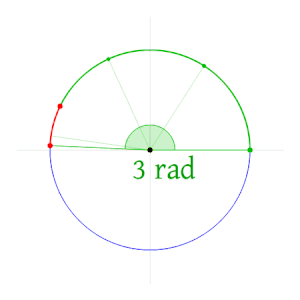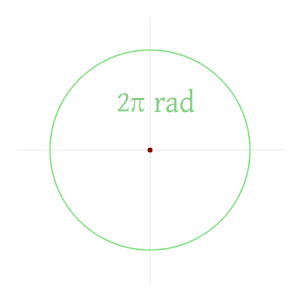
















 필요하기 때문에]
필요하기 때문에]


















 각도의 차원으로 표현된
각도의 차원으로 표현된  그 인수가 라디안으로
그 인수가 라디안으로  표기할 수 있습니다.
표기할 수 있습니다.