내각
Inscribed angle기하학에서, 새겨진 각도는 두 개의 화음이 원 위에서 교차할 때 원의 내부에 형성된 각이다. 또한 원의 한 점에서 두 개의 주어진 점에 의해 그 원 위의 한 점에서 하위되는 각도로 정의할 수 있다.
마찬가지로, 새겨진 각도는 끝점을 공유하는 원의 두 개의 화음으로 정의된다.
새긴 각도 정리(Star Trek Leemma라고도[citation needed] 한다)는 같은 호를 소계하는 중심 각도와 새긴 각도의 측도를 연관시킨다.
새겨진 각도 정리는 유클리드 원소 제3권에 발의안 제20호로 나타난다.
정리
성명서
새겨진 각도 정리는 원 안에 새겨진 각 θ이 원 위에서 같은 호를 미는 중심각 2θ의 절반이라고 명시하고 있다. 따라서 원의 정점이 원의 다른 위치로 이동될 때 각도는 변하지 않는다.
증명
하나의 화음이 직경인 경우 새겨진 각도
오른쪽의 도표에서처럼 오를 원의 중심이 되게 하라. 원 위의 두 점을 선택하고 V와 A라고 부른다. 선 VO를 그리고 O를 지나 점 V와 정반대인 점 B에서 원을 교차하도록 확장한다. 정점이 점 V이고 면이 점 A와 B를 통과하는 각도를 그린다.
OA선을 그어라. 앵글 BOA는 중심각이다; 그것을 θ이라고 부른다. 선 OV와 OA는 둘 다 원의 반지름이기 때문에 길이가 같다. 따라서 삼각형 VOA는 등각이기 때문에 각 BVA(내각)와 각 VAO가 같으므로 각각을 ψ으로 표시하도록 한다.
앵글 BOA와 AOV는 O를 통과하는 라인 VB가 직선이기 때문에 최대 180°까지 더해진다. 따라서 각도 AOV는 180° - -을 측정한다.
삼각형의 세 각도가 최대 180°에 이르는 것으로 알려져 있으며, 삼각형 VOA의 세 각도는 다음과 같다.
- 180° − θ
- ψ
- ψ.
그러므로
빼다
양쪽으로부터,
여기서 θ은 중심각 중첩 호 AB이고 ψ은 내각 중첩 호 AB이다.
내부 원 중심에 새겨진 각도
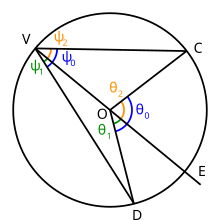
중심점이 O점인 원을 지정하면 원의 V, C, D점 3개를 선택하십시오. 그리기 선 VC 및 VD: 각도 DVC는 내각이다. 이제 선 VO를 그리고 점 O를 지나 연장하여 점 E에서 원과 교차하도록 한다. 각도 DVC는 원의 호 DC를 하위화한다.
이 호 안에 점 E를 포함한다고 가정합시다. 점 E는 점 V와 정반대다. 각도 DVE와 EVC도 각도가 새겨져 있지만, 이 두 각도 모두 원의 중심을 통과하는 한 면을 가지고 있기 때문에 위의 1부로부터의 정리를 적용할 수 있다.
그러므로
그럼 그렇게 합시다.
하도록
OC 및 OD 라인을 그리십시오. 각도 DOC는 중심 각도지만 각도 DOE와 EOC도 마찬가지다.
내버려두다
하도록
1부에서 우리는 =2 1 }, 2 2 이러한 결과를 방정식 (2) 산출량과 결합하여 알 수 있다.
따라서 등식 (1)에 의해
외관에 원의 중심이 새겨진 각도
이전의 사례를 확장하여 이 증명의 첫 부분에서 논의한 바와 같이, 새겨진 각도의 측정치가 두 개의 새겨진 각도의 차이인 경우를 다룰 수 있다.
중심점이 O점인 원을 지정하면 원의 V, C, D점 3개를 선택하십시오. 그리기 선 VC 및 VD: 각도 DVC는 내각이다. 이제 선 VO를 그리고 점 O를 지나 연장하여 점 E에서 원과 교차하도록 한다. 각도 DVC는 원의 호 DC를 하위화한다.
이 호에는 점 E가 포함되지 않는다고 가정합시다. 점 E는 점 V와 정반대다. 앵글 EVD와 EVC도 새겨지지만, 이 두 앵글은 모두 원의 중심을 통과하는 한 쪽을 가지고 있기 때문에, 위의 제1부로부터의 정리를 그들에게 적용할 수 있다.
그러므로
- C= E C - E .
그럼 그렇게 합시다.
하도록
OC 및 OD 라인을 그리십시오. 각도 DOC는 중심 각도지만 각도 EOD와 EOC도 마찬가지다.
내버려두다
하도록
1부에서 우리는 =2 1 }, 2 이러한 결과를 방정식 (4) 산출량과 결합하여 알 수 있다.
따라서 등식 (3)에 의해
코롤라리
유사한 인수에 의해, 교차점 중 하나에서 현과 접선 사이의 각도는 현에 의해 하위화된 중심 각도의 절반과 같다. 원의 접선도 참조하십시오.
적용들
새겨진 각도 정리는 평면의 기본적인 유클리드 기하학의 많은 증거에 사용된다. 그 정리의 특별한 경우는 탈레스의 정리인데, 직경으로 미분하는 각도는 항상 90°, 즉 직각이라고 한다. 정리의 결과, 주기적 4차측정의 반대 각도는 180°에 이른다. 반대로, 이것이 사실인 모든 4각형은 원 안에 새겨질 수 있다. 또 다른 예로서, 새겨진 각도 정리는 원에 관한 점의 힘과 관련된 몇 가지 이론의 기초가 된다. 또한, 그것은 두 개의 화음이 원을 그리며 교차할 때, 그들 조각의 길이의 생산물이 동일하다는 것을 증명할 수 있게 해준다.
타원, 하이퍼볼라 및 파라볼라에 대한 내각각 정리
타원, 하이퍼볼라, 파라볼라에도 내각 이론이 존재한다. 본질적인 차이는 각도의 측정이다. (각도는 한 쌍의 교차선으로 간주된다.)
참조
- Ogilvy, C. S. (1990). Excursions in Geometry. Dover. pp. 17–23. ISBN 0-486-26530-7.
- Gellert W, Küstner H, Hellwich M, Kästner H (1977). The VNR Concise Encyclopedia of Mathematics. New York: Van Nostrand Reinhold. p. 172. ISBN 0-442-22646-2.
- Moise, Edwin E. (1974). Elementary Geometry from an Advanced Standpoint (2nd ed.). Reading: Addison-Wesley. pp. 192–197. ISBN 0-201-04793-4.
외부 링크
- Weisstein, Eric W. "Inscribed Angle". MathWorld.
- 중심각과 내각의 관계
- 잘린 각도에서 우적우적 씹기
- 아크 중앙 각도(대화형 애니메이션 포함)
- 대화형 애니메이션을 사용한 호 주변(구독) 각도
- 대화형 애니메이션을 사용한 아크 중앙 각도 정리
- bookofproofs.org에서 확인하십시오.