콘코이드(수학)

콘코이드(conchoid)는 고정점 O, 다른 곡선, 길이 d에서 파생된 곡선이다. 고대 그리스의 수학자 니코메데스에 의해 발명되었다.^[1]

설명

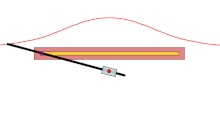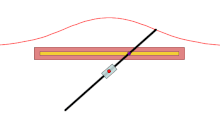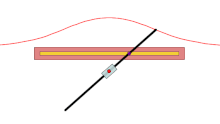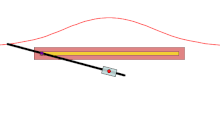
A에서 주어진 곡선을 교차하는 모든 선에서 O를 통과하는 모든 선에 대해 A에서 d인 선 위의 두 점은 콘코이드에 있다. 따라서 콘코이드는 주어진 곡선의 시소이드와 반지름 d와 중심 O의 원이다. 그들은 겉가지 모양이 소라껍질을 닮았기 때문에 소라로 불린다.

가장 간단한 표현은 원점에 O가 있는 극좌표를 사용한다. 만약

$(\displaystyle r=\disput (\theta )}$

그러면 주어진 곡선을 표현한다.

$(\displaystyle r=\pm(\theta )\pm d}$

콘코이드를 표현한다.

곡선이 선이라면, 콘코이드는 니코메데스의 콘코이드다.

예를 들어, 곡선이 선 $x{\displaystyle }$= ${\displaystyle x=a$인 경우 선의 극성 형태는 r${\displaystyle }$= ${\displaystyle 초a}$ ${\displaystyle \theta }$ θ$${\$displaystyle r=a\sec \theta }$이며 따라서$$ 콘코이드는 다음과 같이 파라메트릭적으로 표현될 수 있다.

$\displaystyle x=a\pm d\cos \theta,\,y=an\tan \theta \pm d\sin \theta.}$

리마콘은 주어진 곡선으로 원을 이룬 콘코이드다.

이른바 드 슬루제의 콘코이드와 뒤러의 콘코이드는 실제로 콘코이드가 아니다. 전자는 엄격한 시스소이드고 후자는 아직 더 일반적인 공사다.

참고 항목

• 시스소이드
• 스트롭호이드

참조

• J. Dennis Lawrence (1972). A catalog of special plane curves. Dover Publications. pp. 36, 49–51, 113, 137. ISBN 0-486-60288-5.

외부 링크

위키미디어 공용 콘코이드 관련 매체