확률 과정
Stochastic process| 통계에 관한 시리즈의 일부 |
| 확률론 |
|---|
 |
확률론 및 관련 분야에서 확률적(/stoʊkkéstkk/) 또는 랜덤 프로세스는 일반적으로 랜덤 변수 패밀리로 정의되는 수학적 객체이다.확률적 과정은 랜덤하게 변화하는 것으로 보이는 시스템 및 현상의 수학적 모델로 널리 사용된다.예를 들어 세균 인구의 증가, 열 잡음으로 인한 전류 변동, 가스 [1][4][5]분자의 이동 등이 있습니다.확률적 과정은 생물학,[6] 화학,[7] 생태학,[8] 신경과학,[9] 물리,[10] 이미지 처리, 신호 처리,[11] 제어 이론,[12] 정보 이론,[13] 컴퓨터 과학,[14] 암호학[15] 및 [16]통신과 같은 많은 분야에서 응용된다.게다가 금융시장의 무작위적인 변화는 [17][18][19]금융에서 확률적 과정을 광범위하게 사용하는 동기가 되었다.
응용과 현상에 대한 연구는 차례로 새로운 확률적 과정의 제안에 영감을 주었다.그러한 확률적 과정의 예로는 루이 바첼리에가 파리 [22]증시의 가격 변화를 연구하기 위해 사용한 Wiener 과정 또는 Brownian 움직임 [a]과정과 A. K. Erlang이 특정 [23]기간 동안 발생한 전화의 수를 연구하기 위해 사용한 Poisson 과정이 있다.이 두 확률적 과정은 확률적 [1][4][24]과정 이론에서 가장 중요하고 중심적인 것으로 간주되며, 다른 환경과 [22][25]국가에서 바첼리에와 에를랑의 전후 모두에서 반복적이고 독립적으로 발견되었다.
확률적 과정은 [28][29]함수 공간에서 랜덤 요소로 해석될 수 있기 때문에 랜덤 함수라는 용어는 확률적 [26][27]또는 랜덤 프로세스를 참조하기 위해서도 사용됩니다.확률적 과정과 랜덤 과정이라는 용어는 종종 [28][30]랜덤 변수를 색인화하는 집합에 대한 특정 수학적 공간이 없이 서로 바꿔서 사용됩니다.그러나 종종 이 두 항은 랜덤 변수가 [5][30]실제 선의 정수 또는 구간에 의해 색인화될 때 사용됩니다.랜덤 변수가 데카르트 평면이나 일부 고차원 유클리드 공간에 의해 색인화된다면,[5][31] 랜덤 변수의 집합은 보통 랜덤 필드라고 불립니다.확률 과정의 값은 항상 숫자가 아니며 벡터나 다른 수학적 [5][29]객체일 수 있습니다.
확률적 프로세스는 수학적 특성에 따라 [32]랜덤 워크,[33] 마르코프 프로세스,[34] 레비 프로세스,[35][36] 가우스 프로세스, [37]랜덤 필드, 갱신 프로세스 및 [38]분기 프로세스를 포함한 다양한 범주로 그룹화할 수 있습니다.확률적 과정 연구는 확률, 미적분, 선형 대수, 집합론, 위상뿐만[39][40][41] 아니라 실제 해석, 측정 이론, 푸리에 분석, 함수 [42][43][44]분석과 같은 수학적 분석의 분파로부터 수학적 지식과 기술을 사용한다.확률적 과정 이론은 수학에[45] 중요한 공헌으로 간주되며 이론적인 이유와 응용 [46][47][48]둘 다에서 활발한 연구 주제가 되고 있다.
서론
확률적 또는 랜덤 프로세스는 어떤 수학적 집합에 의해 색인화된 랜덤 변수의 집합으로 정의될 수 있으며, 이는 확률적 프로세스의 각 랜덤 변수가 집합 [4][5]내의 요소와 고유하게 연관되어 있음을 의미합니다.랜덤 변수의 인덱스에 사용되는 세트를 인덱스 세트라고 합니다.역사적으로, 지수 집합은 자연수와 같은 실선의 일부 부분 집합이었고,[1] 지수 집합은 시간에 대한 해석을 제공한다.집합의 각 랜덤 변수는 상태 공간이라고 하는 동일한 수학적 공간의 값을 취합니다.이 상태 공간은 예를 들어 정수, 실선 nn-차원 유클리드 [1][5]공간일 수 있습니다.증분은 확률적 프로세스가 두 지수 값 사이에서 변화하는 양으로, 종종 [49][50]두 시점으로 해석됩니다.확률적 과정은 그 무작위성으로 인해 많은 결과를 가질 수 있으며, 확률적 과정의 단일 결과를 다른 이름 중에서 샘플 함수 또는 실현이라고 [29][51]한다.
분류
확률 프로세스는 상태 공간, 지수 세트 또는 랜덤 변수 간의 의존성 등 다양한 방법으로 분류할 수 있다.일반적인 분류 방법 중 하나는 인덱스 세트와 상태 공간의 [52][53][54]카디널리티에 의한 분류입니다.
확률적 과정의 지수 집합이 유한한 수의 수, 정수 집합 또는 자연수와 같은 유한하거나 셀 수 있는 수의 요소를 갖는 경우 확률적 과정은 이산적 [55][56]시간이라고 한다.인덱스 세트가 실제 행의 간격일 경우 시간은 연속이라고 합니다.두 가지 유형의 확률 프로세스를 각각 이산 시간과 연속 시간 확률 [49][57][58]과정이라고 한다.이산 시간 확률 프로세스는 특히 지수 집합이 [59][60]셀 수 없기 때문에 연속 시간 프로세스는 보다 진보된 수학적 기술과 지식을 필요로 하기 때문에 연구하기 더 쉬운 것으로 간주된다.지수 집합이 정수 또는 일부 부분 집합인 경우 확률적 과정은 랜덤 시퀀스라고도 [56]할 수 있습니다.
상태 공간이 정수 또는 자연수일 경우 확률 과정은 이산 또는 정수 확률 과정이라고 불립니다.상태 공간이 실선일 경우, 확률적 과정은 실값 확률 과정 또는 연속적인 상태 공간을 갖는 과정이라고 한다.상태 공간이 n차원 유클리드 공간인 경우 확률 프로세스는 n}차원 벡터 프로세스 nn}-벡터 [52][53]프로세스라고 합니다.
어원학
영어에서 확률적이라는 단어는 원래 "추측에 관계하다"라는 정의와 함께 형용사로 사용되었고 "표적을 겨냥하다, 추측하다"라는 뜻의 그리스어에서 유래했으며, 옥스포드 영어 사전에는 1662년이 가장 이른 시기로 [61]나와 있다.1713년 라틴어로 출판된 확률 아르스 추측디(Ars Expectandi)에 관한 그의 연구에서 야콥 베르누이는 "Ars Expectandi sive Scoutastice"라는 문구를 사용했는데, 이는 "추측 또는 확률학의 기술"[62]로 번역되었다.이 문구는 1917년 무작위라는 의미의 확률적 단어를 독일어로 쓴 Ladislaus Bortkiewicz에[63] 의해 Bernouli와 관련하여 사용되었다.확률 과정이라는 용어는 1934년 조셉 [61]두브의 논문에서 영어로 처음 등장했다.이 용어와 특정한 수학적 정의를 위해, Doob은 확률자 프로제라는 용어가 독일어로 사용된 1934년의 또 다른 논문을 인용했다.[64][65] 비록 독일어 용어가 [66]1931년 안드레이 콜모고로프에 의해 일찍이 사용되었음에도 불구하고 말이다.
옥스포드 영어사전에 따르면, 우연이나 행운과 관련된 영어에서 무작위라는 단어의 초기 발생은 16세기로 거슬러 올라가는 반면, 이전의 기록된 용법은 14세기에 "충분함, 엄청난 속도, 힘, 또는 폭력"을 의미하는 명사로 시작되었다.그 단어 자체는 "속도, 서두름"을 뜻하는 중세 프랑스어 단어에서 유래했으며, 아마도 "달리다" 또는 "달리다"를 의미하는 프랑스어 동사에서 유래했을 것이다.무작위 과정이라는 용어의 첫 번째 서면 출현은 옥스퍼드 영어 사전이 동의어로 제공하는 확률 과정보다 앞서며,[67] 1888년 프란시스 에지워스가 발표한 기사에 사용되었다.
용어.
확률적 과정의 정의는 [68]다양하지만, 확률적 과정은 전통적으로 일부 [69][70]집합에 의해 색인화된 랜덤 변수의 집합으로 정의된다.무작위 과정과 확률 과정이라는 용어는 동의어로 간주되며, 지수 집합이 정확하게 [28][30][31][71][72][73]지정되지 않은 상태에서 상호 교환적으로 사용됩니다."collection"[29][71] 또는 "family"가 모두 사용되는[4][74] 반면 "index set" 대신 "parameter [29]set" 또는 "parameter [31]space"라는 용어가 사용되는 경우도 있습니다.
랜덤 함수라는 용어는 확률적 또는 랜덤 프로세스를 [5][75][76]참조하기 위해 사용되기도 하지만, 확률적 프로세스가 실제 [29][74]값을 취할 때만 사용되기도 합니다.이 용어는 또한 지수세트 수학적 공간은 진짜 line,[5][77]보다 다른 때 인덱스 설정 해석되고 다른 time,[5][77][78]조건이 지수 세트 랜덤 필드 같은 사용되는 동안 조건을 통계적 과정과 무작위 과정은 보통 사용되다 n{n\displaystyle}-dimensional 유클리드 공간 사용된다. Rn{)^{ or 다지관.[5][29][31]
표기법
한 통계적 과정, 다른 방법 중{X(t)}지 ∈ T{\displaystyle\와 같이{X(t)\}_{Tt\in}},[57]{Xt}t∈ T{\displaystyle\와 같이{X_{t}\}_{Tt\in}에 의해}{Xt}{\displaystyle\와 같이{X_{t}\ ,[70]}}[79]{X(t)}{\displaystyle\와 같이{X(t)\}}또는 단순히로 X{X\displaystyle}또는 X(t)표시될 수 있다. {\displaysty X 단, X는 함수 [80]표기법의 오용으로 간주됩니다.예를 들어 X( ){ X t{는 확률 [79]프로세스 전체가 아니라 t { t의 랜덤 변수를 참조하기 위해 사용됩니다.인덱스 세트가 T [ , ] { T = [ , \ }인 경우, 확률적 [30]과정을 나타내기 ( , 0) { ( _ { t , t , t \ 0 ) 라고쓸 수 있습니다.
예
베르누이 과정
가장 단순한 확률 과정 중 하나는 베르누이 프로세스로,[81] 독립적이고 균등하게 분포된 (iid) 랜덤 변수의 시퀀스이다. 각 랜덤 변수는 1 또는 0(: 확률p {\p}, 1 - {\의 값을 취한다.이 과정은 코인을 반복적으로 던지는 것으로 연결될 수 있습니다. 코인의 헤드를 얻을 확률은 p이고 값은 1이고 꼬리 값은 [82]0입니다.즉, 베르누이 과정은 iid Bernouli 랜덤 [83]변수의 연속이며, 여기서 동전 던지기는 베르누이 [84]시행의 한 예입니다.
랜덤 워크
랜덤 워크는 보통 유클리드 공간에서 iid 랜덤 변수 또는 랜덤 벡터의 합으로 정의되는 확률적 과정이기 때문에 이산 [85][86][87][88][89]시간에 변화하는 과정이다.그러나 일부에서는 연속적으로 [90]변화하는 과정, 특히 금융에서 사용되는 위너 과정을 지칭하는 용어로도 사용되는데, 이로 인해 혼란이 생겨 [91]비판의 대상이 되고 있다.그 밖에 다양한 유형의 랜덤 워크가 있으며, 그 상태 공간이 격자나 그룹과 같은 다른 수학적 객체가 될 수 있도록 정의되어 있으며, 일반적으로 고도로 연구되고 다양한 [90][92]분야에서 많은 응용 분야를 가지고 있다.
랜덤 워크의 전형적인 예는 단순 랜덤 워크로 알려져 있는데, 이는 정수를 상태 공간으로 하는 이산 시간에서의 확률 과정이며, 베르누이 프로세스에 기초하고 있으며, 베르누이 변수는 각각 양의 값 또는 음의 값을 취한다.즉, 단순 랜덤 워크는 정수에 대해 발생하며, 그 값은 확률: p\ p에 따라 1씩 증가하거나 1 -\ 1-p에 따라 1만큼 감소하므로 이 랜덤 워크의 인덱스 세트는 자연수이고 상태 공간은 정수이다. 5 { p5인 경우, 이 랜덤 워크를 대칭 랜덤 [93][94]워크라고 합니다.
위너법
위너 프로세스는 정상적이고 독립적인 증분을 갖는 확률적 과정으로 [2][95]증분의 크기에 따라 정규적으로 분포됩니다.위너 과정은 수학적인 존재를 증명한 노버트 위너(Norbert Wiener)의 이름을 따 명명됐지만 [96][97][98]이 과정은 액체의 브라운 운동 모델로서의 역사적 연관성 때문에 브라운 운동 과정 또는 브라운 운동으로도 불린다.
확률 이론에서 중심적인 역할을 하는 위너 과정은 종종 가장 중요하고 연구된 확률 과정으로 여겨지며, 다른 확률 [1][2][3][99][100][101][102]과정과의 연관성을 가지고 있다.지수 집합과 상태 공간은 각각 음수가 아닌 숫자와 실수이므로 연속 지수 집합과 상태 [103]공간을 모두 갖습니다.그러나 프로세스를 보다 일반적으로 정의할 수 있으므로 상태 공간은 n n차원 유클리드 [92][100][104]이 될 수 있습니다.어떤 증분의 평균이 0일 경우, 그 결과 발생하는 위너 또는 브라운 운동 과정은 드리프트가 0이라고 합니다.임의의 2개 시점의 증분의 평균이 일정μ실수에 시간차를 곱한 것과 같을 경우, 그 결과 발생하는 확률적 은 드리프트displaystyle \mu[105][106][107]를 갖는다고 합니다.
Wiener 공정의 샘플 경로는 거의 확실히 어디에서나 연속적이지만 다른 점은 없습니다.단순 랜덤 [50][106]워크의 연속 버전으로 간주할 수 있다.이 과정은 특정 랜덤 워크와 같은 다른 확률적 과정의 수학적 한계가 [108][109]축소될 때 발생하는데, 이것은 도스커의 정리 또는 불변성 원리의 주제이며, 함수 중심 한계 [110][111][112]정리라고도 알려져 있다.
위너 프로세스는 마르코프 과정, 레비 과정 및 가우스 [2][50]과정을 포함한 확률적 과정의 중요한 계열의 구성원이다.이 과정은 또한 많은 응용 분야를 가지고 있으며 확률적 [113][114]미적분에 사용되는 주요 확률적 과정이다.예를 들어 블랙-숄즈-머튼 [117]모델에서 사용되는 양적 [115][116]금융에서 중심적인 역할을 한다.이 과정은 또한 다양한 무작위 [3][118][119]현상에 대한 수학적 모델로서 사회과학의 일부 분과뿐만 아니라 대부분의 자연과학 분야를 포함한 다양한 분야에서 사용된다.
포아송 과정
포아송 과정은 형태와 정의가 [120][121]다른 확률적 과정입니다.이것은 계수 과정으로 정의될 수 있는데, 이것은 일정 시간까지 점이나 사건의 랜덤 수를 나타내는 확률 과정이다.0부터 지정된 시간까지의 구간에 있는 공정의 점 수는 해당 시간과 일부 모수에 따라 달라지는 포아송 랜덤 변수입니다.이 과정은 자연수를 상태 공간으로 하고 음수가 아닌 숫자를 지수 집합으로 합니다.이 공정은 계수 [120]공정의 예로 해석될 수 있기 때문에 포아송 계수 공정이라고도 합니다.
포아송 공정이 단일 양의 상수로 정의되어 있으면 이 공정을 동종 포아송 [120][122]공정이라고 합니다.동종 포아송 과정은 마르코프 과정과 레비 [50]과정과 같은 확률적 과정의 중요한 클래스의 구성원이다.
동종 포아송 공정은 다양한 방법으로 정의 및 일반화할 수 있습니다.지수 집합이 실선이 되도록 정의할 수 있으며, 이 확률적 과정을 정지 포아송 [123][124]과정이라고도 합니다.Poisson 공정의 파라미터 상수를 t\의음이 아닌 적분 가능 함수로 대체하면 결과 공정을 비균질 또는 비균질 포아송 공정이라고 하며, 공정의 점의 평균 밀도가 더 이상 [125]일정하지 않습니다.큐잉 이론의 기본 프로세스로서, 포아송 프로세스는 수학 모델을 위한 중요한 프로세스로, 특정 시간 창에서 [126][127]무작위로 발생하는 사건의 모델에 대한 응용 프로그램을 찾습니다.
실제 선에 정의되어 있는 포아송 프로세스는 확률적 [50][128]과정으로 해석될 수 있으며, 특히 랜덤 [129][130]객체입니다.그러나 n n 유클리드 공간 또는 기타 수학적 [131]공간에 정의할 수 있으며, 확률적 [129][130]과정이 아닌 랜덤 집합 또는 랜덤 계수 측도로 해석되는 경우가 많다.이 설정에서는 포아송 점 공정이라고도 하는 포아송 공정이 적용 및 이론적 [23][132]이유로 확률 이론에서 가장 중요한 개체 중 하나입니다.그러나 푸아송 과정은 종종 다른 [132][133]수학적 공간이 아닌 실선상으로만 고려되기 때문에 필요한 만큼의 관심을 받지 못한다고 언급되어 왔다.
정의들
확률 과정
확률적 프로세스는 공통 확률 공간 P에 정의된 랜덤 변수 집합(\ 으로 정의되며, 여기서\ \ 는 표본 공간, 는 \스타일이다P는 확률 측도입니다.랜덤 변수는 일부 T T에 의해 색인화되어 모두 동일한 수학 S {\ S의 값을 갖습니다.이 값은 \} - algebra Sigma[29]에 대해 측정할 수 있어야 합니다.
즉, 확률공간 { {\ 및 측정가능공간 {에 대해 확률적 프로세스는 다음과 같이 [81]쓸 수 있는 S{\S-value}의 집합이다.
자연 과학과 사회 과학의 많은 문제들에 역사적으로, 점 t∈ T{\displaystyle t\in T}시간의 뜻이 있어서 X(t){X(t)\displaystyle}은 확률 변수 값을 .[134] 통계적 과정 또한{X(t, ω):는 과목은 ∈ T}{\displaystyle\와 같이 같이 쓸 시간에 t{\displaystyle지}관찰을 나타내는입니다.{X(지 마,\ T TtT와의[29][135]2가지 변수의 함수임을 합니다
확률적 과정을 고려하는 다른 방법들이 있는데, 위의 정의는 전통적인 [69][70]것으로 간주된다.예를 들어, 확률 과정 또는 ST{\displaystyle S^{T}로 정의된}일 경우 확률 변수, ST{\displaystyle S^{T}}-valued 설정한 T{T\displaystyle}의 스페이스 S에 모든 가능한 기능{S\displaystyle}.[28][69] 하지만 이 대체 정의로 있는 공간 해석될 수 있다. ``func일반적으로 이온값 랜덤 변수"는 잘 [136]정의되어야 하는 추가적인 규칙성 가정을 필요로 한다.
인덱스 세트
T {\ T는 확률 프로세스의 인덱스 세트[4][52] 또는 파라미터[29][137] 세트라고 불립니다.대부분의 경우 이 세트는 자연수나 간격과 같은 실제 라인의 일부 서브셋이며 T T에 시간 [1]해석을 제공합니다.이 세트 외에도, 지수 T{T\displaystyle} 다른은 전체 오더나 데카르트 평면 같은 일반 set,[1][55]R2{\displaystyle R^{2}}또는 n원소 tT{\displaystyle t\in T}은 우주의 위치를 상징할 수 있{n\displaystyle}-dimensional 유클리드 공간, ∈로 설정할 수 있을까.[49][138]즉, 많은 결과와 정리는 완전히 순서가 정해진 지수 [139]집합을 가진 확률적 과정에서만 가능하다.
상태 공간
확률적 과정의 수학적 S S를 상태 공간이라고 합니다.이 수학적 공간은 정수, 실선, n차원 유클리드 공간, 복소 평면 또는 보다 추상적인 수학적 공간을 사용하여 정의할 수 있습니다.상태 공간은 확률적 프로세스가 [1][5][29][52][57]취할 수 있는 다양한 값을 반영하는 요소를 사용하여 정의됩니다.
샘플 함수
샘플 함수는 확률 프로세스의 단일 결과이므로 확률 프로세스의 [29][140]각 랜덤 변수의 단일 가능한 값을 취함으로써 형성된다.보다 는 {X ( , ) : T { \ { ( , \ ) : t \ T \ }} 이 확률적 프로세스라면 {\ \ \ \ Omega 의 매핑은 다음과 같습니다.
.[51]이것은 고정된 ω ∈Ω{\displaystyle\omega\in \Omega}에는 이용한 표본 함수가 존재하다는 것을 의미하는 표본 함수, 구현, 또는, 특히 T{T\displaystyle}시간으로 해석됩니다, 확률 과정({\displaystyle\와 같이{X(t,\omega):t\in T\}}의 샘플 경로 호출됩니다aps상태 S S[29]에 색인 세트 T {\ T 확률적 프로세스의 샘플 함수의 다른 이름에는 궤적, 경로[141] 함수 또는 [142]경로가 포함됩니다.
증가
확률적 과정의 증가는 동일한 확률적 과정의 두 랜덤 변수 간의 차이입니다.시간으로 해석될 수 있는 지수 집합을 가진 확률적 과정의 경우, 증분은 확률적 과정이 특정 기간 동안 얼마나 변화하는지이다.For example, if is a stochastic process with state space and index set , then for any two non-negative numbers and 는 t2 { 2 X - 1 { 는 랜덤 [49][50]증분으로 S \ S- valueuement입니다.증분에 관심이 있는 경우 상태 S S는 종종 실선 또는 자연수이지만 n n차원 유클리드 공간 또는 바나흐 공간 [50]등의 추상 공간일 수 .
추가 정의
법
프로세스 : δ T{\ X S 확률 공간 (δ F) \ {\\)에서 정의된 확률적 X의 법칙은 과 같다.
서 P P는 확률 측도이고 기호는 함수 구성을 X- 1(\})은 측정 가능 함수의 사전 이미지 또는 이에 상응하는(\}) 값 변수 X(\ X입니다.{\}}는 tT {\ T T에서 한 모든S {\ S 값 함수의 공간이므로 확률적 과정의 법칙은 확률 [28][69][143][144]측도이다
의 가능한 B(\S에 대해 X X의 사전 이미지는 다음과 같습니다.
의 법칙은 다음과 [29]같이 기술할 수 있습니다.
확률 과정 또는 랜덤 변수의 법칙을 확률 법칙, 확률 분포 또는 [134][143][145][146][147]분포라고도 합니다.
유한 차원 확률 분포
μ {\ \mu인 확률적 X {\ 의 t1, † {T에 유한 차원 분포는 다음과 같이 정의됩니다.
이 1,.. , n \ _ { 1} , . , 은 랜덤벡터 ( ( ) , , ( n) \ style ( ( { _ { { ) , \ , ( { t _ n ) )itionionionionionionionionionionionionionion 、 X ( X ( { { { { n } ) ) 、 { t _ { t _ { n } ) ) thisionion{ionionionionionionionionionionion T[28][148] 입니다.
n배 데카르트 의측정 가능한 부분 C C에 대해 확률적 X 의 유한 차원 분포는 다음과 같이 [29]쓸 수 있다.
확률적 과정의 유한 차원 분포는 일관성 [58]조건으로 알려진 두 가지 수학적 조건을 충족합니다.
정상성
정상성은 확률적 과정의 모든 랜덤 변수가 동등하게 분포될 때 확률적 과정이 갖는 수학적 특성이다.즉 X { X가 정지 확률 프로세스인 의 tT { t \ T} any any x X t { x x x x x thethe x the xthe x x x the x x x x x in x x x x x X _ { _ { t } t t t t t t t t t inutionutionutionutionutionutionutionutionution t t t,, in in in in t t t t in in in in in in in in 하는n개의 변수
모두 같은 확률 분포를 가지고 있습니다.정상 확률 과정의 지수 집합은 일반적으로 시간으로 해석되므로 정수 또는 [149][150]실선이 될 수 있습니다.그러나 지수 집합이 [149][151][152]시간으로 해석되지 않는 점 프로세스와 랜덤 필드에도 정상성의 개념이 존재합니다.
지수 T {\ T를 시간으로 해석할 수 있을 때, 시간의 환산 하에서 유한 차원 분포가 불변하면 확률적 과정은 정지되어 있다고 한다.이러한 유형의 확률적 과정은 정상 상태에 있지만 여전히 무작위 [149]변동을 경험하는 물리적 시스템을 설명하는 데 사용될 수 있다.정상성 뒤에 있는 직관은 시간이 경과함에 따라 정상 확률 과정의 분포가 [153]그대로 유지된다는 것이다.랜덤 변수의 시퀀스는 랜덤 변수가 균등하게 [149]분포되어 있는 경우에만 정상 확률 과정을 형성합니다.
정상성의 위와 같은 정의를 가진 확률적 과정은 때때로 완전히 정지 상태라고 하지만, 다른 형태의 정상성(stationality)이 있다.예를 들어 이산 시간 또는 연속 시간 확률 X(\ X가 넓은 의미에서 정지되어 있다고 할 때 (\X)는 t T에 대해 유한한 초의 모멘트와 두 랜덤 X의 공분산을 갖는다. t+(\는 에 대해 hh[153][154]에만 의존합니다.Khinchin은 넓은 의미에서의 관련 고정 개념을 도입했습니다.이것은 공분산 고정성이나 고정성을 포함한 다른 이름을 넓은 [154][155]의미입니다.
여과
여과는 일부 확률 공간과 관련하여 정의된 시그마 대수열의 증가 수열로, 예를 들어 지수 집합이 실수의 일부 부분 집합인 경우처럼, 총 순서 관계가 있는 지수 집합입니다.보다 형식적으로 확률적 프로세스에 총 순서가 설정된 인덱스가 있는 경우 확률 공간 P {\displaystyle {t}\}t\T {displaystyle {\ { { {\cal} {\cal {\cal} {\cal} {\cal} {\cal} {\cal} {\cal} {\cal} {\cal} {}어디지 마, s∈ T{\displaystyle t,s\in T}과≤{\displaystyle \leq}인덱스를 주문 총액은 여과의 개념이 T{T\displaystyle}.[52]을 세웠다를 의미한다 모든 s≤ t{\displaystyles\leq지},에{\displaystyle{{F\mathcal}}_{s}\subseteq}{{F\mathcal}_{t}\subseteq{{F\mathcal}}}, stu는 것이 가능하다.dy지t로 할 수 있는 확률 X t [52][156]에 포함된 의 양입니다 t tt}) 필터링의 이면에 있는 직관은 t t가 에 따라 X 에 대한 정보가 점점 더 많이 알려지거나 사용 가능해지며, F {t}로 캡처되어 분할이 미세화됩니다.f \ \ [157][158] 。
수정.
확률적 과정의 수정은 원래의 확률적 과정과 밀접한 관련이 있는 또 다른 확률적 과정이다.보다 정확하게는 다른 확률 와 동일한 색인 T(\ T S(\ S 및 확률공간 style {\을 갖는 확률 X(\X를 수정이라고 한다.Y는 에 대해
홀드. 서로 변형된 두 확률적 과정은 같은 유한 차원 법칙을[159] 가지며 확률적으로 등가 또는 [160]등가라고 한다.
두 확률 과정이 같은 유한 차원의. 분배지만 몇몇 작가들은 그 말 버전에 집중한다 수정 대신, 그 용어 버전도 다른 확률 공간 마련에 서로 이렇게 서로의 수정 두가지 과정도 버전에는 la.에서 정의될 수 있used,[151][161][162][163]은tter이지만,지 않정반대[164][143]
연속 시간 실시간 확률 과정이 그 증분으로 특정 모멘트 조건을 충족한다면, 콜모고로프 연속성 정리는 확률 1을 가진 연속 표본 경로를 가진 이 과정의 수정이 존재한다고 말하고, 따라서 확률 과정은 연속적인 수정 또는 [162][163][165]버전을 가집니다.또한 이 정리는 랜덤 필드로 일반화될 수 있으므로 지수 은 n n차원 유클리드[166] 공간일 뿐만 아니라 메트릭 공간을 [167]상태 공간으로 하는 확률적 과정에도 적용할 수 있다.
구별할 수 없다
동일한 확률공간 에 정의된 2개의 프로세스X(\X와 Y를 T 와 S(\ S로 구분할 수 없는 경우 다음과 같다.
고정.[143][159] 두 의 X X와 Y Y가 서로 변형된 것이며 거의 연속적인 경우X( 스타일X)와Y( 스타일 Y는 할 [168]수 없습니다.
분리 가능성
분리 가능성은 확률 측도와 관련하여 설정된 지수에 기초한 확률적 과정의 특성이다.속성은 확률적 과정이나 셀 수 없는 지수 집합을 가진 랜덤 필드의 기능이 랜덤 변수를 형성할 수 있도록 가정한다.확률적 과정이 분리 가능하기 위해서는 다른 조건과 더불어 지수 집합은 분리 [b]가능 공간이어야 한다. 즉, 지수 집합이 조밀한 계수 가능 [151][169]부분 집합을 갖는다는 것을 의미한다.
보다 정확하게는, 확률 공간 {\ {\을 가지는 실수치 연속 확률 X(\ X의 인덱스 T {\ T가 조밀하고 셀 수 있는 U U를 있는 경우 분리할 수 있다. _ \Omega}, P 0 (\ P_{0}= 즉 모든 집합 GT R (- F G U { { \ { _ { } \ { \ { } } } G t 、 { \ { _ { } \ F { { for } } } G} t t t t t t G display display display display display display display display display display display t t t t display t t t 또한[c] 분리성의 정의는 인덱스 세트와 상태 공간이 n n\ n차원 유클리드 [31][151]일 수 있는 랜덤 필드의 경우와 같이 다른 인덱스 세트와 상태 [175]공간에 대해서도 언급할 수 있다.
확률적 과정의 분리 가능성 개념은 조셉 두브에 의해 도입되었다.[169]분리 가능성에 대한 기본 개념은 지수 집합의 계수 가능한 점 집합이 확률적 [173]과정의 속성을 결정하도록 만드는 것이다.계수 가능한 지수 세트를 가진 확률적 프로세스는 이미 분리 가능성 조건을 충족하므로 이산 시간 확률 프로세스는 항상 분리할 [176]수 있다.Doob의 정리, 때때로 Doob의 분리 가능성 정리라고 알려진, Doob의 정리에 따르면, 어떤 실값 연속 시간 확률 과정도 분리 가능한 수정이 [169][171][177]있다고 합니다.이 정리의 버전은 또한 지수 집합과 실제 [137]선 이외의 상태 공간을 가진 보다 일반적인 확률 과정을 위해 존재한다.
인디펜던스
동일한 인덱스 T {\ T를 가진 동일한 확률 공간 에 정의된 2개의 확률 X X 및(\는 모든 N에 대해 독립적이라고 합니다. , T _ , \, \ T}, 랜덤벡터 ( ( ), …, ( )\ style \ ( _ {1 ) , \ ( t { ) \ ) 、 、 、 、 1 、 、
Two stochastic processes and are called uncorrelated if their cross-covariance is zero for all times.[179]: p. 142 Formally:
- .
If two stochastic processes and are independent, then they are also uncorrelated.[179]: p. 151
Orthogonality
Two stochastic processes and are called orthogonal if their cross-correlation is zero for all times.[179]: p. 142 Formally:
- .
Skorokhod space
A Skorokhod space, also written as Skorohod space, is a mathematical space of all the functions that are right-continuous with left limits, defined on some interval of the real line such as or , and take values on the real line or on some metric space.[180][181][182] Such functions are known as càdlàg or cadlag functions, based on the acronym of the French phrase continue à droite, limite à gauche.[180][183] A Skorokhod function space, introduced by Anatoliy Skorokhod,[182] is often denoted with the letter ,[180][181][182][183] so the function space is also referred to as space .[180][184][185] The notation of this function space can also include the interval on which all the càdlàg functions are defined, so, for example, denotes the space of càdlàg functions defined on the unit interval .[183][185][186]
Skorokhod function spaces are frequently used in the theory of stochastic processes because it often assumed that the sample functions of continuous-time stochastic processes belong to a Skorokhod space.[182][184] Such spaces contain continuous functions, which correspond to sample functions of the Wiener process. But the space also has functions with discontinuities, which means that the sample functions of stochastic processes with jumps, such as the Poisson process (on the real line), are also members of this space.[185][187]
Regularity
In the context of mathematical construction of stochastic processes, the term regularity is used when discussing and assuming certain conditions for a stochastic process to resolve possible construction issues.[188][189] For example, to study stochastic processes with uncountable index sets, it is assumed that the stochastic process adheres to some type of regularity condition such as the sample functions being continuous.[190][191]
Further examples
Markov processes and chains
Markov processes are stochastic processes, traditionally in discrete or continuous time, that have the Markov property, which means the next value of the Markov process depends on the current value, but it is conditionally independent of the previous values of the stochastic process. In other words, the behavior of the process in the future is stochastically independent of its behavior in the past, given the current state of the process.[192][193]
The Brownian motion process and the Poisson process (in one dimension) are both examples of Markov processes[194] in continuous time, while random walks on the integers and the gambler's ruin problem are examples of Markov processes in discrete time.[195][196]
A Markov chain is a type of Markov process that has either discrete state space or discrete index set (often representing time), but the precise definition of a Markov chain varies.[197] For example, it is common to define a Markov chain as a Markov process in either discrete or continuous time with a countable state space (thus regardless of the nature of time),[198][199][200][201] but it has been also common to define a Markov chain as having discrete time in either countable or continuous state space (thus regardless of the state space).[197] It has been argued that the first definition of a Markov chain, where it has discrete time, now tends to be used, despite the second definition having been used by researchers like Joseph Doob and Kai Lai Chung.[202]
Markov processes form an important class of stochastic processes and have applications in many areas.[40][203] For example, they are the basis for a general stochastic simulation method known as Markov chain Monte Carlo, which is used for simulating random objects with specific probability distributions, and has found application in Bayesian statistics.[204][205]
The concept of the Markov property was originally for stochastic processes in continuous and discrete time, but the property has been adapted for other index sets such as -dimensional Euclidean space, which results in collections of random variables known as Markov random fields.[206][207][208]
Martingale
A martingale is a discrete-time or continuous-time stochastic process with the property that, at every instant, given the current value and all the past values of the process, the conditional expectation of every future value is equal to the current value. In discrete time, if this property holds for the next value, then it holds for all future values. The exact mathematical definition of a martingale requires two other conditions coupled with the mathematical concept of a filtration, which is related to the intuition of increasing available information as time passes. Martingales are usually defined to be real-valued,[209][210][156] but they can also be complex-valued[211] or even more general.[212]
A symmetric random walk and a Wiener process (with zero drift) are both examples of martingales, respectively, in discrete and continuous time.[209][210] For a sequence of independent and identically distributed random variables with zero mean, the stochastic process formed from the successive partial sums is a discrete-time martingale.[213] In this aspect, discrete-time martingales generalize the idea of partial sums of independent random variables.[214]
Martingales can also be created from stochastic processes by applying some suitable transformations, which is the case for the homogeneous Poisson process (on the real line) resulting in a martingale called the compensated Poisson process.[210] Martingales can also be built from other martingales.[213] For example, there are martingales based on the martingale the Wiener process, forming continuous-time martingales.[209][215]
Martingales mathematically formalize the idea of a fair game,[216] and they were originally developed to show that it is not possible to win a fair game.[217] But now they are used in many areas of probability, which is one of the main reasons for studying them.[156][217][218] Many problems in probability have been solved by finding a martingale in the problem and studying it.[219] Martingales will converge, given some conditions on their moments, so they are often used to derive convergence results, due largely to martingale convergence theorems.[214][220][221]
Martingales have many applications in statistics, but it has been remarked that its use and application are not as widespread as it could be in the field of statistics, particularly statistical inference.[222] They have found applications in areas in probability theory such as queueing theory and Palm calculus[223] and other fields such as economics[224] and finance.[18]
Lévy process
Lévy processes are types of stochastic processes that can be considered as generalizations of random walks in continuous time.[50][225] These processes have many applications in fields such as finance, fluid mechanics, physics and biology.[226][227] The main defining characteristics of these processes are their stationarity and independence properties, so they were known as processes with stationary and independent increments. In other words, a stochastic process is a Lévy process if for non-negatives numbers, , the corresponding increments
are all independent of each other, and the distribution of each increment only depends on the difference in time.[50]
A Lévy process can be defined such that its state space is some abstract mathematical space, such as a Banach space, but the processes are often defined so that they take values in Euclidean space. The index set is the non-negative numbers, so , which gives the interpretation of time. Important stochastic processes such as the Wiener process, the homogeneous Poisson process (in one dimension), and subordinators are all Lévy processes.[50][225]
Random field
A random field is a collection of random variables indexed by a -dimensional Euclidean space or some manifold. In general, a random field can be considered an example of a stochastic or random process, where the index set is not necessarily a subset of the real line.[31] But there is a convention that an indexed collection of random variables is called a random field when the index has two or more dimensions.[5][29][228] If the specific definition of a stochastic process requires the index set to be a subset of the real line, then the random field can be considered as a generalization of stochastic process.[229]
Point process
A point process is a collection of points randomly located on some mathematical space such as the real line, -dimensional Euclidean space, or more abstract spaces. Sometimes the term point process is not preferred, as historically the word process denoted an evolution of some system in time, so a point process is also called a random point field.[230] There are different interpretations of a point process, such a random counting measure or a random set.[231][232] Some authors regard a point process and stochastic process as two different objects such that a point process is a random object that arises from or is associated with a stochastic process,[233][234] though it has been remarked that the difference between point processes and stochastic processes is not clear.[234]
Other authors consider a point process as a stochastic process, where the process is indexed by sets of the underlying space[d] on which it is defined, such as the real line or -dimensional Euclidean space.[237][238] Other stochastic processes such as renewal and counting processes are studied in the theory of point processes.[239][234]
History
Early probability theory
Probability theory has its origins in games of chance, which have a long history, with some games being played thousands of years ago,[240][241] but very little analysis on them was done in terms of probability.[240][242] The year 1654 is often considered the birth of probability theory when French mathematicians Pierre Fermat and Blaise Pascal had a written correspondence on probability, motivated by a gambling problem.[240][243][244] But there was earlier mathematical work done on the probability of gambling games such as Liber de Ludo Aleae by Gerolamo Cardano, written in the 16th century but posthumously published later in 1663.[240][245]
After Cardano, Jakob Bernoulli[e] wrote Ars Conjectandi, which is considered a significant event in the history of probability theory.[240] Bernoulli's book was published, also posthumously, in 1713 and inspired many mathematicians to study probability.[240][247][248] But despite some renowned mathematicians contributing to probability theory, such as Pierre-Simon Laplace, Abraham de Moivre, Carl Gauss, Siméon Poisson and Pafnuty Chebyshev,[249][250] most of the mathematical community[f] did not consider probability theory to be part of mathematics until the 20th century.[249][251][252][253]
Statistical mechanics
In the physical sciences, scientists developed in the 19th century the discipline of statistical mechanics, where physical systems, such as containers filled with gases, can be regarded or treated mathematically as collections of many moving particles. Although there were attempts to incorporate randomness into statistical physics by some scientists, such as Rudolf Clausius, most of the work had little or no randomness.[254][255] This changed in 1859 when James Clerk Maxwell contributed significantly to the field, more specifically, to the kinetic theory of gases, by presenting work where he assumed the gas particles move in random directions at random velocities.[256][257] The kinetic theory of gases and statistical physics continued to be developed in the second half of the 19th century, with work done chiefly by Clausius, Ludwig Boltzmann and Josiah Gibbs, which would later have an influence on Albert Einstein's mathematical model for Brownian movement.[258]
Measure theory and probability theory
At the International Congress of Mathematicians in Paris in 1900, David Hilbert presented a list of mathematical problems, where his sixth problem asked for a mathematical treatment of physics and probability involving axioms.[250] Around the start of the 20th century, mathematicians developed measure theory, a branch of mathematics for studying integrals of mathematical functions, where two of the founders were French mathematicians, Henri Lebesgue and Émile Borel. In 1925 another French mathematician Paul Lévy published the first probability book that used ideas from measure theory.[250]
In 1920s fundamental contributions to probability theory were made in the Soviet Union by mathematicians such as Sergei Bernstein, Aleksandr Khinchin,[g] and Andrei Kolmogorov.[253] Kolmogorov published in 1929 his first attempt at presenting a mathematical foundation, based on measure theory, for probability theory.[259] In the early 1930s Khinchin and Kolmogorov set up probability seminars, which were attended by researchers such as Eugene Slutsky and Nikolai Smirnov,[260] and Khinchin gave the first mathematical definition of a stochastic process as a set of random variables indexed by the real line.[64][261][h]
Birth of modern probability theory
In 1933 Andrei Kolmogorov published in German, his book on the foundations of probability theory titled Grundbegriffe der Wahrscheinlichkeitsrechnung,[i] where Kolmogorov used measure theory to develop an axiomatic framework for probability theory. The publication of this book is now widely considered to be the birth of modern probability theory, when the theories of probability and stochastic processes became parts of mathematics.[250][253]
After the publication of Kolmogorov's book, further fundamental work on probability theory and stochastic processes was done by Khinchin and Kolmogorov as well as other mathematicians such as Joseph Doob, William Feller, Maurice Fréchet, Paul Lévy, Wolfgang Doeblin, and Harald Cramér.[250][253] Decades later Cramér referred to the 1930s as the "heroic period of mathematical probability theory".[253] World War II greatly interrupted the development of probability theory, causing, for example, the migration of Feller from Sweden to the United States of America[253] and the death of Doeblin, considered now a pioneer in stochastic processes.[263]

Stochastic processes after World War II
After World War II the study of probability theory and stochastic processes gained more attention from mathematicians, with significant contributions made in many areas of probability and mathematics as well as the creation of new areas.[253][266] Starting in the 1940s, Kiyosi Itô published papers developing the field of stochastic calculus, which involves stochastic integrals and stochastic differential equations based on the Wiener or Brownian motion process.[267]
Also starting in the 1940s, connections were made between stochastic processes, particularly martingales, and the mathematical field of potential theory, with early ideas by Shizuo Kakutani and then later work by Joseph Doob.[266] Further work, considered pioneering, was done by Gilbert Hunt in the 1950s, connecting Markov processes and potential theory, which had a significant effect on the theory of Lévy processes and led to more interest in studying Markov processes with methods developed by Itô.[22][268][269]
In 1953 Doob published his book Stochastic processes, which had a strong influence on the theory of stochastic processes and stressed the importance of measure theory in probability.[266] [265] Doob also chiefly developed the theory of martingales, with later substantial contributions by Paul-André Meyer. Earlier work had been carried out by Sergei Bernstein, Paul Lévy and Jean Ville, the latter adopting the term martingale for the stochastic process.[270][271] Methods from the theory of martingales became popular for solving various probability problems. Techniques and theory were developed to study Markov processes and then applied to martingales. Conversely, methods from the theory of martingales were established to treat Markov processes.[266]
Other fields of probability were developed and used to study stochastic processes, with one main approach being the theory of large deviations.[266] The theory has many applications in statistical physics, among other fields, and has core ideas going back to at least the 1930s. Later in the 1960s and 1970s fundamental work was done by Alexander Wentzell in the Soviet Union and Monroe D. Donsker and Srinivasa Varadhan in the United States of America,[272] which would later result in Varadhan winning the 2007 Abel Prize.[273] In the 1990s and 2000s the theories of Schramm–Loewner evolution[274] and rough paths[143] were introduced and developed to study stochastic processes and other mathematical objects in probability theory, which respectively resulted in Fields Medals being awarded to Wendelin Werner[275] in 2008 and to Martin Hairer in 2014.[276]
The theory of stochastic processes still continues to be a focus of research, with yearly international conferences on the topic of stochastic processes.[46][226]
Discoveries of specific stochastic processes
Although Khinchin gave mathematical definitions of stochastic processes in the 1930s,[64][261] specific stochastic processes had already been discovered in different settings, such as the Brownian motion process and the Poisson process.[22][25] Some families of stochastic processes such as point processes or renewal processes have long and complex histories, stretching back centuries.[277]
Bernoulli process
The Bernoulli process, which can serve as a mathematical model for flipping a biased coin, is possibly the first stochastic process to have been studied.[82] The process is a sequence of independent Bernoulli trials,[83] which are named after Jackob Bernoulli who used them to study games of chance, including probability problems proposed and studied earlier by Christiaan Huygens.[278] Bernoulli's work, including the Bernoulli process, were published in his book Ars Conjectandi in 1713.[279]
Random walks
In 1905 Karl Pearson coined the term random walk while posing a problem describing a random walk on the plane, which was motivated by an application in biology, but such problems involving random walks had already been studied in other fields. Certain gambling problems that were studied centuries earlier can be considered as problems involving random walks.[90][279] For example, the problem known as the Gambler's ruin is based on a simple random walk,[196][280] and is an example of a random walk with absorbing barriers.[243][281] Pascal, Fermat and Huyens all gave numerical solutions to this problem without detailing their methods,[282] and then more detailed solutions were presented by Jakob Bernoulli and Abraham de Moivre.[283]
For random walks in -dimensional integer lattices, George Pólya published, in 1919 and 1921, work where he studied the probability of a symmetric random walk returning to a previous position in the lattice. Pólya showed that a symmetric random walk, which has an equal probability to advance in any direction in the lattice, will return to a previous position in the lattice an infinite number of times with probability one in one and two dimensions, but with probability zero in three or higher dimensions.[284][285]
Wiener process
The Wiener process or Brownian motion process has its origins in different fields including statistics, finance and physics.[22] In 1880, Thorvald Thiele wrote a paper on the method of least squares, where he used the process to study the errors of a model in time-series analysis.[286][287][288] The work is now considered as an early discovery of the statistical method known as Kalman filtering, but the work was largely overlooked. It is thought that the ideas in Thiele's paper were too advanced to have been understood by the broader mathematical and statistical community at the time.[288]

The French mathematician Louis Bachelier used a Wiener process in his 1900 thesis[289][290] in order to model price changes on the Paris Bourse, a stock exchange,[291] without knowing the work of Thiele.[22] It has been speculated that Bachelier drew ideas from the random walk model of Jules Regnault, but Bachelier did not cite him,[292] and Bachelier's thesis is now considered pioneering in the field of financial mathematics.[291][292]
It is commonly thought that Bachelier's work gained little attention and was forgotten for decades until it was rediscovered in the 1950s by the Leonard Savage, and then become more popular after Bachelier's thesis was translated into English in 1964. But the work was never forgotten in the mathematical community, as Bachelier published a book in 1912 detailing his ideas,[292] which was cited by mathematicians including Doob, Feller[292] and Kolmogorov.[22] The book continued to be cited, but then starting in the 1960s the original thesis by Bachelier began to be cited more than his book when economists started citing Bachelier's work.[292]
In 1905 Albert Einstein published a paper where he studied the physical observation of Brownian motion or movement to explain the seemingly random movements of particles in liquids by using ideas from the kinetic theory of gases. Einstein derived a differential equation, known as a diffusion equation, for describing the probability of finding a particle in a certain region of space. Shortly after Einstein's first paper on Brownian movement, Marian Smoluchowski published work where he cited Einstein, but wrote that he had independently derived the equivalent results by using a different method.[293]
Einstein's work, as well as experimental results obtained by Jean Perrin, later inspired Norbert Wiener in the 1920s[294] to use a type of measure theory, developed by Percy Daniell, and Fourier analysis to prove the existence of the Wiener process as a mathematical object.[22]
Poisson process
The Poisson process is named after Siméon Poisson, due to its definition involving the Poisson distribution, but Poisson never studied the process.[23][295] There are a number of claims for early uses or discoveries of the Poisson process.[23][25] At the beginning of the 20th century the Poisson process would arise independently in different situations.[23][25] In Sweden 1903, Filip Lundberg published a thesis containing work, now considered fundamental and pioneering, where he proposed to model insurance claims with a homogeneous Poisson process.[296][297]
Another discovery occurred in Denmark in 1909 when A.K. Erlang derived the Poisson distribution when developing a mathematical model for the number of incoming phone calls in a finite time interval. Erlang was not at the time aware of Poisson's earlier work and assumed that the number phone calls arriving in each interval of time were independent to each other. He then found the limiting case, which is effectively recasting the Poisson distribution as a limit of the binomial distribution.[23]
In 1910 Ernest Rutherford and Hans Geiger published experimental results on counting alpha particles. Motivated by their work, Harry Bateman studied the counting problem and derived Poisson probabilities as a solution to a family of differential equations, resulting in the independent discovery of the Poisson process.[23] After this time there were many studies and applications of the Poisson process, but its early history is complicated, which has been explained by the various applications of the process in numerous fields by biologists, ecologists, engineers and various physical scientists.[23]
Markov processes
Markov processes and Markov chains are named after Andrey Markov who studied Markov chains in the early 20th century.[298] Markov was interested in studying an extension of independent random sequences.[298] In his first paper on Markov chains, published in 1906, Markov showed that under certain conditions the average outcomes of the Markov chain would converge to a fixed vector of values, so proving a weak law of large numbers without the independence assumption,[299] [300][301][302] which had been commonly regarded as a requirement for such mathematical laws to hold.[302] Markov later used Markov chains to study the distribution of vowels in Eugene Onegin, written by Alexander Pushkin, and proved a central limit theorem for such chains.[299][300]
In 1912 Poincaré studied Markov chains on finite groups with an aim to study card shuffling. Other early uses of Markov chains include a diffusion model, introduced by Paul and Tatyana Ehrenfest in 1907, and a branching process, introduced by Francis Galton and Henry William Watson in 1873, preceding the work of Markov.[300][301] After the work of Galton and Watson, it was later revealed that their branching process had been independently discovered and studied around three decades earlier by Irénée-Jules Bienaymé.[303] Starting in 1928, Maurice Fréchet became interested in Markov chains, eventually resulting in him publishing in 1938 a detailed study on Markov chains.[300][304]
Andrei Kolmogorov developed in a 1931 paper a large part of the early theory of continuous-time Markov processes.[253][259] Kolmogorov was partly inspired by Louis Bachelier's 1900 work on fluctuations in the stock market as well as Norbert Wiener's work on Einstein's model of Brownian movement.[259][305] He introduced and studied a particular set of Markov processes known as diffusion processes, where he derived a set of differential equations describing the processes.[259][306] Independent of Kolmogorov's work, Sydney Chapman derived in a 1928 paper an equation, now called the Chapman–Kolmogorov equation, in a less mathematically rigorous way than Kolmogorov, while studying Brownian movement.[307] The differential equations are now called the Kolmogorov equations[308] or the Kolmogorov–Chapman equations.[309] Other mathematicians who contributed significantly to the foundations of Markov processes include William Feller, starting in the 1930s, and then later Eugene Dynkin, starting in the 1950s.[253]
Lévy processes
Lévy processes such as the Wiener process and the Poisson process (on the real line) are named after Paul Lévy who started studying them in the 1930s,[226] but they have connections to infinitely divisible distributions going back to the 1920s.[225] In a 1932 paper Kolmogorov derived a characteristic function for random variables associated with Lévy processes. This result was later derived under more general conditions by Lévy in 1934, and then Khinchin independently gave an alternative form for this characteristic function in 1937.[253][310] In addition to Lévy, Khinchin and Kolomogrov, early fundamental contributions to the theory of Lévy processes were made by Bruno de Finetti and Kiyosi Itô.[225]
Mathematical construction
In mathematics, constructions of mathematical objects are needed, which is also the case for stochastic processes, to prove that they exist mathematically.[58] There are two main approaches for constructing a stochastic process. One approach involves considering a measurable space of functions, defining a suitable measurable mapping from a probability space to this measurable space of functions, and then deriving the corresponding finite-dimensional distributions.[311]
Another approach involves defining a collection of random variables to have specific finite-dimensional distributions, and then using Kolmogorov's existence theorem[j] to prove a corresponding stochastic process exists.[58][311] This theorem, which is an existence theorem for measures on infinite product spaces,[315] says that if any finite-dimensional distributions satisfy two conditions, known as consistency conditions, then there exists a stochastic process with those finite-dimensional distributions.[58]
Construction issues
When constructing continuous-time stochastic processes certain mathematical difficulties arise, due to the uncountable index sets, which do not occur with discrete-time processes.[59][60] One problem is that is it possible to have more than one stochastic process with the same finite-dimensional distributions. For example, both the left-continuous modification and the right-continuous modification of a Poisson process have the same finite-dimensional distributions.[316] This means that the distribution of the stochastic process does not, necessarily, specify uniquely the properties of the sample functions of the stochastic process.[311][317]
Another problem is that functionals of continuous-time process that rely upon an uncountable number of points of the index set may not be measurable, so the probabilities of certain events may not be well-defined.[169] For example, the supremum of a stochastic process or random field is not necessarily a well-defined random variable.[31][60] For a continuous-time stochastic process , other characteristics that depend on an uncountable number of points of the index set include:[169]
- a sample function of a stochastic process is a continuous function of ;
- a sample function of a stochastic process is a bounded function of ; and
- a sample function of a stochastic process is an increasing function of .
To overcome these two difficulties, different assumptions and approaches are possible.[70]
Resolving construction issues
One approach for avoiding mathematical construction issues of stochastic processes, proposed by Joseph Doob, is to assume that the stochastic process is separable.[318] Separability ensures that infinite-dimensional distributions determine the properties of sample functions by requiring that sample functions are essentially determined by their values on a dense countable set of points in the index set.[319] Furthermore, if a stochastic process is separable, then functionals of an uncountable number of points of the index set are measurable and their probabilities can be studied.[169][319]
Another approach is possible, originally developed by Anatoliy Skorokhod and Andrei Kolmogorov,[320] for a continuous-time stochastic process with any metric space as its state space. For the construction of such a stochastic process, it is assumed that the sample functions of the stochastic process belong to some suitable function space, which is usually the Skorokhod space consisting of all right-continuous functions with left limits. This approach is now more used than the separability assumption,[70][264] but such a stochastic process based on this approach will be automatically separable.[321]
Although less used, the separability assumption is considered more general because every stochastic process has a separable version.[264] It is also used when it is not possible to construct a stochastic process in a Skorokhod space.[174] For example, separability is assumed when constructing and studying random fields, where the collection of random variables is now indexed by sets other than the real line such as -dimensional Euclidean space.[31][322]
See also
- List of stochastic processes topics
- Covariance function
- Deterministic system
- Dynamics of Markovian particles
- Entropy rate (for a stochastic process)
- Ergodic process
- GenI process
- Gillespie algorithm
- Interacting particle system
- Law (stochastic processes)
- Markov chain
- Probabilistic cellular automaton
- Random field
- Randomness
- Stationary process
- Statistical model
- Stochastic calculus
- Stochastic control
- Stochastic processes and boundary value problems
Notes
- ^ The term Brownian motion can refer to the physical process, also known as Brownian movement, and the stochastic process, a mathematical object, but to avoid ambiguity this article uses the terms Brownian motion process or Wiener process for the latter in a style similar to, for example, Gikhman and Skorokhod[20] or Rosenblatt.[21]
- ^ The term "separable" appears twice here with two different meanings, where the first meaning is from probability and the second from topology and analysis. For a stochastic process to be separable (in a probabilistic sense), its index set must be a separable space (in a topological or analytic sense), in addition to other conditions.[137]
- ^ The definition of separability for a continuous-time real-valued stochastic process can be stated in other ways.[173][174]
- ^ In the context of point processes, the term "state space" can mean the space on which the point process is defined such as the real line,[235][236] which corresponds to the index set in stochastic process terminology.
- ^ Also known as James or Jacques Bernoulli.[246]
- ^ It has been remarked that a notable exception was the St Petersburg School in Russia, where mathematicians led by Chebyshev studied probability theory.[251]
- ^ The name Khinchin is also written in (or transliterated into) English as Khintchine.[64]
- ^ Doob, when citing Khinchin, uses the term 'chance variable', which used to be an alternative term for 'random variable'.[262]
- ^ Later translated into English and published in 1950 as Foundations of the Theory of Probability[250]
- ^ The theorem has other names including Kolmogorov's consistency theorem,[312] Kolmogorov's extension theorem[313] or the Daniell–Kolmogorov theorem.[314]
References
- ^ a b c d e f g h i Joseph L. Doob (1990). Stochastic processes. Wiley. pp. 46, 47.
- ^ a b c d L. C. G. Rogers; David Williams (2000). Diffusions, Markov Processes, and Martingales: Volume 1, Foundations. Cambridge University Press. p. 1. ISBN 978-1-107-71749-7.
- ^ a b c J. Michael Steele (2012). Stochastic Calculus and Financial Applications. Springer Science & Business Media. p. 29. ISBN 978-1-4684-9305-4.
- ^ a b c d e Emanuel Parzen (2015). Stochastic Processes. Courier Dover Publications. pp. 7, 8. ISBN 978-0-486-79688-8.
- ^ a b c d e f g h i j k l Iosif Ilyich Gikhman; Anatoly Vladimirovich Skorokhod (1969). Introduction to the Theory of Random Processes. Courier Corporation. p. 1. ISBN 978-0-486-69387-3.
- ^ Paul C. Bressloff (2014). Stochastic Processes in Cell Biology. Springer. ISBN 978-3-319-08488-6.
- ^ N.G. Van Kampen (2011). Stochastic Processes in Physics and Chemistry. Elsevier. ISBN 978-0-08-047536-3.
- ^ Russell Lande; Steinar Engen; Bernt-Erik Sæther (2003). Stochastic Population Dynamics in Ecology and Conservation. Oxford University Press. ISBN 978-0-19-852525-7.
- ^ Carlo Laing; Gabriel J Lord (2010). Stochastic Methods in Neuroscience. OUP Oxford. ISBN 978-0-19-923507-0.
- ^ Wolfgang Paul; Jörg Baschnagel (2013). Stochastic Processes: From Physics to Finance. Springer Science & Business Media. ISBN 978-3-319-00327-6.
- ^ Edward R. Dougherty (1999). Random processes for image and signal processing. SPIE Optical Engineering Press. ISBN 978-0-8194-2513-3.
- ^ Dimitri P. Bertsekas (1996). Stochastic Optimal Control: The Discrete-Time Case. Athena Scientific. ISBN 1-886529-03-5.
- ^ Thomas M. Cover; Joy A. Thomas (2012). Elements of Information Theory. John Wiley & Sons. p. 71. ISBN 978-1-118-58577-1.
- ^ Michael Baron (2015). Probability and Statistics for Computer Scientists, Second Edition. CRC Press. p. 131. ISBN 978-1-4987-6060-7.
- ^ Jonathan Katz; Yehuda Lindell (2007). Introduction to Modern Cryptography: Principles and Protocols. CRC Press. p. 26. ISBN 978-1-58488-586-3.
- ^ François Baccelli; Bartlomiej Blaszczyszyn (2009). Stochastic Geometry and Wireless Networks. Now Publishers Inc. ISBN 978-1-60198-264-3.
- ^ J. Michael Steele (2001). Stochastic Calculus and Financial Applications. Springer Science & Business Media. ISBN 978-0-387-95016-7.
- ^ a b Marek Musiela; Marek Rutkowski (2006). Martingale Methods in Financial Modelling. Springer Science & Business Media. ISBN 978-3-540-26653-2.
- ^ Steven E. Shreve (2004). Stochastic Calculus for Finance II: Continuous-Time Models. Springer Science & Business Media. ISBN 978-0-387-40101-0.
- ^ Iosif Ilyich Gikhman; Anatoly Vladimirovich Skorokhod (1969). Introduction to the Theory of Random Processes. Courier Corporation. ISBN 978-0-486-69387-3.
- ^ Murray Rosenblatt (1962). Random Processes. Oxford University Press.
- ^ a b c d e f g h i Jarrow, Robert; Protter, Philip (2004). "A short history of stochastic integration and mathematical finance: the early years, 1880–1970". A Festschrift for Herman Rubin. Institute of Mathematical Statistics Lecture Notes - Monograph Series. pp. 75–80. CiteSeerX 10.1.1.114.632. doi:10.1214/lnms/1196285381. ISBN 978-0-940600-61-4. ISSN 0749-2170.
- ^ a b c d e f g h Stirzaker, David (2000). "Advice to Hedgehogs, or, Constants Can Vary". The Mathematical Gazette. 84 (500): 197–210. doi:10.2307/3621649. ISSN 0025-5572. JSTOR 3621649. S2CID 125163415.
- ^ Donald L. Snyder; Michael I. Miller (2012). Random Point Processes in Time and Space. Springer Science & Business Media. p. 32. ISBN 978-1-4612-3166-0.
- ^ a b c d Guttorp, Peter; Thorarinsdottir, Thordis L. (2012). "What Happened to Discrete Chaos, the Quenouille Process, and the Sharp Markov Property? Some History of Stochastic Point Processes". International Statistical Review. 80 (2): 253–268. doi:10.1111/j.1751-5823.2012.00181.x. ISSN 0306-7734. S2CID 80836.
- ^ Gusak, Dmytro; Kukush, Alexander; Kulik, Alexey; Mishura, Yuliya; Pilipenko, Andrey (2010). Theory of Stochastic Processes: With Applications to Financial Mathematics and Risk Theory. Springer Science & Business Media. p. 21. ISBN 978-0-387-87862-1.
- ^ Valeriy Skorokhod (2005). Basic Principles and Applications of Probability Theory. Springer Science & Business Media. p. 42. ISBN 978-3-540-26312-8.
- ^ a b c d e f Olav Kallenberg (2002). Foundations of Modern Probability. Springer Science & Business Media. pp. 24–25. ISBN 978-0-387-95313-7.
- ^ a b c d e f g h i j k l m n o p John Lamperti (1977). Stochastic processes: a survey of the mathematical theory. Springer-Verlag. pp. 1–2. ISBN 978-3-540-90275-1.
- ^ a b c d Loïc Chaumont; Marc Yor (2012). Exercises in Probability: A Guided Tour from Measure Theory to Random Processes, Via Conditioning. Cambridge University Press. p. 175. ISBN 978-1-107-60655-5.
- ^ a b c d e f g h Robert J. Adler; Jonathan E. Taylor (2009). Random Fields and Geometry. Springer Science & Business Media. pp. 7–8. ISBN 978-0-387-48116-6.
- ^ Gregory F. Lawler; Vlada Limic (2010). Random Walk: A Modern Introduction. Cambridge University Press. ISBN 978-1-139-48876-1.
- ^ David Williams (1991). Probability with Martingales. Cambridge University Press. ISBN 978-0-521-40605-5.
- ^ L. C. G. Rogers; David Williams (2000). Diffusions, Markov Processes, and Martingales: Volume 1, Foundations. Cambridge University Press. ISBN 978-1-107-71749-7.
- ^ David Applebaum (2004). Lévy Processes and Stochastic Calculus. Cambridge University Press. ISBN 978-0-521-83263-2.
- ^ Mikhail Lifshits (2012). Lectures on Gaussian Processes. Springer Science & Business Media. ISBN 978-3-642-24939-6.
- ^ Robert J. Adler (2010). The Geometry of Random Fields. SIAM. ISBN 978-0-89871-693-1.
- ^ Samuel Karlin; Howard E. Taylor (2012). A First Course in Stochastic Processes. Academic Press. ISBN 978-0-08-057041-9.
- ^ Bruce Hajek (2015). Random Processes for Engineers. Cambridge University Press. ISBN 978-1-316-24124-0.
- ^ a b G. Latouche; V. Ramaswami (1999). Introduction to Matrix Analytic Methods in Stochastic Modeling. SIAM. ISBN 978-0-89871-425-8.
- ^ D.J. Daley; David Vere-Jones (2007). An Introduction to the Theory of Point Processes: Volume II: General Theory and Structure. Springer Science & Business Media. ISBN 978-0-387-21337-8.
- ^ Patrick Billingsley (2008). Probability and Measure. Wiley India Pvt. Limited. ISBN 978-81-265-1771-8.
- ^ Pierre Brémaud (2014). Fourier Analysis and Stochastic Processes. Springer. ISBN 978-3-319-09590-5.
- ^ Adam Bobrowski (2005). Functional Analysis for Probability and Stochastic Processes: An Introduction. Cambridge University Press. ISBN 978-0-521-83166-6.
- ^ Applebaum, David (2004). "Lévy processes: From probability to finance and quantum groups". Notices of the AMS. 51 (11): 1336–1347.
- ^ a b Jochen Blath; Peter Imkeller; Sylvie Roelly (2011). Surveys in Stochastic Processes. European Mathematical Society. ISBN 978-3-03719-072-2.
- ^ Michel Talagrand (2014). Upper and Lower Bounds for Stochastic Processes: Modern Methods and Classical Problems. Springer Science & Business Media. pp. 4–. ISBN 978-3-642-54075-2.
- ^ Paul C. Bressloff (2014). Stochastic Processes in Cell Biology. Springer. pp. vii–ix. ISBN 978-3-319-08488-6.
- ^ a b c d Samuel Karlin; Howard E. Taylor (2012). A First Course in Stochastic Processes. Academic Press. p. 27. ISBN 978-0-08-057041-9.
- ^ a b c d e f g h i j Applebaum, David (2004). "Lévy processes: From probability to finance and quantum groups". Notices of the AMS. 51 (11): 1337.
- ^ a b L. C. G. Rogers; David Williams (2000). Diffusions, Markov Processes, and Martingales: Volume 1, Foundations. Cambridge University Press. pp. 121–124. ISBN 978-1-107-71749-7.
- ^ a b c d e f Ionut Florescu (2014). Probability and Stochastic Processes. John Wiley & Sons. pp. 294, 295. ISBN 978-1-118-59320-2.
- ^ a b Samuel Karlin; Howard E. Taylor (2012). A First Course in Stochastic Processes. Academic Press. p. 26. ISBN 978-0-08-057041-9.
- ^ Donald L. Snyder; Michael I. Miller (2012). Random Point Processes in Time and Space. Springer Science & Business Media. pp. 24, 25. ISBN 978-1-4612-3166-0.
- ^ a b Patrick Billingsley (2008). Probability and Measure. Wiley India Pvt. Limited. p. 482. ISBN 978-81-265-1771-8.
- ^ a b Alexander A. Borovkov (2013). Probability Theory. Springer Science & Business Media. p. 527. ISBN 978-1-4471-5201-9.
- ^ a b c Pierre Brémaud (2014). Fourier Analysis and Stochastic Processes. Springer. p. 120. ISBN 978-3-319-09590-5.
- ^ a b c d e Jeffrey S Rosenthal (2006). A First Look at Rigorous Probability Theory. World Scientific Publishing Co Inc. pp. 177–178. ISBN 978-981-310-165-4.
- ^ a b Peter E. Kloeden; Eckhard Platen (2013). Numerical Solution of Stochastic Differential Equations. Springer Science & Business Media. p. 63. ISBN 978-3-662-12616-5.
- ^ a b c Davar Khoshnevisan (2006). Multiparameter Processes: An Introduction to Random Fields. Springer Science & Business Media. pp. 153–155. ISBN 978-0-387-21631-7.
- ^ a b "Stochastic". Oxford English Dictionary (Online ed.). Oxford University Press. (Subscription or participating institution membership required.)
- ^ O. B. Sheĭnin (2006). Theory of probability and statistics as exemplified in short dictums. NG Verlag. p. 5. ISBN 978-3-938417-40-9.
- ^ Oscar Sheynin; Heinrich Strecker (2011). Alexandr A. Chuprov: Life, Work, Correspondence. V&R unipress GmbH. p. 136. ISBN 978-3-89971-812-6.
- ^ a b c d Doob, Joseph (1934). "Stochastic Processes and Statistics". Proceedings of the National Academy of Sciences of the United States of America. 20 (6): 376–379. Bibcode:1934PNAS...20..376D. doi:10.1073/pnas.20.6.376. PMC 1076423. PMID 16587907.
- ^ Khintchine, A. (1934). "Korrelationstheorie der stationeren stochastischen Prozesse". Mathematische Annalen. 109 (1): 604–615. doi:10.1007/BF01449156. ISSN 0025-5831. S2CID 122842868.
- ^ Kolmogoroff, A. (1931). "Über die analytischen Methoden in der Wahrscheinlichkeitsrechnung". Mathematische Annalen. 104 (1): 1. doi:10.1007/BF01457949. ISSN 0025-5831. S2CID 119439925.
- ^ "Random". Oxford English Dictionary (Online ed.). Oxford University Press. (Subscription or participating institution membership required.)
- ^ Bert E. Fristedt; Lawrence F. Gray (2013). A Modern Approach to Probability Theory. Springer Science & Business Media. p. 580. ISBN 978-1-4899-2837-5.
- ^ a b c d L. C. G. Rogers; David Williams (2000). Diffusions, Markov Processes, and Martingales: Volume 1, Foundations. Cambridge University Press. pp. 121, 122. ISBN 978-1-107-71749-7.
- ^ a b c d e Søren Asmussen (2003). Applied Probability and Queues. Springer Science & Business Media. p. 408. ISBN 978-0-387-00211-8.
- ^ a b David Stirzaker (2005). Stochastic Processes and Models. Oxford University Press. p. 45. ISBN 978-0-19-856814-8.
- ^ Murray Rosenblatt (1962). Random Processes. Oxford University Press. p. 91.
- ^ John A. Gubner (2006). Probability and Random Processes for Electrical and Computer Engineers. Cambridge University Press. p. 383. ISBN 978-1-139-45717-0.
- ^ a b Kiyosi Itō (2006). Essentials of Stochastic Processes. American Mathematical Soc. p. 13. ISBN 978-0-8218-3898-3.
- ^ M. Loève (1978). Probability Theory II. Springer Science & Business Media. p. 163. ISBN 978-0-387-90262-3.
- ^ Pierre Brémaud (2014). Fourier Analysis and Stochastic Processes. Springer. p. 133. ISBN 978-3-319-09590-5.
- ^ a b Gusak et al. (2010), p. 1
- ^ Richard F. Bass (2011). Stochastic Processes. Cambridge University Press. p. 1. ISBN 978-1-139-50147-7.
- ^ a b ,John Lamperti (1977). Stochastic processes: a survey of the mathematical theory. Springer-Verlag. p. 3. ISBN 978-3-540-90275-1.
- ^ Fima C. Klebaner (2005). Introduction to Stochastic Calculus with Applications. Imperial College Press. p. 55. ISBN 978-1-86094-555-7.
- ^ a b Ionut Florescu (2014). Probability and Stochastic Processes. John Wiley & Sons. p. 293. ISBN 978-1-118-59320-2.
- ^ a b Florescu, Ionut (2014). Probability and Stochastic Processes. John Wiley & Sons. p. 301. ISBN 978-1-118-59320-2.
- ^ a b Bertsekas, Dimitri P.; Tsitsiklis, John N. (2002). Introduction to Probability. Athena Scientific. p. 273. ISBN 978-1-886529-40-3.
- ^ Ibe, Oliver C. (2013). Elements of Random Walk and Diffusion Processes. John Wiley & Sons. p. 11. ISBN 978-1-118-61793-9.
- ^ Achim Klenke (2013). Probability Theory: A Comprehensive Course. Springer. p. 347. ISBN 978-1-4471-5362-7.
- ^ Gregory F. Lawler; Vlada Limic (2010). Random Walk: A Modern Introduction. Cambridge University Press. p. 1. ISBN 978-1-139-48876-1.
- ^ Olav Kallenberg (2002). Foundations of Modern Probability. Springer Science & Business Media. p. 136. ISBN 978-0-387-95313-7.
- ^ Ionut Florescu (2014). Probability and Stochastic Processes. John Wiley & Sons. p. 383. ISBN 978-1-118-59320-2.
- ^ Rick Durrett (2010). Probability: Theory and Examples. Cambridge University Press. p. 277. ISBN 978-1-139-49113-6.
- ^ a b c Weiss, George H. (2006). "Random Walks". Encyclopedia of Statistical Sciences. p. 1. doi:10.1002/0471667196.ess2180.pub2. ISBN 978-0471667193.
- ^ Aris Spanos (1999). Probability Theory and Statistical Inference: Econometric Modeling with Observational Data. Cambridge University Press. p. 454. ISBN 978-0-521-42408-0.
- ^ a b Fima C. Klebaner (2005). Introduction to Stochastic Calculus with Applications. Imperial College Press. p. 81. ISBN 978-1-86094-555-7.
- ^ Allan Gut (2012). Probability: A Graduate Course. Springer Science & Business Media. p. 88. ISBN 978-1-4614-4708-5.
- ^ Geoffrey Grimmett; David Stirzaker (2001). Probability and Random Processes. OUP Oxford. p. 71. ISBN 978-0-19-857222-0.
- ^ Fima C. Klebaner (2005). Introduction to Stochastic Calculus with Applications. Imperial College Press. p. 56. ISBN 978-1-86094-555-7.
- ^ Brush, Stephen G. (1968). "A history of random processes". Archive for History of Exact Sciences. 5 (1): 1–2. doi:10.1007/BF00328110. ISSN 0003-9519. S2CID 117623580.
- ^ Applebaum, David (2004). "Lévy processes: From probability to finance and quantum groups". Notices of the AMS. 51 (11): 1338.
- ^ Iosif Ilyich Gikhman; Anatoly Vladimirovich Skorokhod (1969). Introduction to the Theory of Random Processes. Courier Corporation. p. 21. ISBN 978-0-486-69387-3.
- ^ Ionut Florescu (2014). Probability and Stochastic Processes. John Wiley & Sons. p. 471. ISBN 978-1-118-59320-2.
- ^ a b Samuel Karlin; Howard E. Taylor (2012). A First Course in Stochastic Processes. Academic Press. pp. 21, 22. ISBN 978-0-08-057041-9.
- ^ Ioannis Karatzas; Steven Shreve (1991). Brownian Motion and Stochastic Calculus. Springer. p. VIII. ISBN 978-1-4612-0949-2.
- ^ Daniel Revuz; Marc Yor (2013). Continuous Martingales and Brownian Motion. Springer Science & Business Media. p. IX. ISBN 978-3-662-06400-9.
- ^ Jeffrey S Rosenthal (2006). A First Look at Rigorous Probability Theory. World Scientific Publishing Co Inc. p. 186. ISBN 978-981-310-165-4.
- ^ Donald L. Snyder; Michael I. Miller (2012). Random Point Processes in Time and Space. Springer Science & Business Media. p. 33. ISBN 978-1-4612-3166-0.
- ^ J. Michael Steele (2012). Stochastic Calculus and Financial Applications. Springer Science & Business Media. p. 118. ISBN 978-1-4684-9305-4.
- ^ a b Peter Mörters; Yuval Peres (2010). Brownian Motion. Cambridge University Press. pp. 1, 3. ISBN 978-1-139-48657-6.
- ^ Ioannis Karatzas; Steven Shreve (1991). Brownian Motion and Stochastic Calculus. Springer. p. 78. ISBN 978-1-4612-0949-2.
- ^ Ioannis Karatzas; Steven Shreve (1991). Brownian Motion and Stochastic Calculus. Springer. p. 61. ISBN 978-1-4612-0949-2.
- ^ Steven E. Shreve (2004). Stochastic Calculus for Finance II: Continuous-Time Models. Springer Science & Business Media. p. 93. ISBN 978-0-387-40101-0.
- ^ Olav Kallenberg (2002). Foundations of Modern Probability. Springer Science & Business Media. pp. 225, 260. ISBN 978-0-387-95313-7.
- ^ Ioannis Karatzas; Steven Shreve (1991). Brownian Motion and Stochastic Calculus. Springer. p. 70. ISBN 978-1-4612-0949-2.
- ^ Peter Mörters; Yuval Peres (2010). Brownian Motion. Cambridge University Press. p. 131. ISBN 978-1-139-48657-6.
- ^ Fima C. Klebaner (2005). Introduction to Stochastic Calculus with Applications. Imperial College Press. ISBN 978-1-86094-555-7.
- ^ Ioannis Karatzas; Steven Shreve (1991). Brownian Motion and Stochastic Calculus. Springer. ISBN 978-1-4612-0949-2.
- ^ Applebaum, David (2004). "Lévy processes: From probability to finance and quantum groups". Notices of the AMS. 51 (11): 1341.
- ^ Samuel Karlin; Howard E. Taylor (2012). A First Course in Stochastic Processes. Academic Press. p. 340. ISBN 978-0-08-057041-9.
- ^ Fima C. Klebaner (2005). Introduction to Stochastic Calculus with Applications. Imperial College Press. p. 124. ISBN 978-1-86094-555-7.
- ^ Ioannis Karatzas; Steven Shreve (1991). Brownian Motion and Stochastic Calculus. Springer. p. 47. ISBN 978-1-4612-0949-2.
- ^ Ubbo F. Wiersema (2008). Brownian Motion Calculus. John Wiley & Sons. p. 2. ISBN 978-0-470-02171-2.
- ^ a b c Henk C. Tijms (2003). A First Course in Stochastic Models. Wiley. pp. 1, 2. ISBN 978-0-471-49881-0.
- ^ D.J. Daley; D. Vere-Jones (2006). An Introduction to the Theory of Point Processes: Volume I: Elementary Theory and Methods. Springer Science & Business Media. pp. 19–36. ISBN 978-0-387-21564-8.
- ^ Mark A. Pinsky; Samuel Karlin (2011). An Introduction to Stochastic Modeling. Academic Press. p. 241. ISBN 978-0-12-381416-6.
- ^ J. F. C. Kingman (1992). Poisson Processes. Clarendon Press. p. 38. ISBN 978-0-19-159124-2.
- ^ D.J. Daley; D. Vere-Jones (2006). An Introduction to the Theory of Point Processes: Volume I: Elementary Theory and Methods. Springer Science & Business Media. p. 19. ISBN 978-0-387-21564-8.
- ^ J. F. C. Kingman (1992). Poisson Processes. Clarendon Press. p. 22. ISBN 978-0-19-159124-2.
- ^ Samuel Karlin; Howard E. Taylor (2012). A First Course in Stochastic Processes. Academic Press. pp. 118, 119. ISBN 978-0-08-057041-9.
- ^ Leonard Kleinrock (1976). Queueing Systems: Theory. Wiley. p. 61. ISBN 978-0-471-49110-1.
- ^ Murray Rosenblatt (1962). Random Processes. Oxford University Press. p. 94.
- ^ a b Martin Haenggi (2013). Stochastic Geometry for Wireless Networks. Cambridge University Press. pp. 10, 18. ISBN 978-1-107-01469-5.
- ^ a b Sung Nok Chiu; Dietrich Stoyan; Wilfrid S. Kendall; Joseph Mecke (2013). Stochastic Geometry and Its Applications. John Wiley & Sons. pp. 41, 108. ISBN 978-1-118-65825-3.
- ^ J. F. C. Kingman (1992). Poisson Processes. Clarendon Press. p. 11. ISBN 978-0-19-159124-2.
- ^ a b Roy L. Streit (2010). Poisson Point Processes: Imaging, Tracking, and Sensing. Springer Science & Business Media. p. 1. ISBN 978-1-4419-6923-1.
- ^ J. F. C. Kingman (1992). Poisson Processes. Clarendon Press. p. v. ISBN 978-0-19-159124-2.
- ^ a b Alexander A. Borovkov (2013). Probability Theory. Springer Science & Business Media. p. 528. ISBN 978-1-4471-5201-9.
- ^ Georg Lindgren; Holger Rootzen; Maria Sandsten (2013). Stationary Stochastic Processes for Scientists and Engineers. CRC Press. p. 11. ISBN 978-1-4665-8618-5.
- ^ Aumann, Robert (December 1961). "Borel structures for function spaces". Illinois Journal of Mathematics. 5 (4). doi:10.1215/ijm/1255631584.
- ^ a b c Valeriy Skorokhod (2005). Basic Principles and Applications of Probability Theory. Springer Science & Business Media. pp. 93, 94. ISBN 978-3-540-26312-8.
- ^ Donald L. Snyder; Michael I. Miller (2012). Random Point Processes in Time and Space. Springer Science & Business Media. p. 25. ISBN 978-1-4612-3166-0.
- ^ Valeriy Skorokhod (2005). Basic Principles and Applications of Probability Theory. Springer Science & Business Media. p. 104. ISBN 978-3-540-26312-8.
- ^ Ionut Florescu (2014). Probability and Stochastic Processes. John Wiley & Sons. p. 296. ISBN 978-1-118-59320-2.
- ^ Patrick Billingsley (2008). Probability and Measure. Wiley India Pvt. Limited. p. 493. ISBN 978-81-265-1771-8.
- ^ Bernt Øksendal (2003). Stochastic Differential Equations: An Introduction with Applications. Springer Science & Business Media. p. 10. ISBN 978-3-540-04758-2.
- ^ a b c d e Peter K. Friz; Nicolas B. Victoir (2010). Multidimensional Stochastic Processes as Rough Paths: Theory and Applications. Cambridge University Press. p. 571. ISBN 978-1-139-48721-4.
- ^ Sidney I. Resnick (2013). Adventures in Stochastic Processes. Springer Science & Business Media. pp. 40–41. ISBN 978-1-4612-0387-2.
- ^ Ward Whitt (2006). Stochastic-Process Limits: An Introduction to Stochastic-Process Limits and Their Application to Queues. Springer Science & Business Media. p. 23. ISBN 978-0-387-21748-2.
- ^ David Applebaum (2004). Lévy Processes and Stochastic Calculus. Cambridge University Press. p. 4. ISBN 978-0-521-83263-2.
- ^ Daniel Revuz; Marc Yor (2013). Continuous Martingales and Brownian Motion. Springer Science & Business Media. p. 10. ISBN 978-3-662-06400-9.
- ^ L. C. G. Rogers; David Williams (2000). Diffusions, Markov Processes, and Martingales: Volume 1, Foundations. Cambridge University Press. p. 123. ISBN 978-1-107-71749-7.
- ^ a b c d John Lamperti (1977). Stochastic processes: a survey of the mathematical theory. Springer-Verlag. pp. 6 and 7. ISBN 978-3-540-90275-1.
- ^ Iosif I. Gikhman; Anatoly Vladimirovich Skorokhod (1969). Introduction to the Theory of Random Processes. Courier Corporation. p. 4. ISBN 978-0-486-69387-3.
- ^ a b c d Robert J. Adler (2010). The Geometry of Random Fields. SIAM. pp. 14, 15. ISBN 978-0-89871-693-1.
- ^ Sung Nok Chiu; Dietrich Stoyan; Wilfrid S. Kendall; Joseph Mecke (2013). Stochastic Geometry and Its Applications. John Wiley & Sons. p. 112. ISBN 978-1-118-65825-3.
- ^ a b Joseph L. Doob (1990). Stochastic processes. Wiley. pp. 94–96.
- ^ a b Ionut Florescu (2014). Probability and Stochastic Processes. John Wiley & Sons. pp. 298, 299. ISBN 978-1-118-59320-2.
- ^ Iosif Ilyich Gikhman; Anatoly Vladimirovich Skorokhod (1969). Introduction to the Theory of Random Processes. Courier Corporation. p. 8. ISBN 978-0-486-69387-3.
- ^ a b c David Williams (1991). Probability with Martingales. Cambridge University Press. pp. 93, 94. ISBN 978-0-521-40605-5.
- ^ Fima C. Klebaner (2005). Introduction to Stochastic Calculus with Applications. Imperial College Press. pp. 22–23. ISBN 978-1-86094-555-7.
- ^ Peter Mörters; Yuval Peres (2010). Brownian Motion. Cambridge University Press. p. 37. ISBN 978-1-139-48657-6.
- ^ a b L. C. G. Rogers; David Williams (2000). Diffusions, Markov Processes, and Martingales: Volume 1, Foundations. Cambridge University Press. p. 130. ISBN 978-1-107-71749-7.
- ^ Alexander A. Borovkov (2013). Probability Theory. Springer Science & Business Media. p. 530. ISBN 978-1-4471-5201-9.
- ^ Fima C. Klebaner (2005). Introduction to Stochastic Calculus with Applications. Imperial College Press. p. 48. ISBN 978-1-86094-555-7.
- ^ a b Bernt Øksendal (2003). Stochastic Differential Equations: An Introduction with Applications. Springer Science & Business Media. p. 14. ISBN 978-3-540-04758-2.
- ^ a b Ionut Florescu (2014). Probability and Stochastic Processes. John Wiley & Sons. p. 472. ISBN 978-1-118-59320-2.
- ^ Daniel Revuz; Marc Yor (2013). Continuous Martingales and Brownian Motion. Springer Science & Business Media. pp. 18–19. ISBN 978-3-662-06400-9.
- ^ David Applebaum (2004). Lévy Processes and Stochastic Calculus. Cambridge University Press. p. 20. ISBN 978-0-521-83263-2.
- ^ Hiroshi Kunita (1997). Stochastic Flows and Stochastic Differential Equations. Cambridge University Press. p. 31. ISBN 978-0-521-59925-2.
- ^ Olav Kallenberg (2002). Foundations of Modern Probability. Springer Science & Business Media. p. 35. ISBN 978-0-387-95313-7.
- ^ Monique Jeanblanc; Marc Yor; Marc Chesney (2009). Mathematical Methods for Financial Markets. Springer Science & Business Media. p. 11. ISBN 978-1-85233-376-8.
- ^ a b c d e f Kiyosi Itō (2006). Essentials of Stochastic Processes. American Mathematical Soc. pp. 32–33. ISBN 978-0-8218-3898-3.
- ^ Iosif Ilyich Gikhman; Anatoly Vladimirovich Skorokhod (1969). Introduction to the Theory of Random Processes. Courier Corporation. p. 150. ISBN 978-0-486-69387-3.
- ^ a b Petar Todorovic (2012). An Introduction to Stochastic Processes and Their Applications. Springer Science & Business Media. pp. 19–20. ISBN 978-1-4613-9742-7.
- ^ Ilya Molchanov (2005). Theory of Random Sets. Springer Science & Business Media. p. 340. ISBN 978-1-85233-892-3.
- ^ a b Patrick Billingsley (2008). Probability and Measure. Wiley India Pvt. Limited. pp. 526–527. ISBN 978-81-265-1771-8.
- ^ a b Alexander A. Borovkov (2013). Probability Theory. Springer Science & Business Media. p. 535. ISBN 978-1-4471-5201-9.
- ^ Gusak et al. (2010), p. 22
- ^ Joseph L. Doob (1990). Stochastic processes. Wiley. p. 56.
- ^ Davar Khoshnevisan (2006). Multiparameter Processes: An Introduction to Random Fields. Springer Science & Business Media. p. 155. ISBN 978-0-387-21631-7.
- ^ Lapidoth, Amos, A Foundation in Digital Communication, Cambridge University Press, 2009.
- ^ a b c Kun Il Park, Fundamentals of Probability and Stochastic Processes with Applications to Communications, Springer, 2018, 978-3-319-68074-3
- ^ a b c d Ward Whitt (2006). Stochastic-Process Limits: An Introduction to Stochastic-Process Limits and Their Application to Queues. Springer Science & Business Media. pp. 78–79. ISBN 978-0-387-21748-2.
- ^ a b Gusak et al. (2010), p. 24
- ^ a b c d Vladimir I. Bogachev (2007). Measure Theory (Volume 2). Springer Science & Business Media. p. 53. ISBN 978-3-540-34514-5.
- ^ a b c Fima C. Klebaner (2005). Introduction to Stochastic Calculus with Applications. Imperial College Press. p. 4. ISBN 978-1-86094-555-7.
- ^ a b Søren Asmussen (2003). Applied Probability and Queues. Springer Science & Business Media. p. 420. ISBN 978-0-387-00211-8.
- ^ a b c Patrick Billingsley (2013). Convergence of Probability Measures. John Wiley & Sons. p. 121. ISBN 978-1-118-62596-5.
- ^ Richard F. Bass (2011). Stochastic Processes. Cambridge University Press. p. 34. ISBN 978-1-139-50147-7.
- ^ Nicholas H. Bingham; Rüdiger Kiesel (2013). Risk-Neutral Valuation: Pricing and Hedging of Financial Derivatives. Springer Science & Business Media. p. 154. ISBN 978-1-4471-3856-3.
- ^ Alexander A. Borovkov (2013). Probability Theory. Springer Science & Business Media. p. 532. ISBN 978-1-4471-5201-9.
- ^ Davar Khoshnevisan (2006). Multiparameter Processes: An Introduction to Random Fields. Springer Science & Business Media. pp. 148–165. ISBN 978-0-387-21631-7.
- ^ Petar Todorovic (2012). An Introduction to Stochastic Processes and Their Applications. Springer Science & Business Media. p. 22. ISBN 978-1-4613-9742-7.
- ^ Ward Whitt (2006). Stochastic-Process Limits: An Introduction to Stochastic-Process Limits and Their Application to Queues. Springer Science & Business Media. p. 79. ISBN 978-0-387-21748-2.
- ^ Richard Serfozo (2009). Basics of Applied Stochastic Processes. Springer Science & Business Media. p. 2. ISBN 978-3-540-89332-5.
- ^ Y.A. Rozanov (2012). Markov Random Fields. Springer Science & Business Media. p. 58. ISBN 978-1-4613-8190-7.
- ^ Sheldon M. Ross (1996). Stochastic processes. Wiley. pp. 235, 358. ISBN 978-0-471-12062-9.
- ^ Ionut Florescu (2014). Probability and Stochastic Processes. John Wiley & Sons. pp. 373, 374. ISBN 978-1-118-59320-2.
- ^ a b Samuel Karlin; Howard E. Taylor (2012). A First Course in Stochastic Processes. Academic Press. p. 49. ISBN 978-0-08-057041-9.
- ^ a b Søren Asmussen (2003). Applied Probability and Queues. Springer Science & Business Media. p. 7. ISBN 978-0-387-00211-8.
- ^ Emanuel Parzen (2015). Stochastic Processes. Courier Dover Publications. p. 188. ISBN 978-0-486-79688-8.
- ^ Samuel Karlin; Howard E. Taylor (2012). A First Course in Stochastic Processes. Academic Press. pp. 29, 30. ISBN 978-0-08-057041-9.
- ^ John Lamperti (1977). Stochastic processes: a survey of the mathematical theory. Springer-Verlag. pp. 106–121. ISBN 978-3-540-90275-1.
- ^ Sheldon M. Ross (1996). Stochastic processes. Wiley. pp. 174, 231. ISBN 978-0-471-12062-9.
- ^ Sean Meyn; Richard L. Tweedie (2009). Markov Chains and Stochastic Stability. Cambridge University Press. p. 19. ISBN 978-0-521-73182-9.
- ^ Samuel Karlin; Howard E. Taylor (2012). A First Course in Stochastic Processes. Academic Press. p. 47. ISBN 978-0-08-057041-9.
- ^ Reuven Y. Rubinstein; Dirk P. Kroese (2011). Simulation and the Monte Carlo Method. John Wiley & Sons. p. 225. ISBN 978-1-118-21052-9.
- ^ Dani Gamerman; Hedibert F. Lopes (2006). Markov Chain Monte Carlo: Stochastic Simulation for Bayesian Inference, Second Edition. CRC Press. ISBN 978-1-58488-587-0.
- ^ Y.A. Rozanov (2012). Markov Random Fields. Springer Science & Business Media. p. 61. ISBN 978-1-4613-8190-7.
- ^ Donald L. Snyder; Michael I. Miller (2012). Random Point Processes in Time and Space. Springer Science & Business Media. p. 27. ISBN 978-1-4612-3166-0.
- ^ Pierre Bremaud (2013). Markov Chains: Gibbs Fields, Monte Carlo Simulation, and Queues. Springer Science & Business Media. p. 253. ISBN 978-1-4757-3124-8.
- ^ a b c Fima C. Klebaner (2005). Introduction to Stochastic Calculus with Applications. Imperial College Press. p. 65. ISBN 978-1-86094-555-7.
- ^ a b c Ioannis Karatzas; Steven Shreve (1991). Brownian Motion and Stochastic Calculus. Springer. p. 11. ISBN 978-1-4612-0949-2.
- ^ Joseph L. Doob (1990). Stochastic processes. Wiley. pp. 292, 293.
- ^ Gilles Pisier (2016). Martingales in Banach Spaces. Cambridge University Press. ISBN 978-1-316-67946-3.
- ^ a b J. Michael Steele (2012). Stochastic Calculus and Financial Applications. Springer Science & Business Media. pp. 12, 13. ISBN 978-1-4684-9305-4.
- ^ a b P. Hall; C. C. Heyde (2014). Martingale Limit Theory and Its Application. Elsevier Science. p. 2. ISBN 978-1-4832-6322-9.
- ^ J. Michael Steele (2012). Stochastic Calculus and Financial Applications. Springer Science & Business Media. p. 115. ISBN 978-1-4684-9305-4.
- ^ Sheldon M. Ross (1996). Stochastic processes. Wiley. p. 295. ISBN 978-0-471-12062-9.
- ^ a b J. Michael Steele (2012). Stochastic Calculus and Financial Applications. Springer Science & Business Media. p. 11. ISBN 978-1-4684-9305-4.
- ^ Olav Kallenberg (2002). Foundations of Modern Probability. Springer Science & Business Media. p. 96. ISBN 978-0-387-95313-7.
- ^ J. Michael Steele (2012). Stochastic Calculus and Financial Applications. Springer Science & Business Media. p. 371. ISBN 978-1-4684-9305-4.
- ^ J. Michael Steele (2012). Stochastic Calculus and Financial Applications. Springer Science & Business Media. p. 22. ISBN 978-1-4684-9305-4.
- ^ Geoffrey Grimmett; David Stirzaker (2001). Probability and Random Processes. OUP Oxford. p. 336. ISBN 978-0-19-857222-0.
- ^ Glasserman, Paul; Kou, Steven (2006). "A Conversation with Chris Heyde". Statistical Science. 21 (2): 292, 293. arXiv:math/0609294. Bibcode:2006math......9294G. doi:10.1214/088342306000000088. ISSN 0883-4237. S2CID 62552177.
- ^ Francois Baccelli; Pierre Bremaud (2013). Elements of Queueing Theory: Palm Martingale Calculus and Stochastic Recurrences. Springer Science & Business Media. ISBN 978-3-662-11657-9.
- ^ P. Hall; C. C. Heyde (2014). Martingale Limit Theory and Its Application. Elsevier Science. p. x. ISBN 978-1-4832-6322-9.
- ^ a b c d Jean Bertoin (1998). Lévy Processes. Cambridge University Press. p. viii. ISBN 978-0-521-64632-1.
- ^ a b c Applebaum, David (2004). "Lévy processes: From probability to finance and quantum groups". Notices of the AMS. 51 (11): 1336.
- ^ David Applebaum (2004). Lévy Processes and Stochastic Calculus. Cambridge University Press. p. 69. ISBN 978-0-521-83263-2.
- ^ Leonid Koralov; Yakov G. Sinai (2007). Theory of Probability and Random Processes. Springer Science & Business Media. p. 171. ISBN 978-3-540-68829-7.
- ^ David Applebaum (2004). Lévy Processes and Stochastic Calculus. Cambridge University Press. p. 19. ISBN 978-0-521-83263-2.
- ^ Sung Nok Chiu; Dietrich Stoyan; Wilfrid S. Kendall; Joseph Mecke (2013). Stochastic Geometry and Its Applications. John Wiley & Sons. p. 109. ISBN 978-1-118-65825-3.
- ^ Sung Nok Chiu; Dietrich Stoyan; Wilfrid S. Kendall; Joseph Mecke (2013). Stochastic Geometry and Its Applications. John Wiley & Sons. p. 108. ISBN 978-1-118-65825-3.
- ^ Martin Haenggi (2013). Stochastic Geometry for Wireless Networks. Cambridge University Press. p. 10. ISBN 978-1-107-01469-5.
- ^ D.J. Daley; D. Vere-Jones (2006). An Introduction to the Theory of Point Processes: Volume I: Elementary Theory and Methods. Springer Science & Business Media. p. 194. ISBN 978-0-387-21564-8.
- ^ a b c Cox, D. R.; Isham, Valerie (1980). Point Processes. CRC Press. p. 3. ISBN 978-0-412-21910-8.
- ^ J. F. C. Kingman (1992). Poisson Processes. Clarendon Press. p. 8. ISBN 978-0-19-159124-2.
- ^ Jesper Moller; Rasmus Plenge Waagepetersen (2003). Statistical Inference and Simulation for Spatial Point Processes. CRC Press. p. 7. ISBN 978-0-203-49693-0.
- ^ Samuel Karlin; Howard E. Taylor (2012). A First Course in Stochastic Processes. Academic Press. p. 31. ISBN 978-0-08-057041-9.
- ^ Volker Schmidt (2014). Stochastic Geometry, Spatial Statistics and Random Fields: Models and Algorithms. Springer. p. 99. ISBN 978-3-319-10064-7.
- ^ D.J. Daley; D. Vere-Jones (2006). An Introduction to the Theory of Point Processes: Volume I: Elementary Theory and Methods. Springer Science & Business Media. ISBN 978-0-387-21564-8.
- ^ a b c d e f Gagniuc, Paul A. (2017). Markov Chains: From Theory to Implementation and Experimentation. US: John Wiley & Sons. pp. 1–2. ISBN 978-1-119-38755-8.
- ^ David, F. N. (1955). "Studies in the History of Probability and Statistics I. Dicing and Gaming (A Note on the History of Probability)". Biometrika. 42 (1/2): 1–15. doi:10.2307/2333419. ISSN 0006-3444. JSTOR 2333419.
- ^ L. E. Maistrov (2014). Probability Theory: A Historical Sketch. Elsevier Science. p. 1. ISBN 978-1-4832-1863-2.
- ^ a b Seneta, E. (2006). "Probability, History of". Encyclopedia of Statistical Sciences. p. 1. doi:10.1002/0471667196.ess2065.pub2. ISBN 978-0471667193.
- ^ John Tabak (2014). Probability and Statistics: The Science of Uncertainty. Infobase Publishing. pp. 24–26. ISBN 978-0-8160-6873-9.
- ^ Bellhouse, David (2005). "Decoding Cardano's Liber de Ludo Aleae". Historia Mathematica. 32 (2): 180–202. doi:10.1016/j.hm.2004.04.001. ISSN 0315-0860.
- ^ Anders Hald (2005). A History of Probability and Statistics and Their Applications before 1750. John Wiley & Sons. p. 221. ISBN 978-0-471-72517-6.
- ^ L. E. Maistrov (2014). Probability Theory: A Historical Sketch. Elsevier Science. p. 56. ISBN 978-1-4832-1863-2.
- ^ John Tabak (2014). Probability and Statistics: The Science of Uncertainty. Infobase Publishing. p. 37. ISBN 978-0-8160-6873-9.
- ^ a b Chung, Kai Lai (1998). "Probability and Doob". The American Mathematical Monthly. 105 (1): 28–35. doi:10.2307/2589523. ISSN 0002-9890. JSTOR 2589523.
- ^ a b c d e f Bingham, N. (2000). "Studies in the history of probability and statistics XLVI. Measure into probability: from Lebesgue to Kolmogorov". Biometrika. 87 (1): 145–156. doi:10.1093/biomet/87.1.145. ISSN 0006-3444.
- ^ a b Benzi, Margherita; Benzi, Michele; Seneta, Eugene (2007). "Francesco Paolo Cantelli. b. 20 December 1875 d. 21 July 1966". International Statistical Review. 75 (2): 128. doi:10.1111/j.1751-5823.2007.00009.x. ISSN 0306-7734. S2CID 118011380.
- ^ Doob, Joseph L. (1996). "The Development of Rigor in Mathematical Probability (1900-1950)". The American Mathematical Monthly. 103 (7): 586–595. doi:10.2307/2974673. ISSN 0002-9890. JSTOR 2974673.
- ^ a b c d e f g h i j Cramer, Harald (1976). "Half a Century with Probability Theory: Some Personal Recollections". The Annals of Probability. 4 (4): 509–546. doi:10.1214/aop/1176996025. ISSN 0091-1798.
- ^ Truesdell, C. (1975). "Early kinetic theories of gases". Archive for History of Exact Sciences. 15 (1): 22–23. doi:10.1007/BF00327232. ISSN 0003-9519. S2CID 189764116.
- ^ Brush, Stephen G. (1967). "Foundations of statistical mechanics 1845?1915". Archive for History of Exact Sciences. 4 (3): 150–151. doi:10.1007/BF00412958. ISSN 0003-9519. S2CID 120059181.
- ^ Truesdell, C. (1975). "Early kinetic theories of gases". Archive for History of Exact Sciences. 15 (1): 31–32. doi:10.1007/BF00327232. ISSN 0003-9519. S2CID 189764116.
- ^ Brush, S.G. (1958). "The development of the kinetic theory of gases IV. Maxwell". Annals of Science. 14 (4): 243–255. doi:10.1080/00033795800200147. ISSN 0003-3790.
- ^ Brush, Stephen G. (1968). "A history of random processes". Archive for History of Exact Sciences. 5 (1): 15–16. doi:10.1007/BF00328110. ISSN 0003-9519. S2CID 117623580.
- ^ a b c d Kendall, D. G.; Batchelor, G. K.; Bingham, N. H.; Hayman, W. K.; Hyland, J. M. E.; Lorentz, G. G.; Moffatt, H. K.; Parry, W.; Razborov, A. A.; Robinson, C. A.; Whittle, P. (1990). "Andrei Nikolaevich Kolmogorov (1903–1987)". Bulletin of the London Mathematical Society. 22 (1): 33. doi:10.1112/blms/22.1.31. ISSN 0024-6093.
- ^ Vere-Jones, David (2006). "Khinchin, Aleksandr Yakovlevich". Encyclopedia of Statistical Sciences. p. 1. doi:10.1002/0471667196.ess6027.pub2. ISBN 978-0471667193.
- ^ a b Vere-Jones, David (2006). "Khinchin, Aleksandr Yakovlevich". Encyclopedia of Statistical Sciences. p. 4. doi:10.1002/0471667196.ess6027.pub2. ISBN 978-0471667193.
- ^ a b Snell, J. Laurie (2005). "Obituary: Joseph Leonard Doob". Journal of Applied Probability. 42 (1): 251. doi:10.1239/jap/1110381384. ISSN 0021-9002.
- ^ Lindvall, Torgny (1991). "W. Doeblin, 1915-1940". The Annals of Probability. 19 (3): 929–934. doi:10.1214/aop/1176990329. ISSN 0091-1798.
- ^ a b c Getoor, Ronald (2009). "J. L. Doob: Foundations of stochastic processes and probabilistic potential theory". The Annals of Probability. 37 (5): 1655. arXiv:0909.4213. Bibcode:2009arXiv0909.4213G. doi:10.1214/09-AOP465. ISSN 0091-1798. S2CID 17288507.
- ^ a b Bingham, N. H. (2005). "Doob: a half-century on". Journal of Applied Probability. 42 (1): 257–266. doi:10.1239/jap/1110381385. ISSN 0021-9002.
- ^ a b c d e Meyer, Paul-André (2009). "Stochastic Processes from 1950 to the Present". Electronic Journal for History of Probability and Statistics. 5 (1): 1–42.
- ^ "Kiyosi Itô receives Kyoto Prize". Notices of the AMS. 45 (8): 981–982. 1998.
- ^ Jean Bertoin (1998). Lévy Processes. Cambridge University Press. p. viii and ix. ISBN 978-0-521-64632-1.
- ^ J. Michael Steele (2012). Stochastic Calculus and Financial Applications. Springer Science & Business Media. p. 176. ISBN 978-1-4684-9305-4.
- ^ P. Hall; C. C. Heyde (2014). Martingale Limit Theory and Its Application. Elsevier Science. pp. 1, 2. ISBN 978-1-4832-6322-9.
- ^ Dynkin, E. B. (1989). "Kolmogorov and the Theory of Markov Processes". The Annals of Probability. 17 (3): 822–832. doi:10.1214/aop/1176991248. ISSN 0091-1798.
- ^ Ellis, Richard S. (1995). "An overview of the theory of large deviations and applications to statistical mechanics". Scandinavian Actuarial Journal. 1995 (1): 98. doi:10.1080/03461238.1995.10413952. ISSN 0346-1238.
- ^ Raussen, Martin; Skau, Christian (2008). "Interview with Srinivasa Varadhan". Notices of the AMS. 55 (2): 238–246.
- ^ Malte Henkel; Dragi Karevski (2012). Conformal Invariance: an Introduction to Loops, Interfaces and Stochastic Loewner Evolution. Springer Science & Business Media. p. 113. ISBN 978-3-642-27933-1.
- ^ "2006 Fields Medals Awarded". Notices of the AMS. 53 (9): 1041–1044. 2015.
- ^ Quastel, Jeremy (2015). "The Work of the 2014 Fields Medalists". Notices of the AMS. 62 (11): 1341–1344.
- ^ D.J. Daley; D. Vere-Jones (2006). An Introduction to the Theory of Point Processes: Volume I: Elementary Theory and Methods. Springer Science & Business Media. pp. 1–4. ISBN 978-0-387-21564-8.
- ^ Anders Hald (2005). A History of Probability and Statistics and Their Applications before 1750. John Wiley & Sons. p. 226. ISBN 978-0-471-72517-6.
- ^ a b Joel Louis Lebowitz (1984). Nonequilibrium phenomena II: from stochastics to hydrodynamics. North-Holland Pub. pp. 8–10. ISBN 978-0-444-86806-0.
- ^ Ionut Florescu (2014). Probability and Stochastic Processes. John Wiley & Sons. p. 374. ISBN 978-1-118-59320-2.
- ^ Oliver C. Ibe (2013). Elements of Random Walk and Diffusion Processes. John Wiley & Sons. p. 5. ISBN 978-1-118-61793-9.
- ^ Anders Hald (2005). A History of Probability and Statistics and Their Applications before 1750. John Wiley & Sons. p. 63. ISBN 978-0-471-72517-6.
- ^ Anders Hald (2005). A History of Probability and Statistics and Their Applications before 1750. John Wiley & Sons. p. 202. ISBN 978-0-471-72517-6.
- ^ Ionut Florescu (2014). Probability and Stochastic Processes. John Wiley & Sons. p. 385. ISBN 978-1-118-59320-2.
- ^ Barry D. Hughes (1995). Random Walks and Random Environments: Random walks. Clarendon Press. p. 111. ISBN 978-0-19-853788-5.
- ^ Thiele, Thorwald N. (1880). "Om Anvendelse af mindste Kvadraterbs Methode i nogle Tilfælde, hvoren Komplikation af visse Slags uensartede tilfældige Fejlkilder giver Fejleneen "systematisk" Karakter". Kongelige Danske Videnskabernes Selskabs Skrifter. Series 5 (12): 381–408.
- ^ Hald, Anders (1981). "T. N. Thiele's Contributions to Statistics". International Statistical Review / Revue Internationale de Statistique. 49 (1): 1–20. doi:10.2307/1403034. ISSN 0306-7734. JSTOR 1403034.
- ^ a b Lauritzen, Steffen L. (1981). "Time Series Analysis in 1880: A Discussion of Contributions Made by T.N. Thiele". International Statistical Review / Revue Internationale de Statistique. 49 (3): 319–320. doi:10.2307/1402616. ISSN 0306-7734. JSTOR 1402616.
- ^ Bachelier, Luis (1900). "Théorie de la spéculation" (PDF). Ann. Sci. Éc. Norm. Supér. Serie 3, 17: 21–89. doi:10.24033/asens.476.
- ^ Bachelier, Luis (1900). "The Theory of Speculation". Ann. Sci. Éc. Norm. Supér. Serie 3, 17: 21–89 (Engl. translation by David R. May, 2011). doi:10.24033/asens.476.
- ^ a b Courtault, Jean-Michel; Kabanov, Yuri; Bru, Bernard; Crepel, Pierre; Lebon, Isabelle; Le Marchand, Arnaud (2000). "Louis Bachelier on the Centenary of Theorie de la Speculation" (PDF). Mathematical Finance. 10 (3): 339–353. doi:10.1111/1467-9965.00098. ISSN 0960-1627. S2CID 14422885.
- ^ a b c d e Jovanovic, Franck (2012). "Bachelier: Not the forgotten forerunner he has been depicted as. An analysis of the dissemination of Louis Bachelier's work in economics" (PDF). The European Journal of the History of Economic Thought. 19 (3): 431–451. doi:10.1080/09672567.2010.540343. ISSN 0967-2567. S2CID 154003579.
- ^ Brush, Stephen G. (1968). "A history of random processes". Archive for History of Exact Sciences. 5 (1): 25. doi:10.1007/BF00328110. ISSN 0003-9519. S2CID 117623580.
- ^ Brush, Stephen G. (1968). "A history of random processes". Archive for History of Exact Sciences. 5 (1): 1–36. doi:10.1007/BF00328110. ISSN 0003-9519. S2CID 117623580.
- ^ D.J. Daley; D. Vere-Jones (2006). An Introduction to the Theory of Point Processes: Volume I: Elementary Theory and Methods. Springer Science & Business Media. pp. 8–9. ISBN 978-0-387-21564-8.
- ^ Embrechts, Paul; Frey, Rüdiger; Furrer, Hansjörg (2001). "Stochastic processes in insurance and finance". Stochastic Processes: Theory and Methods. Handbook of Statistics. Vol. 19. p. 367. doi:10.1016/S0169-7161(01)19014-0. ISBN 978-0444500144. ISSN 0169-7161.
- ^ Cramér, Harald (1969). "Historical review of Filip Lundberg's works on risk theory". Scandinavian Actuarial Journal. 1969 (sup3): 6–12. doi:10.1080/03461238.1969.10404602. ISSN 0346-1238.
- ^ a b Gagniuc, Paul A. (2017). Markov Chains: From Theory to Implementation and Experimentation. NJ: John Wiley & Sons. pp. 2–8. ISBN 978-1-119-38755-8.
- ^ a b Gagniuc, Paul A. (2017). Markov Chains: From Theory to Implementation and Experimentation. NJ: John Wiley & Sons. pp. 1–235. ISBN 978-1-119-38755-8.
- ^ a b c d Charles Miller Grinstead; James Laurie Snell (1997). Introduction to Probability. American Mathematical Soc. pp. 464–466. ISBN 978-0-8218-0749-1.
- ^ a b Pierre Bremaud (2013). Markov Chains: Gibbs Fields, Monte Carlo Simulation, and Queues. Springer Science & Business Media. p. ix. ISBN 978-1-4757-3124-8.
- ^ a b Hayes, Brian (2013). "First links in the Markov chain". American Scientist. 101 (2): 92–96. doi:10.1511/2013.101.92.
- ^ Seneta, E. (1998). "I.J. Bienaymé [1796-1878]: Criticality, Inequality, and Internationalization". International Statistical Review / Revue Internationale de Statistique. 66 (3): 291–292. doi:10.2307/1403518. ISSN 0306-7734. JSTOR 1403518.
- ^ Bru, B.; Hertz, S. (2001). "Maurice Fréchet". Statisticians of the Centuries. pp. 331–334. doi:10.1007/978-1-4613-0179-0_71. ISBN 978-0-387-95283-3.
- ^ Marc Barbut; Bernard Locker; Laurent Mazliak (2016). Paul Lévy and Maurice Fréchet: 50 Years of Correspondence in 107 Letters. Springer London. p. 5. ISBN 978-1-4471-7262-8.
- ^ Valeriy Skorokhod (2005). Basic Principles and Applications of Probability Theory. Springer Science & Business Media. p. 146. ISBN 978-3-540-26312-8.
- ^ Bernstein, Jeremy (2005). "Bachelier". American Journal of Physics. 73 (5): 398–396. Bibcode:2005AmJPh..73..395B. doi:10.1119/1.1848117. ISSN 0002-9505.
- ^ William J. Anderson (2012). Continuous-Time Markov Chains: An Applications-Oriented Approach. Springer Science & Business Media. p. vii. ISBN 978-1-4612-3038-0.
- ^ Kendall, D. G.; Batchelor, G. K.; Bingham, N. H.; Hayman, W. K.; Hyland, J. M. E.; Lorentz, G. G.; Moffatt, H. K.; Parry, W.; Razborov, A. A.; Robinson, C. A.; Whittle, P. (1990). "Andrei Nikolaevich Kolmogorov (1903–1987)". Bulletin of the London Mathematical Society. 22 (1): 57. doi:10.1112/blms/22.1.31. ISSN 0024-6093.
- ^ David Applebaum (2004). Lévy Processes and Stochastic Calculus. Cambridge University Press. p. 67. ISBN 978-0-521-83263-2.
- ^ a b c Robert J. Adler (2010). The Geometry of Random Fields. SIAM. p. 13. ISBN 978-0-89871-693-1.
- ^ Krishna B. Athreya; Soumendra N. Lahiri (2006). Measure Theory and Probability Theory. Springer Science & Business Media. ISBN 978-0-387-32903-1.
- ^ Bernt Øksendal (2003). Stochastic Differential Equations: An Introduction with Applications. Springer Science & Business Media. p. 11. ISBN 978-3-540-04758-2.
- ^ David Williams (1991). Probability with Martingales. Cambridge University Press. p. 124. ISBN 978-0-521-40605-5.
- ^ Rick Durrett (2010). Probability: Theory and Examples. Cambridge University Press. p. 410. ISBN 978-1-139-49113-6.
- ^ Patrick Billingsley (2008). Probability and Measure. Wiley India Pvt. Limited. pp. 493–494. ISBN 978-81-265-1771-8.
- ^ Alexander A. Borovkov (2013). Probability Theory. Springer Science & Business Media. pp. 529–530. ISBN 978-1-4471-5201-9.
- ^ Krishna B. Athreya; Soumendra N. Lahiri (2006). Measure Theory and Probability Theory. Springer Science & Business Media. p. 221. ISBN 978-0-387-32903-1.
- ^ a b Robert J. Adler; Jonathan E. Taylor (2009). Random Fields and Geometry. Springer Science & Business Media. p. 14. ISBN 978-0-387-48116-6.
- ^ Krishna B. Athreya; Soumendra N. Lahiri (2006). Measure Theory and Probability Theory. Springer Science & Business Media. p. 211. ISBN 978-0-387-32903-1.
- ^ Alexander A. Borovkov (2013). Probability Theory. Springer Science & Business Media. p. 536. ISBN 978-1-4471-5201-9.
- ^ Benjamin Yakir (2013). Extremes in Random Fields: A Theory and Its Applications. John Wiley & Sons. p. 5. ISBN 978-1-118-72062-2.
Further reading
This further reading section may contain inappropriate or excessive suggestions that may not follow Wikipedia's guidelines. Please ensure that only a reasonable number of balanced, topical, reliable, and notable further reading suggestions are given; removing less relevant or redundant publications with the same point of view where appropriate. Consider utilising appropriate texts as inline sources or creating a separate bibliography article. (July 2018) |
Articles
- Applebaum, David (2004). "Lévy processes: From probability to finance and quantum groups". Notices of the AMS. 51 (11): 1336–1347.
- Cramer, Harald (1976). "Half a Century with Probability Theory: Some Personal Recollections". The Annals of Probability. 4 (4): 509–546. doi:10.1214/aop/1176996025. ISSN 0091-1798.
- Guttorp, Peter; Thorarinsdottir, Thordis L. (2012). "What Happened to Discrete Chaos, the Quenouille Process, and the Sharp Markov Property? Some History of Stochastic Point Processes". International Statistical Review. 80 (2): 253–268. doi:10.1111/j.1751-5823.2012.00181.x. ISSN 0306-7734. S2CID 80836.
- Jarrow, Robert; Protter, Philip (2004). "A short history of stochastic integration and mathematical finance: the early years, 1880–1970". A Festschrift for Herman Rubin. Institute of Mathematical Statistics Lecture Notes - Monograph Series. pp. 75–91. doi:10.1214/lnms/1196285381. ISBN 978-0-940600-61-4. ISSN 0749-2170.
- Meyer, Paul-André (2009). "Stochastic Processes from 1950 to the Present". Electronic Journal for History of Probability and Statistics. 5 (1): 1–42.
Books
- Robert J. Adler (2010). The Geometry of Random Fields. SIAM. ISBN 978-0-89871-693-1.
- Robert J. Adler; Jonathan E. Taylor (2009). Random Fields and Geometry. Springer Science & Business Media. ISBN 978-0-387-48116-6.
- Pierre Brémaud (2013). Markov Chains: Gibbs Fields, Monte Carlo Simulation, and Queues. Springer Science & Business Media. ISBN 978-1-4757-3124-8.
- Joseph L. Doob (1990). Stochastic processes. Wiley.
- Anders Hald (2005). A History of Probability and Statistics and Their Applications before 1750. John Wiley & Sons. ISBN 978-0-471-72517-6.
- Crispin Gardiner (2010). Stochastic Methods. Springer. ISBN 978-3-540-70712-7.
- Iosif I. Gikhman; Anatoly Vladimirovich Skorokhod (1996). Introduction to the Theory of Random Processes. Courier Corporation. ISBN 978-0-486-69387-3.
- Emanuel Parzen (2015). Stochastic Processes. Courier Dover Publications. ISBN 978-0-486-79688-8.
- Murray Rosenblatt (1962). Random Processes. Oxford University Press.
External links
 Media related to Stochastic processes at Wikimedia Commons
Media related to Stochastic processes at Wikimedia Commons


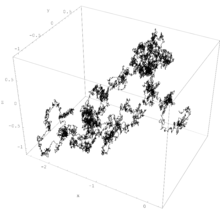


 확률
확률 









 \
\


















 함수 구성을
함수 구성을 

 대해 X
대해 X





 대해
대해




 의존합니다.
의존합니다.

 동일한 색인
동일한 색인  갖는 확률
갖는 확률 











![{\displaystyle \operatorname {K} _{\mathbf {X} \mathbf {Y} }(t_{1},t_{2})=\operatorname {E} \left[\left(X(t_{1})-\mu _{X}(t_{1})\right)\left(Y(t_{2})-\mu _{Y}(t_{2})\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0bf123985d84cdc25587546891caea6d23dc4f6d)

![{\displaystyle \operatorname {R} _{\mathbf {X} \mathbf {Y} }(t_{1},t_{2})=\operatorname {E} [X(t_{1}){\overline {Y(t_{2})}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93d58e51ab83745d727396e86c894660ee44857e)

![[0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)


![{\displaystyle D[0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4d18229131d1ad9cd7cff586ad63243aa6acaae)








