마르코프 체인

통계에 대한 시리즈 일부
확률론
확률 공리 결정론 시스템 인디테르민주의 무작위성
확률공간 샘플 공간 이벤트 총체적으로 철저한 사건들 초등 이벤트 상호배타성 결과 싱글턴 실험 베르누이 재판 확률분포 베르누이 분포 이항 분포 정규 분포 확률측도 변량변수 베르누이 과정 연속 또는 이산형 기대값 마르코프 체인 관측치 무작위 보행 확률적 과정
보완적 사건 관절확률 한계 확률 조건부 확률
독립 조건부 독립성 전체 확률의 법칙 대수의 법칙 베이즈 정리 부울의 부등식
벤 다이어그램 트리 다이어그램
v t

마르코프 체인 또는 마르코프 프로세스는 각 사건의 확률이 이전 사건에서 획득한 상태에만 의존하는 가능한 사건의 순서를 설명하는 확률적 모델이다.^[1][2][3]체인이 개별 시간 단계에서 상태를 이동하는 카운트할 수 있는 무한 시퀀스는 이산 시간 마코프 체인(DTMC)을 제공한다.연속 시간 프로세스는 연속 시간 마코프 체인(CTMC)이라고 불린다.러시아의 수학자 안드레이 마르코프의 이름을 따서 지은 것이다.

마르코프 체인은 자동차의 크루즈 컨트롤 시스템 연구, 공항에 도착하는 대기열 또는 줄의 고객 연구,^[1][4][5][6] 환율 및 동물 인구 역학 등 실제 프로세스의 통계적 모델로서 많은 응용 프로그램을 가지고 있다.^[7]

마르코프 공정은 복잡한 확률분포에서 추출한 표본을 시뮬레이션하는 데 사용되는 마르코프 체인 몬테카를로라고 알려진 일반적인 확률적 시뮬레이션 방법의 기초로서 베이시안 통계, 열역학, 통계역학, 물리학, 화학, 경제, 금융, 신호처리, 정보에서 응용을 찾아냈다.어리와 언어 ^[7][8][9]처리

형용사 마르코비안과 마르코프는 마르코프 과정과 관련된 것을 묘사할 때 사용된다.^[1][10][11]

소개

정의

마르코프 과정은 마르코프 속성^[1](때로는 "메모리 없는 상태"로 특징지어짐)을 만족시키는 확률적인 과정이다.간단히 말해서, 그것은 단지 현재 상태에 기초하여 미래 결과에 대해 예측이 이루어질 수 있는 과정이며, 가장 중요한 것은 그러한 예측이 프로세스의 전체 이력을 알면서 이루어질 수 있는 예측과 같다.^[12]즉, 제도의 현재 상태, 그것의 미래, 과거의 상태를 조건으로 하여 독립적이다.

마르코프 체인은 마르코프 프로세스의 일종으로, 분리된 상태 공간이나 이산 인덱스 세트(흔히 시간을 나타냄)^[13]를 가지고 있지만, 마르코프 체인의 정확한 정의는 다양하다.예를 들어 그것은 가산 명사의 상태 공간(따라서 관계 없이 시간의 본질에)[14][15][16][17]을 별개 또는 연속적인 시간에 마르코프 과정은 마르코프 연쇄를 정의하라 또는 연속 계수 상태 공간(따라서 관계 없이 상태 공간의)에 분산적인 시간을 보내고는 마르코프 연쇄를 정의하는 것은 흔한 일 흔하다.[13]

마르코프 체인의 종류

시스템의 상태 공간 및 시간 매개변수 지수를 지정해야 한다.다음 표에는 다양한 수준의 상태 공간 일반성과 이산 시간 v. 연속 시간에 대한 마르코프 프로세스의 여러 인스턴스(instance)에 대한 개요가 나와 있다.

	카운트 가능한 상태 공간	연속 또는 일반 상태 공간
이산 시간	(구체-시간) 카운트 가능 또는 유한 상태 공간의 마르코프 체인	측정 가능한 상태 공간의 마르코프 체인(예: 해리스 체인)
연속시간	연속 시간 Markov 프로세스 또는 Markov 점프 프로세스	마르코프 속성을 가진 모든 연속 확률적 프로세스(예: Wiener 프로세스)

마르코프 프로세스의 특수한 경우를 나타내는 일부 용어의 사용에 대한 문헌에는 명확한 합의가 없다는 점에 유의한다.일반적으로 "마코프 체인"이라는 용어는 이산 시간 마코프 체인(DTMC)이라는 시간을 가진 공정을 위해 예약되어 있지만,^[1][18] 소수의 저자는 명시적인 언급 없이 연속 시간 마코프 체인(CTMC)을 지칭하기 위해 "마코프 프로세스"라는 용어를 사용한다.^[19][20][21]또한 마르코프 프로세스에는 이와 같이 언급되지만 반드시 이 네 가지 범주 중 어느 하나에 속하지는 않는 다른 확장도 있다(마코프 모델 참조).게다가, 시간 지수를 반드시 실제 가치로 평가할 필요는 없다; 주 공간과 마찬가지로, 다른 수학 구조와 함께 인덱스 세트를 통해 이동하는 상상할 수 있는 과정들이 있다.일반 주 공간 연속 시간 마코프 체인은 지정된 용어가 없을 정도로 일반적이라는 점에 유의하십시오.

시간 매개변수는 보통 이산형이지만, 마르코프 체인의 상태 공간에는 일반적으로 합의된 제한이 없다. 이 용어는 임의의 상태 공간에 대한 과정을 나타낼 수 있다.^[22]그러나 마르코프 체인의 많은 애플리케이션은 유한하거나 헤아릴 수 없을 정도로 무한한 상태 공간을 채용하고 있는데, 이것은 통계 분석이 더 간단하다.시간 인덱스 및 상태 공간 매개변수 외에도 많은 다른 변형, 확장 및 일반화가 있다(변형 참조).간단히 말해서, 이 글의 대부분은 별개의 시간, 별개의 주-공간 사례에 초점을 맞추고 있다.

전환

시스템의 상태 변화를 전환이라고 한다.^[1]다양한 상태 변화와 관련된 확률을 전환 확률이라고 한다.프로세스는 상태 공간, 특정 전환의 확률을 설명하는 전환 매트릭스 및 상태 공간에 걸친 초기 상태(또는 초기 분포)로 특징지어진다.관례에 따라 가능한 모든 상태와 전환이 프로세스의 정의에 포함되었기 때문에 항상 다음 상태가 존재하며 프로세스가 종료되지 않는다고 가정한다.

이산 시간 무작위 프로세스는 각 단계에서 특정 상태에 있는 시스템을 포함하며, 단계 간에 상태가 무작위로 변경된다.^[1]이 단계는 흔히 시간의 순간으로 생각되지만, 물리적 거리나 다른 이산적 측정을 똑같이 잘 나타낼 수 있다.형식적으로 단계는 정수 또는 자연수이며, 무작위 과정은 이들을 상태에 매핑하는 것이다.^[23]마르코프 속성은 다음 단계(사실상 모든 미래 단계)에서 시스템에 대한 조건부 확률 분포는 시스템의 현재 상태에 따라서만 달라지며, 이전 단계에서는 시스템 상태에 추가로 의존하지 않는다고 명시하고 있다.

시스템이 무작위로 변화하기 때문에, 일반적으로 미래의 특정 시점에서 마르코프 체인의 상태를 확실하게 예측하는 것은 불가능하다.^[23]그러나 시스템 미래의 통계적 특성을 예측할 수 있다.^[23]많은 응용 프로그램에서 중요한 것은 이러한 통계적 속성이다.

역사

마르코프는 1906년 이 주제에 대한 첫 논문을 발표하면서 20세기 초 마르코프 과정을 연구했다.^{[24][25][26][27]}연속 시간의 마르코프 과정은 20세기^[1] 초 안드레이 마르코프가 작업하기 훨씬 전에 포아송 공정의 형태로 발견되었다.^[28][29][30]마르코프는 많은 수의 약한 법칙이 유지되기 위해서는 독립이 필요하다고 주장한 파벨 네크라소프와의 의견 불일치로 인해 독립적인 무작위 시퀀스의 확장을 연구하는데 관심이 있었다.^[1][31]마르코프 체인에 그의 첫번째 종이, 1906년에 발표된 논문에서 마르코프가 특정 조건에서 마르코프 연쇄의 평균 결과 값의 고정된 벡터, 그러니까 흔히 이러한 수학적 la.에 대한 요건으로 여겨져 왔던 독립 assumption,[1][25][26][27]없이 큰 수의 약한 법이라고 증명되고 융합하는 것으로 나타났다그를 열 계획입니다.[27]마르코프는 이후 마르코프 체인을 이용해 알렉산더 푸시킨이 쓴 유진 오네긴의 모음 분포를 연구했고, 그러한 체인에 대한 중심적 한계 정리를 증명했다.^[1][25]

1912년 앙리 푸앵카레는 카드 섞기를 연구하기 위한 목적으로 유한한 그룹의 마르코프 체인을 연구했다.마르코프 체인의 다른 초기 사용으로는 1907년 바울과 타티아나 에렌페스트가 도입한 확산 모델과 마르코프의 작업에 앞서 1873년 프랜시스 갈튼과 헨리 윌리엄 왓슨이 도입한 분기 과정이 있다.^[25][26]갈튼과 왓슨의 작업 후, 그들의 분기 과정이 약 30년 전에 이리네-줄스 비에나이메에 의해 독자적으로 발견되고 연구되었다는 것이 나중에 밝혀졌다.^[32]1928년부터 모리스 프레셰트는 마르코프 체인에 관심을 갖게 되었고, 결국 1938년에 마르코프 체인에 대한 상세한 연구를 출판하게 되었다.^[25][33]

안드레이 콜모고로프는 1931년 논문에서 연속시간 마르코프 과정의 초기 이론의 상당 부분을 발전시켰다.^[34][35]콜모고로프는 1900년 루이스 바첼리에의 주식시장 변동에 관한 연구뿐만 아니라 노르베르트 비에너가 아인슈타인의 브라운 운동 모델에 관한 연구에서도 부분적으로 영감을 받았다.^[34][36]그는 확산 과정으로 알려진 마르코프 과정의 특정 집합을 소개하고 연구했는데, 여기서 그는 그 과정을 설명하는 일련의 미분 방정식을 도출했다.^[34][37]콜모고로프의 연구와는 별개로, 시드니 채프먼은 1928년 논문에서 브라운 운동을 연구하면서 콜모고로프보다 수학적으로 덜 엄격한 방법으로 현재 채프만-콜모고로프 방정식이라고 불리는 방정식을 도출했다.^[38]미분 방정식은 현재 콜모고로프 방정식^[39] 또는 콜모고로프-차프만 방정식이라고 불린다.^[40]마르코프 과정의 기초에 크게 기여한 다른 수학자들로는 1930년대부터 윌리엄 펠러(William Feller), 1950년대부터는 유진 딘킨(Eugene Dynkin)이 있다.^[35]

예

정수를 바탕으로 한 무작위 산책과 도박꾼의 파멸 문제가 마르코프 과정의 예다.^[41][42]이러한 프로세스의 일부 변동은 독립 변수의 맥락에서 수백 년 전에 연구되었다.^[43][44][45]마르코프 과정의 두 가지 중요한 예는 브라운 운동 과정이라고도 알려진 위너 과정과 포아송 과정으로,^[28] 확률적 과정 이론에서 가장 중요하고 중심적인 확률적 과정으로 간주된다.^[46][47][48]이 두 과정은 연속 시간에 마르코프 과정인 반면, 정수를 무작위로 걷는 것과 도박사의 파멸 문제는 이산 시간에 마르코프 과정의 예다.^[41][42]

유명한 마르코프 체인은 소위 "드렁커드의 걸음"으로, 각 단계에서 위치가 동일한 확률로 +1 또는 -1만큼 변할 수 있는 숫자 라인에서의 무작위 걷기이다.어떤 위치에서든 다음 또는 이전 정수로의 두 가지 전환이 가능하다.전환 확률은 현재 위치에 도달한 방식에 따라 달라지지 않는다.예를 들어, 5에서 4까지의 경과 확률과 5에서 6까지의 경과 확률은 모두 0.5이며, 5에서 오는 다른 경과 확률은 모두 0이다.이러한 확률은 시스템이 이전에 4 또는 6에 있었는지와 무관하다.

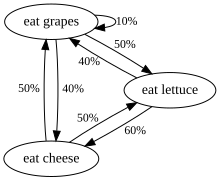
또 다른 예는 포도, 치즈, 상추만 먹고 식습관이 다음과 같은 규칙에 부합하는 생물의 식습관이다.

• 하루에 딱 한 번 먹는다.
• 만약 오늘 치즈를 먹었다면 내일은 상추나 포도를 같은 확률로 먹을 것이다.
• 오늘 포도를 먹었다면 내일은 확률 1/10의 포도, 확률 4/10의 치즈, 확률 5/10의 상추를 먹는다.
• 오늘 상추를 먹었다면 내일은 포도를 4/10 확률로 먹거나 치즈를 6/10 확률로 먹는다.그것은 내일 상추를 다시 먹지 않을 것이다.

이 생물의 식습관은 마르코프 사슬로 모형화할 수 있다. 왜냐하면 내일의 선택은 어제나 과거에 무엇을 먹었는가가 아니라 오늘 무엇을 먹었느냐에 달려 있기 때문이다.계산될 수 있는 한 가지 통계적 속성은 장기간에 걸쳐 그 생물이 포도를 먹는 날의 예상 백분율이다.

일련의 독립적인 사건(예: 일련의 동전 던지기)은 마르코프 체인의 공식 정의를 충족한다.그러나 이 이론은 보통 다음 단계의 확률 분포가 현 상태에 비독점적으로 의존하는 경우에만 적용된다.

비 마르코프 예제

5/4(각각 25㎝), 5데임(각각 10㎝), 5니켈(각각 5㎝)이 들어 있는 동전 지갑이 있고, 하나둘씩 지갑에서 동전을 무작위로 뽑아 탁자 위에 놓아둔다고 가정해 보자.$X{\displaystyle {}_{}}$ ${\displaystyle {n\mathrm{}}_{}}$ ${\$이(가) n ${\displaystyle \mathrm{그리기}}$ 후 테이블에 설정된 코인의 총 값을 X $0{\displaystyle {}_{}}$= 0 ${\displaystyle X_{0}=0$으로 나타낸다면$,{\displaystyle }$ {${\displaystyle X_{}}$ : $displaystyle${$N}}}}}}}}}}}}}}}}}}}}}}\$mathb$$.

왜 이런지를 알기 위해서, 첫 6무에서 5 니켈과 4분의 1을 모두 그렸다고 가정해보자.Thus ${\displaystyle X_{6}=\$0.50}$. If we know not just ${\displaystyle X_{6}}$, but the earlier values as well, then we can determine which coins have been drawn, and we know that the next coin will not be a nickel; so we can determine that ${\displaystyle X_{7}\geq \$0.60}$ with probab일성 1.그러나 만약 우리가 이전의 값을 알지 못한다면, $단지{\displaystyle {}_{}}$ ${\displaystyle {X\mathrm{}}_{}}$ 6$${\$displaystyle X_{6$}의 값만을 기초로 해서, 우리는$$ 4디임과 2 니켈을 그렸을 것이라고 추측할 수 있을 것이다. 그 경우 다음에 또 다른 니켈을 그리는 것은 분명히 가능할 것이다.따라서, ${\displaystyle {X\mathrm{}}_{}}$ 7$${\$displaystyle X_{7}$에 대한 우리의 추측은 X ${\displaystyle {6\mathrm{}}_{}}$ ${\$ 이전의 값에 대한 지식의 영향을 받는다$$$.$

그러나 이 시나리오를 마르코프 과정으로 모델링하는 것은 가능하다.$Xn{\displaystyle {}_{}}$ ${\$를 정의하여$$ 표에 있는 코인의 총값을 나타내는 대신, 표에 있는 다양한 코인 유형의 카운트를 나타내는$$ ${\displaystyle {Xn}_{}}${\$displaystyle$X_{$n}$을 정의할 수 있었다.예를 들어 $X{\displaystyle {}_{}}$ ${\displaystyle {6\mathrm{}}_{}}$= ${\displaystyle 1}$,${\displaystyle 0,}$ 5 ${\displaystyle X_{6}=1,0,5}$을(를) 정의하여 6개의 1:1 추첨 후 테이블 위에 1/4, 0데임, 5 니켈이 있는 상태를 나타낼 수 있다$$.이 새로운 모델은 216개의 가능한 상태(즉, 6x6x6 상태, 각 3개의 동전 유형은 6무승부가 끝날 때까지 테이블 위에 0-5개의 동전을 가질 수 있기 때문에 6x6x6 상태)로 표현될 것이다.처음 추첨을 통해 상태 ${\displaystyle {X\mathrm{}}_{}}$ 1${\displaystyle {}_{}}$= ${\displaystyle 0,}$ ${\displaystyle 1}$,${\displaystyle 0}$ ${\displaystyle X_{1}=0,1,0}$이(가) 발생한다고 가정합시다$.$$현재$ ${\displaystyle {X\mathrm{}}_{}}$ 2$${\$displaystyle X_{1}}$를 달성할 $확률$은 ${\displaystyle {X\mathrm{}}_{}}$ 1$${\$displaystyle X_{$1}에 달려 있다$.$ 예를 들어 $상태{\displaystyle {}_{}}$ X${\displaystyle {}_{}{2\mathrm{}}_{}}$ =${\displaystyle 1}$, 0${\displaystyle ,}$ ${\displaystyle 1}${\$displaystyle X_{2}=1,0,1$}은$($는) 사용할 수 있다.두 번째 추첨 후, 세 번째 추첨은 지금까지 어떤 동전을 추첨했는가에 따라 결정되지만, 더 이상 첫 번째 주를 위해 추첨한 동전에만 국한되지 않는다(확률적으로 중요한 정보가 그 이후 시나리오에 추가되었기 때문이다).이러한 방식으로 $X{\displaystyle {}_{}}$ ${\displaystyle n_{}}$= ${\displaystyle i,}$ ${\displaystyle j,}$ k ${\displaystyle X_{n}=i,j,k$}=${\displaystyle i}$,j,k$}$ 상태의$$ 가능성은 X ${\displaystyle {\mathrm{n}}_{}}$- 1${\displaystyle {}_{}}$= ${\displaystyle \ell ,}$ ${\displaystyle m,}$ p ${\displaystyle X_{n-1}=\$el$,m,p}$ 상태의$$ 결과에 전적으로 의존한다.

형식 정의

이산 시간 마르코프 체인

이산 시간 마코프 체인은 마르코프 속성을 가진 일련의 랜덤 변수 X₁, X₂, X₃, ... 즉, 다음 상태로 이동할 확률은 현재 상태에만 의존하고 이전 상태는 그렇지 않다는 것이다.

${\displaystyle \Pr(X_{n+1}=x\mid X_{1}=x_{1},X_{2}=x_{2},\ldots ,X_{n}=x_{n})=\Pr(X_{n+1}=x\mid X_{n}=x_{n}),}$ if both conditional probabilities are well defined, that is, if ${\displaystyle \Pr(X_{1}=x_{1},\ldots, X_{n}=x_{n}}}>0.$$}$

X의_i 가능한 값은 체인의 상태 공간이라고 불리는 카운트 가능한 집합 S를 형성한다.

변형

• 시간균형 마르코프 체인은 다음과 같은 프로세스다.
  $${\displaystyle \Pr(X_{n+1}=x\mid X_{n}=y)=\Pr(X_{n}=x\mid X_{n-1}=y)}$$

  
  …의 전부로서전환 가능성은 n과 무관하다.
• 고정 마코프 체인은 다음과 같은 과정을 말한다.
  $${\displaystyle \Pr(X_{0}=x_{0},X_{1}=x_{1},\ldots,X_{k}=x_{0},X_{n+1}=x_{1},\ldots,X_{n+k}=x_{k}}}}}}},}}},},},}, {k}, {k}$$

  
  n과 k에 대해모든 고정 사슬은 베이지스의 통치에 의해 시간 동종이라는 것이 증명될 수 있다.
  시간균형 마르코프 체인이 정지하기 위해 필요하고 충분한 조건은 $X{\displaystyle {}_{}}$ ${\displaystyle {0\mathrm{}}_{}}$ ${\$ 스타일 $X_{0}}$의 분포가 마르코프 체인의 정지된 분포라는$$ 것이다.
• m이 유한한 경우 메모리를 가진 마르코프 체인(또는 순서 m의 마르코프 체인)은 만족스러운 과정이다.
  $${\displaystyle {\begin{aligned}{}&\Pr(X_{n}=x_{n}\mid X_{n-1}=x_{n-1},X_{n-2}=x_{n-2},\dots ,X_{1}=x_{1})\\=&\Pr(X_{n}=x_{n}\mid X_{n-1}=x_{n-1},X_{n-2}=x_{n-2},\dots ,X_{n-m}=x_{n-m}){\text{ for }}n>m\end{aligned}}}$$

  
  즉, 미래 상태는 과거 m 상태에 따라 달라진다.It is possible to construct a chain ${\displaystyle (Y_{n})}$ from ${\displaystyle (X_{n})}$ which has the 'classical' Markov property by taking as state space the ordered m-tuples of X values, i.e., ${\displaystyle Y_{n}=\left(X_{n},X_{n-1},\ldo$$ts ,X_{n-m+1}\오른쪽)}$.

연속시간 마르코프 체인

연속 시간 마코프 체인(X_t)_{t ≥ 0}은 유한 또는 계수 가능한 상태 공간 S, 상태 공간에 정의된 상태 공간 및 초기 확률 분포와 동일한 치수를 갖는 전환율 매트릭스 Q에 의해 정의된다.i ≠ j의 경우 원소 q는_ij 음이 아니며 상태 i에서 상태 j로 프로세스 전환 속도를 설명한다.요소 q는_ii (구체적인) 마르코프 체인의 확률 전이 행렬의 행 합이 0인 반면, 전환율 매트릭스의 각 행 합계는 0이 되도록 선택된다.

그 과정에는 세 가지 동등한 정의가 있다.^[49]

최소 정의

$X{\displaystyle {}_{}}$ ${\displaystyle t_{}}$ ${\$를 시간 t의 공정 상태를 설명하는 랜덤 변수로 하고$$, 공정이 시간 t의 상태 i에 있다고 가정한다.그러면 ${\displaystyle X}$ ${\displaystyle t_{}}$= i ${\displaystyle X_{t}=i$ ${\displaystyle X}$ t${\displaystyle {}_{}}$+ h${\displaystyle {}_{}}$= ${\displaystyle j_{}}$ ${\displaystyle X_{t+h}=j}$을(를) 아는 것은 이전 값: < ) ${\$, 모든 j에 대해 h → 0으로 독립적이다$$.

여기서$$ $\Delta {\displaystyle {}_{}}$ ${\displaystyle i_{}}$ ${\displaystyle j_{}}$ ${\$는 little-o 표기법을 사용하는 크로네커 델타다.$q{\displaystyle {}_{}}$ ${\displaystyle i_{}}$ ${\displaystyle j_{}}$ ${\$는 i에서 j로의 전환이 얼마나 빨리 일어나는지를 측정하는 것으로 볼 수 있다$$.

점프 체인/홀딩 시간 정의

프로세스의 n번째 점프를 설명하기 위한 이산형 시간 Markov 체인 Y를_n 정의하고, S가_i 속도 매개변수 -q로_YiYi 지수 분포를 따르는 각 주에서의 홀딩 시간을 설명하기 위해 변수₁ S, S₂, S, S를₃ 정의한다.

전환 확률 정의

n = 0, 1, 2, 3, ... 및 n: t₀, t₁, t, ...의 값까지₂ 인덱스된 모든 값에 대해, 이 시간에 기록된 모든 상태 i₀, i₂, i₁, i₃, i, ...는 이 값을 유지한다.

${\displaystyle \Pr(X_{t_{n+1}}=i_{n+1}\mid X_{t_{0}}=i_{0},X_{t_{1}}=i_{1},\ldots ,X_{t_{n}}=i_{n})=p_{i_{n}i_{n+1}}(t_{n+1}-t_{n})}$

여기서 p는_ij 전방 방정식의 해법이다(1차 미분 방정식)

${\displaystyle P'(t)=P(t)Q}$

초기 조건 P(0)는 ID 행렬이다.

유한 상태 공간

상태 공간이 유한한 경우, P의 (i, j)번째 요소가 다음과 같은 값을 갖는 전환 매트릭스라고 하는 행렬로 전환 확률 분포를 나타낼 수 있다.

${\displaystyle p_{ij}=\Pr(X_{n+1}=j\mid X_{n}=i).}$

P의 각 행은 1이고 모든 원소는 음이 아니기 때문에 P는 오른쪽 확률적 행렬이다.

고유 벡터 및 단순화에 대한 고정 분포 관계

고정 분포 π은 (행) 벡터로서, 입력은 음이 아니고 합이 1인 경우, 그 위에 있는 전환 행렬 P의 작동에 의해 변경되지 않으며, 따라서 다음과 같이 정의된다.

${\displaystyle \pi \mathbf {P} =\pi.}$

이 정의를 고유 벡터의 정의와 비교함으로써 우리는 두 개념들이 연관되어 있고, 또 그 두 개념들이 연관되어 있음을 알 수 있다.

${\displaystyle \pi ={\frac {e}{\sum _{e_{i}}}}$

고유값이 1인 변환 매트릭스 P의 왼쪽 고유 벡터 e의 배수인 정규화$\underset{}{}$ $\underset{}{i}$ $\underset{}{}{}_{}$ $\mathrm{i}{}_{}$= 1 ${\textstyle \sum _{i}\pi _{i}=1$이다.장치 고유 벡터가 둘 이상일 경우 해당 정지 상태의 가중 합도 정지 상태가 된다.그러나 마르코프 체인의 경우 일반적으로 일부 초기 분포에 대한 분포 순서의 한계인 정지 상태에 더 관심이 있다.

고정 분포 값 $\pi {\displaystyle {}_{}}$ ${\displaystyle i_{}}$ ${\$는 P의 상태 공간과 연관되며, 고유$$ 벡터의 상대적 비율은 보존된다.π의 성분은 양성이며 그 합이 통일이라는 제약조건은 $\sum \underset{}{}$ $i_{}$ ${}_{}$ $\cdot {}_{}$i = $1$ ${\textstyle \sum _{i}1\cdot \pi \{i}=1}$로 다시 쓸 수 있기 때문에 we의$$ 점 산물은 모두 1이 통일이고 is은 심플렉스 위에 놓여 있음을 알 수 있다.

유한 상태 공간의 시간균형 마르코프 체인

이 절에는 참조, 관련 판독 또는 외부 링크 목록이 포함되지만, 인라인 인용구가 부족하기 때문에 출처가 불분명하다. 보다 정확한 인용구를 도입하여 이 섹션을 개선할 수 있도록 도와주십시오. (2012년 2월) (이 템플릿 메시지를 제거하는 방법과 시기 알아보기)

마르코프 체인이 시간 동종인 경우, 전환 매트릭스 P는 각 단계 후에 동일하므로, k-step 전환 확률은 전환 매트릭스^k P의 k번째 전력으로 계산할 수 있다.

마코프 체인이 회복불능이고 주기적인 경우, 독특한 고정 분포 π이 있다.^[50]또한 이 경우 P는^k 각 행이 고정된 분포인 순위 1 행렬로 수렴된다. π:

${\displaystyle \lim_{k\to \inflt }\mathbf {P}^{k}=\mathbf {1} \pi }$

여기서 1은 모든 항목이 1인 열 벡터다.이것은 페론-프로베니우스 정리에 의해 명시된다.어떤 방법으로든 림 $\underset{}{k}$→ $\underset{}{\mathrm{\infty }}$ ${}^{}$ $\underset{}{}{\mathbf{}}^{}$ ${\$}\$mathbf {P}$^{$k}}}}$이 발견되면$$, 아래에서 설명하듯이 어떤 시작 분포에 대해서도 해당 마르코프 체인의 고정 분포를 쉽게 결정할 수 있다.

일부 확률론적 매트릭스 $\underset{}{P}$의 경우 다음과 같이 고정 분포가 존재하는 동안에는 $\underset{}{한계}$ 림 k$\underset{}{}$→ $\underset{}{\mathrm{\infty }}$ $\underset{}{}{\mathbf{}}^{}$ ${}^{}$ ${\$가 존재하지 않는다$$.

${\displaystyle \mathbf {P} ={\begin{pmatrix}0&#1&#0\end{pmatrix}}\qquad \mathbf {P}^{2k}=I\qquad \mathbf {P} ^{2k+1}=\mathbf {P}}}$

${\displaystyle {\begin{pmatrix}{\frac {1}{2}}&{\frac {1}{2}}\end{pmatrix}}{\begin{pmatrix}0&1\\1&0\end{pmatrix}}={\begin{pmatrix}{\frac {1}{2}}&{\frac {1}{2}}\end{pmatrix}}}$

(이 예는 주기적인 마르코프 체인을 예시한다.)

고려해야 할 여러 가지 특수한 경우가 있기 때문에, 이 한도가 존재한다면 찾아내는 과정이 긴 과제가 될 수 있다.하지만, 이 한계를 찾는 데 도움이 될 수 있는 많은 기술들이 있다.P를 n×n 행렬로 하고 $Q\mathbf{}$= $\underset{}{lim}$ k$\underset{}{}$→ $\underset{}{\mathrm{\infty }}$ ${}^{}$ $\underset{}{}{\mathbf{}}^{}$. ${\textstyle \mathbf {Q} =\lim _{k\to \inft }\mathbf {P} ^{k}}$를 정의한다.$}$

는 것은 언제나 사실이다.

${\displaystyle \mathbf {QP} =\mathbf {Q} .}$

양쪽에서 Q를 빼서 인수 후 수율 계산

${\displaystyle \mathbf {Q}(\mathbf {P} -\mathbf {I} _{n}=\mathbf {0} _{n,n})$

여기서 나는_n n 크기의 아이덴티티 매트릭스, 0은_n,n n×n 크기의 제로 매트릭스다.확률 매트릭스를 함께 곱하면 항상 또 다른 확률 매트릭스가 생성되므로 Q는 확률 매트릭스여야 한다(위의 정의 참조).위 행렬 방정식과 Q가 Q에 대해 해결하기 위한 확률적 행렬이라는 사실을 사용하는 것이 때로는 충분하다.P의 각 행의 합이 1이라는 사실을 포함하면 n+1의 미지수를 결정하는 방정식이 있기 때문에, 한편으로 Q의 한 행을 선택하고 그 원소를 각각 한 행씩 대체하면, 다른 한편으로 벡터 0의 해당 원소(동일한 열에 있는 한 행)를 대체하고, 다음 le를 대체하면 계산적으로 더 쉽다.ft-이 후자의 벡터를 Q를 찾기 위해 변환된 전 행렬의 역행렬로 곱한다.

이를 위한 한 가지 방법이 있다. 첫째, 매트릭스 A를 가장 오른쪽 열로 1의 모든 열로 교체하여 반환하는 함수 f(A)를 정의한다.[f(P_n - I)]⁻¹가 있으면^[51][50]

${\displaystyle \mathbf {Q} =f(\mathbf {0} _{n})[f(\mathbf {P} -\mathbf {I} _{n}]^{-1}.}$

설명:원래의 행렬 방정식은 n×n 변수에 있는 n×n 선형 방정식의 체계와 동등하다.그리고 Q가 각 행의 합계가 1인 우 확률적 행렬이라는 사실로부터 더 많은 선형 방정식이 있다.그래서 그것은 n×n 변수에 대해 해결하기 위해 (n×n+n) 방정식의 어떤 n×n 독립적 선형 방정식이 필요하다.이 예에서 "Q에 (P-In)의 맨 오른쪽 열을 곱한 값"의 n 방정식은 확률적인 값으로 대체되었다.

한 가지 주목해야 할 것은 P의 주 대각선 상에 1과 같은 요소_i,i P가 있고 ih 행이나 열이 그렇지 않으면 0으로 채워진다면, 그 행이나 열은 이후의 모든 힘 P에서^k 변하지 않게 된다는 것이다.따라서 Ith 행 또는 Q의 열은 1과 0이 P와 같은 위치에 있게 된다.

고정된 분배에 대한 수렴 속도

이 절에는 참조, 관련 판독 또는 외부 링크 목록이 포함되지만, 인라인 인용구가 부족하기 때문에 출처가 불분명하다. 보다 정확한 인용구를 도입하여 이 섹션을 개선할 수 있도록 도와주십시오. (2012년 2월) (이 템플릿 메시지를 제거하는 방법과 시기 알아보기)

앞에서 설명한 것처럼 방정식 $\pi {\displaystyle \mathit{}}$= ${\displaystyle \pi \mathbf{}}$ P${\displaystyle }$, ${\displaystyle {\boldsymbol {\pi }}={\boldsymbol {\pi }}}}}},$ $$(존재할 경우) 정지(또는 안정 상태) 분포 π은 행 확률행렬 P의 왼쪽 고유 벡터다.그런 다음 P가 대각선적으로 또는 동등하게 P가 n개의 선형 독립 고유 벡터를 가지고 있다고 가정하면, 수렴 속도는 다음과 같이 상세하게 설명된다.(비대각선화, 즉 결함이 있는 행렬의 경우, 요르단 정상 형태의 P로 시작하여 유사한 방식으로 약간 더 관련된 주장을 진행할 수 있다.^[52]

U를 고유 벡터의 행렬로 하고(각각 L2 규범이 1과 동일한 것으로 정규화) 각 열이 P의 왼쪽 고유 벡터, 즉 matrix = diag((, diag, λ₁₂, λ₃, λ_n, ...)의 왼쪽 고유값의 대각 행렬로 한다.그리고 나서 에겐데 콤포메이션으로

${\displaystyle \mathbf {P} =\mathbf {U\Sigma U} ^{-1}.}$

다음과 같이 고유값을 열거하도록 한다.

${\displaystyle 1= \data _{1} > \bodda \{2} \geq \cdots \geq \geq \geda _{n} .}$

P는 행 확률적 행렬이므로 가장 큰 왼쪽 고유값은 1이다.고유한 고정 분포가 있는 경우 가장 큰 고유값과 해당 고유 벡터도 고유하다(위의 고정 분포 방정식을 해결하는 다른 π이 없기 때문이다).U_i 행렬의 i번째 열, 즉 u는_i λ에_i 해당하는 P의 왼쪽 고유 벡터다.또한 x는 유효한 확률 분포를 나타내는 길이 n 행 벡터가 되도록 한다. 고유 벡터 u_i ${\displaystyle {}^{}}$ $R{\displaystyle {\mathbb{}}^{}}$ ${\displaystyle \mathb {R} ^{n}},$ 우리는$$ 쓸 수 있다.

${\displaystyle \mathbf {x} ^{\mathsf {T}=\sum _{n}a_{i}}\mathb {u} _{i}\qquad a_{i}\in \mathb {R}}}$

x에 오른쪽에서 P를 곱하고 이 수술을 계속하면 결국 정지 분포 distribution을 얻게 된다.즉, = = u_i ← xPP...P = xP^k as k → ∞.그 말은

${\displaystyle {\begin{aligned}{\boldsymbol {\pi }}^{(k)}&=\mathbf {x} \left(\mathbf {U\Sigma U} ^{-1}\right)\left(\mathbf {U\Sigma U} ^{-1}\right)\cdots \left(\mathbf {U\Sigma U} ^{-1}\right)\\&, =\mathbf{xU\Sigma}^{k}\mathbf{U}^{)}\\&, =\left(a_{1}\mathbf{너}_{1}^{\mathsf{T}}+a_{2}\mathbf{너}_{2}^{\mathsf{T}}+\cdots{n}\mathbf{너}_{n}^{\mathsf{T}}+a_ \right)\mathbf{U\Sigma}^{k}\mathbf{U}^{)}\\&, =a_{1}\lambda _{1}^{k}\mathbf{u}_{1}^{\mathsf{T}}}+a_{n}+\cdots _{2}^{k}\mathbf{u}_{2}^{\mathsf{T}+a_{2}\lambda.\lambda _{n}^{k}\mathbf {u} _{n}^{\mathsf {T}}&&u_{i}\bot u_{j}{\text{ for }}i\neq j\\&=\lambda _{1}^{k}\left\{a_{1}\mathbf {u} _{1}^{\mathsf {T}}+a_{2}}\왼쪽 \frac _{2}}:{\messda _{1}}\오른쪽)^{k}\mathbf {u} _{2}^{\mathsf {T}+a_{3}}\왼쪽 \frac _{3}{{3}}{1}}\오른쪽)^{k}\mathbf {u} _{3}^{{3}^{\mathsf{T}+\cdots +a_{n}\왼쪽({\frac {\lambda _{n}}{\lambda _{1}}\오른쪽)^{k}\mathbf {u} _{n}^{{n}^{\mathsf{T}\right\}\end{aigned}}}}}$

π = u이므로₁ π은^(k) λ₂/λ의₁ 순서로 exponentially에 k → speed으로 접근한다.이것은 ${\displaystyle \lambda {}_{}}$ ${\displaystyle {2\mathrm{}}_{}{}_{}}$⋯ n${\displaystyle }$≥${\displaystyle {}_{}{n}_{}}$ n , ${\displaystyle \lambda _{2} \geq \cdots \geq \lambda _{n}}},$ 따라서$$ λ₂/λ이₁ 지배적인 용어이기 때문이다.비율이 작을수록 수렴 속도가 빠르다.^[53]상태 분포의 무작위 노이즈 π도 정지 분포로의 수렴 속도를 높일 수 있다.^[54]

일반 상태 공간

해리스 체인

주 공간이 유한한 마르코프 체인에 대한 많은 결과는 해리스 체인을 통해 헤아릴 수 없는 주 공간을 가진 체인으로 일반화될 수 있다.

마르코프 체인 몬테 카를로 방법에서 마르코프 체인의 사용은 프로세스가 연속적인 상태 공간을 따르는 경우를 다룬다.

로컬로 상호 작용하는 마르코프 체인

진화가 다른 마르코프 체인의 상태를 고려하는 마르코프 체인의 컬렉션을 고려한다면, 마르코프 체인은 현지에서 상호 작용하는 개념과 관련이 있다.이는 주 공간에 (카르테시안-) 제품 형태가 있는 상황에 해당한다.상호작용하는 입자 시스템과 확률적 세포 자동자(확률적 세포 자동자)를 참조하십시오.Markov 프로세스의^[55] 상호 작용에 대한 예제를 참조하십시오^[56].

특성.

두 상태는 양쪽 모두 긍정적인 확률을 가진 일련의 전환에 의해 서로 도달할 수 있는 경우 서로 의사소통한다.이것은 통신 클래스의 집합을 산출하는 동등성 관계다.수업에서 빠질 확률이 0이면 휴강한다.마르코프 체인은 의사소통하는 하나의 계급, 즉 주의 공간이 있다면 되돌릴 수 없다.

$k{\displaystyle }$ ${\displaystyle k}$이(가) i에서 시작하여 도달할 수 있는 전환 수에 대한 가장 큰 공통점인 경우$$ 상태 i는 마침표 $k{\displaystyle }$ ${\displaystyle$ k$}$을(를) 가진다.즉,

${\displaystyle k=\gcd\{n]0:\Pr(X_{n}=i\mid X_{0}=i)>0\}}}$

상태 i는 i에서 시작하여 체인이 결코 i로 되돌아오지 않을 가능성이 0이 아닌 경우 일시적이라고 한다.그렇지 않으면 재발한다.반복 상태 i의 경우 평균 타격 시간은 다음과 같이 정의된다.

${\displaystyle M_{i}=E[]T_{i}]=\sum _{n=1}^{\n\cdot f_{i}^{(n)}}}$

State $i$는 ${\displaystyle {Mi}_{}}$ ${\$가 유한한 경우 양의 반복이고, 그렇지 않은 경우 null이 반복된다.주기성, 과도성, 재발 및 양수 및 무효 재발은 클래스 속성이다. 즉, 한 국가가 속성을 가지고 있다면 통신 클래스의 모든 주가 속성을 가지고 있다.

상태 i는 상태로부터 나가는 전환이 없을 경우 흡수라고 불린다.

에고다이시티

만약 그것이 주기적이고 긍정적인 재발이라면, 1세는 에르고딕적이라고 한다.즉, 상태 i가 재발하면 에르고딕적이며, 기간이 1이며, 평균 재발 시간이 유한하다.만약 돌이킬 수 없는 마르코프 체인의 모든 상태가 에고딕이라면, 그 체인은 에고딕이라고 한다.^{[dubious – discuss]}

유한상태의 불가침 마르코프 체인은 주기적인 상태를 가지고 있다면 에고다이컬임을 알 수 있다.보다 일반적으로 마르코프 체인은 숫자 N보다 작거나 같은 수의 스텝에서 다른 상태로부터 어떤 상태에 도달할 수 있는 숫자 N이 있는 경우 에르고딕적이다.완전히 연결된 전환 매트릭스의 경우, 모든 전환이 0이 아닌 확률을 갖는 경우, 이 조건은 N = 1로 충족된다.

둘 이상의 주와 한 주 당 하나의 진행 중인 전환만이 있는 마르코프 체인은 되돌릴 수 없거나 주기적이지 않기 때문에 에고딕적일 수 없다.

마르코비아의 표현

어떤 경우에는 겉으로 보기에 마코비아가 아닌 과정들이 '현재'와 '미래' 상태의 개념을 확장하여 구성한 마코비안적 표현을 여전히 가지고 있을 수도 있다.예를 들어 X를 마르코비안이 아닌 프로세스로 하자.그런 다음 각 Y 상태가 X 상태의 시간 간격을 나타내도록 프로세스 Y를 정의하십시오.수학적으로 이것은 다음과 같은 형태를 취한다.

$[\displaystyle Y(t)={\big \{}Xs):s\in[a(t),b(t)]\,{\big \}}.}$

Y가 마코프 속성을 가지고 있다면 X의 마코브 표현이다.

마르코비안 표현을 사용하는 비 마코비안 공정의 예로는 1보다 큰 순서의 자기 회귀 시간 시리즈가 있다.^[57]

히트 타임즈

타격 시간은 체인이 주어진 상태 또는 일련의 상태에 도착할 때까지 주어진 상태 집합에서 시작하는 시간이다.그러한 기간의 분포는 위상 유형 분포를 가진다.그러한 가장 간단한 분포는 단일 지수 분포 전환의 분포다.

예상 적중 시간

상태 A ⊆ S의 하위 집합에 대해, 타격 시간의 벡터^A k(${\displaystyle {여기}_{}^{}}$서 요소 k ${\displaystyle {}_{}^{}}${\$displaystyle k_{i$}^{A$})$는 체인이 세트 A의 상태 중 하나로 들어가는 상태 i에서 시작하는 기대값을 나타냄$$)에^[58] 대한 최소 비음극 솔루션이다.

${\displaystyle {\displaysty}k_{i}^{A}=0&{\text{{}}{{}i\in A\\-\sum _{j\q_{ij}k_{j}^{}}A}=1&{\text{{}}}}}}}}i\notin A의 경우\end{정렬}}}$

시간역전

CTMC X의_t 경우 시간역전 프로세스는 $X{\displaystyle {\stackrel{}{}}_{}}$ ${\displaystyle {\stackrel{}{^}}_{}}$ t${\displaystyle {}_{}}$= ${\displaystyle X_{}}$ ${\displaystyle {}_{}}$- ${\displaystyle t_{}}$ ${\$로 정의된다$.$ 켈리의 보조정리에서는 이 과정이 전진과정과 동일한 정지분포를 갖는다.

체인은 역전 과정이 전진 과정과 동일하면 되돌릴 수 있다고 한다.Kolmogorov의 기준은 공정이 되돌릴 수 있는 필요조건과 충분한 조건은 폐쇄 루프 주위의 전환율 산물이 양방향에서 동일해야 한다는 것이다.

임베디드 마르코프 체인

에고다이컬 연속시간 마코프 체인 Q의 고정 확률 분포인 π을 찾는 한 가지 방법은 우선 내장된 마코프 체인(EMC)을 찾는 것이다.엄밀히 말하면 EMC는 정기적인 이산 시간 마코프 체인으로, 때로는 점프 프로세스라고도 한다.EMC, S의 1단계 전환 확률 매트릭스의 각 요소는_ij s로 표시되며 상태 i에서 상태 j로 전환하는 조건부 확률을 나타낸다.이 조건부 확률은 다음을 통해 찾을 수 있다.

${\displaystyle s_{ij}={\frac {q_{ij}}{\sum_{k\neq i}}{ik}}&{\text{}i\neq j\\\0&{\text}}}.\end{case}}}$

이로부터 S는 다음과 같이 쓰일 수 있다.

${\displaystyle S=I-\left(\operatorname {diag}(Q)\오른쪽)^{-1}Q}$

여기서 I는 아이덴티티 매트릭스이고 diag(Q)는 매트릭스 Q에서 주 대각선을 선택하고 다른 모든 원소를 0으로 설정하여 형성된 대각 행렬이다.

고정 확률 분포 벡터를 찾으려면 다음에 다음과 같은 $such$$${\$displaystyle \varphi }$을(를) 찾아야 한다.

${\displaystyle \varphi S=\varphi ,}$

$\phi {\displaystyle }$ ${\$$displaystyle \varphi$ $}$의 모든 요소가$$ 0보다 크고 ${\$= 1. 여기서 π은 다음과 같이 찾을 수 있다.

${\displaystyle \pi ={-\varphi(\operatorname {diag}(Q))^{-1}{1} \좌측\\\varphi(\operatorname {diag}(Q)^{1}}}}$

(S는 Q가 아니더라도 주기적일 수 있다.π이 발견되면 단위 벡터로 정규화해야 한다.)

연속 시간 Markov 체인에 의해 도출될 수 있는 또 다른 이산 시간 프로세스는 Δ-skeleton, 즉 Δ 단위 간격으로 X(t)를 관찰하여 형성된 (분리 시간) 마코프 체인이 있다.랜덤 변수 X(0), X(Δ), X(2Δ), ...는 Δ-skeleton이 방문한 상태의 순서를 제공한다.

마르코프 체인의 특수 유형

마르코프 모델

마르코프 모델은 변화하는 시스템을 모델링하는 데 사용된다.모든 순차적 상태를 관찰할 수 있는지 여부와 관찰한 결과에 따라 시스템을 조정해야 하는지에 따라 마르코프 체인을 일반화하는 4가지 주요 모델이 있다.

	시스템 상태를 완전히 관찰할 수 있음	시스템 상태를 부분적으로 관측할 수 있음
시스템은 자율적이다.	마르코프 체인	히든 마르코프 모델
시스템이 제어됨	마르코프 의사결정 과정	부분적으로 관측 가능한 마르코프 의사결정 과정

베르누이 계획

베르누이 체인은 전환 확률 매트릭스가 동일한 행을 갖는 마르코프 체인의 특수한 경우로서, 다음 상태는 (과거 상태와 독립된 것에 더하여) 현재 상태에서도 독립적이라는 것을 의미한다.두 주만 가능한 베르누이 계획은 베르누이 과정으로 알려져 있다.

그러나, 오렌슈타인 이소모르피즘 정리에 의해, 모든 Aperiodic과 unreducable Markov 체인은 베르누이 계획과 이소모르프라는 것에 주목한다.^[59] 따라서, 사람들은 똑같이 마르코프 체인이 베르누이 계획의 "특수 사례"라고 주장할 수 있다.이형질성은 일반적으로 복잡한 암기법을 필요로 한다.이소모르피즘의 정리는 심지어 조금 더 강하다: 그것은 어떤 고정된 확률적 과정이 베르누이 계획과 이소모르프라고 말한다; 마르코프 체인은 그러한 예들 중 하나일 뿐이다.

유한형 하위교대

마르코프 행렬이 유한 그래프의 인접 행렬로 대체될 때, 그 결과의 변화는 위상학적 마르코프 체인 또는 유한 유형의 하위 교대라고 불린다.^[59]인접 행렬과 호환되는 마르코프 행렬은 하위 교대조에 대한 측정을 제공할 수 있다.많은 혼란스러운 동적 시스템은 위상학적 마르코프 체인에 이형성적이다. 예를 들어 폐쇄된 다지관의 차이점들을 포함한다. 프루엣-Thue-Morse 시스템, Chacon 시스템, sofic 시스템, 맥락 없는 시스템 및 블록 코딩 시스템.^[59]

적용들

연구는 물리, 화학, 생물학, 의학, 음악, 게임 이론, 스포츠와 같은 광범위한 주제에 마르코프 체인의 응용과 유용성을 보고했다.

물리학

마르코비아 시스템은 시스템의 알려지지 않았거나 모델링되지 않은 세부사항을 나타내기 위해 확률을 사용할 때마다 열역학 및 통계역학에서 광범위하게 나타난다. 역학이 시간에 따라 다르다고 가정할 수 있고, 주 설명에 이미 포함되지 않은 관련 이력을 고려할 필요가 없는 경우.^[60][61]예를 들어 열역학 상태는 획득하기 어렵거나 비용이 많이 드는 확률 분포에서 작동한다.따라서 마르코프 체인 몬테 카를로 방법은 블랙박스에서 무작위로 표본을 추출하여 다양한 물체에 걸쳐 속성의 확률분포를 대략적으로 파악할 수 있다.^[61]

양자역학의 경로 적분형식에 있는 그 길은 마르코프 체인이다.^[62]

마코프 체인은 격자 QCD 시뮬레이션에 사용된다.^[63]

화학

반응 네트워크는 여러 반응과 화학 종을 포함하는 화학 시스템이다.그러한 네트워크의 가장 단순한 확률적 모델은 체인의 가능한 전환으로 모델링된 반응과 각 종의 분자 수가 주를 이루는 연속 시간 마코프 체인으로 시스템을 취급한다.^[64]마르코프 체인과 연속 시간 마르코프 과정은 물리 시스템이 마르코프 속성과 근접하게 근접한 화학에서 유용하다.예를 들어, 상태 A에 있는 용액의 많은 n개의 분자를 상상해 보십시오. 각 분자는 특정 평균 속도로 상태 B에 화학 반응을 일으킬 수 있다.아마도 분자는 효소일 것이고, 상태는 그것이 어떻게 접히는가를 가리킨다.어떤 단일 효소의 상태는 마르코프 사슬을 따르며, 분자는 본질적으로 서로 독립적이기 때문에, 한 번에 상태 A 또는 B에 있는 분자의 수는 주어진 분자가 그 상태에 있을 확률을 n배로 한다.

고전적인 효소 활성 모델인 Michaelis-Menten 키네틱스는 마르코프 사슬로 볼 수 있으며, 매 단계마다 어떤 방향으로 반응이 진행된다.Michaelis-Menten은 상당히 간단하지만, 훨씬 더 복잡한 반응 네트워크도 마르코프 체인으로 모델링할 수 있다.^[65]

또한 마르코프 체인에 기초한 알고리즘을 사용하여 약품이나 천연물과 같은 원하는 종류의 화합물을 향해 실리코 내 화학 물질의 단편 기반 성장을 집중시켰다.^[66]분자가 자라면서, 초기 분자로부터 파편을 "전류" 상태로 선택한다.그것은 자신의 과거를 알지 못한다(즉, 그것에 이미 결부되어 있는 것을 알지 못한다).그런 다음 파편이 부착되면 다음 상태로 전환된다.전이 확률은 실제 화합물 등급의 데이터베이스에 대해 훈련된다.^[67]

또한 복합체의 성장(및 구성)은 마르코프 체인을 사용하여 모델링할 수 있다.성장하는 폴리머 체인을 구성하는 모노머의 반응도비에 기초하여 체인의 구성을 계산할 수 있다(예를 들어, 모노머가 교대로 추가하는 경향이 있는지 또는 동일한 모노머의 장시간에 추가하는 경향이 있는지 여부).강직 효과로 인해 2차 마코프 효과는 일부 폴리머 체인의 성장에도 영향을 미칠 수 있다.

이와 유사하게, 일부 상피성 초산염 물질의 결정화와 성장을 마르코프 체인에 의해 정확하게 설명할 수 있다고 제안되었다.^[68]

생물학

마르코프 체인은 생물학의 다양한 분야에서 사용된다.주목할 만한 예는 다음과 같다.

• DNA 진화의 대부분의 모델들이 연속 시간 마코프 체인을 사용하여 게놈의 특정 부지에 존재하는 뉴클레오티드를 묘사하는 Phylgenetics and bio informatics.
• 특히 마르코프 체인이 행렬 모집단 모델의 이론적 연구에서 중심 도구인 인구 역학.
• 예를 들어, 마코프 체인이 포유류 신피질을 시뮬레이션하는 데 사용된 신경생물학.^[69]
• 시스템 생물학, 예를 들어 단일 세포의 바이러스 감염 모델링.^[70]
• 질병 발생 및 전염병 모델링을 위한 구획 모델.

테스트

여러 이론가들은 마코프 체인을 결합하여 "마코프 담요"를 형성하고, 이들 체인을 여러 재귀적 층으로 배열("웨이퍼링")하며, 보다 효율적인 시험 세트(샘플)를 생산하는 방법인 마코프 체인 통계 시험(MCST)의 아이디어를 전체 시험의 대체물로 제안했다.MCST는 임시 상태 기반 네트워크에서도 사용된다; 칠루쿠리 외 연구진 논문의 "객체 감지 및 추적에 응용하는 증거 융합을 위한 임시 불확실성 추론 네트워크"(ScienceDirect)는 MCST를 더 광범위한 응용 분야에 적용하기 위한 배경과 사례 연구를 제공한다.

일조 강도 변동성

일조 강도 변동성 평가는 태양광 발전 용도에 유용하다.시간의 경과에 따른 모든 위치에서 일조 강도 변동은 주로 하늘 돔을 가로지르는 태양 경로의 결정론적 변동성과 구름의 변동성의 결과물이다.지구 표면에서 접근 가능한 일조 강도의 변동성은 마코프 체인을 사용하여 모델링되었으며,^{[71][72][73][74]} 여기에는 투명하고 흐릿한 두 상태를 마코프 체인으로 모델링하는 것도 포함된다.^[75][76]

음성인식

히든 마코프 모델은 대부분의 현대 자동 음성 인식 시스템의 기본이다.

정보이론

마르코프 체인은 정보 처리 전반에 걸쳐 사용된다.정보이론의 장을 한 번에 만들어낸 클로드 섀넌의 유명한 1948년 논문 A수학적 의사소통 이론은 영어의 마르코프 모델링을 통해 엔트로피 개념을 도입함으로써 문을 연다.그러한 이상화된 모델은 많은 시스템의 통계적 규칙성을 포착할 수 있다.시스템의 전체 구조를 완벽하게 설명하지 않더라도, 그러한 신호 모델은 산술 코딩과 같은 엔트로피 인코딩 기법을 통해 매우 효과적인 데이터 압축을 가능하게 할 수 있다.그들은 또한 효과적인 상태 추정과 패턴 인식을 허용한다.마르코프 체인도 학습 강화에 중요한 역할을 한다.

마르코프 체인은 전화 네트워크(오류 교정을 위해 비테비 알고리즘을 사용), 음성 인식 및 생물정보학(재조정 검출 등^[77]) 등 다양한 분야에서 중요한 도구인 숨겨진 마르코프 모델의 기반이기도 하다.

LZMA 무손실 데이터 압축 알고리즘은 마코프 체인과 Lempel-Ziv 압축을 결합하여 매우 높은 압축 비율을 달성한다.

큐잉 이론

마르코프 체인은 큐(Queuering 이론)의 분석적 처리의 기초가 된다.애그너 크라우프 에를랑은 1917년에 이 주제를 시작했다.^[78]이것은 메시지들이 종종 제한된 자원(대역폭 등)을 위해 경쟁해야 하는 통신 네트워크의 성능을 최적화하는 데 중요한 역할을 한다.^[79]

수많은 대기열 모델들이 연속 시간 마코프 체인을 사용한다.예를 들어, M/M/1 큐는 연합 수송 이동 본부는non-negative의 정수에 나는에서 나는 굴복하게 상승 전환+1비율로 λ 포아송 과정에 따라 직업 사람을 묘사하고 일어난다 나는에서 나는 동시에 전환 1(에 대한 거야. 1입니다.)률μ(직업 서비스번 기하 급수적으로 분포한다)에 완성된 서비스를 설명하게 발생하는 –(출발)에서queu.

인터넷 응용 프로그램

구글이 사용하는 웹 페이지의 페이지랭크는 마르코프 체인에 의해 정의된다.^[80][81][82]모든 (알려진) 웹 페이지의 다음 마코프 체인에 있는 고정 배포에서$$ $i{\displaystyle }$ ${\displaystyle$ i$}$페이지에 있을 확률이다.If ${\displaystyle N}$ is the number of known webpages, and a page ${\displaystyle i}$ has ${\displaystyle k_{i}}$ links to it then it has transition probability ${\displaystyle {\frac {\alpha }{k_{i}}}+{\frac {1-\alpha }{N}}}$ for all pages that are linked to and ${\displaystyle \frac{1-\alpha }{N}}$$$연결되지 않은 모든 페이지에 대해$$ ${\displaystyle {\frac {1-\alpha }{N}}.$매개 변수 $\alpha {\displaystyle }$ ${\displaystyle \alpha }$은(^[83]는) 0.15 정도로 간주된다$$.

마코프 모델은 사용자의 웹 네비게이션 동작을 분석하는 데도 이용되었다.특정 웹사이트의 사용자 웹 링크 전환은 1차 또는 2차 마코프 모델을 사용하여 모델링할 수 있으며, 향후 탐색에 관한 예측과 개별 사용자의 웹 페이지 개인화에 사용할 수 있다.

통계

마르코프 체인 방법은 또한 마르코프 체인 몬테 카를로(MMC)라고 불리는 과정을 통해 매우 복잡한 원하는 확률 분포를 정확하게 반영하기 위해 무작위 숫자의 시퀀스를 생성하는 데 매우 중요해졌다.최근 몇 년 동안 이것은 베이지안 추론 방법의 실행 가능성에 혁명을 일으켜 광범위한 후방 분포를 시뮬레이션하고 그 매개변수를 숫자로 찾을 수 있게 했다.

경제금융

마르코프 체인은 금융과 경제학에서 소득 분배, 기업의 규모 분배, 자산 가격, 시장 붕괴를 포함한 다양한 다른 현상을 모델링하기 위해 사용된다.D. G. Champernowne는 1953년에 소득분배의 마르코프 체인 모델을 구축했다.^[84]허버트 A. 사이먼과 공동저자인 찰스 보니니는 마르코프 체인 모델을 사용하여 고정된 크기의 율(Yule) 분포를 도출했다.^[85]루이 바첼리에르는 주가가 무작정 걷기를 따른다는 것을 가장 먼저 관찰했다.^[86]무작위 보행은 나중에 효율적 시장 가설을 지지하는 증거로 보여졌고 무작위 보행 모델이 1960년대 문헌에서 인기를 끌었다.^[87]제임스 D는 경제 주기의 체제 전환 모델을 대중화했다. Markov 체인을 사용하여 높은 GDP 성장 기간과 낮은 GDP 성장 기간 사이의 전환(또는 그 대안으로 경제 팽창과 경기 침체)을 모델링한 Hamilton(1989)이다.^[88]보다 최근의 예는 로랑 E. 칼벳과 애들라이 J의 다중추적 모델 전환이다.피셔, 이전의 정권 교체 모델들의 편리함을 기반으로 한다.^[89][90]임의로 큰 마코프 체인을 사용해 자산 수익의 변동성 수준을 견인한다.

역동적인 거시경제학은 마르코프 체인을 많이 이용한다.예를 들어, 마코프 체인을 사용하여 일반 평형 환경에서 자본(주식)의 가격을 자연적으로 모델링하는 것이 그 예다.^[91]

신용평가사들은 신용등급이 다른 채권에 대해 매년 전환확률표를 작성한다.^[92]

사회과학

마르코프 체인은 일반적으로 현재 구조 구성이 미래의 결과를 조건으로 하는 경로 의존적 인수를 기술하는 데 사용된다.그 예가 이 사상의 개혁인데, 원래 카를 마르크스의 다스 카피탈에 기인하여 경제 발전을 자본주의의 발흥과 결부시킨 것이다.현재의 연구에서는, 한 국가가 특정한 경제 발전 수준에 도달하는 방법을 모델링하기 위해 마르코프 체인을 사용하는 것이 일반적이며, 중산층의 규모, 도시와 농촌의 거주 비율, 정치 동원의 비율 등과 같은 구조적 요인의 구성이, 보다 높은 전환의 가능성을 발생시킬 것이다.민주 정권에 대한 ^[93]비호감적

게임.

마르코프 체인은 많은 운명의 게임을 모델링하는데 사용될 수 있다.^[1]예를 들어 어린이 게임 뱀과 사다리와 "하이 호! 체리 오"는 마르코프 체인으로 정확히 표현된다.각 턴마다 플레이어는 주어진 상태(주어진 사각형)에서 출발하며, 거기서부터 특정 다른 상태로 이동할 확률은 고정되어 있다(스쿼어).

음악

마르코프 체인은 알고리즘 음악 작곡에, 특히 Csound, Max, SuperCollider와 같은 소프트웨어에 고용되어 있다.1차 체인에서는 시스템의 상태가 노트 또는 피치 값이 되고, 각 노트에 대한 확률 벡터가 구성되어 전환 확률 매트릭스(아래 참조)를 완성한다.알고리즘은 MIDI 노트 값, 주파수(Hz) 또는 기타 바람직한 메트릭일 수 있는 전환 매트릭스 가중치를 기반으로 출력 노트 값을 생성하도록 구성된다.^[94]

1차 행렬

참고	A	C♯	E♭
A	0.1	0.6	0.3
C♯	0.25	0.05	0.7
E♭	0.7	0.3	0

2차 행렬

메모들	A	D	G
AA	0.18	0.6	0.22
AD	0.5	0.5	0
AG	0.15	0.75	0.1
DD	0	0	1
DA	0.25	0	0.75
DG	0.9	0.1	0
GG	0.4	0.4	0.2
GA	0.5	0.25	0.25
GD	1	0	0

2차 마코프 체인은 2차 표에 나타난 바와 같이 현재 상태와 이전 상태를 고려하여 도입할 수 있다.nth-order 체인은 특정 노트를 "그룹화"하는 경향이 있고, 다른 패턴과 시퀀스로 '분리'하는 경향이 있다.이러한 고차량의 체인들은 1차적인 시스템이 만들어내는 '무임한 방황'보다는 표현적 구조로 성과를 내는 경향이 있다.^[95]

마르코프 체인은 제나키스의 Analogique A와 B에서와 같이 구조적으로 사용될 수 있다.^[96]마르코프 체인은 음악 입력에 상호작용하기 위해 마르코프 모델을 사용하는 시스템에서도 사용된다.^[97]

보통 음악 시스템은 그들이 생성하는 유한 길이 시퀀스에 특정한 제어 제약 조건을 강제할 필요가 있지만, 제한된 메모리의 마르코프 가설을 위반하는 장거리 종속성을 유도하기 때문에 제어 제약조건은 마르코프 모델과 호환되지 않는다.이러한 한계를 극복하기 위해 새로운 접근법이 제안되었다.^[98]

야구

마르코프 체인 모델은 아직 사용이 드물지만, 1960년부터 선진 야구 분석에 이용되어 왔다.야구 경기의 각 하프닝은 주자와 아웃의 수를 고려할 때 마르코프 체인 상태에 적합하다.어느 타석에서도 아웃 수와 주자의 포지션 조합이 24개 가능하다.마크 판킨은 마코프 체인 모델이 팀뿐만 아니라 개인 선수 모두를 위해 만들어진 런을 평가하는 데 사용될 수 있다는 것을 보여준다.^[99]그는 또한 마코프 체인 모델이 번팅, 도루, 잔디 위에서 경기할 때 차이와 같은 게임 상황에 대한 통계를 분석하는 데 어떻게 이용되어 왔는지 등 다양한 전략과 경기 조건에 대해 논한다.아스트로터프.^[100]

마르코프 텍스트 생성기

마르코프 프로세스는 또한 샘플 문서가 주어진 표면적으로 실제처럼 보이는 텍스트를 생성하는 데 사용될 수 있다.마르코프 프로세스는 다양한 레크리에이션 "파로디 제너레이터" 소프트웨어에서 사용된다(분리된 언론, Jeff Harrison,^[101] Mark V 참조). 셰이니,^[102][103] 그리고 아카데미아스 중성자륨).The RiTa Toolkit을 포함하여 마르코프 체인을 사용하는 여러 오픈 소스 텍스트 생성 라이브러리가 존재한다.

확률론적 예측

마르코프 체인은 예를 들어 가격 동향,^[104] 풍력,^[105] 일조 강도와 같은 여러 분야에서 예측에 사용되어 왔다.^[106]마르코프 체인 예측 모델은 시계열 분석부터 ^[105]웨이블렛과 결합된 히든 마코프 모델,^[104] 마코프 체인 혼합물 분포 모델(MCM)까지 다양한 설정을 활용한다.^[106]

참고 항목

메모들

참조

외부 링크