최대 엔트로피 무작위 보행

MERW(Maximal Entropy Random Walk, MERW)는 그래프 상의 편향된 무작위 보행의 일반적인 유형으로, 최대 엔트로피의 원리에 따라 전환 확률을 선택하는데, 이는 지식의 현재 상태를 가장 잘 나타내는 확률 분포가 엔트로피가 가장 큰 분포라고 말한다.표준 랜덤 워크는 나가는 가장자리 사이의 모든 정점 균일한 확률 분포에 대해 선택하지만, 로컬 최대 엔트로피 비율을 MERW는 주어진 그래프에서 모든 경로 사이의 균일한 확률 분포를 가정하여 전체적으로(평균 엔트로피 생산) 최대화한다.

MERW는 과학의 다양한 분야에서 사용된다.직접 적용은 피보나치 부호화와 유사하게 제한된 채널을 통한 전송 속도를 최대화하기 위해 확률을 선택하는 것이다.그것의 속성은 링크 예측,^[2] 공동체 감지,^[3] 네트워크를^[4] 통한 강력한 전송 및 중앙집중성 조치와 ^[1]같은 복잡한 네트워크의 분석에서도 유용하게 만들었다.^[5]영상 분석에서도, 예를 들어, 시각적 편법 영역,^[6] 대상 지역화,^[7] 변조 탐지^[8] 또는 트랙토그래피 문제 등을 검출할 수 있다.^[9]

또한, 그것은 앤더슨 국산화처럼 확산 모델과 양자 예측 사이의 불일치를 복구하는 방법을 제안하면서 양자 역학의 몇 가지 특성을 재현한다.^[10]

기본 모델

Consider a graph with ${\displaystyle n}$ vertices, defined by an adjacency matrix ${\displaystyle A\in \left\{0,1\right\}^{n\times n}}$: ${\displaystyle A_{ij}=1}$ if there is an edge from vertex ${\displaystyle i}$ to ${\displaystyle j}$, 0 otherwise.단순성을 위해 대칭 $A{\displaystyle }$ ${\displaystyle A}$에 해당하는 비방향 그래프라고 가정한다$.$ 그러나 지시 및 가중 그래프에 대해서도 MERW를 일반화할 수 있다(예: 균일화 대신 경로 간에 볼츠만 분포).

우리는 이 그래프에서 무작위 보행을 마르코프 과정으로 선택하기를 원한다: 모든 꼭지점 $i{\displaystyle }$ ${\displaystyle i}$와 $j{\displaystyle }$ ${\displaystyle j}$로 나가는 가장자리에 대해$,$ $i{\displaystyle }$ ${\displaystyle$ i$}$을 방문한 후 이 가장자리를 사용하여 무작위로 보행기의 확률 $S{\displaystyle {}_{}}$ i ${\displaystyle j_{}}$ ${\$를 선택한다$.$ 정식으로.${\displaystyle S}$ ${\displaystyle S}($Markov 체인의 전환 확률을 포함) 다음과 같은 경우

• ${\displaystyle 0}$ ${\displaystyle \le }$ ${\displaystyle {}_{}}$ ${\displaystyle i_{}}$ ${\displaystyle j_{}}$ ${\displaystyle {}_{}}$ A ${\displaystyle i_{}}$ ${\displaystyle j_{}}$ ${\$ij}\leq A_{$ij}}$ 모든$$$$ $i{\displaystyle ,}$ ${\displaystyle j}$ ${\displaystyle$ i$,j}$ 및
• ${\displaystyle \sum _{}^{}}$ ${\displaystyle \underset{}{\overset{}{j}}}$= ${\displaystyle \underset{}{\overset{}{}}}$ ${\displaystyle \underset{}{\overset{}{}}{}_{}}$ ${\displaystyle i_{}}$ j${\displaystyle {}_{}}$= ${\displaystyle 1}$ ${\displaystyle \sum _{j=1}^{n}S_{ij}=1$} 모든 $i{\displaystyle }$ ${\displaystyle i}$에 대해$$$.$

이 그래프가 연결되어 있고 주기적이지 않다고 가정할 때, 에고다이컬 이론에 따르면 이 확률적 프로세스의 진화는 ${\displaystyle s}$S = ${\displaystyle \rho }$ ${\$displaystyle $\rho$ \rho }과$$ 같은 고정 확률 분포 $\rho {\displaystyle }$ ${\$$displaystyle \rho$ S$=\rho }$로 이어진다고 한다$.$

모든 정점에 Shannon 엔트로피를 사용하고 (엔트로피를 사용할 수 있도록) 이 정점을 방문할 확률에 대해 평균을 구하면 확률 프로세스의 평균 엔트로피 생산(엔트로피 비율)에 대해 다음과 같은 공식을 얻는다.

${\displaystyle H(S)=\sum _{i=1}^{n}\rho _{i}\sum _{j=1}^{n}S_{ij}\log(1/S_{ij}})}$

이 정의는 확률적 공정의 경로 공간에서 확률 분포의 점근 평균 엔트로피(길이당)와 동일한 것으로 밝혀졌다.

여기서 일반 무작위 보행(GRW)이라고 하는 표준 무작위 보행에서, 우리는 자연스럽게 각 발신 가장자리가 동등하게 발생가능하다는 것을 선택한다.

${\displaystyle {Si}_{}}$ ${\displaystyle j_{}}$= ${\displaystyle A\frac{{}_{}}{}}$ ${\displaystyle \frac{i_{}}{}}$ ${\displaystyle \frac{j_{}}{}}$ ${\displaystyle \frac{{}_{}}{\underset{}{\overset{}{}}}}$ ${\displaystyle \frac{\underset{}{\overset{}{k}}}{}}$= ${\displaystyle \frac{\underset{}{\overset{}{}}{}_{}}{}}$ ${\displaystyle \frac{i_{}}{}}$ ${\displaystyle \frac{k_{}}{}}$ ${\$ {$A_{ij}}{\sum \limits _{k=1}^{n}A_{$ik$\}\}\}\}\}\}\}\}\}\}.$

대칭 $A{\displaystyle }$ ${\displaystyle A}$의 경우 고정 확률 분포 $\rho {\displaystyle }$ ${\displaystyle \rho$}을$$(를) 유도하며,

$rho _{$$A_{ij}}{\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}}$$A_{ij$

모든 꼭지점에 대해 엔트로피 생산(${\displaystyle \mathrm{불확실성}}$)을 국소적으로 최대화하지만, 대개는 차선의 평균 글로벌 엔트로피 비율 $H{\displaystyle }$( S$){\displaystyle H(S)}$로 이어진다$.$

MERW는 $H{\displaystyle }$( $){\displaystyle H(S)}$를 최대화하는 확률적 행렬을 선택하거나$,$ 주어진 그래프에서 모든 경로 간에 균일한 확률 분포를 가정한다.Its formula is obtained by first calculating the dominant eigenvalue ${\displaystyle \lambda }$ and corresponding eigenvector ${\displaystyle \psi }$ of the adjacency matrix, i.e. the largest ${\displaystyle \lambda \in \mathbb {R} }$ with corresponding ${\displaystyle \psi \in \mathbb {R} ^{n}}$ s$\psi {\displaystyle }$ ${\displaystyle A}$= ${\displaystyle \lambda }$ ${\displaystyle \psi }${ {\$displaystyle \psi$A=\$lambda$ \$psi$ $\}.$ 그러면 확률적 행렬과 고정 확률 분포가 다음과 같이 주어진다.

${\displaystyle S_{ij}={\frac {A_{ij}}{\lambda }}{\frac {\psi _{j}{\psi _{i}}}}}}}{\frac {\frac}}{\psi}}}}}}}}}}}$

$i{\displaystyle }$ ${\displaystyle i}$ -th에서$$$$ $j{\displaystyle }$ ${\displaystyle j}$ -th$$ 꼭지점까지의 모든 가능한 $길이{\displaystyle }$ l$${\$displaystyle l}$의 모든 경로에 확률이 있음

${\displaystyle \frac{1}{}}$ ${\displaystyle \frac{{}^{}}{}}$ ${\displaystyle \frac{l^{}}{}}$ ${\displaystyle \frac{{}^{}}{}\frac{{}_{}}{}}$ ${\displaystyle \frac{j_{}}{}}$ ${\displaystyle \frac{{}_{}}{{}_{}}}$ ${\displaystyle \frac{i_{}}{}}$ ${\$ {1$}{\frac다 ^{$l}}{\$frac {\frac }{j}{j$}{\$propers _{i$

엔트로피 비율은 ${\displaystyle \mathrm{로그}}$ ${\displaystyle }$ (${\displaystyle \lambda }$ ) ${\displaystyle \log(\lambda )}$이고 고정 확률 분포 $\rho {\displaystyle }$ ${\displaystyle \rho }$은(는) 입니다$$.

${\displaystyle {\rho }_{}}$ ${\displaystyle i_{}}$= $ψ$ i ${\displaystyle \frac{{}_{}^{}}{{}_{}^{}}}$ ‖ ‖ 2 ${\displaystyle \frac{{\mathrm{}}_{}^{}}{}}$ $\$2 {\$displaystyle$ \$rho _{$i}={\frac {\$frac {\frac }^{i$}^{2$}}:{\\\$\ \$\{2$}^{2$\}\}.$

GRW와 대조적으로 MERW 전환 확률은 일반적으로 전체 그래프의 구조(비로컬)에 따라 달라진다.따라서 이러한 결정은 보행자가 직접 적용하는 것처럼 상상해서는 안 된다. 사람이 하는 것처럼 현지 상황에 따라 무작위로 보이는 결정이 이루어진다면 GRW 접근법이 더 적절하다.MERW는 최대 엔트로피의 원리에 기초하고 있어, 시스템에 대한 추가적인 지식이 없을 때 가장 안전한 가정으로 만든다.예를 들어, 그것은 입자와 같이 반드시 무작위적인 것이 아니라 복잡한 역학을 수행하는 물체에 대한 우리의 지식을 모델링하는 데 적합할 것이다.

파생의 스케치

단순성을 위해 고려된 그래프가 간접적이고, 연결되며, 페론-프로베니우스 정리로부터 지배적인 고유 벡터가 고유하다는 결론을 내릴 수 있다고 가정한다.Hence ${\displaystyle A^{l}}$ can be asymptotically (${\displaystyle l\rightarrow \infty }$) approximated by ${\displaystyle \lambda ^{l}\psi \psi ^{T}}$ (or ${\displaystyle \lambda ^{l} \psi \rangle \langle \psi }$ in bra–ket notation).

MERW는 경로를 따라 균일한 분포를 요구한다.중앙의$$ 길이 $2{\displaystyle \mathrm{}}$ ${\displaystyle l}$ ${\displaystyle 2l}$ 및$$ 꼭지점 $i{\displaystyle }$ ${\displaystyle i}$을(를) 가진 경로의$$ 숫자 $m{\displaystyle {}_{}}$ ${\displaystyle l_{}}$ ${\$은(는) 다음과 같다.

${\displaystyle m_{il}=\sum _{j=1}^n\sum _{k=1}^n{\left(A^l\right)}_{ji}{\left(A^l\right)}_{ik}\approx \sum _{j=1}^n\sum _{k=1}^n{\left({\lambda }^l\psi {\psi }^{\mathrm{\top }}\right)}_{ji}{\left({\lambda }^l\psi {\psi }^{\mathrm{\top }}\right)}_{ik}=\sum _{j=1}^n\sum _{k=1}^n{\lambda }^{2l}{\psi }_j{\psi }_i{\psi }_i{\psi }_k={\lambda }^{2l}{\psi }_i^2\underset{}{\underbrace{\sum _{j=1}^n{\psi }_j\sum _{k=1}^n{\psi }_k}}}$${\displaystyle m_{il}=\sum _{j=1}^{n}\sum _{k=1}^{n}\left(A^{l}\right)_{ji}\left(A^{l}\right)_{ik}\approx \sum _{j=1}^{n}\sum _{k=1}^{n}\left(\lambda ^{l}\psi \psi ^{\top }\right)_{ji}\left(\lambda ^{l}\psi \psi ^{\top }\right)_{ik}=\sum _{j=1}^{n}\sum _{k=1}^{n}\lambda ^{2l}\psi _{j}\psi _{i}\psi _{i}\psi _{k}=\lambda ^{2l}\psi _{i}^{2}$$\underbrace {\sum _{j=1}^{n}\reason$_${j}\sum$_{$k=1}^{n}\reason _{k}} _{=:b$

따라서 $모든{\displaystyle }$ i ${\displaystyle i}$에 대해$,$

${\displaystyle \rho _{i}=\lim _{l\rightarrow$$\infty }{\frac {m_{il}}{\sum \limits _{k=1}^{n}m_{kl}}}=\lim _{l\rightarrow \infty }{\frac {\lambda ^{2l}\psi _{i}^{2}b}{\sum \limits _{k=1}^{n}\lambda ^{2l}\psi _{k}^{2}b}}=\lim _{l\rightarrow \infty }{\frac {\psi _{i}^{2}}{\sum \limits _{k=1}^{n}\psi _{k}^{2}}}={\frac {\psi _{i}^{2}}{\sum \limits _{k=1}^{n}\psi _{k}^{2}}}={\frac {\psi _{i}^{2}}{$$\cHB \ _{$2}^{$2$

이후 두 정점에 대한 확률 분포를 유사하게 $계산$하며$,$ 하나는 i {\$displaystyle$ i} -th$$ 정점에 있을 확률을, 다음은 $j{\displaystyle }$ ${\displaysty j}$ -th$$ 정점에 있을 확률을 구한다.

${\frac {\psi}$$A_{ij}\psi _{j}}{{j}}{i'=1}^{n}\sum \limits _{j'=1}^{n}\psi _{i'}$$A_{i'j'}\psi _{j'}}={\frac {\psi _{i}$$A_{ij}\psi _{j}{\psi A\psi ^{\top }}={\frac {\psi _{i}$$A_{ij}\psi _{j}}{{$j}}{\$lambda \psi \$\{$2}^{2$

$i{\displaystyle }$ ${\displaystyle i}$ -th$$ 꼭지점에 있을 확률을 기준으로 나누면$,$ 즉 $i$ i$${\$displaystyle$j} -th$$$$ 꼭지점 다음에 $있는$ 조건부 $확률{\displaystyle {}_{}}$ ${\displaystyle S_{}}$ i ${\displaystyle j_{}}$${\$$displaystyle S_{ij}$가 된다.

${\displaystyle {Si}_{}}$ ${\displaystyle j_{}}$= ${\displaystyle A\frac{{}_{}}{}}$ i ${\displaystyle \frac{j_{}}{}}$ ${\displaystyle \lambda \frac{{}_{}}{}}$ ψ ${\displaystyle \frac{j_{}}{}}$ ${\displaystyle \frac{{}_{}}{{}_{}}}$ i {\$displaystyle S_{ij}={\frac {A_{ij}}{\lambda }}}}{\frac {\psi _{j$

가중 MERW: 볼츠만 경로 앙상블

MERW의 경우$$ 경로 간 균일한 앙상블에 해당하는 ${\displaystyle {Ai}_{}}$ ${\displaystyle j_{}}$ ${\displaystyle {}_{}}${ ${\displaystyle 0,}$ ${\displaystyle 1}$ ${\displaystyle \}}$ ${\displaystyle A_{ij}\in \{0$,1$\}$인 것으로 가정했다.However, the above derivation works for real nonnegative ${\displaystyle A}$. Parametrizing ${\displaystyle A_{ij}=\exp(-E_{ij})}$ and asking for probability of length ${\displaystyle l}$ path ${\displaystyle (\gamma _{0},\ldots ,\gamma _{l})}$, we get:

${\displaystyle {\textrm {Pr}}(\gamma _{0},\ldots ,\gamma _{l})=\rho _{\gamma _{0}}S_{\gamma _{0}\gamma _{1}}\ldots S_{\gamma _{l-1}\gamma _{l}}=\psi _{\gamma _{0}}{\frac {A_{\gamma _{0}\gamma _{1}}\ldots A_{\gamma _{l-1}\gamma _{l}}}{\lambda ^{l}}}\psi _{\gamma _{l}}=\psi _{\gamma _{0}}{\frac {\exp(-(E_{\gamma _{0}\gamma _{1}}+\ldots +E_{\gamma _{l-1}\cHB _{l})}}{\lambda ^{l}}\reason _{\reason _{l}}}$

볼츠만에서와 같이 주어진 경로에 $걸쳐$ ${\displaystyle {Ei}_{}}$ ${\displaystyle j_{}}$ ${\$의 합으로 정의되는 에너지 경로의 분포.예를 들어, Ising 모델에서 패턴의 확률 분포를 계산할 수 있다.

예

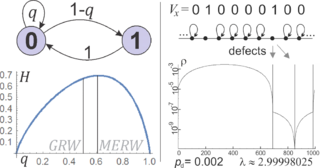
우선 간단한 비교 가능한 상황을 살펴보기로 하자.피보나치 부호화 - 0과 1의 순서로 메시지를 전송하고 싶지만, 두 개의 연속적인 1을 사용하지 않는 경우: 1이 지나면 0이 있어야 한다.그러한 순서로 전송되는 정보의 양을 최대화하기 위해, 우리는 이 제약을 충족하는 가능한 모든 시퀀스의 공간에서 균일한 확률 분포를 가정해야 한다.실제로 이렇게 긴 시퀀스를 사용하기 위해서는 1이 지나면 0을 사용해야 하지만 0이 지나면 0의 확률을 선택할 자유가 남아 있다.$이{\displaystyle }$ 확률을$q$ {\displaystyle $q}$로 나타내자$.$ 그러면 엔트로피 코딩은 이 선택된 확률 분포를 사용하여 메시지를 인코딩할 수 있을 것이다.The stationary probability distribution of symbols for a given ${\displaystyle q}$ turns out to be ${\displaystyle \rho =(1/(2-q),1-1/(2-q))}$. Hence, entropy production is ${\displaystyle H(S)=\rho _$$q{\displaystyle }$= (${\displaystyle 5}$- ${\displaystyle 1}$$)$${\displaystyle }$/ ${\displaystyle 2\approx }$ 0.${\displaystyle 130}$ ${\displaystyle q=({\sqrt{5}-1)/2\$ 약 $0.displaystyle$$q$=({\sqrt{5}-1)/2$\backslash$에 대해 최대화된 ${$0}\$log(1-q)+(1-q)\prig(오른쪽$$)}$에 대해 황금비로 알려져 있다.$이$와는 대조적으로, 표준 무작위 걷기는 차선의 $q{\displaystyle }$= 0.${\displaystyle q=0.5}$을(를$)$ 선택할 수 있다.$$큰 q {\$displaysty$q}을(를) 선택하면 0 이후 생성되는 정보의 양이 감소하지만$$, 그 후에는 1의 빈도도도도 감소하고, 그 후에는 어떤 정보도 쓸 수 없다.

더 복잡한 예로는 불량 1차원 순환 격자: 1000개의 노드가 링으로 연결되어 있으며, 결함을 제외한 모든 노드가 자체 루프(에지 자체)를 가지고 있다고 하자.표준 무작위 보행(GRW)에서 고정 확률 분포는 결함이 없는 정점의 확률의 2/3이 될 수 있다 – 국산화도 거의 없으며, GRW의 최소 한계인 표준 확산에 대해서도 유사하게 없다. MERW의 경우 인접 행렬의 지배적 고유 벡터를 먼저 찾아야 한다.다음에서$$ $\lambda {\displaystyle }$ ${\displaystyle \lambda }$을(를) Ximizing:

${\displaystyle(\lambda \psi )_{x}=(A\psi )_{x}=\psi _{x-1}+(1-V_{x})\psi _{x}+\x}{x}\psi _{x+1}.$

모든 위치 $x{\displaystyle }$ ${\displaystyle x}$에 대해$,$ 여기서 V ${\displaystyle x_{}}$= ${\displaystyle 1}$ 결함에 대한$$ V = 1 ${\displaystyle V_{x}=1},$ 그렇지 않으면 0.${\displaystyle {3\psi }_{}}$ x ${\$를 대체하고 방정식에$$ -1을 곱하면 다음과 같은 결과를 얻을 수 있다.

${\displaystyle E\psi _{x}=-(\psi _{x-1}-2\psi _{x}+\psi _{x+1}++++)++++V_{x}\psi _{x}}$

여기서 $E{\displaystyle }$= ${\displaystyle 3}$ -${\displaystyle \lambda }$ ${\displaystyle E=3-\lambda }$은(는) 이제 최소화되어$$ 에너지의 아날로그가 된다.브래킷 내부의 공식은 이산 라플라스 연산자로, 이 방정식을 고정 슈뢰딩거 방정식의 이산 아날로그식으로 만든다.양자역학에서와 마찬가지로 MERW는 확률분포가 (표준확산과는 대조적으로) 강하게 국부화된 밀도로 ${\displaystyle {with}_{}}$ x ${\displaystyle {}_{}}$ ${\displaystyle x_{}^{}}$ ${\displaystyle {}_{}^{}}$ x ${\displaystyle {\mathrm{}}_{}^{}}$ ${\$2}}의 양자지상 상태로 정확하게 이어져야 한다고 예측한다.Taking the infinitesimal limit, we can get standard continuous stationary (time-independent) Schrodinger equation (${\displaystyle E\psi =-C\psi _{xx}+V\psi }$ for ${\displaystyle C=\hbar ^{2}/2m}$) here.^[11]

참고 항목

• 최대 엔트로피의 원리
• 아이겐벡터 중심성
• 마르코프 체인
• 앤더슨 현지화

참조

외부 링크

• 가보르 시모니, Y 린, Z 장 "복잡한 네트워크에서 최대 엔트로피 무작위 도보 1차 통과 시간"2014년 사이언티픽 리포트.
• Maximal Entropy Random Wolfram 실증사업을 이용한 전자전도 모델