확률역학 초대칭 이론
Supersymmetric theory of stochastic dynamics확률론적 역학 또는 확률론(STS)의 초대칭 이론은 확률론적(부분적) 미분방정식(SDE)의 정확한 이론으로, 특히 노이즈가 있거나 없는 모든 연속 시간 동적 시스템을 포괄하는 가장 넓은 적용성을 가진 수학 모델의 등급이다. 물리적인 관점에서 본 이론의 주요 효용성은 지진이나 지진과 같은 순간적인 과정의 1/f, 깜박임, 균열 소음과 같은 현상과 같은 법칙 또는 Zipf의 법칙을 통해 여러 학문에 걸쳐 나타나는 유비쿼터스 자발적 장기적 역동적 행동에 대한 엄격한 이론적 설명이다. 신경아발렌치 수학적인 관점에서, STS는 수학적 물리학의 두 가지 주요 부분인 역동적인 시스템 이론과 위상학적 필드 이론을 연결시켜주기 때문에 흥미롭다. STS는 대수 위상, 초대칭장 이론 등 이와 관련되는 학문 외에도 전통적인 확률적 미분 방정식, 사이비-헤르미티아 연산자 이론과도 연결된다.
그 이론 BRST 게이지 조작 절차의 랑제방 SDEs,[1][2]은 나중에 고전 mechanics[3][4][5][6]과 그 확률 generalization,[7]higher-order 랑제방 SDEs,[8]와, 보다 최근, SDEs는 전송 사업자와 레의 개념에 BRST 형식 주의 연결할 수 있도록 임의의 form,[9]에 각색되었다에 신청서와 함께 시작했다.자발적인 breakdo 인식하다Wn 동적 혼돈의 확률적 일반화로서 BRST 초대칭의.
이 이론의 주요 개념은 궤도 대신, 미분형물의 SDE 정의 시간적 진화를 연구하는 것이다. 이러한 진화는 위상의 보존 및/또는 연속적 시간 역학에 의한 위상 공간의 근접성 개념을 나타내는 내적 BRST 또는 위상학적 초대칭이 있다. 그 이론은 모델을 일반화되고 확률적인 의미에서, 지상 상태가 초대칭이 아닌 경우, 즉 초대칭이 자연적으로 깨지는 경우, 혼돈된 것으로 식별한다. 이에 따라 항상 역동적인 혼란과 그 파생상품인 난기류, 자기조직적인 임계성을 동반하는 비상장기행동은 골드스톤 정리의 결과로 이해할 수 있다.
역사 및 다른 이론과의 관계
초대칭성과 확률적 역학 간의 최초의 관계 두 논문에서 1979년과 1982년 조르조 Parisi, 니콜라스 Sourlas,[1][2]는 N에서 BRST 게이지 조작 절차의 랑제방 SDEs, 즉,에 SDEs에 선형 위상 공간, 기울기 흐름 벡터 필드 및 첨가물 소음,며 신청서를 결과를 증명해 설립되었다=2 저녁밥을 먹다초대칭 모델. 그들의 일의 원래 목표였다차원 감소, 즉, 확증의 파인만 도표에서 특별한 취소 몇년 전 암논 Aharony, Yoseph Imry, Shang-keng Ma.[10]으로, 랑제방 SDEs의so-emerged 초대칭성:몇개의 물리적 개념 사이의[11][12][13][14][8]에 수립되어 있기 때문에 제안했다.그 fluctuatio를 포함하소산 이론, [14]자진스키 평등,[15] 현미경 가역성의 온사거 원리,[16] 포커-플랑크 방정식의 해결책,[17] 자기 조직화 [18]등.
고전역학,[3][4] 그것의 확률적 일반화,[7] 그리고 고차량의 랜지빈 SDE도[8] 초대칭 표현을 갖는다는 것을 확립하기 위해 유사한 접근법을 사용하였다. 그러나 실제의 역동적인 시스템은 결코 순수하게 랜지빈이나 고전적인 기계적인 것이 아니다. 또한, 물리적으로 의미 있는 Langevin SSE는 초대칭성을 자연적으로 깨지 않는다. 따라서 자발적인 초대칭이 역동적인 혼란으로 깨지는 것을 식별하기 위해서는 일반 형태의 SDE에 대한 파리-소라 접근법의 일반화가 필요하다. 이러한 일반화는 확률적 진화 연산자가 일반적인 경우 사이비-헤르미티아인이기 때문에 사이비-헤르미티아인 연산자[19] 이론의 엄밀한 공식화 뒤에야 나올 수 있었다. 그러한 일반화는[9] 모든 SDE가 N=1 BRST 또는 위상학적 초대칭(TS)을 가지고 있음을 보여주었고, 이 발견은 초대칭과 SDE 사이의 관계에 대한 이야기를 완성한다.
SSDE에 대한 BRST 절차 접근방식과 병행하여, 동적 시스템 이론에 종사하는 수학자들은 무작위 동적 시스템에 대해 정의된 일반화된 전송 연산자의 개념을 소개하고 연구하였다.[20][21] 이 개념은 확률적 진화 연산자인 STS의 가장 중요한 사물의 기초가 되며, 그 바탕에는 탄탄한 수학적 의미가 담겨 있다.
STS는 대수 위상과 밀접한 관계를 가지고 있으며 위튼형 위상학 또는 공생학장 이론으로 알려진 모델의 등급에 속한다.[22][23] [24][25][26][27] 초대칭 이론으로서, SSDE에 대한 BRST 절차 접근은 니콜라이 맵의 개념의 실현 중 하나로 볼 수 있다.[28][29]
랑게빈 SDE에 대한 파리-술라스 접근법
확률론적 역학에 대한 초대칭 접근법의 맥락에서, Langevin SDEs라는 용어는 유클리드 위상공간이 있는 X = {\X=\}n 그라데이션 흐름 벡터장 및 첨가 가우스 화이트 노이즈를 의미한다.
파리 소를라스 방법은 란제빈 SDE의 경로 일체형 표현을 구성하는 방법이다. Langevin SSDE를 게이지 조건으로 사용하는 BRST 게이지 고정 절차라고 생각할 수 있다. 즉, 다음과 같은 기능적 적분을 고려한다.
where denotes the r.h.s. of the Langevin SDE, is the operation of stochastic averaging with e 소음 구성의 정규 분포,
해당 기능파생물의 제이코비안(Jacobian)이며 경로 통합은 모든 폐쇄 경로(()= x (t){\ x(에 걸쳐 있다 여기서 과 t> 은 시간 진화의 초기 및 최종 순간이다.
치수축소
그 Parisi-Sourlas 건설은 원래"치수 감소"1976년에 암논 Aharony, Yoseph Imry고, 모든 주문 섭동 확장에, 단거리 교환과 무작위quenched 필드와d-dimensional(4<d<>6)시스템에서 중요한 위치를 밑이 사람의 것과 같다도 그것을 증명 Shang-keng 마는[10]이 제안한 목적을 두고 있다. 한(d–2)-di마그네틱 순수 [30]시스템 그들의 주장은 "임의의 경우를 위해 가장 앞서가는 단수 동작을 제공하는 파인만 다이어그램은 결합 요인과는 별개로, 순수한 경우를 위한 파인만 다이어그램과 2차원적으로 동일하다"[30]는 것을 나타냈다.
파리와 소렐라스... 가장 많은 적외선 분산형 다이어그램은 무작위 소스 삽입의 최대 수를 가진 다이어그램이며, 다른 다이어그램이 무시될 경우, 하나는 무작위 소스가 있는 곳에서 고전적 필드 이론에 대한 다이어그램 확장성을 남겨둔다는 것을 관찰했다.
그러자 파리시와 소렐라스는 무작위 시스템과 순수 시스템을 2차원 적은 차원으로 연결하는 근본적인 현상은 무작위 소스가 존재하는 고전적 장 이론이 2차원 적은 차원으로 해당 양자장 이론과 섭동적으로 동등하다는 점을 지적했다. Parisi와 Sourlas는 숨겨진 초대칭에 의한 치수 축소를 설명했다.[30]
위상학적 해석
파리-수라 건설의 위상학적 측면은 다음과 같은 방법으로 간략히 요약할 수 있다.[22] [31] 델타 기능, 즉 델타 기능의 무한대 수집은 Langevin SSDE의 솔루션만이 에 기여함을 보장한다 BRST 절차의 맥락에서 이러한 솔루션은 Grivov 복사본으로 볼 수 있다. 각 솔루션은 긍정적 또는 부정적 통합에 기여한다. with being the index of the so-called Nicolai map, , which in this case is the map from the space of closed paths in to the space of noise configurations, a map that provides a noise configuration at which a given closed path is a solution of the Langevin SDE. can be viewed as a realization of Poincaré–Hopf theorem on the infinite-dimensional space of close paths with the Langevin SDE playing the role of the vector field and with the solutions of Langevin SDE playing the role of the critical points with index . 은(는) 위상학적 특성이 있기 때문에 노이즈 구성과 무관하다. 그것은 그것의 확률적 평균인 에 대한 것과 동일하며 이것은 모델의 파티션 함수가 아니라 그것의 위튼 지수다.
경로 적분 표현
라그랑주 승수, }라는 추가 분야와Faddeev-Popov 유령이라고 하는 페르미오닉 분야 한 쌍의 되는 표준 분야 이론 기법의 도움으로 위튼 는 다음과 같은 형식을 취할 수 있다
where denotes collection of all the fields, p.b.c. stands for periodic boundary conditions, the so-called gauge fermion, , with and , and the BRST symmetry defined via its action on arbitrary functional as BRST 형식주의에서 (, 과 같은 Q-정확한 조각들은 게이지 고정 도구 역할을 한다 따라서 에 대한 경로 적분 식은 게이지 고정 용어 외에는 다른 작업이 포함되지 않는 모델로 해석할 수 있다. 이것은 위튼형 위상학장 이론의 결정적인 특징이며, 이 특별한 경우 SSDE에 대한 BRST 절차 접근법에서, BRST 대칭은 위상학적 초대칭으로도 인식될 수 있다.[22]
BRST 절차를 설명하는 일반적인 방법은 BRST 대칭이 게이지 변환의 페르미온 버전을 생성하는 반면, 경로 적분에 대한 전체적인 영향은 특정한 게이지 조건을 만족하는 구성으로만 통합을 제한하는 것이다. 이 해석은 궤적의 변형과 궤적 변환 및 게이지 조건의 역할을 각각 수행하는 Langevin SDE가 있는 Parisi-Sourlas 접근법에도 적용된다.
연산자 표현
고에너지 물리학과 응축 물질 모델의 물리적 페르미온은 시간 내에 항주기적 경계 조건을 가진다. 위튼 지수의 경로 적분 표현에서 페르미온에 대한 파격적인 주기적 경계 조건은 이 물체의 위상학적 성질의 기원이다. 이러한 경계 조건은 교환 기호 연산자로서 위튼 지수의 연산자 대표에 자신을 나타낸다.
힐베르트 공간
파동 기능은 ∈ X x X의 보소닉 변수뿐만 아니라 의 접선 공간으로부터 Grassmann 숫자 또는 페르미온의 함수인 X 그 wavefunctions X{X\displaystyle}에게 차별화된 형태로 fermions은 격차의 역할을 연기 χ 볼 수 있≡ d)∧{\displaystyle \chi \equiv dx\wedge}.[26]그 개념의 극미한 검색 엔진 최적화 generalizes은 Fokker–Planck 연산자, 본질적으로 검색 엔진 최적화 연기에서 최고의 미분 형식이 가지고 있는.나총 확률 분포의 분석. 최소 에서 낮은 수준의 차등 형식을 조건부 확률 분포로 해석할 수 있다.[32] 모든 각도의 미분 형태의 공간을 모델의 파장 기능으로 보는 것은 수학적 필요성이다. 그것이 없으면 모델의 가장 근본적인 개체인 파티션 함수인 위튼 지수는 존재하지 않을 것이고 역동적인 파티션 함수는 SDE의 고정 지점 수를 나타내지 않을 것이다(아래 참조). 파동 기능에 대한 가장 일반적인 이해는 궤도뿐만 아니라 미분 및/또는 랴푸노프 지수의 진화에 관한 정보를 포함하는 좌표가 없는 물체들이다.[33]
비선형 시그마 모형 및 대수 위상과의 관계
Ref에서는 위튼형 위상학장 이론의 하위 클래스인 [23]위상학적 비선형 시그마 모델(TNSM)의 1D 프로토타입으로 볼 수 있는 모델이 도입됐다.[26] 1D TNSM은 리만 위상 공간에 대해 정의되며, 유클리드 위상 공간에 대해서는 파리-술라스 모델로 축소된다. Its key difference from STS is the diffusion operator which is the Hodge Laplacian for 1D TNSM and for STS . This difference is unimportant in the context of relation between STS and algebraic topology, the relation established by t1D TNSM 이론(예: 참조).[26][22]
The model is defined by the following evolution operator , where with 이(가) 메트릭으로서 [ ^ ^ {\d}^{\}}}}}}은(는) 호지 라플라시안이며, 위상 공간의 외부 대수인 (의 차등은 파장치로 본다. 변환 H → = e / 2 e- U/ hat}}}}}{{}}}}, that brings the evolution operator to the explicitly Hermitian form = U= ^ -U/ = (/ - / ){\ 의 경우 U 은 N=2 초대칭 양자 역학의 해밀턴 사람이다. =( U+ d ) /2 / hat}}}{{{d}}}}}}}{{{\hat 및 2= U- ^ U )/ 2 / 2 }}}}}}}}}}}}}}}}}}}}}}}}}}{{{{{{{{{{{{{{{{{ U= = }^{2 은 H^ 및/또는 {\ {H의 스펙트럼이 실제적이고 음이 아님을 보여준다. 랜지빈 SDE의 SEO에게도 마찬가지다. 그러나 임의 형태의 SDE의 경우, 이는 더 이상 사실이 아니며, 이는 실제로 TS가 자연적으로 파괴될 수 있도록 하는 SEO의 고유값이 음수일 수도 있고 심지어 복잡할 수도 있기 때문이다.
1D TNSM 진화 연산자의 다음 특성은 임의 형태의 SDE의 SEO에도 적용된다. 진화 운영자는 미분형 수준의 운영자와 통근한다. As a result, , where and is the space of differential forms of degree . Furthermore, due to the presence of TS, , where are the supersymmetric eigenstates, , non-trivial in de Rham cohomology whereas the rest are the pairs of non-supersymmetric eigenstates of the form and . All supersymmetric eigenstates have exactly 0 고유값 및 우발 상황을 제외하고 모든 비대칭 상태는 0이 아닌 고유값을 갖는다. Non-supersymmetric pairs of eigenstates do not contribute to the Witten index, which equals the difference in the numbers of the supersymmetric states of even and odd degrees, For compact , 각 de Rham cohomology 클래스는 하나의 초대칭 고유 상태를 제공하며 Witten 지수는 위상 공간의 오일러 특성과 동일하다.
SDEs 임의의 형태의 BRST 절차이다.
The Parisi-Sourlas method of BRST procedure approach to Langevin SDEs have also been adapted to classical mechanics,[3] stochastic generalization of classical mechanics,[7] higher order Langevin SDEs,[8] and, more recently, to SDEs of arbitrary form.[9] 거기에 있는 동안는 색깔 있는 소음,higher-dimensional"기본 공간"부분 SDEs 등으로 설명하고 있는 모델을 고려할 수 있는 표준 기술 존재하며, STS의 핵심 요소 SDEs,의 다음과 같은 기본 클래스를 사용하여 논할 수 있다.
경로 적분 표현 및 Ito–Stratonovich 딜레마의 모호성.
BRST 게이지 조작 절차 랑제방 SDEs의 경우에서와 같은 방식으로 간다. 그 BRST 절차의 위상 해석은, 위튼 지표의 경로 적분 표현하는 게이지 페르미온,Ψ{\displaystyle\textstyle \Psi}, 같은 표정에 의해 결정된 정의는 하지만 d¯의 일반화된 버전과 같이 ı F−Θ ı e는(Q,ı e는){\textstyl 같다.E\textstyle{\bar{d}}=\imath _{F}-\Theta \imath _{e_{}}(Q,\imath_{e_{}})}. 한가지 중요한 섬세함 하지만 그 모델의 운영자 표현에 가는 길인 것 같다. 랑제방 SDEs, 고전 역학, 그리고 다른 SDEs 첨가물 소리를원과 달리finite-time 검색 엔진 최적화의 경로 적분 표현은 애매한 개체입니다. 이 모호성 momenta와 위치 사업자의 non-commutativity에서, 예를 들어, B^ x ^≠ x^ B^{\displaystyle{\hat{B}}{\hat{)}}\neq{\hat{)}}{\hat{B}}}. 그 결과, 경로 적분 표현에서 B(τ))(τ){B(\tau)x(\tau)\displaystyle}poss의 전체one-parameter 가족이 유래한다.어디 ψ(τ)⟩{\displaystyle \psi(\tau)\rangle}는 임의의 wavefunction을 나타내는 연산자 표현의 Ible 해석,(α B^)^+(1− α)x^ B^)ψ(τ)⟩{\displaystyle(\alpha{\hat{B}}{\hat{x}}+(1-\alpha){\hat{)}}{\hat{B}})\psi(\tau)\rangle},. 이에 따라 완전히 α -family 미소 SEOs,의{\displaystyle \alpha} 있다.
확률론적 역학의 경로 적분 표현은 확률론적 차이 방정식의 연속적인 시간 제한으로 SSE의 전통적인 이해와 동등하며, 여기서 매개변수 의 다른 선택을 SSE의 "해석"이라고 부른다. = / = 양자 이론에서 Weyl 대칭화 규칙으로 알려진 1/ = 에 선택은 스트라토노비치 해석으로 알려져 있다 양자론에서는 Weyl 대칭성이 해밀턴인의 은둔성을 보장하기 때문에 선호되는 반면, STS에서는 아래에서 논한 유한 시간 SEO의 가장 자연적인 수학적인 의미인 SSE 정의 차이점형성에 의해 유도된 확률 평균 풀백에 해당하기 때문에 Weyl-Stratonovic 접근법이 선호된다.
확률적 진화 연산자 계통
란제빈 SDEs의 SEO에 비해 일반 형태 SDE의 SEO는 사이비 헤르미티안이다.[19] 그 결과 비대칭 고유상태의 고유값은 실제 양성으로 제한되지 않는 반면, 초대칭 고유상태의 고유값은 여전히 정확히 0이다. Langevin SSDEs 및 비선형 시그마 모델과 마찬가지로, SEO의 아이겐스 시스템 구조는 위튼 지수의 위상학적 특성을 재정립한다: 비대칭적 고유상태의 비대칭적 쌍으로부터의 기여는 (폐쇄) 의 오일러 특성에 기여한다.ther properties of the SEO spectra is that and never break TS, i.e., 그 결과 오른쪽 그림에서 제시된 SEO 스펙트럼에는 크게 세 가지 유형이 있다. 고유값이 음(실제 부분)인 두 가지 유형은 자연적으로 파손된 TS에 해당한다. 모든 유형의 SEO 스펙트럼은 예를 들어 키네마틱 다이너모 이론과 STS 사이의 정확한 관계에서 확립될 수 있는 대로 실현 가능하다.[34]
BRST 절차 미포함 S
확률적 진화 연산자의 수학적 의미
유한 시간 SEO는 BRST 게이지 고정 절차를 거치지 않고 차동 형태에 대한 SSE 유도 작용을 직접 연구한다는 생각에 기초하여 다른, 보다 수학적 방법으로 얻을 수 있다. 그렇게 관측된 유한 시간 SEO는 일반화된 전송 연산자로[20][21] 동적 시스템 이론에서 알려져 있으며, SDE의 고전적 이론(예: 참조)[35][36]에서도 사용되었다(예: 참조). STS로부터의[9] 이 구성에 대한 기여는 SDE에 대한 BRST 절차와의 관계를 확립하고 이를 근간으로 하는 초대칭 구조의 표현이다.
Namely, for any configuration of the noise, , and an initial condition, , SDE defines a unique solution/trajectory, . Even for noise configurations that are non-differentiable with respect to time, 솔루션은 초기 조건과 관련하여 차별화 함, x{{\ x[37] 즉, SDE는 위상 공간의 소음 구성 의존적 차이점 유형들의 패밀리를 자체적으로 정의하며, : → 이 물체는 소음 구성에 의존하는 모든 궤도의 집합 및/또는 정의로 이해할 수 있다. ( )= ( ) x. 차이점형식은 동작이나 풀백을 유도하며, :( )→ ( X) . Unlike, say, trajectories in , pullbacks are linear objects even for nonlinear . Linear objects can be averaged and averaging over the noise configurations, , results in the finite-time SEO which is unique and corresponds to the Weyl-Stratonovich interpretation of the BRST procedure approach to SDEs, .
이러한 유한시간 SEO의 정의 안에서 위튼지수는 일반화된 이전사업자의 날카로운 흔적으로 인식될 수 있다.[20][21] It also links the Witten index to the Lefschetz index, x는 폐쇄) 위상 공간의 오일러 특성과 동일한 위상수다. Namely, .
초대칭의 의미와 나비효과
Langevin SSDE의 N=2 초대칭은 현미경[16] 가역성과 자진스키 평등의 Onsager 원리와 연결되어 있다.[15] 고전역학에서는 해당 N=2 초대칭과 인간성 사이의 관계가 제안되었다.[6] 일반적으로 물리적 인수가 적용되지 않을 수 있는 SSE 형식에서는 TS에 대한 하위 수준의 설명을 사용할 수 있다. 이 설명은 유한 시간 SEO를 SSDE 정의 차이점 유형의 확률 평균 풀백으로 이해하는 것에 기초한다(위 항 참조). 이 그림에서, 왜 어떤 SSE가 TS를 가지고 있는지에 대한 질문은 왜 외부 파생상품이 어떤 차이점형주의의 후퇴와 통용되는가에 대한 질문과 같다. 이 질문에 대한 답은 해당 지도의 차별성이다. 즉, TS의 존재는 연속시간 흐름이 의 연속성을 보존한다는 문장의 대수적 버전이다 초기에는 두 개의 근접점이 진화 중에도 근접하게 유지될 것이며, 은 M 이 차이점이라고 하는 또 다른 방법일 뿐이다.
결정론적 혼란 모델에서 초기 근접점은 무한히 긴 시간적 진화의 한계에 속할 수 있다. 이것은 유명한 나비효과로, 에서 Mt t t{\{tt이(가) 차별성을 잃는다는 말과 맞먹는다. 역학의 대수적 표현에서 무한히 긴 시간 한계에서의 진화는 SEO의 지상 상태로 설명되며 나비 효과는 TS의 자연 분해 즉, 지상 상태가 초대칭이 아닌 상황에 해당된다. 주목할 점은, 결정론적 혼란 역학에 대한 전통적인 이해와는 달리, TS의 자발적 파괴는 확률적 사례에도 작용한다. 결정론적 역학은 사실 수학적 이상화이기 때문에 이것이 가장 중요한 일반화다. 실제 동적 시스템은 그들의 환경으로부터 격리될 수 없으며 따라서 항상 확률적인 영향을 받는다.
자발적 초대칭 파괴 및 동적 혼란
SSDE에 적용된 BRST 게이지 고정 절차는 위튼 지수로 직접 이어진다. 위튼 지수는 위상학적 성격을 띠고 있으며 어떤 동요에도 반응하지 않는다. 특히 위튼 지수를 사용하여 계산한 모든 반응 상관자는 사라진다. 이 사실은 STS 내에서 물리적인 해석을 가지고 있다: 위튼 지수의 물리적 의미는 소음의[32] 분할 기능이며, 동적 시스템에서 소음까지 역작용이 없기 때문에 위튼 지수는 SDE의 세부사항에 대한 정보를 가지고 있지 않다. 이와는 대조적으로, 모델의 세부사항에 관한 정보는 이론의 다른 추적과 같은 대상인 동적 파티션 함수에 포함되어 있다.
광범위한 모델의 경우 동적 파티션 함수는 SDE 정의 차이점 유형의 확률 평균 고정점 수에 대한 하한을 제공한다.
자발적인 TS 파괴를 역동적인 혼돈의 개념의 확률적인 일반화로 보아야 하는 이유의 전체 목록은 다음과 같다.
- 양성 다이나믹 엔트로피.
- 골드스톤의 정리에 따르면 자발적인 TS 파괴는 반드시 장거리의 역동적 행동을 맞춤화해야 하는데, 그 발현 중 하나는 TS의 의미 맥락에서 위에서 논의한 나비효과다.
- SEO의 아이겐스시스템 속성에서 TS는 한 3 {\ 3만 자연적으로 깨질 수 있다 이러한 결론은 결정론적 혼돈에 대한 푸앵카레-벤디슨 정리의 확률적 일반화로 볼 수 있다.
- 결정론적 사례에서 동적 의 관점에서 통합 가능한 모델은 F 의 글로벌 안정적이고 불안정한 다지관을 가지고 있다 이러한 모델의 글로벌 지상 상태의 브래지어/케트는 글로벌 안정/불안정 다지관의 푸앵카레 듀얼이다. 이러한 접지 상태는 초대칭이므로 TS가 자연적으로 파손되지 않는다. 반대로 모델이 비통합적이거나 혼돈적일 때, 그 글로벌(비)안정적인 다지관은 잘 정의된 위상학적 다지관이 아니라, 오히려 분기 다지관의 개념을 이용하여 포착할 수 있는 프랙탈적이고 자기반복적인 구조를 갖게 된다.[38] 그러한 다지관을 나타낼 수 있는 파동은 초대칭이 될 수 없다. 그러므로 TS파괴는 본질적으로 역동적인 시스템의 의미에서의 비통합성의 개념과 관련이 있는데, 이것은 사실 결정론적 혼돈에 대한 또 다른 널리 받아들여진 정의다.
위와 같은 TS 파괴 작업의 모든 특징은 결정론적 모델과 확률론적 모델 모두를 위한 것이다. 이는 위상학적 혼합과 같은 궤적 기반 특성을 원칙적으로 확률론적 사례로 일반화할 수 없는 전통적인 결정론적 혼돈과는 대조적이다. 왜냐하면 양자역학에서와 마찬가지로 모든 궤적이 소음의 존재에서 가능하기 때문이다. 예를 들어 위상학적 혼합 속성은 모든 모자에 의해 사소한 것으로 만족되기 때문이다.잡음 강도가 0이 아닌 범위
위상학장 이론으로서의 STS
STS의 위상학 분야는 위튼형 위상학 분야 이론의 일원으로 인정받을 수 있다.[22][23][25][26][27] 즉, STS의 일부 물체는 위튼 지수가 가장 유명한 예인 만큼 위상학적 성격을 띠고 있다. 다른 종류의 위상학적 사물들이 있다. 한 등급의 물체는 인스턴트온, 즉 과도역학과 관련이 있다. 종이가 구겨지고, 단백질이 접히는 것, 그리고 다른 많은 비선형적인 동적 과정, 즉 외부적인 (돌연한) 매개변수의 변화에 대응한 것은 인스턴트 원학적 역동성으로 인식될 수 있다. 수학적인 관점에서 볼 때, 인스턴트온은 결정론적 운동 방정식인 = 의 덜 안정적인 고정점에서 보다 안정적인 으로 이어지는 해결책의 집합이다 인스턴트온에서 계산된 특정 매트릭스 원소는 위상학적 성격을 띤다. 이러한 행렬 요소의 예는 임계점 및 에 대해 정의될 수 있으며 은(는) 보다 안정적이다
위의 인스턴트 매트릭스 요소는 결정론적 한계에서만 정확하다. In the general stochastic case, one can consider global supersymmetric states, 's, from the De Rham cohomology classes of and observables, , that are Poincare duals of closed manifolds non-trivial in homology of . The following matrix elements, are topological invariants representative of the structure of De Rham coho X의 mology 링
적용들
초대칭 이론의 확률 역학은 다른 방식으로 흥미로워질 수 있다. 예를 들어, STS는 초대칭 개념의 유망한 실현을 제공한다. 일반적으로 초대칭의 맥락에서 크게 두 가지 문제가 있다. 첫 번째는 이 수학적인 실체와 실제 세계 사이에 연결을 설정하는 것이다. STS 내에서 초대칭은 모든 연속 시간 동적 시스템에 관련되기 때문에 자연에서 가장 일반적인 대칭이다. 두 번째는 초대칭의 자발적 붕괴다. 이 문제는 입자물리학에 특히 중요한데, 극히 짧은 스케일로 존재하는 경우, 초입자의 초대칭이 대규모로 자연적으로 깨져야 하기 때문이다. 이 문제는 초대칭이 자연적으로 끊기 어렵기 때문에 비교가 안 되는데, 이는 소프트 또는 명시적으로 초대칭이 깨지는 바로 그 배경이다.[39] STS 내에서, 초대칭의 자발적 파괴는 실제로 혼돈, 난류, 자기 조직적 임계 등으로 여러 분야에 걸쳐 다양하게 알려져 있는 비경쟁적 역동적 현상이다.
STS의 몇 가지 더 구체적인 적용은 다음과 같다.
확률역학 분류
STS는 TS의 파손 여부와 유량 벡터장의 통합성에 따라 확률적 모델에 대한 분류를 제공한다. 인은 혼돈의 경계에 있는 일반 위상 다이어그램의 일부로 예시될 수 있다(오른쪽 그림 참조). 위상 다이어그램에는 다음과 같은 속성이 있다.
- 물리적 모델의 경우 TS는 결국 소음 강도의 증가와 함께 복원된다.
- 대칭 위상은 지상 상태가 정상 상태 총 확률 분포의 초대칭 상태이기 때문에 열 평형 또는 T 위상이라고 할 수 있다.
- 결정론적 한계에서 순서 단계는 통합할 수 없는 흐름과 함께 결정론적 혼란 역학과 동일하다.
- 순서가 정해진 비통합 페이즈는 통상적인 결정론적 혼란이 그 안에 속하기 때문에 혼돈 또는 C 페이즈라고 할 수 있다.
- 순서가 지정된 통합 가능 위상은 결정론적 한계에서 사라지기 때문에 소음 유발 혼돈 또는 N 위상이라고 할 수 있다. TS는 (안티)인스턴트의 응축에 의해 파손된다(아래 참조).
- 더 강한 소음에서 날카로운 N-C 경계는 (반)인스턴트들이 그들의 개성을 잃고 외부 관찰자가 한 터널링 과정을 다른 것과 구별하기 어렵기 때문에 크로스오버로 얼룩져야 한다.
자기조직적 중요성 평가절하
크래킹 소음과 같은 자연에서의 많은 갑작스러운 (또는 인스턴트) 과정은 Zipf의 법칙이라고 불리는 무규모 통계를 나타낸다. 이 독특한 자발적 역동적 행동에 대한 설명으로서, 일부 확률적 역동적 시스템이 스스로 임계점, 즉 자기조직적 임계점(SOC)으로 알려진 현상학적 접근방식을 갖는 경향이 있다고 믿는 것이 제안되었다.[40] STS는 이 현상에 대한 대안적인 관점을 제공한다.[41] STS 내에서 SOC는 N상에서의 역학관계에 지나지 않는다. 구체적으로는 N상(N상)의 결정적인 특징은 TS파단(Ts breaking)의 독특한 메커니즘이다. 흐름의 비통합성에 의해 TS가 깨지는 C상과는 달리, N상에서는 인스턴트온과 소음 유발 안티인스턴트의 구성의 응축, 즉 시간역전 인스턴트온으로 인해 TS가 자연적으로 깨진다. 이러한 프로세스는 예를 들어 서로 다른 유인 장치 사이의 소음으로 인한 터널링 이벤트로 대략 해석할 수 있다. 질적으로 N상에서의 역학관계는 골드스톤 정리의 결과로서 스케일 프리 행동/통계를 나타내야 하는 갑작스러운 점프나 "어발렌치"의 시퀀스로 외부 관찰자에게 나타난다. N상에서의 역학의 이 그림은 바로 SOC의 개념이 설명하기 위해 고안된 역동적인 행동이다. SOC에 대한 원래 이해와는 대조적으로,[42] STS의 해석은 스케일 프리 동작이 리노말화 그룹 흐름의 불안정한 고정점과 연관되어 있는 전통적인 임계 현상 이론과는 거의 관계가 없다.
키네마틱 다이너모 이론
키네마틱 다이너모의 자기유체역학 현상도 TS의 자발적 파괴로 확인할 수 있다.[34] 이 결과는 자기장의 진화 연산자와 배경 물질의 흐름을 설명하는 해당 SDE의 SEO 사이의 동등함에서 나타난다. 따라서 등장한 STS-키네마틱 다이너모드 대응은 특히 가장 빠르게 성장하는 고유모드의 두 유형을 모두 가진 키네마틱 다이너모가 알려져 있기 때문에 실제와 복잡한 지면 상태 고유값을 사용하여 두 가지 유형의 TS 파괴 스펙트럼이 가능하다는 것을 입증한다.[43]
과도역학
Quench와 같은 다양한 형태의 과도적 역학이 자발적인 장거리 행동을 보인다는 것은 잘 알려져 있다. 위상 전환에 걸쳐 진동이 발생하는 경우, 이러한 행동은 종종 임계도의 근접성에 기인한다. 위상 전환을 나타내지 않는 쿼치도 장거리 특성을 보이는 것으로 알려져 있는데, 가장 잘 알려진 예는 바크하우젠 효과와 크래킹 소음 개념의 다양한 실현이다. Quench에서 스케일 프리 동작에 대한 이론적 설명은 위상 전환의 발생 여부에 관계없이 모든 쿼치에 대해 동일해야 한다는 것이 직관적으로 호소한다. STS는 그러한 설명을 제공한다. 즉, 과도역학은 본질적으로 복합적인 인스턴트온이고 TS는 본질적으로 인스턴트온 내에서 깨진다. 비록 인스턴트온 내에서 TS가 끊어지는 것은 정확히 지구 지상 상태에 의한 대칭의 자발적 파괴 현상에 기인하지는 않지만, 이러한 효과적인 TS 끊기는 또한 스케일 프리 동작을 야기해야 한다. 이러한 이해는 응축된 인스턴스(instance)가 상관 함수에서 로그의 출현으로 이어진다는 사실에 의해 뒷받침된다.[44] 이 과도기적 역학의 그림은 디지털 메모리 컴퓨팅 기계의 계산 효율을 설명한다.[45]
저에너지 효율적 이론으로 역동적 혼돈에 대비
물리학에서 자발적 대칭 파괴는 "순서"라고 알려져 있다. 예를 들어, 액체에서 변환 대칭의 자발적 분해는 결정화의 수학적인 본질 또는 분자의 격자 내 공간적 "순서화"이다. 그러므로 혼란스러운 역학의 자발적인 TS파쇄 그림은 어떤 의미에서 "chaos"라는 단어의 의미론과는 반대되는 것이다. 시간적 특성 때문에 TS파괴질서에 가장 근접한 원시 그리스 신으로 보이는 것은 사실 혼돈이 아니라 크로노스다. 앞으로 TS파쇄를 위해 "chaos"보다 더 정확한 식별자가 만들어져야 할지도 모른다. 이 순간 현재, 역동적인 혼란에 대한 질적으로 새로운 이해는 이미 난류나 신경 역학 같은 몇몇 중요한 문제들의 해결로 이어질 수 있는 연구 방향을 가리키고 있다. 즉, 다른 "주문"의 경우와 마찬가지로, 주문 매개변수에 대한 저에너지 유효 이론의 관점에서 혼돈 역학에 대한 단순하면서도 정확한 설명을 달성할 수 있다. 혼돈 역학에 대한 저 에너지 유효 설명은 매우 사례별로 구체적일 수 있지만, 주문 매개변수는 항상 자연적으로 파손된 TS의 갭 없는 페르미온 또는 골드스티노를 대표해야 한다.
참고 항목
참조
- ^ a b Parisi, G.; Sourlas, N. (1979). "Random Magnetic Fields, Supersymmetry, and Negative Dimensions". Physical Review Letters. 43 (11): 744–745. Bibcode:1979PhRvL..43..744P. doi:10.1103/PhysRevLett.43.744.
- ^ a b Parisi, G. (1982). "Supersymmetric field theories and stochastic differential equations". Nuclear Physics B. 206 (2): 321–332. Bibcode:1982NuPhB.206..321P. doi:10.1016/0550-3213(82)90538-7.
- ^ a b c Gozzi, E.; Reuter, M. (1990). "Classical mechanics as a topological field theory". Physics Letters B. 240 (1–2): 137–144. Bibcode:1990PhLB..240..137G. doi:10.1016/0370-2693(90)90422-3.
- ^ a b Niemi, A. J. (1995). "A lower bound for the number of periodic classical trajectories". Physics Letters B. 355 (3–4): 501–506. Bibcode:1995PhLB..355..501N. doi:10.1016/0370-2693(95)00780-o.
- ^ Niemi, A. J.; Pasanen, P. (1996-10-03). "Topological σ-model, Hamiltonian dynamics and loop space Lefschetz number". Physics Letters B. 386 (1): 123–130. arXiv:hep-th/9508067. Bibcode:1996PhLB..386..123N. doi:10.1016/0370-2693(96)00941-0. S2CID 119102809.
- ^ a b Gozzi, E.; Reuter, M. (1989-12-28). "Algebraic characterization of ergodicity". Physics Letters B. 233 (3): 383–392. Bibcode:1989PhLB..233..383G. doi:10.1016/0370-2693(89)91327-0.
- ^ a b c Tailleur, J.; Tănase-Nicola, S.; Kurchan, J. (2006-02-01). "Kramers Equation and Supersymmetry". Journal of Statistical Physics. 122 (4): 557–595. arXiv:cond-mat/0503545. Bibcode:2006JSP...122..557T. doi:10.1007/s10955-005-8059-x. ISSN 0022-4715. S2CID 119716999.
- ^ a b c d Kleinert, H.; Shabanov, S. V. (1997-10-27). "Supersymmetry in stochastic processes with higher-order time derivatives". Physics Letters A. 235 (2): 105–112. arXiv:quant-ph/9705042. Bibcode:1997PhLA..235..105K. doi:10.1016/s0375-9601(97)00660-9. S2CID 119459346.
- ^ a b c d Ovchinnikov, I. V. (2016-03-28). "Introduction to Supersymmetric Theory of Stochastics". Entropy. 18 (4): 108. arXiv:1511.03393. Bibcode:2016Entrp..18..108O. doi:10.3390/e18040108. S2CID 2388285.
- ^ a b Aharony, A.; Imry, Y.; Ma, S.K. (1976). "Lowering of dimensionality in phase transitions with random fields". Physical Review Letters. 37 (20): 1364–1367. doi:10.1103/PhysRevLett.37.1364.
- ^ Cecotti, S; Girardello, L (1983-01-01). "Stochastic and parastochastic aspects of supersymmetric functional measures: A new non-perturbative approach to supersymmetry". Annals of Physics. 145 (1): 81–99. Bibcode:1983AnPhy.145...81C. doi:10.1016/0003-4916(83)90172-0.
- ^ Zinn-Justin, J. (1986-09-29). "Renormalization and stochastic quantization". Nuclear Physics B. 275 (1): 135–159. Bibcode:1986NuPhB.275..135Z. doi:10.1016/0550-3213(86)90592-4.
- ^ Dijkgraaf, R.; Orlando, D.; Reffert, S. (2010-01-11). "Relating field theories via stochastic quantization". Nuclear Physics B. 824 (3): 365–386. arXiv:0903.0732. Bibcode:2010NuPhB.824..365D. doi:10.1016/j.nuclphysb.2009.07.018. S2CID 2033425.
- ^ a b Kurchan, J. (1992-07-01). "Supersymmetry in spin glass dynamics". Journal de Physique I. 2 (7): 1333–1352. Bibcode:1992JPhy1...2.1333K. doi:10.1051/jp1:1992214. ISSN 1155-4304. S2CID 124073976.
- ^ a b Mallick, K.; Moshe, M.; Orland, H. (2007-11-13). "Supersymmetry and Nonequilibrium Work Relations". arXiv:0711.2059 [cond-mat.stat-mech].
- ^ a b Gozzi, E. (1984). "Onsager principle of microscopic reversibility and supersymmetry". Physical Review D. 30 (6): 1218–1227. Bibcode:1984PhRvD..30.1218G. doi:10.1103/physrevd.30.1218.
- ^ Bernstein, M. (1984). "Supersymmetry and the Bistable Fokker-Planck Equation". Physical Review Letters. 52 (22): 1933–1935. Bibcode:1984PhRvL..52.1933B. doi:10.1103/physrevlett.52.1933.
- ^ Olemskoi, A. I; Khomenko, A. V; Olemskoi, D. A (2004-02-01). "Field theory of self-organization". Physica A: Statistical Mechanics and Its Applications. 332: 185–206. Bibcode:2004PhyA..332..185O. doi:10.1016/j.physa.2003.10.035.
- ^ a b Mostafazadeh, A. (2002-07-19). "Pseudo-Hermiticity versus PT-symmetry III: Equivalence of pseudo-Hermiticity and the presence of antilinear symmetries". Journal of Mathematical Physics. 43 (8): 3944–3951. arXiv:math-ph/0203005. Bibcode:2002JMP....43.3944M. doi:10.1063/1.1489072. ISSN 0022-2488. S2CID 7096321.
- ^ a b c Reulle, D. (2002). "Dynamical Zeta Functions and Transfer Operators" (PDF). Notices of the AMS. 49 (8): 887.
- ^ a b c Ruelle, D. (1990-12-01). "An extension of the theory of Fredholm determinants". Publications Mathématiques de l'Institut des Hautes Études Scientifiques. 72 (1): 175–193. doi:10.1007/bf02699133. ISSN 0073-8301. S2CID 121869096.
- ^ a b c d e Birmingham, D; Blau, M.; Rakowski, M.; Thompson, G. (1991). "Topological field theory". Physics Reports. 209 (4–5): 129–340. Bibcode:1991PhR...209..129B. doi:10.1016/0370-1573(91)90117-5.
- ^ a b c Witten, E. (1988-09-01). "Topological sigma models". Communications in Mathematical Physics. 118 (3): 411–449. Bibcode:1988CMaPh.118..411W. doi:10.1007/BF01466725. ISSN 0010-3616. S2CID 34042140.
- ^ Baulieu, L.; Singer, I.M. (1988). "The topological sigma model". Communications in Mathematical Physics. 125 (2): 227–237. doi:10.1007/BF01217907. S2CID 120150962.
- ^ a b Witten, E. (1988-09-01). "Topological quantum field theory". Communications in Mathematical Physics. 117 (3): 353–386. Bibcode:1988CMaPh.117..353W. doi:10.1007/BF01223371. ISSN 0010-3616. S2CID 43230714.
- ^ a b c d e Witten, E. (1982). "Supersymmetry and Morse theory". Journal of Differential Geometry. 17 (4): 661–692. doi:10.4310/jdg/1214437492. ISSN 0022-040X.
- ^ a b Labastida, J. M. F. (1989-12-01). "Morse theory interpretation of topological quantum field theories". Communications in Mathematical Physics. 123 (4): 641–658. Bibcode:1989CMaPh.123..641L. CiteSeerX 10.1.1.509.3123. doi:10.1007/BF01218589. ISSN 0010-3616. S2CID 53555484.
- ^ Nicolai, H. (1980-12-22). "Supersymmetry and functional integration measures". Nuclear Physics B. 176 (2): 419–428. Bibcode:1980NuPhB.176..419N. doi:10.1016/0550-3213(80)90460-5.
- ^ Nicolai, H. (1980-01-28). "On a new characterization of scalar supersymmetric theories" (PDF). Physics Letters B. 89 (3): 341–346. Bibcode:1980PhLB...89..341N. doi:10.1016/0370-2693(80)90138-0.
- ^ a b c Klein, A.; Landau, L.J.; Perez, J.F. (1984). "Supersymmetry and the Parisi-Sourlas dimensional reduction: a rigorous proof". Communications in Mathematical Physics. 94 (4): 459–482. doi:10.1007/BF01403882.
- ^ Baulieu, L.; Grossman, B. (1988). "A topological interpretation of stochastic quantization". Physics Letters B. 212 (3): 351–356. Bibcode:1988PhLB..212..351B. doi:10.1016/0370-2693(88)91328-7.
- ^ a b Ovchinnikov, I.V. (2013-01-15). "Topological field theory of dynamical systems. II". Chaos: An Interdisciplinary Journal of Nonlinear Science. 23 (1): 013108. arXiv:1212.1989. Bibcode:2013Chaos..23a3108O. doi:10.1063/1.4775755. ISSN 1054-1500. PMID 23556945. S2CID 34229910.
- ^ Graham, R. (1988). "Lyapunov Exponents and Supersymmetry of Stochastic Dynamical Systems". EPL. 5 (2): 101–106. Bibcode:1988EL......5..101G. doi:10.1209/0295-5075/5/2/002. ISSN 0295-5075.
- ^ a b Ovchinnikov, I.V.; Ensslin, T. A. (2016). "Kinematic dynamo, supersymmetry breaking, and chaos". Physical Review D. 93 (8): 085023. arXiv:1512.01651. Bibcode:2016PhRvD..93h5023O. doi:10.1103/PhysRevD.93.085023. S2CID 59367815.
- ^ Ancona, A.; Elworthy, K. D.; Emery, M.; Kunita, H. (2013). Stochastic differential geometry at Saint-Flour. Springer. ISBN 9783642341700. OCLC 811000422.
- ^ Kunita, H. (1997). Stochastic flows and stochastic differential equations. Cambridge University Press. ISBN 978-0521599252. OCLC 36864963.
- ^ Slavík, A. (2013). "Generalized differential equations: Differentiability of solutions with respect to initial conditions and parameters". Journal of Mathematical Analysis and Applications. 402 (1): 261–274. doi:10.1016/j.jmaa.2013.01.027.
- ^ Gilmore, R.; Lefranc, M. (2011). The topology of chaos : Alice in stretch and squeezeland. Wiley-VCH. ISBN 9783527410675. OCLC 967841676.
- ^ Chung, D. J. H.; Everett, L. L.; Kane, G. L.; King, S. F.; Lykken, J.; Wang, Lian-Tao (2005-02-01). "The soft supersymmetry-breaking Lagrangian: theory and applications". Physics Reports. 407 (1–3): 1–203. arXiv:hep-ph/0312378. Bibcode:2005PhR...407....1C. doi:10.1016/j.physrep.2004.08.032. S2CID 119344585.
- ^ Watkins, N. W.; Pruessner, G.; Chapman, S. C.; Crosby, N. B.; Jensen, H. J. (2016-01-01). "25 Years of Self-organized Criticality: Concepts and Controversies". Space Science Reviews. 198 (1–4): 3–44. arXiv:1504.04991. Bibcode:2016SSRv..198....3W. doi:10.1007/s11214-015-0155-x. ISSN 0038-6308. S2CID 34782655.
- ^ Ovchinnikov, I. V. (2016-06-01). "Supersymmetric Theory of Stochastics: Demystification of Self-Organized Criticality". In Skiadas C.H. and Skiadas C. (ed.). Handbook of Applications of Chaos Theory. Chapman and Hall/CRC. pp. 271–305. doi:10.1201/b20232. ISBN 9781466590441.
- ^ Bak, P.; Tang, C.; Wiesenfeld, K. (1987). "Self-organized criticality: An explanation of the 1/f noise". Physical Review Letters. 59 (4): 381–384. Bibcode:1987PhRvL..59..381B. doi:10.1103/PhysRevLett.59.381. PMID 10035754.
- ^ Bouya, I.; Dormy, E. (2013-03-01). "Revisiting the ABC flow dynamo". Physics of Fluids. 25 (3): 037103–037103–10. arXiv:1206.5186. Bibcode:2013PhFl...25c7103B. doi:10.1063/1.4795546. ISSN 1070-6631. S2CID 118722952.
- ^ Frenkel, E.; Losev, A.; Nekrasov, N. (2007). "Notes on instantons in topological field theory and beyond". Nuclear Physics B: Proceedings Supplements. 171: 215–230. arXiv:hep-th/0702137. Bibcode:2007NuPhS.171..215F. doi:10.1016/j.nuclphysbps.2007.06.013. S2CID 14914819.
- ^ Di Ventra, M.; Traversa, F. L.; Ovchinnikov, I. V. (2017). "Topological Field Theory and Computing with Instantons". Annalen der Physik. 2017 (12): 1700123. arXiv:1609.03230. Bibcode:2017AnP...52900123D. doi:10.1002/andp.201700123. ISSN 1521-3889. S2CID 9437990.















 t
t




















![{\displaystyle {\hat {H}}={\hat {L}}_{-\partial U}-\Theta {\hat {\triangle }}=[{\hat {d}},{\hat {\bar {d}}}],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0301a2f075d1b8040d0adea835857ba0ed3c4d49)








 (는)
(는) 



![{\textstyle {\hat {H}}={\hat {L}}_{-\partial U}+\Theta [{\hat {d}},{\hat {d}}^{\dagger }]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3840f330f9840514a333f7c9d8dd71127d340286)

 (가) 메트릭으로서
(가) 메트릭으로서![{\textstyle [{\hat {d}},{\hat {d}}^{\dagger }]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb2fc7ca4f91ae4dd8a5b639c855257d4d17ed0c)


![{\displaystyle {\hat {H}}_{U}=\Theta [{\hat {d}}_{U},{\hat {d}}_{U}^{\dagger }]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f72405be43773355d43dd04d0714f6d1d399860)





 스펙트럼이 실제적이고 음이 아님을 보여준다. 랜지빈 SDE의 SEO에게도 마찬가지다. 그러나 임의 형태의 SDE의 경우, 이는 더 이상 사실이 아니며, 이는 실제로 TS가 자연적으로 파괴될 수 있도록 하는 SEO의 고유값이 음수일 수도 있고 심지어 복잡할 수도 있기 때문이다.
스펙트럼이 실제적이고 음이 아님을 보여준다. 랜지빈 SDE의 SEO에게도 마찬가지다. 그러나 임의 형태의 SDE의 경우, 이는 더 이상 사실이 아니며, 이는 실제로 TS가 자연적으로 파괴될 수 있도록 하는 SEO의 고유값이 음수일 수도 있고 심지어 복잡할 수도 있기 때문이다. 














![{\displaystyle {\hat {H}}_{\alpha }={\hat {L}}_{F}-\Theta {\hat {L}}_{e_{a}}{\hat {L}}_{e_{a}}=[{\hat {d}},{\hat {\bar {d}}}_{\alpha }],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d0b53e7135b845194e0569f6b6b33d2a0b9d30d)


























 차이점이라고 하는 또 다른 방법일 뿐이다.
차이점이라고 하는 또 다른 방법일 뿐이다. 






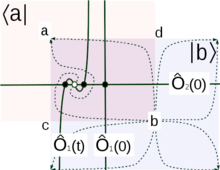










 (는) 하이젠베르크 표현에서 관측 가능한 것으로 t 0
(는) 하이젠베르크 표현에서 관측 가능한 것으로 t 0








