큐잉 이론

큐 네트워크는 단일 큐가 라우팅 네트워크에 의해 연결된 시스템입니다.이 이미지에서는 서버는 원으로, 큐는 직사각형으로, 라우팅 네트워크는 화살표로 표시됩니다.큐 네트워크의 연구에서는 일반적으로 네트워크의 평형 분포를 얻으려고 노력하지만, 많은 애플리케이션에서 과도 상태의 연구는 기초적입니다.

대기행렬 이론은 대기행렬 또는 ^[1]대기행렬에 대한 수학적인 연구이다.큐잉 모델은 큐의 길이와 대기시간을 ^[1]예측할 수 있도록 구성된다.큐잉 이론은 서비스 제공에 필요한 자원에 대한 비즈니스 결정을 내릴 때 자주 사용되기 때문에 일반적으로 운영 연구의 한 분야로 간주됩니다.

큐잉 이론은 애그너 크라루프 에를랑이 덴마크 ^[1]회사인 코펜하겐 전화 교환 회사의 시스템을 설명하는 모델을 만들었을 때 기원을 두고 있다.이 아이디어는 이후 통신, 교통 엔지니어링, 컴퓨팅^[2], 특히 산업 엔지니어링, 공장, 상점, 사무실 및 병원 설계, 프로젝트 ^[3]^[4]관리 등에서 응용되고 있습니다.

철자

큐잉보다 큐잉이라는 철자는 일반적으로 학술 연구 분야에서 볼 수 있습니다.실제로 이 분야의 대표 저널 중 하나는 큐잉 시스템즈입니다.

단일 큐잉 노드

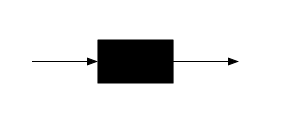
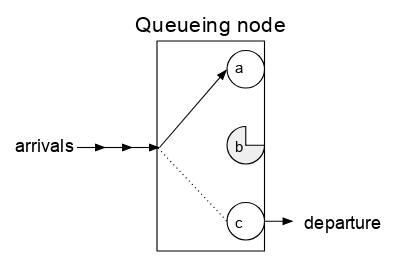
큐 또는 큐잉노드는 거의 블랙박스로 간주할 수 있습니다.작업 또는 "고객"이 큐에 도착합니다.잠시 대기하고 처리 시간이 걸린 후 큐에서 출발할 수 있습니다.

블랙박스.작업은 큐에 도착하거나 큐에서 출발합니다.

단, 큐잉노드는 큐잉노드 내부에 대한 정보가 필요하기 때문에 완전 블랙박스는 아닙니다.큐에는 1개 이상의 "서버"가 있으며, 각 서버는 출발할 때까지 도착 작업과 페어링할 수 있으며, 그 후 해당 서버는 다른 도착 작업과 페어링할 수 있습니다.

서버가 3개인 큐잉노드서버 a는 아이돌 상태이기 때문에 처리를 위해 서버 a에 착신이 주어집니다.서버 b는 현재 사용 중이므로 작업 서비스를 완료할 때까지 시간이 걸립니다.서버 c는 작업 서비스를 완료했기 때문에 도착 작업을 받을 수 있는 옆에 있습니다.

자주 사용되는 비유는 슈퍼마켓의 계산원 비유이다.다른 모델도 있지만, 이것은 문헌에서 흔히 볼 수 있는 모델이다.손님은 도착해서 계산원의 수속을 받고 출발한다.각 출납원은 한 번에 1명의 고객을 처리하므로 서버가 1대뿐인 큐잉 노드입니다.고객이 도착했을 때 계산원이 바쁠 경우 고객이 즉시 퇴장하는 설정을 버퍼가 없는 대기열(또는 "대기 영역" 또는 유사한 용어)이라고 합니다.최대 n개의 고객 대기존이 있는 설정은 버퍼가n인 큐라고 불립니다.

출생-사망 과정

단일 대기열('큐잉 노드'라고도 함)의 동작은 현재 시스템에 있는 작업 수('고객' 또는 '요청'이라고도 함)와 함께 대기열로부터의 도착 및 출발을 설명하는 출생-사망 프로세스에 의해 설명될 수 있습니다.도착은 작업 수를 1개 증가시키고 출발(서비스를 종료하는 작업)은 k를 1개 감소시킨다.

탄생-죽음의 과정이지원 안의 값은 출생-사망 과정의 상태를 나타냅니다.큐잉 시스템의 경우 k는 시스템 내 작업 수(대기 중인 작업 버퍼가 큐에 있는 경우 서비스 중이거나 대기 중)입니다.시스템은 각각 다양한 값 θ와_i_i μ에 의해 주어진 비율로 발생하는 k 값과 "births" 및 "deaths" 값 사이를 전환합니다.또한 큐의 경우 일반적으로 큐 내의 작업 수에 따라 도착률 및 출발률이 달라지지 않는 것으로 간주되므로 큐에 대한 단위시간당 도착/출발률의 단일 평균이 가정된다.이 가정 하에서 이 프로세스는 μ = μ₁, μ₂, μ, μ_k, ..., μ의_k 도달 속도₁₂ 및 μ = μ, μ, ..., μ의 이탈 속도를 가진다(다음 그림 참조).

서버 1대, 착신 레이트θ 및 출발 레이트μ를 가진 큐.

균형 방정식

생사 과정의 정상 상태 방정식은 균형 방정식으로 알려져 있으며, 다음과 같습니다. $P_{n}$ 서 $(\$ 은 $P_{n}$ 상태 n에 있을 정상 상태의 확률을 나타냅니다.

\displaystyle \mu _{1}P_{1}=\lambda _{0}P_{0}

\displayda _{0}P_{0}+\mu _{2}=(\lambda _{1}+\mu _{1})P_{1}

(\displaystyle \displaystyle _{n-1}P_{n-1}+\mu _{n}=(\lambda _{n}+\mu _{n})P_{n}}

처음 두 방정식은 다음을 의미한다.

P_{1}=black {\mu _{1}}P_{0

그리고.

{\displaystyle P_{2}=paramfrac {\mu _{2}}{\frac {1}+{\mu _{2}}({1}-\lambda _{0})=parc _{{0}{{{}}{{{})_p}_frac {{1}+{{{{{}}}}{{{{}}}}}}{{{}}}}}}}{{{{\frambda_f}}}}}}}}}}}}}}{{{{{{

수학적 귀납법에 의해

P_{n}=parcfrac {n-1}\cdots \cdots \cdots \{0}{n}{\mu _{n1}\cdots \mu _{0}=P_{0}\prod _{i=1}{nfrcda}{nfr}{nfr}

조건 $\sum _{n=0}^{\infty }P_{n}=P_{0}+P_{0}\sum _{n=1}^{\infty }\prod _{i=0}^{n-1}{\frac {\lambda _{i}}{\mu _{i+1}}}=1$ n $=$ 0 $\sum _{n=0}^{\infty }P_{n}=P_{0}+P_{0}\sum _{n=1}^{\infty }\prod _{i=0}^{n-1}{\frac {\lambda _{i}}{\mu _{i+1}}}=1$ P $\sum _{n=0}^{\infty }P_{n}=P_{0}+P_{0}\sum _{n=1}^{\infty }\prod _{i=0}^{n-1}{\frac {\lambda _{i}}{\mu _{i+1}}}=1$ $\sum _{n=0}^{\infty }P_{n}=P_{0}+P_{0}\sum _{n=1}^{\infty }\prod _{i=0}^{n-1}{\frac {\lambda _{i}}{\mu _{i+1}}}=1$ $\sum _{n=0}^{\infty }P_{n}=P_{0}+P_{0}\sum _{n=1}^{\infty }\prod _{i=0}^{n-1}{\frac {\lambda _{i}}{\mu _{i+1}}}=1$ + $\sum _{n=0}^{\infty }P_{n}=P_{0}+P_{0}\sum _{n=1}^{\infty }\prod _{i=0}^{n-1}{\frac {\lambda _{i}}{\mu _{i+1}}}=1$ 0 $\sum _{n=0}^{\infty }P_{n}=P_{0}+P_{0}\sum _{n=1}^{\infty }\prod _{i=0}^{n-1}{\frac {\lambda _{i}}{\mu _{i+1}}}=1$ $\sum _{n=0}^{\infty }P_{n}=P_{0}+P_{0}\sum _{n=1}^{\infty }\prod _{i=0}^{n-1}{\frac {\lambda _{i}}{\mu _{i+1}}}=1$ $\sum _{n=0}^{\infty }P_{n}=P_{0}+P_{0}\sum _{n=1}^{\infty }\prod _{i=0}^{n-1}{\frac {\lambda _{i}}{\mu _{i+1}}}=1$ 1 $\sum _{n=0}^{\infty }P_{n}=P_{0}+P_{0}\sum _{n=1}^{\infty }\prod _{i=0}^{n-1}{\frac {\lambda _{i}}{\mu _{i+1}}}=1$ $\sum _{n=0}^{\infty }P_{n}=P_{0}+P_{0}\sum _{n=1}^{\infty }\prod _{i=0}^{n-1}{\frac {\lambda _{i}}{\mu _{i+1}}}=1$ $\sum _{n=0}^{\infty }P_{n}=P_{0}+P_{0}\sum _{n=1}^{\infty }\prod _{i=0}^{n-1}{\frac {\lambda _{i}}{\mu _{i+1}}}=1$ $\sum _{n=0}^{\infty }P_{n}=P_{0}+P_{0}\sum _{n=1}^{\infty }\prod _{i=0}^{n-1}{\frac {\lambda _{i}}{\mu _{i+1}}}=1$ - 1 $\sum _{n=0}^{\infty }P_{n}=P_{0}+P_{0}\sum _{n=1}^{\infty }\prod _{i=0}^{n-1}{\frac {\lambda _{i}}{\mu _{i+1}}}=1$ i $\sum _{n=0}^{\infty }P_{n}=P_{0}+P_{0}\sum _{n=1}^{\infty }\prod _{i=0}^{n-1}{\frac {\lambda _{i}}{\mu _{i+1}}}=1$ i + $\sum _{n=0}^{\infty }P_{n}=P_{0}+P_{0}\sum _{n=1}^{\infty }\prod _{i=0}^{n-1}{\frac {\lambda _{i}}{\mu _{i+1}}}=1$ $=$ 1 （ \ $displaystyle$ \ $sum$ _ { n = $\sum _{n=0}^{\infty }P_{n}=P_{0}+P_{0}\sum _{n=1}^{\infty }\prod _{i=0}^{n-1}{\frac {\lambda _{i}}{\mu _{i+1}}}=1$ 0 }^{\infty $} P_{$ n} = $P_{0$ + $P_0$ } \ $sum$ = 1 ^{ n } ^{ n } ^{ n } } ^{ n } ^{ n ^{ n } ^{ n } } ^{ n }

P_{0}={1+\sum_{n=1}^{\infty}\display_{i=0}^{n-1}{\frac {\mu _{i+1}}}}

이는 $(\$ $n$ 1)의 방정식과 함께 필요한 정상 상태 확률을 완전히 설명합니다.

켄달 표기법

단일 큐잉 노드는 보통 Kendall 표기법을 사용하여 A/S/c 형식으로 기술됩니다.여기서 A는 큐에 도착하는 각 시간 간의 분포, S는 작업의 서비스 시간 분포, c는 ^[5]^[6]노드의 서버 수를 나타냅니다.표기의 예로서 M/M/1 큐는 단일 서버가 포아송 프로세스에 따라 도달하고(도착간 지속시간이 기하급수적으로 분포하는) 서비스 시간을 갖는 작업을 처리하는 단순한 모델이다(M은 마르코프 프로세스를 나타낸다).M/G/1 큐에서 G는 "general"을 나타내며 서비스 시간에 대한 임의의 확률 분포를 나타냅니다.

M/M/1 큐 분석 예시

1개의 서버를 가진 큐와 다음 특성을 고려합니다.

②: 도착률(예: 초당 10명의 고객)
μ: 평균 서비스 시간의 역수(같은 단위 시간당 예상되는 연속 서비스 완료 횟수, 예를 들어 30초당)
n: 시스템 내 고객 수를 나타내는 파라미터
P_n: 시스템 내에 안정된 상태의 고객이 n명 있을 가능성.

또, E는 시스템이 상태 n이 되는 회수를 나타내고_n, L은 시스템이 상태 n이 되는 회수를 나타낸다_n.모든 n에 대해_n E - L_n { {0, 1).즉, 시스템이 상태를 이탈하는 횟수는 시스템이 상태가 되는 횟수와 최대 1회 차이가 납니다. 이는 시스템이 나중에 해당 상태로 돌아가거나(E_n_n = L_n) 그렇지 않을 수 있기 때문입니다(E_n - L = 1).

시스템이 정상 상태에 도달하면 도착 속도는 출발 속도와 같아야 합니다.

따라서 균형 방정식은

\displaystyle \mu P_{1}=\lambda P_{0}

\displaystyle \da P_{0}+\mu P_{2}=(\lambda +\mu )P_{1}}

\displaystyle \lambda P_{n-1}+\mu P_{n+1}=(\lambda +\mu)P_{n}}

암시하다

P_{n}=frac {\mu }}P_{n-1},\n=1,2,\ldots

$P_{0}+P_{1}+\cdots =1$ 0 $P_{0}+P_{1}+\cdots =1$ + $P_{0}+P_{1}+\cdots =1$ 1 + $P_{0}+P_{1}+\cdots =1$ θ $P_{0}+P_{1}+\cdots =1$ { $displaystyle P_{0}$ + $P_{1$ } + \ $cdots = 1$ $P_{0}+P_{1}+\cdots =1$ 기하학적 분포식이 된다.

P_{n}=(1-\rho)\rho ^{n

$여기$ 서 $\rho ={\frac {\lambda }{\mu }}<1.$ $\rho ={\frac {\lambda }{\mu }}<1.$ < 1. $\rho ={\frac {\lambda }{\mu }}<1.$ {\ $displaystyle$ \ $rho = fr$ frac ${\mu }}$ < $\rho ={\frac {\lambda }{\mu }}<1.$ 1 . $}$

심플한 2등

일반적인 기본 큐잉 시스템은 Erlang에 기인하며 Little's Law의 수정한 것입니다.착신 레이트 θ, 드롭아웃 레이트 θ 및 이탈 레이트 μ에 따라 큐 L의 길이는 다음과 같이 정의된다.

L=frac}{\mu}.

요율의 지수 분포를 가정할 때, 대기 시간 W는 제공되는 도착의 비율로 정의할 수 있다.이는 대기 기간 동안 탈락하지 않은 사람들의 지수 생존율과 동일하며, 다음과 같은 결과를 얻을 수 있습니다.

(\displaystyle\frac{\mu}}=e^{-W{\mu}})

두 번째 방정식은 일반적으로 다음과 같이 고쳐 씁니다.

W=mathfrac {1}{\mu}}\mathrm {ln}{frac {\mu }

2단계 원박스 모델은 역학에서 ^[7]일반적이다.

이론 개발의 개요

1909년 코펜하겐 전화 교환소에서 일했던 덴마크 엔지니어 Agner Krarup Erlang은 현재 큐잉 ^[8]^[9]^[10]이론이라고 불리는 것에 대한 첫 번째 논문을 발표했다.그는 포아송 프로세스에 의해 교환기에 도착하는 전화의 수를 모델링하고 1917년 M/D/1 큐, 1920년 ^[11]M/D/k 큐잉 모델을 해결했습니다.Kendall 표기법:

M은 마르코프(Markov) 또는 무기억(memoryless)을 의미하며 포아송 프로세스에 따라 도착이 발생한다는 의미이다.
D는 결정론적(deterministic)을 의미하며 일정한 양의 서비스를 필요로 하는 큐에 도착하는 작업을 의미합니다.
k는 큐잉노드의 서버 수를 나타냅니다(k = 1, 2, ...).

노드의 작업이 서버 수보다 많을 경우 작업은 큐잉되어 서비스를 대기합니다.

M/G/1 큐는 1930년 ^[12]펠릭스 폴라체크에 의해 해결되었으며, 이후 알렉산드르 킨친에 의해 확률론적 용어로 재구성되어 현재는 폴라체크-킨친 ^[11]^[13]공식으로 알려져 있다.

1940년대 이후 큐잉 이론은 ^[13]수학자들에게 흥미로운 연구 분야가 되었다.1953년 David George Kendall은 GI/M/k^[14] 큐를 풀고 현재 Kendall의 표기법으로 알려진 큐의 현대적인 표기법을 도입했습니다.1957년에 Pollaczek은 적분 ^[15]방정식을 사용하여 GI/G/1을 연구했다.존 킹맨은 G/G/1 큐의 평균 대기 시간에 대한 공식인 킹맨의 [16]공식을 제공했습니다.

Leonard Kleinrock은 1960년대 초의 메시지 교환과 1970년대 초의 패킷 교환에 대한 큐잉 이론의 적용을 연구했습니다.1962년 매사추세츠공과대학 박사학위 논문으로 1964년 책으로 출간됐다.1970년대 초에 발표된 그의 이론적 연구는 인터넷의 선구자인 ARPANET에서 패킷 교환의 사용을 뒷받침했다.

매트릭스 기하학적 방법 및 매트릭스 해석 방법에서는 위상형 도착간 분포 및 서비스 시간 분포를 가진 큐를 ^[17]고려할 수 있습니다.

결합된 궤도를 가진 시스템은 무선 네트워크와 신호 처리에 대한 적용에서 큐잉 이론에서 중요한 부분입니다.^[18]

M/G/k 큐의 퍼포먼스메트릭 등의 문제는 해결되지 않은 ^[11]^[13]채로 있습니다.

서비스 분야

First In First Out(FIFO; 퍼스트 인 퍼스트 아웃) 큐의 예.

큐잉 노드에서는 다양한 스케줄링 정책을 사용할 수 있습니다.

선입선출: 선착순(FCFS)^[19]이라고도 불리는 이 원칙은 고객이 한 번에 하나씩 서비스를 받고 가장 오래 기다린 고객이 ^[20]먼저 서비스를 받는다는 것입니다.

라스트 인 퍼스트 아웃: 이 원칙은 한 번에 1명씩 고객에게 서비스를 제공하지만, 대기 시간이 가장 짧은 고객이 ^[20]먼저 서비스를 제공합니다.스택이라고도 합니다.

프로세서 공유: 서비스 용량은 고객 ^[20]간에 균등하게 분배됩니다.

우선 순위.: 우선 순위가 높은 고객이 ^[20]먼저 서비스를 받습니다.priority 큐에는 비선제형(서비스 중인 작업을 중단할 수 없음)과 프리엠프티브형(서비스 중인 작업이 더 높은 priority 작업에 의해 중단될 수 있음)의 두 가지 유형이 있습니다.어느 ^[21]모델에서도 작업이 손실되지 않습니다.

최단시간 작업 우선: 다음에 할 일은 크기가 가장 작은^[22] 직종이다.

최단 프리엠프티브 작업 우선: 다음 근무는 원래 크기가 가장^[23] 작은 직종입니다.

최단 남은 처리 시간: 다음 서비스 작업은 남은 처리 ^[24]요건이 가장 적은 작업입니다.

서비스 시설

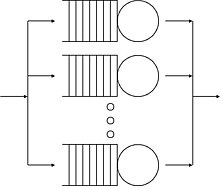
단일 서버: 고객이 줄을 서서 서버가 1대뿐
병렬 서버 여러 대– 단일 큐: 고객이 줄을 서서 여러 대의 서버가 있습니다.
여러 서버: 여러 개의 큐: 카운터가 있어 큐잉 장소를 고객이 결정할 수 있습니다.

신뢰할 수 없는 서버

서버 장애는 확률적 프로세스(일반적으로 Poisson)에 따라 발생하며 서버를 사용할 수 없는 설정 기간이 계속됩니다.중단된 고객은 서버가 ^[25]수리될 때까지 서비스 영역에 남아 있습니다.

고객의 대기행동작

망설임: 큐가 너무 길면 큐에 참여하지 않기로 결정한 고객
Jokeying: 고객이 큐를 전환함으로써 보다 신속하게 서비스를 받을 수 있다고 생각되는 경우 큐를 전환합니다.
리뉴얼: 고객이 서비스를 너무 오래 기다린 경우 큐에서 탈퇴합니다.

(큐에 버퍼가 없거나 고객의 방해 또는 위반으로 인해) 서비스가 제공되지 않는 도착 고객은 드롭아웃이라고도 하며, 평균 드롭아웃 속도는 큐를 나타내는 중요한 파라미터입니다.

네트워크 큐잉

큐 네트워크는 다수의 큐가 고객 라우팅이라고 불리는 것으로 연결되어 있는 시스템입니다.고객이 1개의 노드에서 서비스를 제공받으면 해당 노드는 다른 노드에 가입하여 서비스를 받기 위해 큐잉하거나 네트워크를 탈퇴할 수 있습니다.

m 노드의 네트워크의 경우 시스템 상태는 m차원 벡터(x₁, x₂, ..., x_m)로 설명할 수 있습니다.여기서_i x는 각 노드의 고객 수를 나타냅니다.

큐의 가장 단순한 단순하지 않은 네트워크는 ^[26]탠덤 큐라고 불립니다.이 영역에서 가장 중요한 첫 번째 결과는 효율적인 ^[27]^[28]제품 형태의 고정 분포가 존재하는 잭슨 네트워크와 throughput 및 체류 시간과 같은 평균 메트릭을 ^[30]계산할 수 있는 평균값^[29] 분석이었다.네트워크 내의 총 고객 수가 일정하게 유지되는 경우 네트워크를 폐쇄형 네트워크라고 하며 고든-뉴웰 ^[31]정리에서도 제품 형태의 고정 분포를 갖는 것으로 나타났습니다.이 결과는 BCMP^[32] 네트워크까지 확장되었습니다.여기서 서비스 시간, 시스템 및 고객 라우팅이 매우 일반적인 네트워크는 제품 형식의 고정 분포를 나타내고 있습니다.정규화 상수는 ^[33]1973년에 제안된 Buzen의 알고리즘으로 계산할 수 있다.

고객 네트워크도 조사되고 있습니다.Kelly 네트워크에서는 다양한 클래스의 고객이 다른 서비스 ^[34]노드에서 다른 우선순위 레벨을 경험하고 있습니다.또 다른 유형의 네트워크는 1993년 ^[35]Erol Gelenbe가 처음 제안한 G-networks입니다.이들 네트워크는 잭슨 네트워크와 같은 지수적인 시간 분포를 가정하지 않습니다.

라우팅 알고리즘

어떤 서비스 노드가 언제든지 활성화될 수 있는지에 제약이 있는 이산 시간 네트워크에서는 각 작업이 1인 서비스 ^[19]노드만 방문했을 때 최대 무게 스케줄링 알고리즘은 최적의 스루풋을 제공하는 서비스 정책을 선택합니다.서비스 정책을 선택합니다.작업이 여러 노드를 방문할 수 있는 보다 일반적인 경우, 백프레셔 라우팅은 최적의 throughput을 제공합니다.네트워크 스케줄러는 대규모^{[citation needed]} 네트워크의 특성에 영향을 주는 큐잉 알고리즘을 선택해야 합니다.큐잉 시스템의 스케줄링에 대한 자세한 내용은 확률적 스케줄링도 참조하십시오.

평균 필드 제한

평균장 모델에서는 큐의 수(m 위의)가 무한대에 도달함에 따라 경험적 측정(다른 상태에 있는 큐의 비율)의 제한 동작을 고려합니다.네트워크 내의 임의의 큐에 대한 다른 큐의 영향은 미분방정식에 의해 근사됩니다.결정론적 모형은 원래 ^[36]모형과 동일한 정적 분포로 수렴됩니다.

대량의 트래픽/확산 근사치

높은 점유율(이용률 1 근처)을 가진 시스템에서는 높은 트래픽 근사치를 사용하여 반사된 브라운 운동(^[37]Ornstein)에 의한 대기 시간 프로세스를 근사할 수 있다.Uhlenbeck 과정 또는 더 일반적인 확산 과정.^[38]브라운 프로세스의 차원 수는 큐잉 노드 수와 동일하며 확산은 음이 아닌 직교로 제한됩니다.

유체 한계

유체 모델은 프로세스가 시공간에서 스케일링될 때 한계치를 취하여 이기종 객체를 허용함으로써 얻을 수 있는 큐잉 네트워크의 연속적인 결정론적 아날로그입니다.이 축척된 궤적은 시스템의 안정성을 증명할 수 있는 결정론적 방정식으로 수렴됩니다.큐잉 네트워크는 안정적이지만 ^[39]유체 한계가 불안정한 것으로 알려져 있습니다.

「」를 참조해 주세요.

레퍼런스

^ ^a ^b ^c Sundarapandian, V. (2009). "7. Queueing Theory". Probability, Statistics and Queueing Theory. PHI Learning. ISBN 978-8120338449.
^ Lawrence W. Dowdy, Virgilio A.F. Almeida, Daniel A. Menasce. "Performance by Design: Computer Capacity Planning by Example". Archived from the original on 2016-05-06. Retrieved 2009-07-08.
^ Schlechter, Kira (March 2, 2009). "Hershey Medical Center to open redesigned emergency room". The Patriot-News. Archived from the original on June 29, 2016. Retrieved March 12, 2009.
^ Mayhew, Les; Smith, David (December 2006). Using queuing theory to analyse completion times in accident and emergency departments in the light of the Government 4-hour target. Cass Business School. ISBN 978-1-905752-06-5. Archived from the original on September 7, 2021. Retrieved 2008-05-20.
^ "Tijms, H.C, Algorithmic Analysis of Queues", 확률모델의 제9장, Wiley, Chickhester, 2003
^ Kendall, D. G. (1953). "Stochastic Processes Occurring in the Theory of Queues and their Analysis by the Method of the Imbedded Markov Chain". The Annals of Mathematical Statistics. 24 (3): 338–354. doi:10.1214/aoms/1177728975. JSTOR 2236285.
^ Hernández-Suarez, Carlos (2010). "An application of queuing theory to SIS and SEIS epidemic models". Math. Biosci. 7 (4): 809–823. doi:10.3934/mbe.2010.7.809. PMID 21077709.
^ "Agner Krarup Erlang (1878-1929) plus.maths.org". Pass.maths.org.uk. 1997-04-30. Archived from the original on 2008-10-07. Retrieved 2013-04-22.
^ Asmussen, S. R.; Boxma, O. J. (2009). "Editorial introduction". Queueing Systems. 63 (1–4): 1–2. doi:10.1007/s11134-009-9151-8. S2CID 45664707.
^ Erlang, Agner Krarup (1909). "The theory of probabilities and telephone conversations" (PDF). Nyt Tidsskrift for Matematik B. 20: 33–39. Archived from the original (PDF) on 2011-10-01.
^ ^a ^b ^c Kingman, J. F. C. (2009). "The first Erlang century—and the next". Queueing Systems. 63 (1–4): 3–4. doi:10.1007/s11134-009-9147-4. S2CID 38588726.
^ 폴라체크, F., Ueber eine Aufgabe der Wahrscheinlichkeitstherie, 수학 Z. 1930
^ ^a ^b ^c Whittle, P. (2002). "Applied Probability in Great Britain". Operations Research. 50 (1): 227–239. doi:10.1287/opre.50.1.227.17792. JSTOR 3088474.
^ 켄달, D.G:큐 이론에서 발생하는 확률적 과정과 임베디드 마르코프 체인 앤의 방법에 의한 분석.수학. 1953년 통계
^ Pollaczek, F., Problémes Prochoastiques posés par le pénoméne de formation d'une 큐
^ Kingman, J. F. C.; Atiyah (October 1961). "The single server queue in heavy traffic". Mathematical Proceedings of the Cambridge Philosophical Society. 57 (4): 902. Bibcode:1961PCPS...57..902K. doi:10.1017/S0305004100036094. JSTOR 2984229.
^ Ramaswami, V. (1988). "A stable recursion for the steady state vector in markov chains of m/g/1 type". Communications in Statistics. Stochastic Models. 4: 183–188. doi:10.1080/15326348808807077.
^ Morozov, E. (2017). "Stability analysis of a multiclass retrial system withcoupled orbit queues". Proceedings of 14th European Workshop. Lecture Notes in Computer Science. Vol. 17. pp. 85–98. doi:10.1007/978-3-319-66583-2_6. ISBN 978-3-319-66582-5.
^ ^a ^b Manuel, Laguna (2011). Business Process Modeling, Simulation and Design. Pearson Education India. p. 178. ISBN 9788131761359. Retrieved 6 October 2017.
^ ^a ^b ^c ^d Penttinen A., 제8장 – 큐잉 시스템, 강의 노트: S-38.145 - 텔레트라픽 이론 소개
^ Harchol-Balter, M. (2012). "Scheduling: Non-Preemptive, Size-Based Policies". Performance Modeling and Design of Computer Systems. pp. 499–507. doi:10.1017/CBO9781139226424.039. ISBN 9781139226424.
^ Andrew S. Tanenbaum; Herbert Bos (2015). Modern Operating Systems. Pearson. ISBN 978-0-13-359162-0.
^ Harchol-Balter, M. (2012). "Scheduling: Preemptive, Size-Based Policies". Performance Modeling and Design of Computer Systems. pp. 508–517. doi:10.1017/CBO9781139226424.040. ISBN 9781139226424.
^ Harchol-Balter, M. (2012). "Scheduling: SRPT and Fairness". Performance Modeling and Design of Computer Systems. pp. 518–530. doi:10.1017/CBO9781139226424.041. ISBN 9781139226424.
^ Dimitriou, I. (2019). "A Multiclass Retrial System With Coupled Orbits And Service Interruptions: Verification of Stability Conditions". Proceedings of FRUCT 24. 7: 75–82.
^ "Archived copy" (PDF). Archived (PDF) from the original on 2017-03-29. Retrieved 2018-08-02.{{cite web}}: CS1 maint: 제목으로 아카이브된 복사(링크)
^ Jackson, J. R. (1957). "Networks of Waiting Lines". Operations Research. 5 (4): 518–521. doi:10.1287/opre.5.4.518. JSTOR 167249.
^ Jackson, James R. (Oct 1963). "Jobshop-like Queueing Systems". Management Science. 10 (1): 131–142. doi:10.1287/mnsc.1040.0268. JSTOR 2627213.
^ Reiser, M.; Lavenberg, S. S. (1980). "Mean-Value Analysis of Closed Multichain Queuing Networks". Journal of the ACM. 27 (2): 313. doi:10.1145/322186.322195. S2CID 8694947.
^ Van Dijk, N. M. (1993). "On the arrival theorem for communication networks". Computer Networks and ISDN Systems. 25 (10): 1135–2013. doi:10.1016/0169-7552(93)90073-D. Archived from the original on 2019-09-24. Retrieved 2019-09-24.
^ Gordon, W. J.; Newell, G. F. (1967). "Closed Queuing Systems with Exponential Servers". Operations Research. 15 (2): 254. doi:10.1287/opre.15.2.254. JSTOR 168557.
^ Baskett, F.; Chandy, K. Mani; Muntz, R.R.; Palacios, F.G. (1975). "Open, closed and mixed networks of queues with different classes of customers". Journal of the ACM. 22 (2): 248–260. doi:10.1145/321879.321887. S2CID 15204199.
^ Buzen, J. P. (1973). "Computational algorithms for closed queueing networks with exponential servers" (PDF). Communications of the ACM. 16 (9): 527–531. doi:10.1145/362342.362345. S2CID 10702. Archived (PDF) from the original on 2016-05-13. Retrieved 2015-09-01.
^ Kelly, F. P. (1975). "Networks of Queues with Customers of Different Types". Journal of Applied Probability. 12 (3): 542–554. doi:10.2307/3212869. JSTOR 3212869.
^ Gelenbe, Erol (Sep 1993). "G-Networks with Triggered Customer Movement". Journal of Applied Probability. 30 (3): 742–748. doi:10.2307/3214781. JSTOR 3214781.
^ Bobbio, A.; Gribaudo, M.; Telek, M. S. (2008). "Analysis of Large Scale Interacting Systems by Mean Field Method". 2008 Fifth International Conference on Quantitative Evaluation of Systems. p. 215. doi:10.1109/QEST.2008.47. ISBN 978-0-7695-3360-5. S2CID 2714909.
^ Chen, H.; Whitt, W. (1993). "Diffusion approximations for open queueing networks with service interruptions". Queueing Systems. 13 (4): 335. doi:10.1007/BF01149260. S2CID 1180930.
^ Yamada, K. (1995). "Diffusion Approximation for Open State-Dependent Queueing Networks in the Heavy Traffic Situation". The Annals of Applied Probability. 5 (4): 958–982. doi:10.1214/aoap/1177004602. JSTOR 2245101.
^ Bramson, M. (1999). "A stable queueing network with unstable fluid model". The Annals of Applied Probability. 9 (3): 818–853. doi:10.1214/aoap/1029962815. JSTOR 2667284.

추가 정보

Gross, Donald; Carl M. Harris (1998). Fundamentals of Queueing Theory. Wiley. ISBN 978-0-471-32812-4. 온라인.
Zukerman, Moshe (2013). Introduction to Queueing Theory and Stochastic Teletraffic Models (PDF). arXiv:1307.2968.
Deitel, Harvey M. (1984) [1982]. An introduction to operating systems (revisited first ed.). Addison-Wesley. p. 673. ISBN 978-0-201-14502-1. 15장, 380–412페이지
Gelenbe, Erol; Isi Mitrani (2010). Analysis and Synthesis of Computer Systems. World Scientific 2nd Edition. ISBN 978-1-908978-42-4.
Newell, Gordron F. (1 June 1971). Applications of Queueing Theory. Chapman and Hall.
Leonard Kleinrock, Information Flow in Large Communication Nets, (MIT, Cambridge, 1961년 5월 31일) 박사학위 제안서.논문
레너드 클라인록입니다대규모 통신망에서의 정보 흐름(RLE 분기 진척 보고서, 1961년 7월)
레너드 클라인록입니다통신망: 확률적 메시지 흐름 및 지연 (McGrow-Hill, New York, 1964년)
Kleinrock, Leonard (2 January 1975). Queueing Systems: Volume I – Theory. New York: Wiley Interscience. pp. 417. ISBN 978-0471491101.
Kleinrock, Leonard (22 April 1976). Queueing Systems: Volume II – Computer Applications. New York: Wiley Interscience. pp. 576. ISBN 978-0471491118.
Lazowska, Edward D.; John Zahorjan; G. Scott Graham; Kenneth C. Sevcik (1984). Quantitative System Performance: Computer System Analysis Using Queueing Network Models. Prentice-Hall, Inc. ISBN 978-0-13-746975-8.
Jon Kleinberg; Éva Tardos (30 June 2013). Algorithm Design. Pearson. ISBN 978-1-292-02394-6.

외부 링크

큐잉 이론 계산기
Teknomo 큐잉 이론 튜토리얼 및 계산기
YouTube에서의 사무실 화재 긴급 대피 시뮬레이션
Virtamo 큐잉 이론 코스
Myron Hlynka의 큐잉 이론 페이지
큐잉 이론의 기초
일부 기존 큐잉 시스템을 해결하기 위한 무료 온라인 도구
JMT: 큐잉 이론을 위한 오픈 소스 그래픽 환경
LINE: 큐잉 모델을 해결하는 범용 엔진
줄을 서서 기다리는 것이 가장 싫은 점: (대기시간이 아닙니다.) By Seth Stevenson, Slate, 2012 – 인기 있는 소개

[sun-1] Sundarapandian, V. (2009). "7. Queueing Theory". Probability, Statistics and Queueing Theory. PHI Learning. ISBN 978-8120338449.

[2] Lawrence W. Dowdy, Virgilio A.F. Almeida, Daniel A. Menasce. "Performance by Design: Computer Capacity Planning by Example". Archived from the original on 2016-05-06. Retrieved 2009-07-08.

[3] Schlechter, Kira (March 2, 2009). "Hershey Medical Center to open redesigned emergency room". The Patriot-News. Archived from the original on June 29, 2016. Retrieved March 12, 2009.

[4] Mayhew, Les; Smith, David (December 2006). Using queuing theory to analyse completion times in accident and emergency departments in the light of the Government 4-hour target. Cass Business School. ISBN 978-1-905752-06-5. Archived from the original on September 7, 2021. Retrieved 2008-05-20.

[tijms-5] "Tijms, H.C, Algorithmic Analysis of Queues", 확률모델의 제9장, Wiley, Chickhester, 2003

[6] Kendall, D. G. (1953). "Stochastic Processes Occurring in the Theory of Queues and their Analysis by the Method of the Imbedded Markov Chain". The Annals of Mathematical Statistics. 24 (3): 338–354. doi:10.1214/aoms/1177728975. JSTOR 2236285.

[7] Hernández-Suarez, Carlos (2010). "An application of queuing theory to SIS and SEIS epidemic models". Math. Biosci. 7 (4): 809–823. doi:10.3934/mbe.2010.7.809. PMID 21077709.

[8] "Agner Krarup Erlang (1878-1929) plus.maths.org". Pass.maths.org.uk. 1997-04-30. Archived from the original on 2008-10-07. Retrieved 2013-04-22.

[9] Asmussen, S. R.; Boxma, O. J. (2009). "Editorial introduction". Queueing Systems. 63 (1–4): 1–2. doi:10.1007/s11134-009-9151-8. S2CID 45664707.

[10] Erlang, Agner Krarup (1909). "The theory of probabilities and telephone conversations" (PDF). Nyt Tidsskrift for Matematik B. 20: 33–39. Archived from the original (PDF) on 2011-10-01.

[century-11] Kingman, J. F. C. (2009). "The first Erlang century—and the next". Queueing Systems. 63 (1–4): 3–4. doi:10.1007/s11134-009-9147-4. S2CID 38588726.

[12] 폴라체크, F., Ueber eine Aufgabe der Wahrscheinlichkeitstherie, 수학 Z. 1930

[century1-13] Whittle, P. (2002). "Applied Probability in Great Britain". Operations Research. 50 (1): 227–239. doi:10.1287/opre.50.1.227.17792. JSTOR 3088474.

[14] 켄달, D.G:큐 이론에서 발생하는 확률적 과정과 임베디드 마르코프 체인 앤의 방법에 의한 분석.수학. 1953년 통계

[15] Pollaczek, F., Problémes Prochoastiques posés par le pénoméne de formation d'une 큐

[16] Kingman, J. F. C.; Atiyah (October 1961). "The single server queue in heavy traffic". Mathematical Proceedings of the Cambridge Philosophical Society. 57 (4): 902. Bibcode:1961PCPS...57..902K. doi:10.1017/S0305004100036094. JSTOR 2984229.

[17] Ramaswami, V. (1988). "A stable recursion for the steady state vector in markov chains of m/g/1 type". Communications in Statistics. Stochastic Models. 4: 183–188. doi:10.1080/15326348808807077.

[18] Morozov, E. (2017). "Stability analysis of a multiclass retrial system withcoupled orbit queues". Proceedings of 14th European Workshop. Lecture Notes in Computer Science. Vol. 17. pp. 85–98. doi:10.1007/978-3-319-66583-2_6. ISBN 978-3-319-66582-5.

[Manuel-19] Manuel, Laguna (2011). Business Process Modeling, Simulation and Design. Pearson Education India. p. 178. ISBN 9788131761359. Retrieved 6 October 2017.

[penttinen-20] Penttinen A., 제8장 – 큐잉 시스템, 강의 노트: S-38.145 - 텔레트라픽 이론 소개

[21] Harchol-Balter, M. (2012). "Scheduling: Non-Preemptive, Size-Based Policies". Performance Modeling and Design of Computer Systems. pp. 499–507. doi:10.1017/CBO9781139226424.039. ISBN 9781139226424.

[22] Andrew S. Tanenbaum; Herbert Bos (2015). Modern Operating Systems. Pearson. ISBN 978-0-13-359162-0.

[23] Harchol-Balter, M. (2012). "Scheduling: Preemptive, Size-Based Policies". Performance Modeling and Design of Computer Systems. pp. 508–517. doi:10.1017/CBO9781139226424.040. ISBN 9781139226424.

[24] Harchol-Balter, M. (2012). "Scheduling: SRPT and Fairness". Performance Modeling and Design of Computer Systems. pp. 518–530. doi:10.1017/CBO9781139226424.041. ISBN 9781139226424.

[25] Dimitriou, I. (2019). "A Multiclass Retrial System With Coupled Orbits And Service Interruptions: Verification of Stability Conditions". Proceedings of FRUCT 24. 7: 75–82.

[26] "Archived copy" (PDF). Archived (PDF) from the original on 2017-03-29. Retrieved 2018-08-02.{{cite web}}: CS1 maint: 제목으로 아카이브된 복사(링크)

[27] Jackson, J. R. (1957). "Networks of Waiting Lines". Operations Research. 5 (4): 518–521. doi:10.1287/opre.5.4.518. JSTOR 167249.

[jackson-28] Jackson, James R. (Oct 1963). "Jobshop-like Queueing Systems". Management Science. 10 (1): 131–142. doi:10.1287/mnsc.1040.0268. JSTOR 2627213.

[29] Reiser, M.; Lavenberg, S. S. (1980). "Mean-Value Analysis of Closed Multichain Queuing Networks". Journal of the ACM. 27 (2): 313. doi:10.1145/322186.322195. S2CID 8694947.

[30] Van Dijk, N. M. (1993). "On the arrival theorem for communication networks". Computer Networks and ISDN Systems. 25 (10): 1135–2013. doi:10.1016/0169-7552(93)90073-D. Archived from the original on 2019-09-24. Retrieved 2019-09-24.

[31] Gordon, W. J.; Newell, G. F. (1967). "Closed Queuing Systems with Exponential Servers". Operations Research. 15 (2): 254. doi:10.1287/opre.15.2.254. JSTOR 168557.

[32] Baskett, F.; Chandy, K. Mani; Muntz, R.R.; Palacios, F.G. (1975). "Open, closed and mixed networks of queues with different classes of customers". Journal of the ACM. 22 (2): 248–260. doi:10.1145/321879.321887. S2CID 15204199.

[buzen-1973-33] Buzen, J. P. (1973). "Computational algorithms for closed queueing networks with exponential servers" (PDF). Communications of the ACM. 16 (9): 527–531. doi:10.1145/362342.362345. S2CID 10702. Archived (PDF) from the original on 2016-05-13. Retrieved 2015-09-01.

[34] Kelly, F. P. (1975). "Networks of Queues with Customers of Different Types". Journal of Applied Probability. 12 (3): 542–554. doi:10.2307/3212869. JSTOR 3212869.

[35] Gelenbe, Erol (Sep 1993). "G-Networks with Triggered Customer Movement". Journal of Applied Probability. 30 (3): 742–748. doi:10.2307/3214781. JSTOR 3214781.

[36] Bobbio, A.; Gribaudo, M.; Telek, M. S. (2008). "Analysis of Large Scale Interacting Systems by Mean Field Method". 2008 Fifth International Conference on Quantitative Evaluation of Systems. p. 215. doi:10.1109/QEST.2008.47. ISBN 978-0-7695-3360-5. S2CID 2714909.

[37] Chen, H.; Whitt, W. (1993). "Diffusion approximations for open queueing networks with service interruptions". Queueing Systems. 13 (4): 335. doi:10.1007/BF01149260. S2CID 1180930.

[38] Yamada, K. (1995). "Diffusion Approximation for Open State-Dependent Queueing Networks in the Heavy Traffic Situation". The Annals of Applied Probability. 5 (4): 958–982. doi:10.1214/aoap/1177004602. JSTOR 2245101.

[39] Bramson, M. (1999). "A stable queueing network with unstable fluid model". The Annals of Applied Probability. 9 (3): 818–853. doi:10.1214/aoap/1029962815. JSTOR 2667284.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[30]

[29]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

v t 큐잉 이론
단일 큐잉 노드	D/M/1 큐 M/D/1 큐 M/D/C 큐 M/M/1 큐 버크의 정리 M/M/c 큐 M/M/오브로드 큐 M/G/1 큐 폴라체크-킨차인 공식 매트릭스 분석법 M/G/k 큐 G/M/1 큐 G/G/1 큐 킹맨 공식 린들리 방정식 포크 결합 큐 벌크 큐
도착 프로세스	포아송 점 과정 마르코프 도착 과정 합리적인 도착 과정
네트워크 큐잉	잭슨 네트워크 트래픽 방정식 고든-뉴엘 정리 평균값 분석 부젠 알고리즘 켈리 네트워크 G네트워크 BCMP 네트워크
서비스 정책	선입선출 라이프 프로세서 공유 라운드 로빈 최단 시간 작업 최단 남은 시간
주요 개념	연속 시간 마르코프 연쇄 켄달 표기법 리틀의 법칙 제품형태솔루션 균형 방정식 준가역성 흐름 등가 서버 방식 도착 정리 분해법 베네시법
한계 정리	유체 한계 평균장 이론 혼잡한 트래픽의 근사치 반사 브라운 운동
내선번호	유체 큐 레이어드 큐잉 네트워크 폴링 시스템 적대 큐잉 네트워크 손실 네트워크 재심 큐
정보 시스템	데이터 버퍼 Erlang(유닛) 얼랑 분포 흐름 제어(데이터) 메시지 큐 네트워크 폭주 네트워크 스케줄러 파이프라인(소프트웨어) 서비스 품질 스케줄링(컴퓨팅) 텔레트래픽 공학
카테고리

권한 관리
국립도서관	프랑스. (데이터) 독일. 이스라엘 미국 일본. 체코 공화국
다른.	대상 용어의 적용 면

Search

큐잉 이론

네임스페이스

더

목차

철자

단일 큐잉 노드

출생-사망 과정

균형 방정식

켄달 표기법

M/M/1 큐 분석 예시

심플한 2등

이론 개발의 개요

서비스 분야

네트워크 큐잉

라우팅 알고리즘

평균 필드 제한

대량의 트래픽/확산 근사치

유체 한계

「」를 참조해 주세요.

레퍼런스

추가 정보

외부 링크

Search

큐잉 이론

철자

단일 큐잉 노드

출생-사망 과정

균형 방정식

켄달 표기법

M/M/1 큐 분석 예시

심플한 2등

이론 개발의 개요

서비스 분야

네트워크 큐잉

라우팅 알고리즘

평균 필드 제한

대량의 트래픽/확산 근사치

유체 한계

「 」를 참조해 주세요.

레퍼런스

추가 정보

외부 링크

「」를 참조해 주세요.