용해성
Solubility화학에서 용해성은 용질인 물질이 용매라는 다른 물질과 용액을 형성할 수 있는 능력이다.불용성(bonsubility)은 용질이 그러한 용액을 형성할 수 없는 정반대의 특성입니다.
특정 용매에서 물질의 용해성의 범위는 일반적으로 더 이상 [1]용해될 수 없는 포화 용액 중의 용질 농도로 측정된다.이 때 두 물질은 용해성 평형 상태에 있다고 한다.일부 용질 및 용제의 경우 이러한 한계가 없을 수 있으며, 이 경우 두 물질은 "모든 비율로 혼합 가능"(또는 "혼합 가능")[2]하다고 합니다.
용질은 고체, 액체 또는 기체가 될 수 있는 반면 용매는 보통 고체 또는 액체입니다.둘 다 순수한 물질일 수도 있고 그 자체가 해결책일 수도 있습니다.가스는 매우 극단적인 [3]상황을 제외하고 항상 모든 비율로 혼합될 수 있으며, 고체나 액체는 먼저 기체 상태로 통과해야만 기체 내에서 "분해"될 수 있습니다.
용해도는 온도와 압력뿐만 아니라 용질 및 용매의 성분(pH와 다른 용해 물질의 존재 포함)에 의해 주로 좌우됩니다.의존성은 종종 두 물질의 입자(atom, 분자 또는 이온) 사이의 상호작용과 엔탈피와 엔트로피와 같은 열역학 개념으로 설명될 수 있습니다.
특정 조건 하에서 용질의 농도는 통상적인 용해도 한계를 초과할 수 있다.그 결과 과포화 용액은 준전이 가능하며 적절한 핵생성 부위가 [4]나타나면 과잉 용질을 신속하게 배제합니다.
용해성의 개념은 수산화칼슘과 염산의 반응과 같이 두 물질 사이에 돌이킬 수 없는 화학 반응이 있을 때 적용되지 않는다. 비록 비공식적으로 한 물질이 다른 물질에 "분해"되었다고 말할 수 있다.용해도 역시 용액 속도와 같지 않습니다. 즉, 고체 용질이 액체 용매에 얼마나 빨리 용해되는지를 나타냅니다.이 특성은 두 물질의 물리적 형태, 혼합 방식 및 강도 등 다른 많은 변수에 따라 달라집니다.
용해성의 개념과 측정은 공학, 의학, 농업 그리고 심지어 그림, 청소, 요리, 양조 같은 비기술적인 활동뿐만 아니라 화학, 생물학, 물리학, 해양학 같은 많은 과학에서 매우 중요하다.과학적, 산업적 또는 실제적 관심이 있는 대부분의 화학 반응은 시약이 적절한 용매에 용해된 후에만 발생합니다.물은 단연코 그러한 용매 중 가장 흔한 것이다.
"[5]용해성"이라는 용어는 액체에서 매우 미세한 고체 입자의 콜로이드 현탁액을 형성할 수 있는 물질에 사용되기도 한다.그러나 이러한 물질의 정량적 용해성은 일반적으로 명확하게 정의되지 않는다.
용해도 정량화
특정 용매에서 특정 용질의 용해성은 일반적으로 두 [1]용매의 포화 용액의 농도로 표현된다.용매 또는 용액의 특정 질량, 부피 또는 몰 양에 대한 용질의 질량, 부피 또는 몰 양 등 용액의 농도를 표현하는 여러 가지 방법 중 하나를 사용할 수 있다.
용제량당
특히, 화학 핸드북은 종종 액체 속 물질의 용해도를 용매(g/dL) 데시리터당 용질(100mL) 그램으로 표현하거나, 덜 일반적으로는 리터당 그램(g/L)으로 표현한다.용제의 양은 g/100g" 또는 g/kg과 같이 질량으로 표시할 수 있다.이 경우 수치는 백분율로 표기할 수 있으며, "w/w"는 "weight per weight"[6]로 표기할 수 있다(g/L, g/kg의 값은 물의 경우 거의 동일하지만 다른 용제의 경우 동일하지 않다.
또는 용질량을 질량 대신 몰 단위로 표시할 수 있으며, 용매량을 킬로그램 단위로 지정하면 그 값은 용액의 몰리티(mol/kg)가 된다.
솔루션 수량당
액체 중의 물질의 용해성은 용제가 아니라 용액의 양당 용질량으로 표현될 수도 있다.예를 들어, 적정의 일반적인 관행에 따라 용액(mol/L)의 리터당 용질 몰(mol/L)로 표현될 수 있으며, 용질 몰(mol/L)은 용질 몰(mol/L))이다.
좀 더 특수한 맥락에서 용해도는 몰 분율(용질+용매의 총 몰당 용질 몰) 또는 평형 상태의 질량 분율(용질+용매 질량당 용질 질량)로 제공되며, 둘 다 백분율로 표현될 수 있다.
액체 및 기체 용질
액체에 포함된 액체 또는 기체의 용액의 경우, 두 물질의 양은 질량 또는 몰 양이 아닌 부피로 지정될 수 있습니다(예: 용매 리터당 용질량 또는 용액 리터당 용질량).이 값은 백분율로 지정할 수 있으며, "볼륨 당 볼륨"의 약어 "v/v"를 사용하여 이 선택을 나타낼 수 있습니다.
용해도 값 변환
용해도를 측정하는 이러한 다양한 방법 간의 변환은 종종 측정되지 않고 예측할 수 없는 솔루션의 밀도를 알아야 하기 때문에 사소한 것이 아닐 수 있습니다.총 질량은 용해로 보존되지만 최종 부피는 용제의 부피와 두 [7]부피의 합과는 다를 수 있다.
또한, 많은 고체(산 및 소금 등)는 용해될 때 비사소한 방식으로 분해됩니다. 반대로 용매는 용질의 분자 또는 이온과 배위 복합체를 형성할 수 있습니다.이 경우 용질과 용매 분자의 몰 합계는 실제로는 독립 입자 용액의 총 몰 합계가 아닙니다.이 문제를 피하기 위해 용질이 분리되거나 복합체를 형성하지 않는 것처럼, 즉 용액의 몰 양이 두 물질의 몰 양의 합이라고 가정하여 용액의 몰 당 용해도를 계산하고 인용한다.
용해도 정도를 설명하는 데 사용되는 수식어
용해성의 범위는 물에 있는 에탄올과 같은 무한 용해성(한계 없음, 즉 혼합성[2])에서 물에 있는 이산화티타늄과 같은 본질적으로 불용성까지 다양하다.주어진 어플리케이션에 대한 용해성의 정도를 규정하기 위해 많은 다른 설명적인 용어들도 사용된다.예를 들어, 미국 약국은 [8]용질량 m의su 단위 용해 시 필요한 용매sv m의 질량에 따라 다음과 같은 용어를 제공한다. (예시의 용해도는 20-25°C의 물에 대한 대략적인 값이다.)
| 용어 | 범위 | 예 | g/dL | msv/msu |
|---|---|---|---|---|
| 매우 용해성 | 1 미만 | 질산칼슘 | 158.7 | 0.63 |
| 용해성이 좋다 | 1~10 | 염화칼슘 | 65 | 1.54 |
| 용해성 | 10 ~ 30 | 옥살산나트륨 | 3.9 | 26 |
| 극소용해성 | 30 ~ 100 | |||
| 미용해성 | 100 ~ 1000 | 황산칼슘 | 0.21 | 490 |
| 매우 미미한 용해성 | 1000 ~ 10,000 | 인산 이칼슘 | 0.02 | 5000 |
| 사실상 불용성 또는 불용성 | ≥ 10,000 | 황산바륨 | 0.000245 | 409000 |
불용성 또는 유사한 용어로 기술하는 문턱값은 애플리케이션에 따라 다를 수 있습니다.예를 들어,[9] 용매 100 mL당 용해도가 0.1 g 미만인 물질을 "용해하지 않는" 물질로 기술한다.
분자뷰
용해도(solubility)는 동적 평형 하에서 발생하며, 이는 용해도(solubility)가 용해 및 위상 결합의 동시 및 반대 과정(예: 고형물의 침전)에서 발생한다는 것을 의미한다.용해성 평형은 두 프로세스가 동일한 속도로 진행되었을 때 발생합니다.
용해성이라는 용어는 용질이 용해에 의해 변화되는 일부 분야에서도 사용된다.예를 들어, 많은 금속과 그 산화물은 염산에 용해된다고 하지만, 실제로는 수산이 고체를 불가역적으로 분해하여 용해성 제품을 만든다.또한 대부분의 이온성 고형물은 극성 용제에 의해 용해되지만 이러한 과정은 가역적입니다.용제가 증발해도 용질이 회수되지 않는 경우에는 용해라고 한다.용해성의 열역학적 개념은 용해에는 직접적으로 적용되지 않는다.
용질이 녹으면 용액에 여러 종을 형성할 수 있다.예를 들어, 수산화철의 수성 현탁액인 Fe(
2OH)는 다음 계열을 포함할 것이다.[Fe(HO2)(xOH)]x(2x)+다른 종들도 있어요또한 수산화철의 용해성 및 그 가용성 성분의 조성은 pH에 따라 결정된다.일반적으로 용매상에서의 용해도는 열역학적으로 안정된 특정 용매에 대해서만 주어질 수 있으며, 용해도 값에는 용액 내의 모든 종(위의 예에서는 모든 철 함유 복합체)이 포함됩니다.
용해도에 영향을 미치는 요인
용해도는 특정 단계에 대해 정의됩니다.예를 들어 아라고나이트와 칼사이트는 탄산칼슘의 다형질이고 화학식이 동일하지만 물에 녹는 용해도에는 차이가 있을 것으로 예상된다.
다른 물질에서 한 물질의 용해성은 용매와 용질 사이의 분자간 힘의 균형과 용매화에 따른 엔트로피 변화에 의해 결정됩니다.온도와 압력 등의 요인에 의해 이 균형이 변화하여 용해도가 변화합니다.
용해성은 용매에 용해된 다른 종의 존재, 예를 들어 액체에서 복합형성 음이온(리간드)에 의해 크게 좌우될 수 있다.용해성은 또한 용액에 있는 공통 이온의 과잉 또는 결핍, 즉 공통 이온 효과로 알려진 현상에 의존합니다.용해성은 용액의 이온 강도에 따라 달라집니다.마지막 두 효과는 용해성 평형에 대한 방정식을 사용하여 정량화할 수 있다.
산화환원 반응으로 용해되는 고체의 경우 용해도는 전위에 따라 달라질 것으로 예상된다(고체가 열역학적으로 안정된 상태를 유지하는 전위 범위 내).예를 들어 산화성이 높은 FeO-FeO3423 레독스 버퍼를 사용하여 레독스 전위를 제어했을 때 고온수 중 금의 용해도는 중간산화 Ni-NiO [10]버퍼를 사용하는 경우보다 약 1배(약 10배) 높은 것으로 관찰된다.
용해도(포화에 가까운 농도로)는 결정 또는 용질 방울의 물리적 크기(또는 엄밀히 말하면 [11]용질의 특정 표면적 또는 몰 표면적)에 따라 달라진다.정량화는 용해도 평형에 관한 기사의 방정식을 참조한다.매우 결함이 있는 결정의 경우, 무질서의 정도가 증가함에 따라 용해도가 증가할 수 있습니다.이 두 효과 모두 결정의 깁스 에너지에 대한 용해도 상수의 의존성 때문에 발생합니다.마지막 두 가지 효과는 종종 측정하기 어렵지만 실질적으로 중요하다.[citation needed]예를 들어, 노화를 촉진하는 원동력이 된다(시간에 따라 자연스럽게 증가하는 결정 크기).
온도
주어진 용매에서 주어진 용질의 용해성은 온도의 함수이다.용해반응의 엔탈피(δH)의 변화, 즉 용해반응의 흡열성(δH > 0) 또는 발열성(δH < 0) 특성에 따라 특정 화합물의 용해도가 온도와 함께 증가하거나 감소하는 경우가 있다.van't Hoff 방정식은 용해도 평형상수(Ksp)의 변화와 온도 변화 및 반응 엔탈피 변화를 관련짓습니다.대부분의 고체 및 액체는 용해 반응이 흡열성이기 때문에 온도와 함께 용해도가 증가한다(δH > 0).[12]고온의 액체 물(예를 들어 임계 온도에 근접하는 것)에서는 액체 물의 특성 및 구조 변화에 따라 이온성 용매의 용해도가 감소하는 경향이 있다.유전율이 낮을수록 용매 극성이 낮아지고 용해 반응의 δG에 영향을 미치는 수화 에너지가 변화한다.
가스 용질은 온도에 따라 더 복잡한 동작을 보입니다.온도가 상승함에 따라 가스는 일반적으로 물에 덜 녹지만(수화와[13] 관련된 발열 용해 반응), 유기 용제(용매와 [12]관련된 발열 용해 반응)에는 더 잘 녹는다.
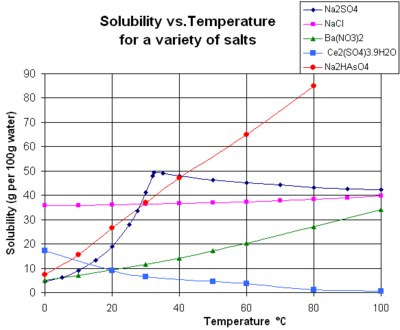
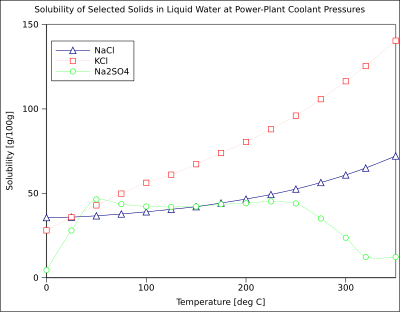
이 차트는 액체 상태의 물에 있는 일부 전형적인 고체 무기염에 대한 용해도 곡선을 보여준다(온도는 섭씨, 즉 켈빈 - 273.15).[14]많은 염은 질산바륨과 비산수소나트륨과 같은 작용을 하며, 온도에 따라 용해도가 크게 증가한다(δH > 0).일부 용질(예: 물 속의 염화나트륨)은 온도(δH 0 0)와 상당히 독립적인 용해성을 보인다.황산칼슘(석고) 및 황산세륨(II)과 같은 소수는 온도가 상승함에 따라 물에 덜 녹는다(δH < 0).[15]70°C에서 용해도가 25°C에서 값의 약 절반인 수산화칼슘(포르틀란다이트)도 마찬가지입니다.수산화칼슘이 물에 용해되는 것도 발열 과정(δH < 0)이며, van't Hoff 방정식과 Le Chatelier의 원리를 따른다.온도를 낮추면 용해열이 시스템에서 제거되므로 Ca(OH)2가 용해되기 쉬워집니다. 따라서 낮은 온도에서 포틀랜드산염 용해도가 증가합니다.이러한 온도 의존성을 "역행" 또는 "역행" 용해성이라고 부르기도 합니다.때로는 황산나트륨과 같이 보다 복잡한 패턴이 관찰되기도 하는데, 황산나트륨은 용해 반응에서 [citation needed]Gibs Free Energy(δG; 깁스 자유 에너지)의 변화가 적은 용해성 무수상(Thenardite)을 형성하기 위해 32°C에서 결정수를 잃는다.
유기화합물의 용해성은 거의 항상 온도에 따라 증가한다.고형물의 정화에 사용되는 재결정화 기술은 고온 용매와 저온 용매의 용매에 따라 달라집니다.특정 사이클로덱스트린과 [16]같은 몇 가지 예외가 있습니다.
압력.
응축상(용액 및 액체)의 경우 용해도의 압력 의존성은 일반적으로 약하며 실제로는 무시된다.이상적인 솔루션을 가정하면 의존성은 다음과 같이 수량화할 수 있습니다.
서 지수 i i는 구성 요소를 하고, })는 용액에서ii) 구성 요소의 몰 분율,(\ P는 압력, T T는 상온, q(.}}은 용액 성분의 몰 부피이며 { stylecr}는 용해 고체 중 성분의 몰 부피이며, styleR은 범용 가스 [17]상수이다
용해성의 압력 의존성은 때때로 실질적인 의미를 갖는다.예를 들어, 황산칼슘에 의한 유정 및 유정의 침전 오염(압력 저하로 용해도 저하)은 시간이 지남에 따라 생산성이 저하될 수 있습니다.
가스의 용해성
헨리의 법칙은 용제에 포함된 가스의 용해도를 정량화하기 위해 사용된다.용매에 포함된 가스의 용해도는 용매 위에 있는 가스의 부분 압력에 정비례합니다.이 관계는 라울트의 법칙과 비슷하며 다음과 같이 나타낼 수 있다.
H는 온도의존상수(예를 들어 298 K의 물에서 dioxygen(O2)의 경우 769.2 L·atm/mol),(\ p는 분압(ATM 내), c는 액체(in/L)에 용해된 가스의 농도이다.
가스의 용해도는 때때로 분젠 용해도 계수를 사용하여 정량화되기도 한다.
작은 기포가 존재하는 경우, 기체의 용해성은 압력에 대한 반지름의 영향을 통해서만 기포 반지름에 의존하지 않는다(즉, 작은 기포와 접촉하는 액체 내 가스의 용해성은 압력 증가에 의해 증가한다). 영-라플라스 [18]방정식 참조).
헨리의 법칙은 용해 시 화학적 사양의 변화를 겪지 않는 기체에 유효하다.시버트의 법칙은 이 가정이 성립되지 않는 경우를 보여준다.
바닷물의 이산화탄소 용해도는 온도, 용액의 pH 및 탄산염 완충제의 영향을 받는다.온도가 상승할 때 바닷물에서 이산화탄소의 용해도 감소는 남극 보스토크 현장의 얼음 코어에서 관측된 과거와 미래의 기후 변화를 악화시키는 중요한 역행 인자(긍정 피드백)이기도 하다.지질학적 시간 척도에서, 밀란코비치 주기 때문에, 지구 궤도와 그 회전축의 천문학적 매개변수가 점진적으로 변화하고 지구 표면에서 태양 복사 강도를 수정하면, 온도가 상승하기 시작합니다.탈글리세이션 기간이 시작되면, 해양의 점진적인 온난화는 따뜻한 바닷물에서 낮은 용해도로 인해 대기 중으로 이산화탄소를2 방출한다.반대로, 대기 중 CO의 수치가2 높을수록 온실 효과가 증가하고 이산화탄소는 일반적인 온난화의 증폭제 역할을 한다.
극성
용해도 예측에 사용되는 일반적인 격언은 라틴어로 "Similia similibus solventur"[19]로 표현되는 "like solves like"이다.이는 혼합의 바람직한 엔트로피를 바탕으로 자신과 유사한 화학구조를 가진 용매에서 용질이 가장 잘 녹는다는 것을 나타낸다.이 견해는 단순하지만 유용한 경험칙이다.용제의 전체적인 용매화 용량은 주로 [a]극성에 따라 달라집니다.예를 들어 요소와 같은 극성(친수성) 용질은 극성이 높은 물에 매우 잘 용해되고 극성이 높은 메탄올에는 덜 용해되며 벤젠과 같은 비극성 용매에는 실질적으로 용해되지 않습니다.반면 나프탈렌 등의 무극성 또는 친유성 용질은 물에 불용성이고 메탄올에 상당히 용해되며 무극성 [20]벤젠에 고용성이다.
보다 간단한 용어로 염화나트륨(일반 소금)과 같은 단순한 이온 화합물(양과 음이온 포함)은 물과 같은 극성 용매(공유 분자 내의 양()+)과 음()-) 전하 분리)에 쉽게 용해된다.따라서 바다는 초기 지질학 이후 용해된 소금을 축적하면서 짜다.나이 탓이다.
용해도는 혼합 엔트로피(δS)에 의해 선호되며 용해 엔탈피(δH)와 소수성 효과에 따라 달라진다.자유 용해 에너지(Gibbs 에너지)는 온도에 따라 달라지며 δG = δH – TδS의 관계에 따라 결정됩니다. δG가 작을수록 용해성이 높아집니다.
화학자들은 종종 액체-액체 추출 기술을 사용하여 반응 혼합물에서 화합물을 분리하고 정제하기 위해 용해성의 차이를 이용한다.이는 의약품 합성부터 사용후핵연료 재처리까지 화학의 광범위한 분야에 적용된다.
용해율
해산은 순간적인 과정이 아니다.용해율(kg/s)은 용해도 생성물 및 재료의 표면적과 관련이 있다.고체가 용해되는 속도는 비정질 고체와 표면적(결정질 크기) 및 다형성의 유무에 따라 결정성 또는 그 부족에 따라 달라질 수 있다.예를 들어 통제된 약물 전달 방법을 설계할 때 많은 실제 시스템이 이러한 효과를 설명한다.경우에 따라서는 용해성 평형을 확립하는 데 오랜 시간이 걸릴 수 있습니다(시간, 일, 월 또는 여러 해; 용질 및 기타 요소의 특성에 따라 다름).
용해 속도는 종종 Noyes로 나타낼 수 있다.휘트니 방정식 또는 네른스트 및 브루너[21] 방정식:
여기서:
- {\m} = 용해된 물질 질량
- t= 시간
- (\ A= 용해물질과 용제의 경계면 면적
- {\ D = 확산 계수
- \ d= 용해물질 표면의 용제 경계층 두께
- s\ = 표면의 물질 농도
- b { = 용매의 부피 중 물질 농도
확산에 의해 제한되는 용해(또는 혼합물이 존재하는 경우에는 질량 전달)의 경우, })는 물질의 용해도와 같다.순수물질의 용해율이 고체 표면적에 정규화되면(일반적으로 용해과정에서 시간에 따라 변화한다) kg/ms2 단위로 나타내며, 이를 "내용해율"이라고 한다.고유 용해율은 미국 약국에 의해 정의된다.
용해율은 시스템마다 크기 순서에 따라 달라집니다.일반적으로 매우 낮은 용해율은 낮은 용해도와 평행하며, 높은 용해율을 가진 물질은 Noyes-Whitney 방정식에서 제시된 바와 같이 높은 용해율을 보인다.
용해성 이론
용해도 산물
용해도 상수는 상대적으로 용해도가 낮은 이온 화합물의 포화 용액을 기술하는데 사용된다.용해도 상수는 평형 상수의 특수한 경우이다.평형 상태에서 이온 농도의 산물이므로 용해도 산물이라고도 한다.소금에서 나온 용해 이온과 용해되지 않은 소금 사이의 균형을 묘사합니다.용해도 상수는 또한 용해 반응의 반대인 침전에 "적용"할 수 있다(즉, 유용하다).다른 평형 상수와 마찬가지로 온도는 용해도 상수의 수치 값에 영향을 미칠 수 있습니다.용해도 상수는 용해도만큼 단순하지 않지만, 이 상수의 값은 일반적으로 용매에 있는 다른 종의 존재와는 독립적입니다.
기타 이론
Flory-Huggins 솔루션 이론은 폴리머의 용해성을 설명하는 이론 모델이다.Hansen 용해도 파라미터와 Hildebrand 용해도 파라미터는 용해도 예측을 위한 경험적 방법이다.융합의 엔탈피와 같은 다른 물리적 상수로부터 용해도를 예측하는 것도 가능하다.
보통 로그(Log P)로 표현되는 옥탄올-물 분할 계수는 소수성 용매(1-옥탄올)와 친수성 용매(물)에서 화합물의 미분 용해도를 측정한 값이다.이 두 값의 로그는 화합물의 친수성(또는 소수성)의 관점에서 순위를 매길 수 있게 한다.
용해와 관련된 에너지 변화는 보통 용질 몰당 용액의 엔탈피로 주어진다.
적용들
용해성은 광석 처리, 핵 재처리, 의약품 사용, 오염물질 수송 등 많은 과학 분야와 실용적 응용 분야에서 근본적으로 중요하다.
용해도(solubility)는 종종 "물질의 특징적 특성" 중 하나라고 불리며, 이는 용해도(solubility)가 물질을 기술하고, 물질의 극성을 나타내며, 다른 물질과 구별하는 데 도움을 주며, 물질의 적용에 대한 지침으로 사용된다는 것을 의미한다.예를 들어 인디고는 "물, 알코올 또는 에테르에는 용해되지 않지만 클로로포름, 니트로벤젠 또는 농축 [citation needed]황산에는 용해된다"고 기술된다.
물질의 용해성은 혼합물을 분리할 때 유용하다.예를 들어 소금(염화나트륨)과 실리카의 혼합물을 물에 녹여 미용해 실리카를 걸러내 분리해도 된다.화학성분의 합성은 실험실의 밀리그램 또는 산업계의 톤 단위로 모두 원하는 제품의 상대적인 용해도뿐만 아니라 미반응 시작 물질, 부산물 및 부생성물을 이용하여 분리를 달성한다.
또 다른 예는 브롬화 페닐마그네슘과 드라이아이스에서 벤조산을 합성하는 것이다.벤조산은 디클로로메탄이나 디에틸에테르 등의 유기용매에 용해성이 높으며, 이 유기용매와 분리 깔때기로 흔들면 유기층에서 우선적으로 용해된다.브롬화 마그네슘을 포함한 다른 반응 생성물은 수용성 층에 남아 용해성에 기초한 분리가 달성되었음을 분명히 보여줍니다.액체-액체 추출로 알려진 이 과정은 합성 화학에서 중요한 기술이다.최대한의 추출을 보장하기 위해 재활용이 사용됩니다.
미분 용해도
유동계에서는 용해성의 차이가 종종 종의 용해-침전 주도 수송을 결정한다.이것은, 시스템의 부품 마다 다른 상태가 발생했을 경우에 발생합니다.약간의 다른 조건이라도 충분한 시간이 주어진다면 상당한 영향을 미칠 수 있다.
예를 들어, 상대적으로 낮은 용해성 화합물은 더 극단적인 환경에서 용해되는 것으로 발견되어 지구 화학적, 지질학적 영향을 지구 지각에 있는 열수성 유체 활동의 결과로 초래된다.이것들은 종종 고품질의 경제 광상과 귀중하거나 반보석들의 원천이다.마찬가지로 용해도가 낮은 화합물은 오랜 시간(지질적 시간)에 걸쳐 용해되어 광범위한 동굴 시스템이나 카르스틱 지표면 등의 중대한 영향을 받는다.
물 속 이온 화합물의 용해성
일부 이온 화합물(염수)은 양전하와 음전하 사이의 인력으로 인해 물에 용해됩니다(용매화 참조).예를 들어 소금의 양이온(예: Ag+)은 부분적으로 음의 산소 원자를 HO로2 끌어들인다.마찬가지로 소금의 음이온(예를 들어− Cl)은 HO에서 부분적으로2 양의 수소를 끌어당긴다.참고: 산소 원자는 수소보다 전기 음성이 높기 때문에 부분적으로 음성이며, 그 반대도 마찬가지입니다(화학적 극성 참조).
- AgCl(s) † Ag+(aq) + Cl−(aq)
하지만, 주어진 부피의 물에서 얼마나 많은 소금이 녹을 수 있는지에는 한계가 있다.이 농도는 용해도이며 용해도 생성물 K와sp 관련이 있다.이 평형 상수는 소금의 종류(예를 들어 AgCl 대 NaCl), 온도 및 공통 이온 효과에 따라 달라진다.
순수 1리터에 녹는 AgCl의 양은 다음과 같이 계산할 수 있다.
- Ksp = [Ag+] × [Cl−] / M2 (용해도 생성물의 정의, M = mol/L)
- Ksp = 1.8 × 10−10 (용해성 생성물 표에서)
[Ag+] = [Cl−] 다른 은 또는 염화염이 없는 경우, 따라서
- [Ag+]2 = 1.8 × 10−102 M
- [Ag+] = 1.34 × 10−5 mol/L
그 결과, 상온에서 1L의 물을 1.34 × 10몰의−5 AgCl을 녹일 수 있습니다.AgCl은 다른 소금에 비해 물에 잘 녹지 않는다.예를 들어 식탁용 소금(NaCl)은 K=36이 훨씬 높기sp 때문에 용해성이 더 높다.다음 표는 다양한 이온 화합물에 대한 용해성 규칙의 개요를 보여줍니다.
| 용해성 | 불용해[22] |
|---|---|
| I족 및 NH족4+ 화합물(인산리튬 제외) | 탄산염(그룹 I, NH4+ 및 우라닐 화합물 제외) |
| 질산염 | 아황산염(I족 및 NH족4+ 화합물 제외) |
| 아세트산염(에탄산염)(Ag 화합물+ 제외) | 인산염(I족 및 NH족4+ 화합물 제외)(Li족+ 제외) |
| 염화물(염소산염 및 과염소산염), 브롬화물 및 요오드화물(Ag, Pb2+, Cu+ 및 Hg22+ 제외+) | 하이드록시드 및 산화물(그룹 I, NH4+, Ba2+, Sr2+ 및 Tl+ 제외) |
| 황산염(Ag, Pb2+, Ba2+, Sr2+ 및 Ca2+ 제외+) | 황화물(I족, II족 및 NH족4+ 화합물 제외) |
유기화합물의 용해성
위에 설명한 극성 아래에서의 원리는 용해와 마찬가지로 유기계에서의 용해성에 대한 일반적인 가이드입니다.예를 들어, 석유 젤리와 휘발유는 모두 비극성 탄화수소이기 때문에 석유 젤리는 가솔린에 용해됩니다.반면 용제의 극성이 너무 높기 때문에 에틸알코올이나 물에 녹지 않습니다.설탕은 휘발유에 비해 극성이 너무 높기 때문에 휘발유에 녹지 않는다.따라서 가솔린과 설탕의 혼합물은 여과 또는 물로 추출하여 분리할 수 있다.
솔리드 솔루션
이 용어는 종종 야금 분야에서 합금 원소가 별도의 상(相)을 형성하지 않고 모재에 용해되는 정도를 나타내기 위해 사용됩니다.용해도선(또는 곡선)은 위상 다이어그램에서 용질 첨가의 한계를 제공하는 선입니다.즉, 다른 컴포넌트에 추가할 수 있는 컴포넌트 중 솔리드 솔루션 내에 있는 컴포넌트의 최대량을 나타냅니다.고체의 결정구조에서 '용질' 원소는 격자 내의 매트릭스(예를 들어 철의 크롬 치환 위치)를 치환하거나 격자점 사이의 공간(예를 들어 철의 탄소)을 치환할 수 있다.
마이크로일렉트로닉스 제조에서 고체 용해도는 기판에 배치할 수 있는 불순물의 최대 농도를 말합니다.
고체화합물(원소와는 대조적으로)에서 용질원소의 용해성은 평형상태에서 분리되는 상에도 의존할 수 있다.예를 들어 ZnSb상에 용해되는 Sn의 양은 평형상태에서 분리되는 상이 (ZnSb43+Sn(L))인지 (ZnSnSb2+Sn(L)[23]인지에 따라 크게 달라질 수 있다.또, Sn을 용질로서 가지는 ZnSb 화합물은, 합성시의 초기 화학 조성에 따라, 용해도 한계에 이른 후의 다른 상 조합으로 분리할 수 있다.각 조합은 ZnSb에서 Sn의 다른 용해도를 생성합니다.따라서 2차 위상이 분리되는 것을 관찰한 첫 번째 사례에서 도출된 화합물에 대한 용해성 연구는 [24]용해성을 과소평가할 수 있다.평형상태에서 한번에 분리되는 최대 위상수는 Gibb의 위상규칙에 의해 결정될 수 있지만, 화학성분은 그러한 위상분리 조합의 수 자체에 제한이 없다.따라서 고형화합물의 "최대 용해도"를 실험적으로 결정하는 것은 어려울 수 있으며, 많은 시료의 평형을 필요로 한다.고체용액에 관여하는 지배적인 결정학적 결함(대부분 간질적 또는 치환점 결함)을 미리 화학적으로 직관할 수 있다면, 몇 가지 간단한 열역학적 지침을 사용하면 최대 용해도를 확립하는 데 필요한 샘플의 수를 상당히 줄일 수 있다.[25]
부조화해
많은 물질이 조화롭게 용해된다(즉, 고체와 용해된 용질의 구성이 화학적으로 일치한다).단, 일부 물질은 용액의 조성이 고체의 조성과 일치하지 않을 수 있다.이 용해는 "1차 고체"의 변화와 2차 고체상의 형성을 수반한다.그러나 일반적으로 일부 1차 고체도 남아 복잡한 용해성 평형이 형성된다.예를 들어 알바이트의 용해는 깁사이트의 [26]형성을 초래할 수 있다.
- NaAlSiO38 + H+ + 7HO2 na+ Na + Al(OH)3 + 3HSIO44
이 경우 알바이트의 용해도는 고체 대 용매비에 의존할 것으로 예상된다.이러한 용해성은 변성암의 형성을 초래하는 지질학에서 매우 중요하다.
원칙적으로, 일치와 불일치 용해가 모두 평형에서 2차 고체상을 형성할 수 있다.따라서 재료과학 분야에서는 두 사례의 용해도(solvability)가 화학조성상도에서 보다 일반적으로 설명된다.
용해도 예측
용해도(solubility)는 환경 예측, 생화학, 약국, 약품 설계, 농약 설계, 단백질 배위자 결합을 포함한 과학의 많은 측면에서 관심 있는 속성입니다.수용성은 [27][28][29]물이 수행하는 중요한 생물학적 및 운송 기능 때문에 근본적인 관심사다.또한 물의 용해성과 용매 효과에 대한 명확한 과학적 관심 외에도 용해성의 정확한 예측은 산업적으로 중요하다.분자의 용해도를 정확하게 예측하는 능력은 [30]의약품과 같은 많은 화학 제품 개발 과정에서 잠재적으로 큰 재정적 절감 효과를 나타냅니다.제약업계에서 용해도 예측은 약물 후보자의 초기 납 최적화 과정의 일부를 형성한다.용해성은 [30]제제화 과정 내내 관심사로 남아 있다.그러한 예측에는 정량적 구조-활동 관계(QSAR), 정량적 구조-특성 관계(QSPR) 및 데이터 마이닝을 포함한 많은 방법이 적용되었다.이러한 모델은 용해성의 효율적인 예측을 제공하며 현재 표준을 나타냅니다.이러한 모델은 물리적 통찰력이 부족할 수 있습니다.합리적인 비용으로 비슷한 수준의 정확도를 달성할 수 있는 물리 이론에서 확립된 방법은 과학적으로나 [31][32][33][34]산업적으로나 강력한 도구가 될 것이다.
물리 이론에서 발견된 방법들은 고전적인 열역학 개념인 열역학 주기를 사용하는 경향이 있다.사용되는 두 가지 일반적인 열역학 사이클은 승화의 자유 에너지 계산(액체 상태를 거치지 않고 고체에서 기체로)과 기체 분자를 용해시키는 자유 에너지 또는 융합의 자유 에너지(용해로 고체)와 혼합의 자유 에너지(용해로 용융)를 포함합니다.이 두 가지 프로세스를 다음 그림에 나타냅니다.
이러한 사이클은 물리적 동기 부여 용제 [32]모델을 사용한 제1원칙 예측(기본 물리 방정식을 이용한 해결) 시도에 사용되어 파라메트릭 방정식과 QSPR 모델[35][33] 및 [33]두 가지 모델의 조합을 생성한다.이러한 사이클을 사용하면 가스(승화 사이클) 또는 용해(융해 사이클)를 통해 용매 자유 에너지를 간접적으로 계산할 수 있습니다.이것은 용매의 자유 에너지를 직접 계산하는 것이 매우 어렵기 때문에 도움이 됩니다.용매의 자유 에너지는 다양한 공식을 사용하여 용해도 값으로 변환할 수 있습니다. 가장 일반적인 경우는 아래와 같습니다. 여기서 분자는 용매의 자유 에너지, R은 기체 상수, T는 켈빈 [32]단위의 온도입니다.
용해도 예측을 위한 잘 알려진 적합 방정식은 일반적인 용해도 방정식입니다.이 방정식은 Yalkowsky [36][37]등의 연구에서 비롯되었다.원래 공식은 먼저 제시되고 수정된 공식은 옥탄올의 [37]완전 혼합성에 대한 다른 가정을 취합니다.
이 방정식은 핵융합 사이클의 원리에 기초하고 있다.
「 」를 참조해 주세요.
- 겉보기 어금니
- 생물약물분류시스템
- 뒤링의 법칙 – 두 솔루션이 동일한 증기 압력을 가하는 온도 간의 선형 관계
- 파얀스-파네스-한법
- 유연한 SPC 물 모델
- 헨리의 법칙 – 용해 가스의 비율에 관한 가스 법칙
- 온수 추출
- 하이드로프
- 미셀 용매화 – 미셀에 또는 미셀에 용매화물을 함유시키는 방법
- 라울트의 법칙 – 혼합물의 증기 압력에 대한 열역학 법칙
- 솔루션 비율
- 용해도 평형
- van't Hoff 방정식 – 화학 반응의 온도와 평형 상수 사이의 관계
메모들
- ^ 리하르트에 따르면 용매 극성은 용해력으로 정의됩니다.
레퍼런스
- ^ a b IUPAC, 화학 용어집, 제2판('골드북') (1997).온라인 수정판: (2006–) "용해성"doi: 10.1351/goldbook.S05740
- ^ a b Clugston, M.; Fleming, R. (2000). Advanced Chemistry (1st ed.). Oxford: Oxford Publishing. p. 108.
- ^ J. de Swaan Arons와 G. A. M. Dien(1966) : "가스-가스 이퀄리리아"화학물리학 저널 제44권 제6호, 2322쪽. doi:10.1063/1.1727043
- ^ Tomlinson, Charles (1868-01-01). "On Supersaturated Saline Solutions". Philosophical Transactions of the Royal Society of London. 158: 659–673. doi:10.1098/rstl.1868.0028. ISSN 0261-0523. S2CID 110079029.
- ^ 클라우디우스 코르만, 데틀프 바네만, 그리고 마이클 R.Hoffmann(1988) : "양자 크기의 이산화티타늄의 준비와 특성화"물리화학 저널 제92, 제18호, 5196-5201쪽. doi:10.1021/j100329a027
- ^ Abler(2021년): "W/W(중량/중량)"온라인 페이지(Abler.com 웹사이트).2021-11-26에 접속.
- ^ I. Lee 및 J. Lee(2012): "현탁 마이크로채널 공진기를 이용한 에탄올-물 혼합물의 혼합비 및 체적 변화 측정." SENSORS, 2012년 볼륨, 1-3페이지. doi:10.1109/ICSENS.2012.641272.
- ^ "미국의 약마코페아, 32차 개정판, 그리고 국립 공식, 27차 개정판", 2009년, 페이지 1에서 12까지.
- ^ Rogers, Elizabeth; Stovall, Iris (2000). "Fundamentals of Chemistry: Solubility". Department of Chemistry. University of Wisconsin. Archived from the original on 13 April 2015. Retrieved 22 April 2015.
- ^ I.Y. Nekrasov (1996). Geochemistry, Mineralogy and Genesis of Gold Deposits. Taylor & Francis. pp. 135–136. ISBN 978-90-5410-723-1.
- ^ Hefter, G.T.; Tomkins, R.P.T (Editors) (2003). The Experimental Determination of Solubilities. Wiley-Blackwell. ISBN 978-0-471-49708-0.
{{cite book}}:first2=범용명(도움말)이 있습니다. - ^ a b 존 W. 힐, 랄프 H. 페트루치, 제너럴 케미스트리, 프렌티스 홀, 1999년 제2판
- ^ P. Cohen, ed. (1989). The ASME Handbook on Water Technology for Thermal Power Systems. The American Society of Mechanical Engineers. p. 442.
- ^ Handbook of Chemistry and Physics (27th ed.). Cleveland, Ohio: Chemical Rubber Publishing Co. 1943.
- ^ "What substances, such as cerium sulfate, have a lower solubility when they are heated?". Retrieved 28 May 2014.
- ^ Salvatore Filippone, Frank Heimanna and André Rassat (2002). "A highly water-soluble 2+1 b-cyclodextrin–fullerene conjugate". Chem. Commun. 2002 (14): 1508–1509. doi:10.1039/b202410a.
- ^ E.M. Gutman (1994). Mechanochemistry of Solid Surfaces. World Scientific Publishing Co.
- ^ G.W. Greenwood (1969). "The Solubility of Gas Bubbles". Journal of Materials Science. 4 (4): 320–322. Bibcode:1969JMatS...4..320G. doi:10.1007/BF00550401.
- ^ Kenneth J. Williamson (1994). Macroscale and Microscale Organic Experiments (2nd ed.). Lexington, Massachusetts: D. C, Heath. p. 40. ISBN 978-0-669-19429-6.
- ^ Merck Index (7th ed.). Merck & Co. 1960.
- ^ Dokoumetzidis, Aristides; Macheras, Panos (2006). "A century of dissolution research: From Noyes and Whitney to the Biopharmaceutics Classification System". Int. J. Pharm. 321 (1–2): 1–11. doi:10.1016/j.ijpharm.2006.07.011. PMID 16920290.
- ^ C. Houk; R. Post, eds. (1997). Chemistry, Concept and Problems. John Wiley & Sons. p. 121. ISBN 978-0-471-12120-6.
- ^ Wood, Maxwell; Toriyama, Michael; Dugar, Shristi; Male, James; Anand, Shashwat; Stevanović, Vladan; Snyder, Jeff (2020). "Phase Boundary Mapping of Tin-Doped ZnSb Reveals Thermodynamic Route to High Thermoelectric Efficiency". Advanced Energy Materials. 11 (20). doi:10.1002/aenm.202100181.
- ^ Tang, Yinglu; Hanus, Riley; Chen, Sin-wen; Snyder, Jeff (2015). "Solubility design leading to high figure of merit in low-cost Ce-CoSb3 skutterudites". Nature Communications. 6 (7584). doi:10.1038/ncomms8584.
- ^ Anand, Shashwat; Wolverton, Chris; Snyder, Jeff (2022). "Thermodynamic Guidelines for Maximum Solubility". Chemistry of Materials. 34 (4): 1638–1648. doi:10.1021/acs.chemmater.1c03715.
- ^ O.M. Saether; P. de Caritat, eds. (1997). Geochemical processes, weathering and groundwater recharge in catchments. Rotterdam: Taylor & Francis. p. 6. ISBN 978-90-5410-641-8.
- ^ Skyner, R.; McDonagh, J. L.; Groom, C. R.; van Mourik, T.; Mitchell, J. B. O. (2015). "A Review of Methods for the Calculation of Solution Free Energies and the Modelling of Systems in Solution" (PDF). Phys Chem Chem Phys. 17 (9): 6174–91. Bibcode:2015PCCP...17.6174S. doi:10.1039/C5CP00288E. PMID 25660403.
- ^ Tomasi, J.; Mennucci, B.; Cammi, R. (2005). "Quantum Mechanical Continuum Solvation Models". Chemical Reviews. 105 (8): 2999–3093. doi:10.1021/cr9904009. PMID 16092826.
- ^ Cramer, C. J.; Truhlar, D. G. (1999). "Implicit Solvation Models: Equilibria, Structure, Spectra, and Dynamics". Chemical Reviews. 99 (8): 2161–2200. doi:10.1021/cr960149m. PMID 11849023.
- ^ a b Abramov, Y. A. (2015). "Major Source of Error in QSPR Prediction of Intrinsic Thermodynamic Solubility of Drugs: Solid vs Nonsolid State Contributions?". Molecular Pharmaceutics. 12 (6): 2126–2141. doi:10.1021/acs.molpharmaceut.5b00119. PMID 25880026.
- ^ McDonagh, J. L. (2015). Computing the Aqueous solubility of Organic Drug-Like Molecules and Understanding Hydrophobicity. University of St Andrews. hdl:10023/6534.
- ^ a b c Palmer, D. S.; McDonagh, J. L.; Mitchell, J. B. O.; van Mourik, T.; Fedorov, M. V. (2012). "First-Principles Calculation of the Intrinsic Aqueous Solubility of Crystalline Druglike Molecules". Journal of Chemical Theory and Computation. 8 (9): 3322–3337. doi:10.1021/ct300345m. PMID 26605739.
- ^ a b c McDonagh, J. L.; Nath, N.; De Ferrari, L.; van Mourik, T.; Mitchell, J. B. O. (2014). "Uniting Cheminformatics and Chemical Theory To Predict the Intrinsic Aqueous Solubility of Crystalline Druglike Molecules". Journal of Chemical Information and Modeling. 54 (3): 844–856. doi:10.1021/ci4005805. PMC 3965570. PMID 24564264.
- ^ Lusci, A.; Pollastri, G.; Baldi, P. (2013). "Deep Architectures and Deep Learning in Chemoinformatics: The Prediction of Aqueous Solubility for Drug-Like Molecules". Journal of Chemical Information and Modeling. 53 (7): 1563–1575. doi:10.1021/ci400187y. PMC 3739985. PMID 23795551.
- ^ Ran, Y.; N. Jain; S.H. Yalkowsky (2001). "Prediction of Aqueous Solubility of Organic Compounds by the General Solubility Equation (GSE)". Journal of Chemical Information and Modeling. 41 (5): 1208–1217. doi:10.1021/ci010287z.
- ^ Yalkowsky, S.H.; Valvani, S.C. (1980). "Solubility and partitioning I: solubility of nonelectrolytes in water". Journal of Pharmaceutical Sciences. 69 (8): 912–922. doi:10.1002/jps.2600690814. PMID 7400936.
- ^ a b Jain, N.; Yalkowsky, S.H. (2001). "Estimation of the aqueous solubility I: application to organic nonelectrolytes". Journal of Pharmaceutical Sciences. 90 (2): 234–252. doi:10.1002/1520-6017(200102)90:2<234::aid-jps14>3.0.co;2-v.



 ,
, 
 압력,
압력,  상온,
상온,  용액
용액 


 온도의존상수(예를 들어 298 K의 물에서
온도의존상수(예를 들어 298 K의 물에서  분압(ATM 내),
분압(ATM 내),  액체(in/L)에 용해된 가스의
액체(in/L)에 용해된 가스의 













