겉보기 어금니 속성

혼합물 또는 용액 내 용액 성분의 겉보기 어금니 특성은 혼합물의 비이상성에 대한 각 성분의 기여를 분리하기 위한 목적으로 정의된 수량이다. 이는 해당 구성요소가 모두 솔루션에 추가되었을 때 추가된 구성요소의 몰 당 해당 솔루션 속성(예: 볼륨)의 변화를 보여준다. 다른 용액 구성요소의 특성이 추가되는 동안 일정하게 유지되는 것으로 가정할 경우, 용액에서 해당 구성요소의 어금니 특성을 나타내는 것으로 보이기 때문에 이는 명백한 것으로 설명된다. 그러나 구성요소의 외관상 어금니 특성의 값이 순수한 상태의 어금니 특성과 상당히 다를 수 있기 때문에 이러한 가정은 종종 정당화되지 않는다.

예를 들어 용매와 용액으로 식별된^[1] 두 가지 성분이 포함된 용액의 부피는 다음과 같다.

${\displaystyle V=V_{0}+{}^{{{V}_{1}\}\={\tilde{V}_{0}n_{0}+{}^{\phi }{\tilde{V}_{1}n_{1},},},}$

순수한 용제의 용질 추가하기 전에 어디 V0 용적과 V~0{\displaystyle{\tilde{V}의}_{0}}의 몰 부피(그 해결책이라고 같은 온도와 압력에서), 용매의 두더지의 n0을 몇번이나ϕ V사이 1{\displaystyle{}^{\phi}{\tilde{V}}_{1}\,}은 명백한 몰 부피. 월e 솔루트, n은₁ 용액에 있는 솔루트의 두더지 수입니다. 이 관계를 한 성분의 어금니 양과 나누면 성분의 겉보기 어금니 특성과 성분의 혼합비 사이의 관계를 얻을 수 있다.

이 방정식은 ${\displaystyle {}^{}}$ ${\displaystyle {}^{}{\stackrel{}{}}_{}}$~ ${\displaystyle 1_{\mathrm{}}}$ $displaystyle {}^{\phi }{{\tilde{V}_{1}\},}$의 정의로 작용한다$.$ 첫 번째 항은 용액이 없는 동일한 양의 용제의 부피와 같으며, 두 번째 항은 용액이 첨가될 때의 부피 변경이다. ${\displaystyle {}^{\varphi }}$ ${\displaystyle {}^{}{\stackrel{}{}}_{}}$~ ${\displaystyle 1_{\mathrm{}}}$ $displaystyle {}^{\pi }{\tilde{V}_{1}\},$ 용제의 어금니 부피가 용액의 첨가로 변경되지 않는다고 가정할 경우 용액의 어금니 부피로 간주할 수 있다$$. 그러나 이러한 가정은 종종 ${\displaystyle {아래}_{\mathrm{}}}$ 예시와 같이 비현실적으로 여겨져야 하므로 ${\displaystyle {}^{}{\stackrel{}{}}_{}}$ V${\displaystyle {\stackrel{}{}}_{}}$~ 1 $displaystyle {}^{\pi }{\tilde{V}_{1}\}}}$은(는) 겉보기 값으로만 설명된다$$.

겉보기 어금니 수량은 용매 ${\displaystyle {}^{}{\stackrel{}{}}_{}}$ ~${\displaystyle {\stackrel{}{}0}_{\mathrm{}}{}_{}}${\$displaystyle {}^{\phi }{\tilde{V}_{0}\}}}}$에 대해 유사하게 정의할 수 있다$.$ 일부 저자는 동일한 용액의 (액체) 성분 두 개 모두 겉보기 어금니 볼륨을 보고하였다.^[2][3] 이 절차는 3차 혼합물과 다중 혼합물로 확장될 수 있다.

겉보기 수량은 두더지 수 대신 질량을 사용하여 표현할 수도 있다. 이 표현은 겉보기 특정 볼륨과 같이 겉보기 특정 양을 생성한다.

${\displaystyle V=V_{0}+{}^{}{V}_{1}\{1}\{0}m_{0}\ =v_{0}m_{0}+{}^{v}_{1}m_{1}\,},}$

특정 양이 작은 문자로 표시된 경우.

겉보기(몰라) 특성은 상수가 아니라(특정 온도에서도) 구성의 함수다. 무한 희석 시 겉보기 어금니 특성과 해당 부분 어금니 특성은 동일해진다.

일반적으로 사용되는 명백한 어금니 속성은 겉보기 어금니 엔탈피, 겉보기 어금니 열 용량 및 겉보기 어금니 체적이다.

어금니와의 관계

용액의 겉보기(몰랄) 부피는 용액의 어금니 b(용액과 용제의 밀도)의 함수로 표현할 수 있다. 용액의 몰당 용액의 부피는

${\displaystyle {\frac {1}{\rho }}\왼쪽({\frac {1}{b}+M_{1}\오른쪽).}$

용액 몰당 순수 용매 부피를 빼면 겉보기 어금니 부피가 나타난다.

${\displaystyle {}^{\phi }{\tilde {V}}_{1}={\frac {V-V_{0}}{n_{1}}}=\left({\frac {m}{\rho }}-{\frac {m_{0}}{\rho _{0}^{0}}}\right){\frac {1}{n_{1}}}=\left({\frac {m_{1}+m_{0}}{\rho }}-{\frac {m_{0}}{\rho _{0}^{0}}}\right){\frac {1}{n_{1}}}=\left({\frac {m_{0}}{\rho }}-{\frac {m_{0}}{\rho _{0}^{0}}}\right){\frac {1}{n_{1}}}+{\frac {m_{1}}{\rho n_{1}}}}$

${\displaystyle{}^{\phi }{\tilde{V}_{1}={\frac {1}{b}}\{{\rho }}}-{\frac {1}{0}^{0}}}\오른쪽)+{\frac {M_{1}{1\rho}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

더 많은 용해물의 경우 위의 동등성은 용해물의 평균 어금니 질량 b를 가진_T 단일 용해물인 것처럼 수정된다.

${\displaystyle {}^{}{\stackrel{}{}}_{}V{\stackrel{}{}}_{}~{12}_{}}$${\$$}}={\frac {1}{b_{{$$T{\displaystyle }$$}}}\왼쪽({\frac {1}{\rho }-{\frac {1}{{0}^{0}}\오른쪽)+{\$frac {$M}{\rho$ $\}\}\},$ M${\displaystyle }$=${\displaystyle {}_{}{}_{}}$ ${\displaystyle y_{}}$ i ${\$i_{i}}}}}{i$}}}}}}}}}}{$i}}}}}}}}}}}}}}}}}}}}}}:{i}}}}}}}}}}}}}}}}

제품 어금니의 합계 – 이항 용액의 겉보기 어금니 부피와 위에 언급한 다중 성분 용액의 3항 단위의 겉보기 어금니 부피 사이의 제품과 동일하다.

${\displaystyle {}^{}{\stackrel{}{}}_{}V{\stackrel{}{}}_{}~{123}_{}}$${\displaystyle {}^{\phi }{\tilde {V}_{123}$$}}(b_{1}+b_{2}+b_{3}+...)=b_{1}{}^{{}^{\phi }{\tilde{V}_{1}+b_{2$$}$$}}{}^{\phi }{\tilde {V}_{2}+b_{3$$}$$}}{}^{\phi }{\tilde{V}_{3}+...$$}$,

혼합비와의 관계

혼합물 성분의 겉보기 어금니와 어금니 혼합비 사이의 관계는 정의 관계를 나누어 얻을 수 있다.

${\displaystyle V=V_{0}+{}^{{{V}_{1}\}\={\tilde{V}_{0}n_{0}+{}^{\phi }{\tilde{V}_{1}n_{1},},},}$

두더지 수에 따라 달라진다. 이는 다음과 같은 관계를 제공한다.

${\displaystyle {}^{\phi }{\tilde {V}}_{1}={\frac {V}{n_{1}}}-{\tilde {V}}_{0}{\frac {n_{0}}{n_{1}}}={\frac {V}{n_{1}}}-{\tilde {V}}_{0}r_{01}}$

부분(몰라) 수량과의 관계

부분 어금니 양과 겉보기 어금니 양 사이의 대조적인 정의에 유의하십시오: 부분 어금니 볼륨 $V{\displaystyle \stackrel{}{{}_{}}}$ ${\displaystyle \stackrel{}{{0\mathrm{}}_{}}}$의 경우${\displaystyle ,}$ ${\displaystyle \stackrel{}{{V\mathrm{}}_{}}}$ ${\displaystyle 1\stackrel{}{{}_{}}}$ $"{\$ 부분 파생 모델에 의해 정의됨

${\displaystyle {\bar {V_{0}}}={\Big (}{\frac {\partial V}{\partial n_{0}}}{\Big )}_{T,p,n_{1}},{\bar {V_{1}}}={\Big (}{\frac {\partial V}{\partial n_{1}}}{\Big )}_{T,p,n_{0}}}$,

one can write ${\displaystyle dV={\bar {V_{0}}}dn_{0}+{\bar {V_{1}}}dn_{1}}$, and so ${\displaystyle V={\bar {V_{0}}}n_{0}+{\bar {V_{1}}}n_{1}}$ always holds. 이와는 대조적으로 겉보기 어금니 부피의 정의에서는 순수 용매의 어금니 $부피$인 V${\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 0_{\mathrm{}}}$ ${\$을 대신 사용하므로 다음과 같이 표기할 수 있다.

${\displaystyle \stackrel{}{V_{}}}$ ${\displaystyle \stackrel{}{{0\mathrm{}}_{}}~}$ = (${\displaystyle \partial \frac{\mathrm{}}{}}$ ${\displaystyle \frac{V}{}}$ ${\displaystyle \frac{\mathrm{}{}_{}}{}}$ ${\displaystyle \frac{{0\mathrm{}}_{}}{}{}_{}}$) T${\displaystyle {}_{}}$, ${\displaystyle p_{}}$, ${\displaystyle {{n\mathrm{}}_{}}_{}}$ ${\displaystyle {1{}_{}}_{}}$= 0 ${\$0}}},},},},},},},}, {n.

비교해서 즉 용매의 부피가 변하지 않는다고 가정하고, 용매의 두더지 수가 정확히 0("어금 부피")인 부분 어금니를 사용한다. 따라서 겉보기 어금니 볼륨 ${\displaystyle {}^{}}$ ${\displaystyle {}^{}{\stackrel{}{}}_{}}$~ ${\displaystyle 1_{\mathrm{}}}$ ${\$$1}},$

${\displaystyle V=V_{0}+{}^{\phi }{V}_{1}\ ={\tilde {V}}_{0}n_{0}+{}^{\phi }{\tilde {V}}_{1}n_{1}\,}$,

$V{\displaystyle {}_{}}$ ${\$라는 용어는 순수 용매에 기인하며, "좌측" 초과 볼륨인 , ${\displaystyle {V\mathrm{}}_{}}$ ${\displaystyle {}^{}{}_{}}$ ${\$는$$용매에서 기인한 것으로 간주된다$$. At high dilution with ${\displaystyle n_{0}\gg n_{1}\approx 0}$, we have ${\displaystyle {\tilde {V_{0}}}\approx {\bar {V_{0}}}}$, and so the apparent molar volume and partial molar volume of the solute also converge: ${\displaystyle$${}^{\phi }{\tilde{V}_{1}\약간${\$bar{V}_{1$

정량적으로 부분 어금니 특성과 겉보기 어금니 특성의 관계는 겉보기 수량과 어금니의 정의에서 도출될 수 있다. 볼륨의 경우,

${\displaystyle {\v_{1}}={}^{\phi }{}{{}}{\tilde{V}}+b{1}+b{\prac{}^{\phi }{\tilde{V}}}{\partial b}}}.}$

전해질의 활성계수와 용해 셸 수와의 관계

농축액에서 용해된 전해액의 겉보기 어금니 부피와 용제(물)의 어금니 부피 사이의_a r 비율은 전해액의$$ 활성계수 $\gamma {\displaystyle {}_{}}$ ${\$와 용해 셸 번호 h:^[4]

${\displaystyle \ln \gamma _{s}={\frac {h-\nu }{\nu }}\ln(1+{\frac {br_{a}}{55.5}})-{\frac {h}{\nu }}\ln(1-{\frac {br_{a}}{55.5$$}}}}}+{\frac {br_{a}(r_{a}+h-\nu )}{55.5({1+{\frac{br_}}{55.5$$)$$}})}}}$,

여기서 ν은 전해질의 분리에 의한 이온의 수이고, b는 위와 같은 어금니이다.

예

전해질

겉보기 어금니 소금의 양은 보통 고형 소금의 어금니 부피보다 적다. 예를 들어 솔리드 NaCl의 경우 몰당 용적은³ 27cm이지만 낮은 농도의 겉보기 어금니 용적은 16.6cc/mole에 불과하다. 실제로 일부 수용성 전해질에는 음의 겉보기 어금니 부피가 있다: NaOH -6.7, LiOH -6.0, NaCO₂₃ -6.7 cm³/mole.^[5] 이는 주어진 양의 물에 있는 그들의 용액은 같은 양의 순수한 물보다 부피가 작다는 것을 의미한다. (그러나 효과는 작다.) 물리적인 이유는 가까운 물 분자가 이온에 강하게 끌려서 공간을 적게 차지하기 때문이다.

알코올

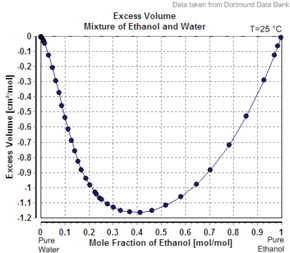
두 번째 성분의 겉보기 어금니 부피의 또 다른 예는 순수한 물질로서 어금니 부피보다 적다. 예를 들어 20 mass percents 에탄올에서 용액은 20 °C에서 kg당 1.0326리터의 부피를 가지는 반면, 순수한 물은 1.0018 L/kg(1.0018 cc/g)이다.^[6] 첨가된 에탄올의 겉보기 부피는 1.0326 L – 0.8 kg x 1.0018 L/kg = 0.2317 L이다. 에탄올의 몰 개수는 0.2 kg / (0.04607 kg/mol) = 4.341 mol이므로 겉보기 어금니 부피는 0.2317 L / 4.341 mol = 0.0532 L / mol = 53.2 cc/mole (1.16 cc/g)이다. 그러나 순수 에탄올은 이 온도 58.4cc/mole(1.27cc/g)에서 어금니 부피가 있다.

솔루션이 이상적이라면, 그 용량은 혼합되지 않은 구성 요소의 합이 될 것이다. 0.2 kg 순수 에탄올의 부피는 0.2 kg x 1.27 L/kg = 0.254 L이고, 0.8 kg 순수수의 부피는 0.8 kg x 1.0018 L/kg = 0.80144 L이므로 이상적인 용액 부피는 0.254 L + 0.80144 L = 1.055 L이다. 용액의 비이상성은 혼합시 결합계통의 부피에서 약간 감소(대략 1.055 L/kg이 아닌 1.2%, 1.0326)하여 반영된다. 에탄올 비율이 100%로 올라갈수록 겉보기 어금니 부피는 순수한 에탄올의 어금니 부피까지 증가한다.

전해질 – 비전기적 시스템

겉보기 수량은 염분 및 염분과 같은 상호작용을 보여주는 비전기적 시스템인 전해질에서 상호작용을 밑줄로 표시할 수 있지만, 특히 온도에 대한 이온 상호작용에 대한 통찰력을 제공한다.

다중 성분 혼합물 또는 용액

다중 요소 용액의 경우, 명백한 어금니 성질은 여러 가지 방법으로 정의될 수 있다. For the volume of a ternary (3-component) solution with one solvent and two solutes as an example, there would still be only one equation ${\displaystyle (V={\tilde {V}}_{0}n_{0}+{}^{\phi }{\tilde {V}}_{1}n_{1}+{}^{\phi }{\tilde {V}}_{2}n_{2})}$$$, 이것은 두 개의 겉보기 볼륨을 결정하기에 불충분하다. (이것은 물질의 잘 정의된 집중적인 특성인 부분 어금니 특성과 대조적이며, 따라서 다중 요소 시스템에서는 명확하지 않게 정의된다. 예를 들어, 부분 어금니 볼륨은 각 성분 i에 ${\displaystyle \stackrel{}{{대해}_{}}}$ $Vi{\displaystyle \stackrel{}{{}_{}}}$ ${\displaystyle \stackrel{}{{}_{}}}$= (${\displaystyle \mathrm{\partial }}$ ${\displaystyle V}$/ ${\displaystyle \partial \mathrm{}{n}_{}}$ i${\displaystyle {}_{}{}_{}}$) T${\displaystyle {}_{}}$, ${\displaystyle p_{}}$, ${\displaystyle {{}_{}}_{}}$ ${\displaystyle {j_{}}_{}}$ ${\displaystyle {{\ne }_{}}_{}}$ i ${\$neq})로$정의된다.$

3차 수용액에 대한 설명 중 하나는 용액의 가중 평균 외관 어금니 부피만을 고려하며,^[7] 이는 다음과 같이 정의된다.

${\displaystyle {}^{\phi }{\tilde {V}}(n_{1},n_{2})={}^{\phi }{\tilde {V}}_{12}={\frac {V-V_{0}}{n_{1}+n_{2$$}}}}$,

여기서 $V{\displaystyle }$ ${\displaystyle V}$은(는) 솔루션 볼륨이고 $V{\displaystyle {}_{}}$ ${\displaystyle {0\mathrm{}}_{}}$ ${\$ 순수의 볼륨이다$$. 이 방법은 성분이 3개 이상인 혼합물에 대해 확장할 수 있다.^[8]

${\displaystyle {}^{}\stackrel{}{}V\stackrel{}{}~(\; n{1\mathrm{}}_{},{}_{}{}_{}{2\mathrm{}}_{},{}_{}n{3\mathrm{}}_{},.)={}^{}{\stackrel{}{}}_{}V{\stackrel{}{}}_{}~{123}_{}}$$displaystyle {}^{\pi }{\tilde{V}}(n_{1},n_{2},n_{3})$$={}^{\phi }{\tilde{V}_{123..$$}}={\frac {V-V_{0}}{n_{1}+{1}+n_{2}+n_{$$3}+...$$}}}$,

제품 어금니의 합계 – 이항 용액의 겉보기 어금니 부피와 위에 언급한 다중 성분 용액의 3항 단위의 겉보기 어금니 부피 사이의 제품과 동일하다.

${\displaystyle {}^{}{\stackrel{}{}}_{}V{\stackrel{}{}}_{}~{123}_{}}$${\displaystyle {}^{\phi }{\tilde {V}_{123}$$}}(b_{1}+b_{2}+b_{3}+...)=b_{1}{}^{{}^{\phi }{\tilde{V}_{1}+b_{2$$}$$}}{}^{\phi }{\tilde {V}_{2}+b_{3$$}$$}}{}^{\phi }{\tilde{V}_{3}+...$$}$,

또 다른 방법은 3차 시스템을 유사수치로 취급하고 물과 다른 용액을 모두 포함하는 2진 시스템을 참조하여 각 용액의 겉보기 어금니 부피를 정의하는 것이다.^[9] 이때 두 용액의 겉보기 어금니 체적은 각각 다음과 같다.

${\displaystyle {}^{\phi }{\tilde {V}}_{1}={\frac {V-V(solvent+solute\ 2)}{n_{1}}}}$ and ${\displaystyle {}^{\phi }{\tilde {V}}_{2}={\frac {V-V(solvent+solute\ 1)}{n_{2}}}}$

용제의 겉보기 어금니 부피는 다음과 같다.

${\displaystyle {}^{\phi }{\tilde{V}_{0}={\frac {V-V(솔루트\ 1+솔루트\ 2)}{n_{0}}}}}}}}$

그러나 이는 체적 특성에 대한 불만족스러운 설명이다.^[10]

두 구성 요소나 solutes의 명백한 몰 부피 pseudocomponent으로 여겨지ϕ V~ 12{\displaystyle{}^{\phi}{\tilde{V}}_{12}}또는ϕ V~ 나는 j{\displaystyle{}^{\phi}{\tilde{V}}_{ij}} 있지 않을 것을 혼동과 볼륨의 부분 2진 조합으로 하나의 공통 요소 Vij, Vjk.믹스특정 혼합비에서 ed는 특정 3차 혼합물 V 또는 V를_ijk 형성한다.^{[clarification needed]}

물론 혼합물의 다른 성분에 관한 성분의 보충 부피는 다음과 같이 주어진 성분의 이항 혼합물의 부피와 혼합물의 부피 사이의 차이로 정의될 수 있다.

${\displaystyle {}^{c}{\tilde{V}}{2}={\frac {V-V_{01}}{n_{2}}:}$

설탕이나 소금과 같은 고체를 녹일 수 있거나 그렇지 않은 액체 혼합물(물이나 에탄올)의 경우처럼 어떤 것이 용매이고 어떤 것이 용매인지를 규정하는 엄격한 방법이 없는 상황이 있다. 이러한 경우 명백한 어금니 성질은 혼합물의 모든 성분에 귀속될 수 있으며 반드시 귀속되어야 한다.

참고 항목

• 부피분수
• 이상적인 솔루션
• 정규용액
• 엔탈피 용액 변화
• 혼합 엔탈피
• 블록 설계
• 희석열
• 수화 에너지
• 이온수송번호
• 용배 껍데기
• 부분 어금니 속성
• 어금니수량초과
• 솔팅 인
• 3차 플롯
• 열역학 활동

참조

외부 링크

• 겉보기 어금니 속성: 솔루션: 배경
• LiI 또는 ZnCl2 에탄올 용액의 (p,p,properties,T) 특성 및 외관상 어금니 부피
• T = (288.15, 298.15, 313.15, 328.15) K 및 p = 0.1MPa에서 Pr(NO3)3(aq), Gd(NO3)3(aq), Ho(NO3)3(aq) 및 Y(NO3)3(aq)의 외관 어금니 용적 및 외관 어금니 열 용량
• 전해질 외관 특성에 대한 동위원소 효과