생물통계학

Biostatistics
"바이오메트리"는 여기서 리다이렉트됩니다.내재된 신체적 또는 행동적 특성에 기초한 사람의 자동 인식은 생체측정학을 참조하십시오.
학술 저널에 대해서는 생물 통계(저널)를 참조해 주세요.

생물통계학(biostatistics)은 생물학에서 다양한 주제에 통계적 방법을 개발하고 적용하는 것을 말한다.여기에는 생물학적 실험의 설계, 해당 실험의 데이터 수집 및 분석, 결과의 해석이 포함됩니다.

역사

생물통계학 및 유전학

생물통계학적 모델링은 수많은 현대 생물학 이론의 중요한 부분을 형성합니다.유전학 연구는 시작부터 관찰된 실험 결과를 이해하기 위해 통계적 개념을 사용했다.일부 유전학자들은 심지어 방법과 도구의 개발에 통계적 발전에 기여하기도 했다.그레고르 멘델은 완두콩 과의 유전적 분리 패턴을 조사하는 유전학 연구를 시작했고 수집된 데이터를 설명하기 위해 통계를 사용했습니다.1900년대 초 멘델의 유전학 연구가 재발견된 이후 유전학과 진화론 사이에 이해의 차이가 있었다.프란시스 갈튼은 멘델의 발견을 인간 데이터로 확장하려고 노력했고 각각의 조상이 무한 급수를 구성하는 유전의 일부를 가진 다른 모델을 제안했다.그는 이것을 "조상 유전의 법칙"이라고 불렀다.그의 생각은 멘델의 결론에 따르던 윌리엄 베이츠슨에 의해 강하게 반대되었는데, 그는 유전적인 유전은 부모들로부터만, 그들 각각의 절반으로부터만 나온다는 것이었다.이것은 라파엘 웰던, 아서 두킨필드 다르시어, 칼 피어슨처럼 갈튼의 생각을 지지했던 생체 인식학자들과 찰스 데이븐포트와 빌헬름 요한센과 같은 베이튼의 생각을 지지했던 멘델리안들 사이의 활발한 논쟁으로 이어졌다.나중에 생체인식학자들은 다른 실험에서 갈튼의 결론을 재현할 수 없었고 멘델의 생각이 우세했다.1930년대까지, 통계적 추론을 바탕으로 만들어진 모델들은 이러한 차이를 해결하고 신다르윈식 현대 진화적 합성을 생산하는 데 도움을 주었다.

이러한 차이를 해결하는 것은 또한 집단 유전학의 개념을 정의할 수 있게 했고 유전학과 진화를 하나로 묶었다.집단 유전학의 확립과 이 합성에 있어 세 명의 주요 인물들은 모두 통계에 의존했고 생물학에서 그 사용을 발전시켰다.

이것들과 다른 생물통계학자, 수리 생물학자, 그리고 통계적으로 성향이 있는 유전학자들은 진화 생물학과 유전학을 양적으로 모델링되기 시작할 수 있는 일관성 있고 일관된 전체로 결합하는 것을 도왔다.

이러한 전체적인 발전과 병행하여, On Growth and Form의 D'Arcy Thompson의 선구적인 연구는 또한 생물학적 연구에 양적 규율을 추가하는 데 도움을 주었다.

통계적 추론의 근본적인 중요성과 빈번한 필요성에도 불구하고, 그럼에도 불구하고 생물학자들 사이에서는 질적으로 분명하지 않은 결과를 불신하거나 비난하는 경향이 있었을 수 있다.일화는 토마스 헌트 모건이 칼텍에서 프리든 계산기를 사용하는 것을 금지한 것을 묘사하며, "글쎄요, 저는 1849년 새크라멘토 강둑에서 금을 찾는 사람 같아요.약간의 지능만 있으면 큰 금덩어리를 주울 수 있어그리고 그렇게 할 수 있는 한, 우리 부서의 어느 누구도 사광 [2]채굴에 부족한 자원을 낭비하도록 내버려두지 않을 것입니다."

연구 계획

생명과학에 관한 모든 연구는 우리가 가지고 있을지도 모르는 과학적 질문에 답하기 위해 제안된다.이 질문에 확실하게 답하기 위해서는 정확한 결과가 필요합니다.주요 가설과 연구 계획의 올바른 정의는 현상을 이해하는 데 있어 결정을 내리는 동안 오류를 줄일 것이다.연구 계획에는 연구 질문, 테스트할 가설, 실험 설계, 데이터 수집 방법, 데이터 분석 관점 및 관련 비용이 포함될 수 있다.랜덤화, 복제 및 국소 제어라는 실험 통계의 세 가지 기본 원칙을 기반으로 연구를 수행하는 것이 중요합니다.

조사 질문

연구 질문은 연구의 목적을 정의할 것이다.이 연구는 질문에 의해 주도될 것이기 때문에 간결해야 하며, 동시에 과학과 지식 그리고 그 분야를 향상시킬 수 있는 흥미롭고 참신한 주제에 초점을 맞춰야 한다.과학적 질문을 하는 방법을 정의하기 위해서는 철저한 문헌 검토가 필요할 수 있다.그래서 그 연구는 과학계에 [3]가치를 더하는 데 유용할 수 있다.

가설의 정의

일단 연구의 목적이 정의되면, 연구 질문에 대한 가능한 답을 제안할 수 있고, 이 질문을 가설로 바꿀 수 있다.주요 제안은 귀무 가설(H0)이라고 불리며, 대개 깊은 문헌 검토에 의해 뒷받침되는 주제에 대한 영구적인 지식이나 현상의 명백한 발생에 기초한다.테스트 대상 데이터에 대한 표준 예상 답안이라고 할 수 있습니다.일반적으로 H는O 사이에 아무런 연관성이 없다고 가정합니다. 반면, 다른 가설은 H의O 부정입니다.치료와 결과 사이에 어느 정도 연관성이 있다고 가정합니다.하지만, 그 가설은 질문 연구와 예상된 답변과 예상치 못한 [3]답변에 의해 뒷받침된다.

예를 들어, 두 개의 다른 식단 체계에서 유사한 동물(예: 쥐)의 그룹을 생각해 보십시오.연구 질문은 다음과 같습니다. 가장 좋은 식단은 무엇인가?이 경우 H는0 마우스 대사에서 두 식단 사이에 차이가 없다는 것이고(H01: μ2 = μ), 대안 가설은 식단이 동물 대사에 다른 영향을 미친다는 것이다(H11: μ μ2 μ μ μ μ μ).

이 가설은 연구자가 주요 질문에 대한 자신의 관심사에 따라 정의한다.이외에도 대립 가설은 둘 이상의 가설일 수 있습니다.관측된 매개변수 간의 차이뿐만 아니라 차이 정도(즉, 더 높거나 더 짧음)를 가정할 수 있다.

샘플링

보통 연구는 모집단에 대한 현상의 영향을 이해하는 것을 목표로 한다.생물학에서 개체군은 특정 시간에 특정 영역에 있는 특정 종의 모든 개체로 정의됩니다.생물 통계학에서, 이 개념은 연구가 가능한 다양한 수집으로 확장된다.생물통계학에서는 개체뿐만 아니라동물의 게놈 전체 또는 정자세포 전체 또는 식물의 잎 전체 면적을 나타냅니다.

인구의 모든 요소에서 측정이 가능한 것은 아니다.그렇기 때문에 샘플링 프로세스는 통계적 추론에 매우 중요합니다.표본 추출은 모집단 전체의 대표 부분을 무작위로 취득하여 모집단에 대한 사후 추론을 하는 것으로 정의된다.따라서 표본이 [4]모집단에서 가장 큰 변동성을 포착할 수 있습니다.표본 크기는 사용 가능한 자원에 대한 조사 범위 때문에 몇 가지 사항에 의해 결정됩니다.임상연구에서는 열등감, 등가성, 우등성이 표본크기의 결정의 [3]열쇠가 된다.

실험 설계

실험 설계는 실험 통계의 기본 원칙을 지지한다.모든 실험 그림에 처리를 랜덤하게 할당하는 세 가지 기본 실험 설계가 있습니다.완전 랜덤화 설계, 랜덤화 블럭 설계 및 요인 설계입니다.치료법은 실험 내부에서 여러 가지 방법으로 배열될 수 있습니다.농업에서는 환경이 플롯(식물, 가축, 미생물)에 큰 영향을 미치기 때문에 올바른 실험 설계는 좋은 연구의 근원이며 연구 내 처리의 배열이 필수적이다.이러한 주요 배열은 문헌에서 "격자", "불완전한 블록", "분할도", "증강된 블록" 등의 이름으로 찾을 수 있습니다.모든 설계에는 추론 중에 오차 추정을 제공하기 위해 연구자가 결정한 관리도가 포함될 수 있습니다.

임상 연구에서 샘플은 보통 다른 생물학적 연구보다 작으며, 대부분의 경우 환경 영향을 통제하거나 측정할 수 있다.무작위 대조군 임상시험을 사용하는 것이 일반적이며, 여기서는 결과가 환자-대조군 또는 [5]코호트와 같은 관찰 연구 설계와 비교된다.

데이터 수집

데이터 수집 방법은 표본 크기와 실험 설계에 큰 영향을 미치기 때문에 연구 계획에서 고려해야 합니다.

데이터 수집은 데이터 유형에 따라 달라집니다.질적 데이터의 경우,[6] 수집은 발생 수준을 분류하기 위해 점수 기준을 사용하여 질병의 존재 또는 강도를 고려하여 구조화된 설문지를 사용하거나 관찰을 통해 수행될 수 있다.정량적 데이터의 경우 계측기를 이용하여 수치정보를 측정하여 수집한다.

농업 및 생물학 연구에서 산출량 데이터와 그 구성요소는 미터법으로 얻을 수 있다.그러나 플레이트의 해충 및 질병 손상은 손상 수준에 대한 점수 척도를 고려하여 관찰을 통해 얻습니다.특히 유전자 연구에서 표현형 및 유전자형을 위한 높은 처리량 플랫폼으로 현장 및 실험실의 데이터 수집을 위한 최신 방법을 고려해야 한다.이러한 도구를 사용하면 대규모 실험을 수행할 수 있으며, 인간 기반 데이터 수집 방법보다 짧은 시간에 많은 그림을 평가할 수 있습니다.마지막으로, 수집된 모든 데이터는 추가 분석을 위해 정리된 데이터 프레임에 저장해야 합니다.

분석 및 데이터 해석

설명 도구

주요 기사:기술 통계

데이터는 꺽은선형 차트, 막대 차트, 히스토그램, 산점도 등과 같은 표 또는 그래픽 표현을 통해 표시할 수 있습니다.또한 중심 경향과 변동성의 측정은 데이터의 개요를 설명하는 데 매우 유용할 수 있습니다.몇 가지 예를 들어보겠습니다.

주파수 테이블

테이블 유형 중 하나는 빈도 테이블로, 행과 열에 배열된 데이터로 구성됩니다. 여기서 빈도는 데이터의 발생 횟수 또는 반복 횟수입니다.빈도는 다음과 같습니다.[7]

Absolute: 결정된 값이 나타나는 횟수를 나타냅니다.

상대: 절대 주파수를 총수로 나눈 값

다음 예에서는 같은 유기체의 10개의 오퍼론에 유전자의 수가 있습니다.

유전자 = {2,3,4,5,3,3,3,3,3,4}
유전자 번호 절대 주파수 상대 주파수
1 0 0
2 1 0.1
3 6 0.6
4 2 0.2
5 1 0.1

선 그래프

그림 A: 선 그래프의 예시.브라질의 출산율(2010-2016년)[8]그림 B: 막대 그래프의 예2010년부터 2016년까지 12월의 브라질 출생률.그림 C: 박스 플롯의 예: 8개의 다른 유기체의 프로테옴 내 글리신 수(A-H), 그림 D: 산란도의 예.

선 그래프는 시간 등의 다른 메트릭에 대한 값의 변동을 나타냅니다.일반적으로 값은 수직축에 표시되고 시간 변동은 수평축에 [9]표시됩니다.

막대 그래프

막대 차트는 값을 나타내는 높이(수직 막대) 또는 너비(수평 막대)를 나타내는 막대로 범주형 데이터를 보여주는 그래프입니다.막대 차트는 표 [9]형식으로도 나타낼 수 있는 이미지를 제공합니다.

막대 그래프의 예에서는, 2010년부터 [8]2016년까지의 12월의 브라질 출산율이 나와 있습니다.2016년 12월의 급격한 하락은 브라질 출생률에서 지카 바이러스의 발생을 반영한다.

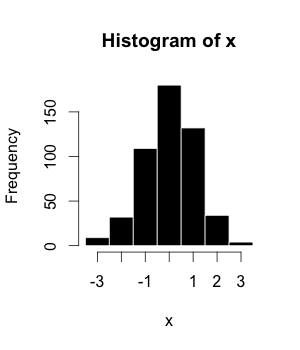
히스토그램

히스토그램 예제입니다.

히스토그램(또는 빈도 분포)은 데이터 집합을 도표화하여 균일한 클래스 또는 불균일한 클래스로 나눈 그래픽 표현입니다.그것은 [10]Karl Pearson에 의해 처음 소개되었다.

산점도

산점도란 데카르트 좌표를 사용하여 데이터 집합의 값을 표시하는 수학 다이어그램입니다.산점도에서는 데이터를 점 세트로 나타내며, 각각은 수평 축의 위치를 결정하는 한 변수의 값과 수직 [11]축의 다른 변수의 값을 나타냅니다.이러한 그래프를 산포 그래프, 산포 차트, 산포도 또는 [12]산포 다이어그램이라고도 합니다.

의미하다

주요 기사:평균

산술 평균은 값 집합(1 + 2 + + + { style { _ {1 + _ {2} + x _ {3} + \ +_ { })의 합계를 이 집합의 수(n \ { n )로 나눈 것입니다.

중앙값

주요 기사:중위수

중위수는 데이터 집합의 중간에 있는 값입니다.

모드

주요 기사:모드(통계정보)

모드는 가장 [13]자주 나타나는 데이터 세트의 값입니다.

평균, 중위수 및 모드 비교
값 = { 2,3,3,3,3,4,11}
유형 예 결과
의미하다( 2 + 3 + 3 + 3 + 3 + 3 + 4 + 4 + 11 ) / 9 4
중앙값 2, 3, 3, 3, 3, 3, 4, 11 3
모드 2, 3, 3, 3, 3, 3, 4, 11 3

상자 그림

상자 그림은 숫자 데이터 그룹을 그래픽으로 표현하는 방법입니다.최대값과 최소값은 선으로 나타내며 사분위간 범위(IQR)는 데이터의 25~75%를 나타냅니다.특이치는 원으로 표시할 수 있습니다.

상관 계수

두 가지 다른 종류의 데이터 간의 상관관계는 그래프(예: 산점도)로 추론할 수 있지만, 수치 정보를 통해 이를 검증해야 한다.따라서 상관 계수가 필요합니다.이 [9]값은 연관성의 강도를 나타내는 수치입니다.

Pearson 상관 계수

values의 서로 다른 값에 대한 Pearson 상관 관계를 나타내는 산포도입니다.

Pearson 상관 계수는 X와 Y라는 두 변수 간의 연관성을 측정하는 측도입니다.일반적으로 모집단의 경우 θ(rho)와 표본의 경우 r로 표현되는 이 계수는 -1과 1 사이의 값을 가정합니다. 여기서 θ = 1은 완벽한 양의 상관 관계를 나타내며 θ = -1은 완벽한 음의 상관 관계를 나타내며 θ = 0은 선형 [9]상관 관계가 없습니다.

추리통계

주요 기사:통계적 추론

추정 및/또는 가설 검정을 통해 미지의 모집단에 대한 추론을 수행하는[14] 데 사용됩니다.즉, 관심 모집단을 기술하기 위한 매개변수를 얻는 것이 바람직하지만, 데이터가 한정되어 있기 때문에 이를 추정하기 위해서는 대표 표본을 사용할 필요가 있다.이것에 의해, 이전에 정의된 가설을 시험해, 그 결론을 전체 모집단에 적용할 수 있다.평균의 표준 오차는 [4]추론을 수행하는 데 중요한 변동성의 측도입니다.

가설 테스트는 "연구 계획" 섹션에서 설명한 바와 같이 연구 질문에 대한 답을 목표로 하는 모집단에 대한 추론을 하기 위해 필수적이다.작성자는 설정할 [4]4가지 단계를 정의했습니다.

  1. 테스트할 가설: 앞에서 설명한 바와 같이 테스트할 귀무 가설(H0)의 정의와 대체 가설로 작업해야 합니다.단, 이들은 실험을 실시하기 전에 정의되어야 합니다.
  2. 중요도 수준 및 결정 규칙: 결정 규칙은 중요도 수준, 즉 허용 오류율(α)에 따라 달라집니다.검정 통계와 비교할 때 통계적 유의성을 결정하는 임계값을 정의한다고 생각하기 쉽습니다.따라서 실험 전에 α도 미리 정의해야 합니다.
  3. 실험 및 통계 분석:이때 적절한 실험 설계에 따라 실제로 실험이 구현되고 데이터가 수집되며 보다 적합한 통계 테스트가 평가됩니다.
  4. 추론:p-값과 α의 비교가 가져온 증거를 바탕으로 귀무 가설이 기각되거나 기각되지 않을 때 만들어집니다.H를 기각하지0 못한 것은 H의 거부를 뒷받침할 충분한 증거가 없다는 것을 의미할 뿐 이 가설이 사실이 아니라는 지적이다.

신뢰 구간은 특정 신뢰 수준에서 실제 매개 변수 값을 포함할 수 있는 값의 범위입니다.첫 번째 단계는 모집단 모수의 최량 치우침 추정치를 추정하는 것입니다.구간의 상한 값은 이 추정치의 합과 평균의 표준 오차 및 신뢰 수준 간의 곱으로 구합니다.낮은 값의 계산은 비슷하지만, 합계 대신 감산을 [4]적용해야 합니다.

통계적 고려사항

전원 오류 및 통계 오류

가설을 검정할 때 두 가지 유형의 통계적 오류가 발생할 수 있습니다.타입 I 에러와 타입 II 에러.I형 오류 또는 거짓 양성은 참 귀무 가설을 잘못 기각한 것이고, II형 오류 또는 거짓 음성은 거짓 귀무 가설을 기각하지 못한 것입니다.α로 표시된 유의 수준은 유형 I 오류율이며 테스트를 수행하기 전에 선택해야 합니다.유형 II 오류율은 β로 나타내며, 테스트의 통계적 검정력은 1 - β이다.

p값

p-값은 귀무 가설(H0)이 참이라고 가정할 때 관측된 값보다 극단적이거나 극단적인 결과를 얻을 확률입니다.계산된 확률이라고도 합니다.일반적으로 p-값을 유의 수준(α)과 혼동하지만 α는 유의한 결과를 호출하기 위한 사전 정의된 임계값입니다.p가 α보다 작으면 귀무 가설(H0)이 [15]기각됩니다.

복수 테스트

동일한 가설을 가진 여러 검정의 경우, 거짓 양성(가족별 오류율)의 발생 확률이 증가하고 이러한 발생을 제어하기 위해 몇 가지 전략이 사용됩니다.이것은 일반적으로 귀무 가설을 기각하기 위해 더 엄격한 분계점을 사용하여 달성됩니다.본페로니 보정은 α*로 표시된 허용 가능한 전역 유의 수준을 정의하고 각 테스트를 α = α*/m의 값과 개별적으로 비교합니다.이렇게 하면 모든 m개 검정의 패밀리별 오류율이 α* 이하가 됩니다.m이 크면 Bonferroni 보정이 지나치게 보수적일 수 있습니다.Bonferroni 보정의 다른 방법은 FDR(False Discovery Rate)을 제어하는 것입니다.FDR은 잘못된(잘못된) 기각된 귀무 가설(일명 발견)의 예상 비율을 제어합니다.이 절차에 따라 독립된 테스트에서는 false discovery rate가 최대 q*가 됩니다.따라서 FDR은 Bonferroni 보정보다 덜 보수적이며 잘못된 양의 [16]값을 더 많이 사용하여 더 많은 검정력을 가집니다.

잘못된 사양 및 견고성 검사

시험 중인 주요 가설(예: 치료와 결과 사이에 연관성이 없음)은 귀무 가설의 일부이기도 한 다른 기술적 가정(예: 결과의 확률 분포 형태)을 동반하는 경우가 많다.기술적 가정이 실제로 위반되면 주요 가설이 참일지라도 귀무 가설이 자주 기각될 수 있습니다.이러한 불합격은 모델의 잘못된 [17]사양에 의한 것으로 알려져 있습니다.기술적 가정이 약간 변경되었을 때 통계적 테스트의 결과가 변경되지 않는지 검증하는 것(이른바 건전성 검사)은 잘못된 사양에 대항하는 주요 방법이다.

모델 선택 기준

모델 기준을 선택하면 실제 모델에 더 가까운 모델이 선택되거나 모형화됩니다.Akaike의 정보 기준(AIC)과 베이지안 정보 기준(BIC)은 점근적으로 효율적인 기준의 예이다.

개발 및 빅데이터

최근의 발전은 생물 통계학에 큰 영향을 끼쳤다.두 가지 중요한 변화는 높은 스루풋 규모로 데이터를 수집할 수 있는 기능과 계산 기술을 사용하여 훨씬 더 복잡한 분석을 수행할 수 있는 기능입니다.이는 시퀀싱 기술, 생물정보학 및 기계학습(생물정보학에서의 기계학습) 분야의 발전에서 비롯된다.

높은 스루풋 데이터에 사용

마이크로어레이, 차세대 염기서열 분석기(게노믹스용) 및 질량 분석기(프로테오믹스용)와 같은 새로운 바이오메디컬 기술은 방대한 양의 데이터를 생성하며, 많은 테스트를 [18]동시에 수행할 수 있습니다.신호와 잡음을 분리하기 위해서는 생물 통계학적 방법을 사용한 신중한 분석이 필요합니다.예를 들어, 마이크로 어레이는 수천 개의 유전자를 동시에 측정하기 위해 사용될 수 있으며, 이들 중 어떤 유전자가 일반 세포와 비교하여 병든 세포에서 다른 발현을 보이는지를 결정할 수 있다.그러나 유전자의 극히 일부만이 다르게 [19]발현될 것이다.

다중 공선성은 많은 경우 높은 처리량 바이오 스태틱 설정에서 발생합니다.예측 변수 간의 높은 상호 상관성(예: 유전자 발현 수준)으로 인해, 한 예측 변수의 정보가 다른 예측 변수에 포함될 수 있다.예측 변수의 5%만이 반응 변동성의 90%를 담당할 수 있습니다.이러한 경우 치수 감소의 생물 통계학적 기법을 적용할 수 있다(예를 들어 주성분 분석을 통해).선형 또는 로지스틱 회귀 분석 및 선형 판별 분석과 같은 고전적인 통계 기법은 고차원 데이터(즉, 관측치 n의 수가 특징 또는 예측 변수 p: n < p)보다 작을 때 잘 작동하지 않는다.사실 통계 모형의 예측력은 매우 낮지만 R 값은2 상당히 높을 수 있습니다.이러한 고전적인 통계 기법(특히 최소 제곱 선형 회귀)은 저차원 데이터(즉, 관측치 수 n이 예측 변수 수 p: n >> p보다 훨씬 큰 경우)를 위해 개발되었다.고차원적인 경우, 훈련 세트가 아닌 독립 유효성 검사 세트 및 해당 유효성 검사 세트의 나머지 제곱합(RSS)과2 R을 항상 고려해야 한다.

여러 예측 변수의 정보를 하나로 묶는 것이 유용한 경우가 많습니다.예를 들어, 유전자 세트 농축 분석(GSEA)은 단일 [20]유전자가 아닌 전체(기능적으로 관련된) 유전자 세트의 섭동을 고려한다.이러한 유전자 세트는 알려진 생화학적 경로 또는 기능적으로 관련된 유전자일 수 있다.이 접근방식의 장점은 보다 견고하다는 것입니다.전체 경로가 잘못 교란되는 것보다 단일 유전자가 잘못 교란되는 것으로 밝혀질 가능성이 더 높다.또한 이 접근방식을 사용하여 (JAK-STAT 신호 경로와 같은) 생화학 경로에 대한 축적된 지식을 통합할 수 있다.

데이터베이스, 데이터 마이닝 및 생물학적 해석에 있어서의 생물 정보학의 진보

생물학적 데이터베이스의 개발은 전 세계 사용자의 접근을 보장할 수 있는 가능성을 가지고 생물학적 데이터의 저장과 관리를 가능하게 한다.PubMed와 같이 데이터를 저장하고 다른 실험이나 과학 기사를 색인화한 정보와 파일(원시 또는 처리된 파일)을 검색하는 데 유용합니다.또 다른 가능성은 원하는 용어(유전자, 단백질, 질병, 유기체 등)를 검색하여 이 검색과 관련된 모든 결과를 확인하는 것입니다.SNP(dbSNP), 유전자 특성화 및 경로(KEGG), 세포 성분, 분자 기능 및 생물학적 과정(Gene Ontology)별로 분류하는 유전자 기능의 설명(Gene Ontology)에 대한 데이터베이스가 있다.[21]특정 분자 정보를 포함하는 데이터베이스 외에도, 그것들이 유기체 또는 유기체의 그룹에 대한 정보를 저장한다는 점에서 충분한 다른 데이터베이스들이 있다.하나의 유기체만을 대상으로 하지만 그에 대한 많은 데이터를 포함하고 있는 데이터베이스의 예로는 Arabidopsis thaliana 유전자 및 분자 데이터베이스인 [22]TAIR가 있다.Phytozome은 [23]식물 게놈 12개의 어셈블리와 주석 파일을 저장하고 시각화 및 분석 도구도 포함합니다.또한, 정보 교환/공유에 있는 일부 데이터베이스 간에는 상호 연관성이 있으며, 주요 이니셔티브는 DDBJ,[25] EMBL-EBI [26][27]및 NCBI의 데이터와 관련된 국제 뉴클레오티드 배열 데이터베이스 협업(INSDC)[24]이었다.

오늘날 분자 데이터 세트의 크기와 복잡성의 증가는 기계 학습 영역에서 개발된 컴퓨터 과학 알고리즘에 의해 제공되는 강력한 통계 방법을 사용하게 한다.따라서, 데이터 마이닝과 머신 러닝은,[21] 특히 지도 및 비지도 학습, 회귀, 클러스터 검출, 관련 규칙 마이닝 등의 방법을 사용하여, 생물학적 구조로서 복잡한 데이터의 패턴을 검출할 수 있게 한다.그 중 몇 가지를 나타내자면, 자기 조직 지도와 k-평균은 클러스터 알고리즘의 예이며, 신경 네트워크 구현 및 지원 벡터 머신 모델은 일반적인 기계 학습 알고리즘의 예이다.

분자생물학자, 생물정보학자, 통계학자, 컴퓨터 과학자들 간의 협업은 계획에서 데이터 생성과 분석을 거쳐 그 [21]결과에 대한 생물학적 해석으로 끝나는 실험을 정확하게 수행하기 위해 중요하다.

계산 부하가 높은 방법 사용

한편, 현대의 컴퓨터 테크놀로지와 비교적 저렴한 컴퓨팅 자원의 등장으로 부트스트랩이나 재샘플링 방법 등 컴퓨터 집약적인 생물 통계학적 방법이 가능해졌습니다.

최근 랜덤 포레스트는 통계 분류 수행 방법으로 인기를 끌고 있다.랜덤 포레스트 기술은 의사결정 트리의 패널을 생성합니다.의사결정 트리는 수학과 통계학을 기본적으로 이해하더라도 사용자가 이를 그려 해석할 수 있다는 장점이 있습니다.따라서 랜덤 포레스트는 임상 의사결정 지원 [citation needed]시스템에 사용되어 왔다.

적용들

공중 보건

공중위생(역학, 의료서비스 연구, 영양, 환경보건 및 의료정책 및 관리 등)이러한 의약품 내용에서는 임상시험의 설계와 분석을 고려하는 것이 중요합니다.하나의 예로서 환자의 중증도 상태에 대한 평가와 질병 결과의 예후가 있다.

새로운 테크놀로지와 유전학 지식을 통해 바이오 통계학은 보다 개인화된 의학으로 구성된 시스템 의학에도 사용되고 있습니다.이를 위해 기존의 환자 데이터, 임상병리학적 파라미터, 분자 및 유전자 데이터뿐만 아니라 추가 신오믹스 [28]기술에 의해 생성된 데이터 등 다양한 소스의 데이터를 통합한다.

양적 유전학

유전자형의 변화와 표현형의 변화를 연결하기 위한 집단 유전학과 통계 유전학의 연구.즉, 다유전자 제어 하에 있는 측정 가능한 특성, 양적 성질의 유전적 기초를 발견하는 것이 바람직하다.연속적인 형질을 담당하는 게놈 영역을 정량적 형질 궤적(QTL)이라고 한다.QTL의 연구는 분자 마커를 사용하고 모집단의 특성을 측정함으로써 실현 가능하지만, 이들의 매핑은 F2 또는 RIL과 같은 실험적인 교잡으로부터 모집단을 획득해야 한다.게놈에서 QTL 영역을 스캔하기 위해서는 연계에 기초한 유전자 지도를 작성해야 한다.가장 잘 알려진 QTL 매핑알고리즘에는 Interval Mapping, Composite Interval Mapping 및 Multiple Interval [29]Mapping이 있습니다.

그러나 재조합 측정량에 의해 QTL 매핑 분해능이 저하되어 큰 자손을 얻기 어려운 종의 문제가 된다.게다가 대립 유전자의 다양성은 대조적인 부모로부터 유래한 개인들로 제한되는데, 이것은 우리가 자연 [30]집단을 대표하는 개인들의 패널을 가지고 있을 때 대립 유전자의 다양성에 대한 연구를 제한한다.이러한 이유로, 특징과 분자 마커 사이의 비랜덤 연관성인 연결불균형에 기초한 QTL을 식별하기 위해 게놈 전체 연관성 연구가 제안되었다.그것은 높은 처리량 SNP [31]유전자형식의 개발에 이용되었다.

동식물 육종에서는 주로 분자 육종을 목적으로 하는 선택에서 마커를 사용하는 것이 마커 보조 선택 개발에 협력했다.QTL 매핑은 분해능에 의해 제한되지만 환경에 의해 영향을 받는 작은 효과의 드문 변종에서는 GWAS에 충분한 전력이 공급되지 않습니다.따라서 선택에서 모든 분자 마커를 사용하고 이 선택에서 후보자의 성능을 예측하기 위해 게놈 선택(GS)의 개념이 발생합니다.이 제안은 훈련 모집단을 유전자형으로 표현하고 유전자형에 속하는 개체의 게놈 추정 번식치(GEBVs)를 얻을 수 있는 모델을 개발하되 테스트 [32]모집단이라고 불리는 표현형 모집단을 얻을 수는 없다는 것이다.이러한 종류의 연구는 또한 검증 집단을 포함할 수 있으며 교차 검증의 개념으로 생각할 수 있다. 교차 검증에서는 이 집단에서 측정된 실제 표현형 결과가 예측에 기초한 표현형 결과와 비교되며, 이는 모델의 정확성을 확인하는 데 사용되었다.

요약하자면, 양적 유전학의 적용에 관한 몇 가지 요점은 다음과 같다.

  • 이것은 농작물(식물 사육)과 가축(동물 사육)을 개선하기 위해 농업에서 사용되어 왔다.
  • 생물의학 연구에서, 이 연구는 인간 유전학에서 질병에 대한 소인을 유발하거나 영향을 줄 수 있는 후보 유전자 대립 유전자를 찾는 데 도움을 줄 수 있다.

식 데이터

RT-qPCR 및 마이크로어레이와 같이 RNA-Seq 데이터와 유전자의 차이 발현에 대한 연구는 조건의 비교를 요구한다.목표는 다른 조건들 사이에서 유의미한 풍부함 변화를 가진 유전자를 식별하는 것이다.그런 다음 필요한 경우 각 조건/처리, 랜덤화 및 블럭화에 대해 반복실험을 사용하여 적절하게 설계를 수행합니다.RNA-Seq에서, 발현 정량화는 유전자 배열의 일부인 엑손으로서, 어떤 유전자 단위로 요약된 매핑된 판독의 정보를 사용합니다.마이크로 어레이 결과는 정규 분포로 근사할 수 있으므로 RNA-Seq 카운트 데이터는 다른 분포로 더 잘 설명됩니다.가장 먼저 사용된 분포는 포아송 분포였지만 표본 오차를 과소평가하여 잘못된 양성으로 이어졌습니다.현재 생물학적 변동은 음의 이항 분포의 분산 모수를 추정하는 방법에 의해 고려됩니다.일반화된 선형 모델은 통계적 유의성 테스트를 수행하기 위해 사용되며 유전자 수가 많으므로 여러 테스트 보정을 [33]고려해야 합니다.유전체학 데이터에 대한 다른 분석의 예는 마이크로 어레이 또는 프로테오믹스 [34][35]실험으로부터 나온 것이다.질병이나 질병 단계에 [36]관한 경우가 많습니다.

기타 스터디

도구들

생물학적 데이터의 통계 분석을 위해 사용할 수 있는 많은 도구가 있습니다.이들 대부분은 수많은 응용 프로그램(알파벳순)을 망라하는 기타 지식 분야에서 유용합니다.그 중 몇 가지는 다음과 같습니다.

  • ASReml: VSNi가[39] 개발한 다른 소프트웨어로 R 환경에서도 패키지로 사용할 수 있습니다.REML(제한된 최대우도)을 사용하여 일반 선형 혼합 모형에서 분산 성분을 추정하기 위해 개발되었습니다.고정 효과 및 랜덤 효과와 내포되거나 교차된 모형이 허용됩니다.서로 다른 분산-공분산 행렬 구조를 조사할 수 있습니다.
  • CycDesigN:[40] VSNi가[39] 개발한 컴퓨터 패키지입니다.CycDesigN이 취급하는 3가지 클래스 중 하나에 존재하는 설계에서 나오는 데이터를 분석하거나 실험 설계를 만들 수 있습니다.이러한 클래스는 해결 가능한 설계, 해결 불가능한 설계, 부분적으로 복제되는 설계 및 교차 설계입니다.여기에는 t-라틴화 [41]설계로서 덜 사용되는 라틴화 설계가 포함됩니다.
  • 주황색: 고급 데이터 처리, 데이터 마이닝 및 데이터 시각화를 위한 프로그래밍 인터페이스입니다.유전자 발현과 유전체학을 [21]위한 도구를 포함한다.
  • R: 통계 컴퓨팅 및 그래픽스 전용 오픈 소스 환경과 프로그래밍 언어.CRAN이 [42]관리하는 S언어 구현입니다.데이터 테이블 읽기, 기술 통계 수집, 모델 개발 및 평가 기능 외에도 전 세계 연구진이 개발한 패키지가 포함되어 있습니다.이를 통해 특정 애플리케이션에서 발생하는 [43]데이터의 통계 분석을 처리하기 위해 작성된 함수를 개발할 수 있습니다.예를 들어 생물정보학의 경우, 주요 저장소(CRAN)와 바이오컨덕터(Bioconductor)에 패키지가 있다.또한 호스팅 서비스에서 공유되는 개발 중인 패키지를 GitHub으로 사용할 수도 있습니다.
  • SAS: 대학, 서비스 및 업계에 널리 사용되는 데이터 분석 소프트웨어입니다.같은 이름의 회사(SAS Institute)가 개발한 이 프로그램은 프로그래밍에 SAS 언어를 사용합니다.
  • PLA 3.0:[44] 정량적 반응 측정(병렬-라인, 병렬-물리학, 기울기-비) 및 이분법적 측정(양적 반응, 이진 분석)을 지원하는 규제 환경(예: 약물 테스트)용 생물 통계 분석 소프트웨어이다.또한 조합 계산 및 독립 검사 데이터의 자동 데이터 집계에 대한 가중치 부여 방법을 지원합니다.
  • Weka: 시각화, 클러스터링, 회귀, 연관 규칙 및 분류를 위한 도구와 방법을 포함하는 기계 학습 및 데이터 마이닝용 Java 소프트웨어입니다.교차 검증, 부트스트래핑 및 알고리즘 비교 모듈이 있습니다.Weka는 Perl 또는 [21]R과 같은 다른 프로그래밍 언어에서도 실행할 수 있습니다.

범위 및 트레이닝 프로그램

생물 통계학의 거의 모든 교육 프로그램은 대학원 수준이다.의료, 임업 또는 농업대학에 소속된 공중보건대학원 또는 통계학과에서 주로 볼 수 있다.

여러 대학이 전담 생물 통계학과를 두고 있는 미국에서는 다른 상위권 대학들이 생물 통계학과를 통계학과 또는 역학 등의 다른 부서에 통합하고 있습니다.따라서 "생물통계학"이라는 이름을 가진 부서는 상당히 다른 구조 아래 존재할 수 있습니다.예를 들어, 비교적 새로운 생물 통계학과가 생물 정보학과 컴퓨터 생물학에 중점을 두고 설립된 반면, 전형적으로 공중 보건 학교에 소속된 오래된 학과들은 생물 정보학뿐만 아니라 역학 연구와 임상 시험을 포함하는 더 전통적인 연구 라인을 갖게 될 것이다.통계학과 생물통계학과가 모두 존재하는 전 세계 대형 대학에서는 두 학과 간의 통합 정도는 최소한의 협업에서 매우 긴밀한 협업까지 다양할 수 있습니다.일반적으로, 통계 프로그램과 생물 통계 프로그램의 차이는 두 가지이다. (i) 통계 부서는 종종 생물 통계 프로그램에서 덜 흔한 이론/방법학적 연구를 주최하고, (ii) 통계 부서는 생물 의학 응용 분야를 포함할 수 있는 연구 라인을 가지고 있다.ndustry(품질관리), 비즈니스 및 경제, 의학 이외의 생물학 분야.

전문지

다음 항목도 참조하십시오.생물 통계 저널 목록
  • 생물[45] 통계학
  • 국제 생물 통계[46] 저널
  • 역학 및 생물통계학[47] 저널
  • 생물 통계와 공중[48] 보건
  • 바이오메트릭스[49]
  • 바이오메트리카[50]
  • 바이오메트릭[51] 저널
  • 생물측정학 및 작물학[52] 통신
  • 유전학과 분자생물학에서의[53] 통계적 응용
  • 의료[54] 연구의 통계적 방법
  • 의약품 통계[55]
  • 의료 통계[56]

「 」를 참조해 주세요.

레퍼런스

  1. ^ Gunter, Chris (10 December 2008). "Quantitative Genetics". Nature. 456 (7223): 719. Bibcode:2008Natur.456..719G. doi:10.1038/456719a. PMID 19079046.
  2. ^ Charles T. Munger (2003-10-03). "Academic Economics: Strengths and Faults After Considering Interdisciplinary Needs" (PDF).
  3. ^ a b c Nizamuddin, Sarah L.; Nizamuddin, Junaid; Mueller, Ariel; Ramakrishna, Harish; Shahul, Sajid S. (October 2017). "Developing a Hypothesis and Statistical Planning". Journal of Cardiothoracic and Vascular Anesthesia. 31 (5): 1878–1882. doi:10.1053/j.jvca.2017.04.020. PMID 28778775.
  4. ^ a b c d Overholser, Brian R; Sowinski, Kevin M (2017). "Biostatistics Primer: Part I". Nutrition in Clinical Practice. 22 (6): 629–35. doi:10.1177/0115426507022006629. PMID 18042950.
  5. ^ Szczech, Lynda Anne; Coladonato, Joseph A.; Owen, William F. (4 October 2002). "Key Concepts in Biostatistics: Using Statistics to Answer the Question "Is There a Difference?"". Seminars in Dialysis. 15 (5): 347–351. doi:10.1046/j.1525-139X.2002.00085.x. PMID 12358639. S2CID 30875225.
  6. ^ Sandelowski, Margarete (2000). "Combining Qualitative and Quantitative Sampling, Data Collection, and Analysis Techniques in Mixed-Method Studies". Research in Nursing & Health. 23 (3): 246–255. CiteSeerX 10.1.1.472.7825. doi:10.1002/1098-240X(200006)23:3<246::AID-NUR9>3.0.CO;2-H. PMID 10871540.
  7. ^ Maths, Sangaku. "Absolute, relative, cumulative frequency and statistical tables – Probability and Statistics". www.sangakoo.com. Retrieved 2018-04-10.
  8. ^ a b "DATASUS: TabNet Win32 3.0: Nascidos vivos – Brasil". DATASUS: Tecnologia da Informação a Serviço do SUS.
  9. ^ a b c d Forthofer, Ronald N.; Lee, Eun Sul (1995). Introduction to Biostatistics. A Guide to Design, Analysis, and Discovery. Academic Press. ISBN 978-0-12-262270-0.
  10. ^ Pearson, Karl (1895-01-01). "X. Contributions to the mathematical theory of evolution.—II. Skew variation in homogeneous material". Phil. Trans. R. Soc. Lond. A. 186: 343–414. Bibcode:1895RSPTA.186..343P. doi:10.1098/rsta.1895.0010. ISSN 0264-3820.
  11. ^ Utts, Jessica M. (2005). Seeing through statistics (3rd ed.). Belmont, CA: Thomson, Brooks/Cole. ISBN 978-0534394028. OCLC 56568530.
  12. ^ Jarrell, Stephen B. (1994). Basic statistics. Dubuque, Iowa: Wm. C. Brown Pub. ISBN 978-0697215956. OCLC 30301196.
  13. ^ Gujarati, Damodar N. (2006). Econometrics. McGraw-Hill Irwin.
  14. ^ "Essentials of Biostatistics in Public Health & Essentials of Biostatistics Workbook: Statistical Computing Using Excel". Australian and New Zealand Journal of Public Health. 33 (2): 196–197. 2009. doi:10.1111/j.1753-6405.2009.00372.x. ISSN 1326-0200.
  15. ^ Baker, Monya (2016). "Statisticians issue warning over misuse of P values". Nature. 531 (7593): 151. Bibcode:2016Natur.531..151B. doi:10.1038/nature.2016.19503. PMID 26961635.
  16. ^ Benjamini, Y. & Hochberg, Y. 오검출률 제어: 여러 테스트에 대한 실용적이고 강력한 접근법왕립통계학회지시리즈 B(방법론) 57, 289–300(1995).
  17. ^ "Null hypothesis". www.statlect.com. Retrieved 2018-05-08.
  18. ^ Hayden, Erika Check (8 February 2012). "Biostatistics: Revealing analysis". Nature. 482 (7384): 263–265. doi:10.1038/nj7384-263a. PMID 22329008.
  19. ^ Efron, Bradley (February 2008). "Microarrays, Empirical Bayes and the Two-Groups Model". Statistical Science. 23 (1): 1–22. arXiv:0808.0572. doi:10.1214/07-STS236. S2CID 8417479.
  20. ^ Subramanian, A.; Tamayo, P.; Mootha, V. K.; Mukherjee, S.; Ebert, B. L.; Gillette, M. A.; Paulovich, A.; Pomeroy, S. L.; Golub, T. R.; Lander, E. S.; Mesirov, J. P. (30 September 2005). "Gene set enrichment analysis: A knowledge-based approach for interpreting genome-wide expression profiles". Proceedings of the National Academy of Sciences. 102 (43): 15545–15550. Bibcode:2005PNAS..10215545S. doi:10.1073/pnas.0506580102. PMC 1239896. PMID 16199517.
  21. ^ a b c d e Moore, Jason H (2007). "Bioinformatics". Journal of Cellular Physiology. 213 (2): 365–9. doi:10.1002/jcp.21218. PMID 17654500. S2CID 221831488.
  22. ^ "TAIR - Home Page". www.arabidopsis.org.
  23. ^ "Phytozome". phytozome.jgi.doe.gov.
  24. ^ "International Nucleotide Sequence Database Collaboration - INSDC". www.insdc.org.
  25. ^ "Top". www.ddbj.nig.ac.jp.
  26. ^ "The European Bioinformatics Institute < EMBL-EBI". www.ebi.ac.uk.
  27. ^ "National Center for Biotechnology Information". www.ncbi.nlm.nih.gov. U. S. National Library of Medicine –.
  28. ^ Apweiler, Rolf; et al. (2018). "Whither systems medicine?". Experimental & Molecular Medicine. 50 (3): e453. doi:10.1038/emm.2017.290. PMC 5898894. PMID 29497170.
  29. ^ Zeng, Zhao-Bang (2005). "QTL mapping and the genetic basis of adaptation: Recent developments". Genetica. 123 (1–2): 25–37. doi:10.1007/s10709-004-2705-0. PMID 15881678. S2CID 1094152.
  30. ^ Korte, Arthur; Farlow, Ashley (2013). "The advantages and limitations of trait analysis with GWAS: A review". Plant Methods. 9: 29. doi:10.1186/1746-4811-9-29. PMC 3750305. PMID 23876160.
  31. ^ Zhu, Chengsong; Gore, Michael; Buckler, Edward S; Yu, Jianming (2008). "Status and Prospects of Association Mapping in Plants". The Plant Genome. 1: 5–20. doi:10.3835/plantgenome2008.02.0089.
  32. ^ Crossa, José; Pérez-Rodríguez, Paulino; Cuevas, Jaime; Montesinos-López, Osval; Jarquín, Diego; De Los Campos, Gustavo; Burgueño, Juan; González-Camacho, Juan M; Pérez-Elizalde, Sergio; Beyene, Yoseph; Dreisigacker, Susanne; Singh, Ravi; Zhang, Xuecai; Gowda, Manje; Roorkiwal, Manish; Rutkoski, Jessica; Varshney, Rajeev K (2017). "Genomic Selection in Plant Breeding: Methods, Models, and Perspectives" (PDF). Trends in Plant Science. 22 (11): 961–975. doi:10.1016/j.tplants.2017.08.011. PMID 28965742.
  33. ^ Oshlack, Alicia; Robinson, Mark D; Young, Matthew D (2010). "From RNA-seq reads to differential expression results". Genome Biology. 11 (12): 220. doi:10.1186/gb-2010-11-12-220. PMC 3046478. PMID 21176179.
  34. ^ Helen Causton; John Quackenbush; Alvis Brazma (2003). Statistical Analysis of Gene Expression Microarray Data. Wiley-Blackwell.
  35. ^ Terry Speed (2003). Microarray Gene Expression Data Analysis: A Beginner's Guide. Chapman & Hall/CRC.
  36. ^ Frank Emmert-Streib; Matthias Dehmer (2010). Medical Biostatistics for Complex Diseases. Wiley-Blackwell. ISBN 978-3-527-32585-6.
  37. ^ Warren J. Ewens; Gregory R. Grant (2004). Statistical Methods in Bioinformatics: An Introduction. Springer.
  38. ^ Matthias Dehmer; Frank Emmert-Streib; Armin Graber; Armindo Salvador (2011). Applied Statistics for Network Biology: Methods in Systems Biology. Wiley-Blackwell. ISBN 978-3-527-32750-8.
  39. ^ a b "Home - VSN International". www.vsni.co.uk.
  40. ^ "CycDesigN - VSN International". www.vsni.co.uk.
  41. ^ Piepho, Hans-Peter; Williams, Emlyn R; Michel, Volker (2015). "Beyond Latin Squares: A Brief Tour of Row-Column Designs". Agronomy Journal. 107 (6): 2263. doi:10.2134/agronj15.0144.
  42. ^ "The Comprehensive R Archive Network". cran.r-project.org.
  43. ^ Renganathan V (2021). Biostatistics explored through R software: An overview. ISBN 9789354936586.
  44. ^ Stegmann, Dr Ralf (2019-07-01). "PLA 3.0". PLA 3.0 – Software for Biostatistical Analysis. Retrieved 2019-07-02.
  45. ^ "Biostatistics - Oxford Academic". OUP Academic.
  46. ^ "The International Journal of Biostatistics".
  47. ^ "PubMed Journals will be shut down". 15 June 2018.
  48. ^ https://ebph.it/ 역학
  49. ^ "Biometrics". onlinelibrary.wiley.com. doi:10.1111/(ISSN)1541-0420.
  50. ^ "Biometrika - Oxford Academic". OUP Academic.
  51. ^ "Biometrical Journal". onlinelibrary.wiley.com. doi:10.1002/(ISSN)1521-4036.
  52. ^ "Communications in Biometry and Crop Science". agrobiol.sggw.waw.pl.
  53. ^ "Statistical Applications in Genetics and Molecular Biology". www.degruyter.com. 1 May 2002.
  54. ^ "Statistical Methods in Medical Research". SAGE Journals.
  55. ^ "Pharmaceutical Statistics". onlinelibrary.wiley.com.
  56. ^ "Statistics in Medicine". onlinelibrary.wiley.com. doi:10.1002/(ISSN)1097-0258.

외부 링크

Wikimedia Commons 생물 통계 관련 미디어