밀도 추정

Density estimation
신호 처리 개념은 스펙트럼 밀도 추정을 참조하십시오.
커널 밀도 추정을 사용한 밀도 추정 시연:실제 밀도는 0과 3을 중심으로 한 두 개의 가우시안 혼합으로, 파란색 실선으로 표시됩니다.각 프레임에서 100개의 샘플이 빨간색으로 표시된 분포에서 생성됩니다.각 샘플의 중앙에 가우스 커널이 회색으로 그려집니다.가우시안 평균은 파선된 검은색 곡선에 표시된 밀도 추정치를 산출합니다.

확률과 통계학에서 밀도 추정은 관측할 수 없는 기본 확률 밀도 함수의 관측 데이터에 기초한 추정의 구성이다.관측 불가능한 밀도 함수는 많은 모집단이 분포하는 밀도로 간주되며, 데이터는 일반적으로 해당 모집단에서 무작위로 추출된 표본으로 간주됩니다.

Parzen 창과 벡터 양자화를 포함한 다양한 데이터 클러스터링 기술을 포함하여 밀도 추정에 대한 다양한 접근법이 사용됩니다.밀도 추정의 가장 기본적인 형태는 크기 조정된 히스토그램입니다.

밀도 추정 예제

p(glu 당뇨병=1) (빨간색), p(glu 당뇨병=0) (파란색) 및 p(glu)(검은색)의 추정 밀도
p(θ=1 glu)의 추정 확률
p의 추정 확률(θ=1 glu)

당뇨병 발생 기록을 검토하겠습니다.데이터 세트 설명에서 인용한 내용은 다음과 같습니다.

세계보건기구(WHO) 기준에 따라 애리조나주 피닉스 인근에 사는 피마 인디언 혈통인 21세 이상의 여성 인구가 당뇨병 검사를 받았다.이 데이터는 미국 국립당뇨병 및 소화기 및 신장질환 연구소에 의해 수집되었다.532개의 완전한 [1][2]기록을 사용했습니다.

이 예에서 우리는 "glu"(플라즈마 포도당 농도)에 대한 세 가지 밀도 추정치를 구축한다. 하나는 당뇨병의 존재에 대한 조건, 두 번째는 당뇨병의 부재에 대한 조건, 세 번째는 당뇨병에 대한 조건이다.그런 다음 조건부 밀도 추정치를 사용하여 "glu"에 조건부 당뇨병의 확률을 구성합니다.

"glu" 데이터는 R 프로그래밍 언어의 MASS[3] 패키지에서 얻었습니다.R 내에서?Pima.tr그리고.?Pima.te그 자료를 자세히 설명하다

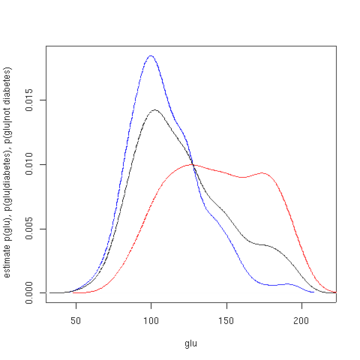
당뇨병 환자의 글루 평균은 143.1이고 표준 편차는 31.26이다.비당뇨병 사례에서 글루의 평균은 110.0이고 표준 편차는 24.29입니다.이를 통해 이 데이터 집합에서 당뇨병 환자는 더 높은 수준의 "glu"와 관련이 있음을 알 수 있습니다.이것은 추정 밀도 함수의 플롯을 통해 더 명확해질 것이다.

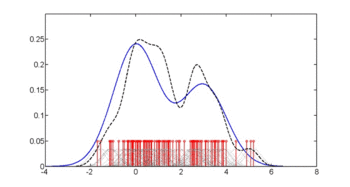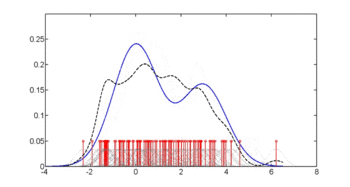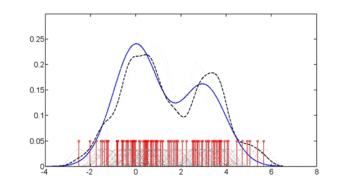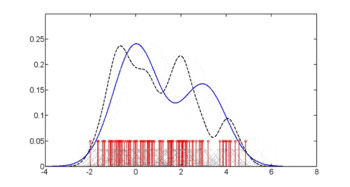
첫 번째 그림은 p(glu 당뇨병=1), p(glu 당뇨병=0) 및 p(glu)의 밀도 추정치를 보여준다.밀도 추정치는 가우스 커널을 사용한 커널 밀도 추정치입니다.즉, 각 데이터 지점에 가우스 밀도 함수를 배치하고 데이터 범위에 걸쳐 밀도 함수의 합계가 계산됩니다.

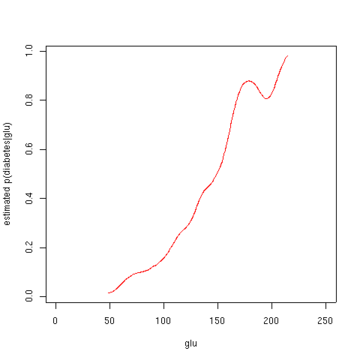
당뇨병을 조건으로 하는 글루 농도에서 베이즈의 법칙을 통해 글루를 조건으로 하는 당뇨병 확률을 얻을 수 있다.간결하게 하기 위해 이 공식에서 "당뇨병"은 "db"로 약칭됩니다.

두 번째 그림은 추정 후확률 p(glu=1 glu)이다.이러한 데이터를 통해 글루 수치가 증가하는 것은 당뇨병과 관련이 있는 것으로 보인다.

예를 들어 스크립트

다음 R 명령은 위에 표시된 그림을 만듭니다.이러한 명령어는 명령 프롬프트에서 컷 앤 페이스트를 사용하여 입력할 수 있습니다. 

도서관(덩어리) 데이터.(Pima.tr) 데이터.(피마테)  피마 <-> rbind(Pima.tr, 피마테) 글루  <-> 피마[, '글']  d0 <-> 피마[, '타입'] == '아니요' d1 <-> 피마[, '타입'] == '네' base.rate.d1 <-> 합(d1) / (합(d1) + 합(d0))  밀도    <-> 밀도(글루) glu.d0. 밀도 <-> 밀도(글루[d0]) glu.d1. 밀도 <-> 밀도(글루[d1])  glu.d0.f <-> 약재미(glu.d0. 밀도$x, glu.d0. 밀도$y) glu.d1.f <-> 약재미(glu.d1. 밀도$x, glu.d1. 밀도$y)  p.d.given.glu <-> 기능.(글루, base.rate.d1) {     p1 <-> glu.d1.f(글루) * base.rate.d1     p0 <-> glu.d0.f(글루) * (1 - base.rate.d1)     p1 / (p0 + p1) }  x <-> 1:250 y <-> p.d.given.glu(x, base.rate.d1) 줄거리.(x, y, 유형='l', 콜='빨간색', xlab='글', 랩='crypto p(crypto glu)')  줄거리.(밀도(글루[d0]), 콜='파랑', xlab='글', 랩=p(glu), p(당뇨병), p(당뇨병이 아닌 glu)', 주된=NA) 줄들(밀도(글루[d1]), 콜='빨간색')

위의 조건부 밀도 추정기는 무조건 밀도에 최적인 대역폭을 사용합니다.또는 Hall, Racine, Li(2004)[4] 및 Rnp[5] 패키지의 방법을 사용하여 조건부 밀도 추정에 최적인 자동(데이터 중심) 대역폭을 선택할 수 있습니다.np 패키지의 개요에 대해서는 np vignette를[6] 참조해 주세요.다음 R 명령에서는npcdens()최적의 평활 기능을 제공합니다."예"/"아니오"라는 응답이 요인입니다. 

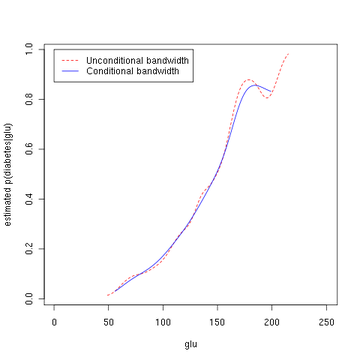
도서관(np)  회계연도 x의 <-> npcdens(유형~글루, nmulti=1, 데이터.=피마)  Pima.eval <-> data.frame(데이터 프레임)(유형=인자("네"),                         글루=인식하다(분(피마$글루), 맥스.(피마$글루), 길이=250))   줄거리.(x, y, 유형='l', lty=2, 콜='빨간색', xlab='글',      랩='crypto p(crypto glu)') 줄들(Pima.eval$글루, 예측하다(회계연도 x의, 새로운 데이터=Pima.eval), 콜='파랑') 범례(0, 1, c("무조건 대역폭", "조건부 대역폭"),        콜=c("빨간색", '파랑'), lty=c(2, 1))

세 번째 그림에서는 Hall, Racine 및[4] Li 방법을 통해 최적의 평활을 사용하고 있습니다.이는 위의 두 번째 그림에서 사용되는 무조건 밀도 대역폭이 다소 부족할 수 있는 조건부 밀도 추정치를 산출하고 있음을 나타냅니다.

응용 프로그램 및 목적

밀도 추정치의 매우 자연스러운 사용은 주어진 데이터 집합의 속성에 대한 비공식적인 조사이다.밀도 추정치는 데이터의 왜도 및 다중 모드성 등의 특징을 나타내는 귀중한 지표가 될 수 있습니다.경우에 따라서는 자명한 사실로 간주될 수 있는 결론을 도출하는 반면, 다른 경우에는 추가 분석 및/[7]또는 데이터 수집을 지시하는 것만을 수행하게 된다.

Gumbel 분포에 대한 히스토그램 및 밀도 함수

통계의 중요한 측면은 종종 다른 방법으로 얻었을 수 있는 결론에 대한 설명과 설명을 제공하기 위해 고객에게 데이터를 다시 제시하는 것이다.밀도 추정치는 수학자가 아닌 사람이 이해하기 쉽다는 단순한 이유로 이러한 목적에 이상적입니다.

이변량 [9]데이터의 중요한 경우를 포함하여 탐색적 및 제시적 목적을 위한 밀도 추정치의 사용을 보여주는 더 많은 예.

밀도 추정은 이상 검출 또는 신규 [10]검출에도 자주 사용됩니다.관찰이 매우 저밀도 영역에 있는 경우 이상 또는 신규일 가능성이 높습니다.

  • 수문학에서는 확률 분포로 분석되는 강우 및 하천 유량 데이터의 히스토그램과 추정 밀도 함수를 사용하여 발생 [11]빈도와 행동을 파악한다.파란색 그림에 예가 나와 있습니다.

「 」를 참조해 주세요.

레퍼런스

  1. ^ "Diabetes in Pima Indian Women - R documentation".
  2. ^ Smith, J. W., Everhart, J. E., Dickson, W. C., Knowler, W. C. and Johannes, R. S. (1988). R. A. Greenes (ed.). "Using the ADAP learning algorithm to forecast the onset of diabetes mellitus". Proceedings of the Symposium on Computer Applications in Medical Care (Washington, 1988). Los Alamitos, CA: 261–265. PMC 2245318.{{cite journal}}: CS1 maint: 여러 이름: 작성자 목록(링크)
  3. ^ "Support Functions and Datasets for Venables and Ripley's MASS".
  4. ^ a b Peter Hall; Jeffrey S. Racine; Qi Li (2004). "Cross-Validation and the Estimation of Conditional Probability Densities". Journal of the American Statistical Association. 99 (468): 1015–1026. CiteSeerX 10.1.1.217.93. doi:10.1198/016214504000000548. S2CID 5945686.
  5. ^ "The np package - An R package that provides a variety of nonparametric and semiparametric kernel methods that seamlessly handle a mix of continuous, unordered, and ordered factor data types".
  6. ^ Tristen Hayfield; Jeffrey S. Racine. "The np Package" (PDF).
  7. ^ Silverman, B. W. (1986). Density Estimation for Statistics and Data Analysis. Chapman and Hall. ISBN 978-0412246203.
  8. ^ 확률 분포 및 밀도 함수를 위한 계산기
  9. ^ Geof H., Givens(2013).계산 통계 정보.와일리, 페이지 330ISBN 978-0-470-53331-4.
  10. ^ Pimentel, Marco A.F.; Clifton, David A.; Clifton, Lei; Tarassenko, Lionel (2 January 2014). "A review of novelty detection". Signal Processing. 99 (June 2014): 215–249. doi:10.1016/j.sigpro.2013.12.026.
  11. ^ 히스토그램 및 확률 밀도 함수의 그림

원천

외부 링크