파이 차트

Pie chart
원 그래프와 혼동하지 마십시오.
Wikipedia에서 원형 차트 생성에 대한 내용은 Wikipedia:그래프 및 차트 및 템플릿:파이 차트
영어 원어민 인구 원 그래프

원형 차트(또는 원형 차트)는 원형 통계 그래픽으로, 숫자 비율을 나타내기 위해 슬라이스로 나뉩니다.원형 차트에서 각 슬라이스의 호 길이(그리고 중앙 각도와 면적)는 해당 슬라이스가 나타내는 양에 비례합니다.얇게 썬 파이와 닮았다고 해서 이름이 붙여졌지만, 그것을 보여주는 방법에는 여러 가지 종류가 있다.가장 먼저 알려진 파이 차트는 일반적으로 윌리엄 플레이페어의 1801년 [1][2]통계 요약본으로 알려져 있다.

파이 차트는 비즈니스 세계와 대중 [3]매체에서 매우 널리 사용되고 있습니다.그러나 이러한 데이터는 비판을 [4]받고 있으며, 많은 전문가들은 특정 원형 차트의 다른 섹션을 비교하거나 다른 원형 차트의 데이터를 비교하는 것이 어렵다는 연구 결과가 나왔기 때문에 [5][6][7][8]이를 피하는 것이 좋습니다.대부분의 경우 원형 차트는 막대 차트, 상자 그림, 점 그림 등과 같은 다른 그래프로 대체할 수 있습니다.

역사

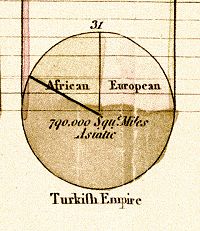
가장 먼저 알려진 파이 차트는 일반적으로 William Playfair의 1801년 통계 개요에 기인하며, 두 개의 그래프가 사용된다.[1][2][9]Playfair는 일련의 파이 차트를 포함한 일러스트를 제시했다.이 차트들 중 하나는 1789년 이전에 아시아, 유럽, 아프리카에 있었던 터키 제국의 비율을 나타낸 것이다.이 발명품은 [1]처음에는 널리 사용되지 않았다.

Playfair는 추가 [10]정보를 추가하기 위해 파이 차트가 3차원이 필요하다고 생각했습니다.

플로렌스 나이팅게일이 파이 차트를 발명하지는 않았을지 모르지만, 그녀는 그것을 좀 더 읽기 쉽게 하기 위해 수정했고, 그것이 오늘날에도 널리 쓰이게 되었다.실제로 나이팅게일은 쐐기의 너비 대신 길이를 가변적으로 바꾸도록 파이 차트를 재구성했다.그래프는 수탉의 [11]빗과 비슷했다.그녀는 나중에 플레이페어의 [12]창작물이 무명하고 실용성이 부족하기 때문에 그것을 만든 것으로 추정되었다.나이팅게일의 극지방 diagram,[13]:107이나 가끔은 나이팅게일은 증가했다 도표, 현대식 원형 히스토그램에, 환자 사망률의 그녀는 가까스로 군대 야전 병원에서 계절적인 소식통을 보여 주기 위해 등가, 노트에 문제 보건·효율 작동에 영향을 미치는, 그리고 병원 행정부는 영국, s출판되었다취에 멤머는1858년 에엔 빅토리아.역사학자 휴 스몰에 따르면, "그녀는 사람들에게 [11]변화의 필요성을 설득하기 위해 [파이 차트]를 처음으로 사용했을지도 모른다."

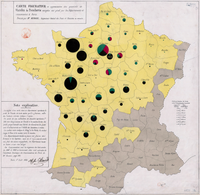
1858년 프랑스 엔지니어 찰스 조셉 미나드도 파이 차트를 사용했다.1858년 그의 지도는 파리에서 소비하기 위해 프랑스 전역에서 보내진 소들을 나타내기 위해 파이 차트를 사용했다.

19세기 초기 원형 차트
  • Pie charts from William Playfair's "Statistical Breviary", 1801

    William Playfair의 "Statistical Breviary", 1801년 원 그래프

  • One of the pie charts, 1801

    파이 차트 중 하나인 1801년

  • Minard's map, 1858

    미나드 지도, 1858년

  • Polar chart by Florence Nightingale, 1858

    플로렌스 나이팅게일의 극지도, 1858년

변종 및 유사 차트

3D 파이 차트 및 투시 파이 케이크

3D 원형 차트 또는 투시 원형 차트는 차트를 3D로 표시하는 데 사용됩니다.심미적인 이유로 자주 사용되는 3차원은 데이터 판독을 개선하지 않는다. 반대로, 이러한 플롯은 3차원과 관련된 원근법의 왜곡된 효과 때문에 해석하기 어렵다.관심 데이터를 표시하는 데 사용되지 않는 불필요한 치수는 원형 [7][14]차트뿐만 아니라 차트 전반에 사용하지 않는 것이 좋습니다.

도넛 차트

도넛 차트 중앙에 있는 구멍 형태의 데이터에 대한 정보

도넛 차트(도넛이라고도 함)는 파이 차트의 변형으로, 데이터 전체에 대한 추가 정보를 포함할 수 있는 빈 가운데가 있습니다.[15][16] 도넛 차트는 [citation needed]비율을 설명하는 데 목적이 있다는 점에서 파이 차트와 유사합니다.이 유형의 원형 그래프는 한 번에 여러 통계를 지원할 수 있으며 표준 원형 [16]차트에 비해 더 나은 데이터 강도 비율을 제공합니다.중앙에 정보를 포함할 필요는 없습니다.

분해된 원형 차트

예제 데이터의 분해 원형 차트(아래 참조)와 최대 파티 그룹이 분해되었습니다.

디스크의 나머지 부분과 하나 이상의 섹터가 분리된 차트를 분해 원형 차트라고 합니다.이 효과는 섹터를 강조 표시하거나 차트의 작은 세그먼트를 작은 비율로 강조 표시하는 데 사용됩니다.

극지방도

플로렌스 나이팅게일의 "동부군 사망원인 그림"

극 영역 다이어그램은 섹터가 동일한 각도를 가지며 각 섹터가 원의 중심에서 연장되는 거리가 다르다는 점을 제외하고는 일반적인 원형 차트와 유사합니다.극지역 다이어그램은 주기적 현상(예: 월별 사망자 수)을 플롯하는 데 사용된다.예를 들어, 한 해 동안 매월 사망자 수를 플롯할 경우, 각각 30도의 동일한 각도를 가진 12개의 섹터(월 1개)가 있을 것이다.각 부문의 반지름은 해당 달의 사망률의 제곱근에 비례하므로, 한 부문의 면적은 한 달 동안의 사망률을 나타냅니다.사망원인에 따라 월별 사망률을 세분화하면 플로렌스 나이팅게일이 개발한 극지 도표에서 볼 수 있듯이 하나의 도표로 여러 가지 비교를 할 수 있다.

극지방도를 최초로 사용한 것은 앙드레 미쉘 게리가 1829년 발표한 논문에서 그가 쿠르베 서큘러(원곡선)라고 불렀는데, 이는 1년 동안 풍향의 계절과 일상의 변화와 하루의 [17]시간별 출생과 사망을 보여준다.Léon Lalanne은 나중에 1843년에 나침반 주변의 풍향의 빈도를 나타내기 위해 극지도를 사용했다.풍향장미는 여전히 기상학자들에 의해 사용되고 있다.나이팅게일은 1858년에 그녀의 장미 그림을 출판했다.비록 "콕스콤"이라는 이름이 이런 유형의 다이어그램과 연관되기는 했지만, 나이팅게일은 원래 이 다이어그램이 이 특정한 유형의 [18]다이어그램이 아니라 관심을 끄는 차트 및 표의 책인 이 도표가 처음 등장한 출판물을 가리키기 위해 이 용어를 사용했다.

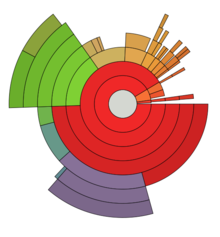
링 차트, 선버스트 차트 및 다단계 원형 차트

Linux 파일 시스템의 디스크 사용량을 나타내는 다단계 원형 차트
참고 항목: 반지름 트리

선버스트 차트 또는 다단계 원형 차트라고도 하는 링 차트는 [19]동심원으로 표시된 계층 데이터를 시각화하는 데 사용됩니다.중앙의 원은 중심에서 바깥쪽으로 이동하는 계층이 있는 루트 노드를 나타냅니다.내부 원의 세그먼트는 상위 [20]세그먼트의 각도 스위프 내에 있는 외부 원의 세그먼트와 계층 관계를 가진다.

스파이 차트

4개 학교의 학생 수와 학생 비용을 비교한 스파이 차트

극지 면적 차트의 변형은 Dror Feitelson이 [21]설계한 스피 차트입니다.이 설계에서는 두 세트의 관련 데이터를 비교할 수 있도록 수정된 극성 영역 차트에 정규 원형 차트를 겹칩니다.기준 원형 차트는 슬라이스 크기가 서로 다른 일반적인 방식으로 첫 번째 데이터 세트를 나타냅니다.두 번째 세트는 중첩된 극 영역 차트로 나타나며, 베이스와 동일한 각도를 사용하고 데이터에 맞게 반지름을 조정합니다.예를 들어, 기준 원형 차트는 모집단 내 연령 및 성별 그룹의 분포를 보여주고 도로 사상자 간의 표현을 중첩시킬 수 있습니다.특히 사고에 노출되기 쉬운 연령대와 성별 그룹은 원래 원형 차트를 벗어나는 슬라이스로 두드러집니다.

정사각형 차트 / 와플 차트

원형 차트보다 더 작은 백분율이 더 쉽게 표시되는지 보여 주는 정사각형 원형 차트(와플 차트)입니다.10x10 그리드에서 각 셀은 1%를 나타냅니다.

와플 차트라고도 불리는 정사각형 차트는 백분율을 나타내기 위해 원 대신 정사각형을 사용하는 원형 차트의 한 형태이다.기본 원형 원형 원형 차트와 마찬가지로 정사각형 원형 차트는 총 100%에서 각 백분율을 차지합니다.대부분의 경우 10x10 그리드이며, 각 셀은 1%를 나타냅니다.이름에도 불구하고 정사각형 대신 동그라미, 픽토그램(사람의 그림 등) 등을 사용할 수 있습니다.정사각형 차트의 주요 이점 중 하나는 전통적인 원형 차트에서는 보기 힘든 더 작은 비율을 [22]쉽게 나타낼 수 있다는 것입니다.

예

예제 데이터의 원형 차트

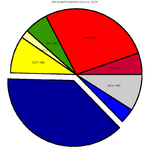
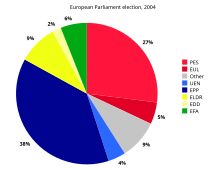
다음 예제 차트는 2004년 유럽의회 선거의 예비 결과에 기초하고 있습니다.이 표에는 각 정당 그룹에 할당된 의석 수와 각 정당 그룹이 구성하는 총 의석 수의 파생 백분율이 나와 있습니다.각 섹터의 도출된 중심 각도인 마지막 열의 값은 백분율에 360°를 곱하여 구합니다.

그룹. 좌석 백분율(%) 중심 각도(°)
에울 39 5.3 19.2
PES 200 27.3 98.4
EFA 42 5.7 20.7
EDD 15 2.0 7.4
엘도 67 9.2 33.0
EPP 276 37.7 135.7
전원 27 3.7 13.3
다른. 66 9.0 32.5
총 732 99.9* 360.2*

※ 반올림 때문에 합계가 100과 360이 되지 않습니다.

각 중심 각도의 크기는 해당 수량(여기서는 시트 수)의 크기에 비례합니다.중심 각도의 합계는 360°여야 하므로, 총량 Q에 해당하는 양의 중심 각도는 360Q도이다.이 예에서 가장 큰 그룹(European People's Party(EPP))의 중심 각도는 135.7°입니다. 소수점 한 자리로 반올림한 0.377 곱하기 360은 135.7과 같기 때문입니다.

사용법과 효과

대기 성분 백분율을 보여주는 3D 원형 차트

원형 차트에서 나타나는 결함은 시각적 인코딩("슬라이스")을 나타내는 데이터(일반적으로 백분율)에서 분리하지 않고는 몇 개 이상의 값을 표시할 수 없다는 것입니다.슬라이스가 너무 작아지면 파이 차트는 색상, 텍스처 또는 화살표를 사용하여 판독자가 이해할 수 있도록 해야 합니다.따라서 대량의 데이터에 사용하기에는 적합하지 않습니다.원형 차트는 별도의 범례를 가질 필요가 없는 유연한 막대형 차트와 비교하여 페이지에서 더 많은 공간을 차지하며 평균이나 목표값과 같은 다른 값을 [7]동시에 표시할 수 있습니다.

통계학자들은 일반적으로 파이 차트를 정보를 표시하는 빈약한 방법으로 간주하며 과학 문헌에서는 흔치 않습니다.한 가지 이유는 길이가 아닌 면적을 사용할 때 차트의 항목 크기와 다른 항목을 다른 [23]모양으로 표시할 때 비교하기가 더 어렵기 때문입니다.

파이차트와 바르차트로 표시된 세 가지 백분율 집합입니다.일반적으로 바르차트의 데이터를 비교하는 것이 더 쉽습니다.

또한 AT&T Bell Laboratories에서 실시한 연구에서는 각도별 비교가 길이별 비교보다 정확도가 낮은 것으로 나타났다.대부분의 피험자는 파이 차트의 슬라이스를 크기별로 정렬하는 데 어려움을 겪습니다. 동등한 막대 차트를 사용하면 비교가 훨씬 쉽습니다.[24]마찬가지로 막대 차트를 사용하면 데이터 집합 간의 비교가 더 쉬워집니다.그러나 특정 범주(파이 조각)를 단일 차트의 전체(전체 파이)와 비교하는 것이 목표이고 배수가 25 또는 50%에 가까운 경우에는 종종 막대 [25][26]그래프보다 파이 차트가 더 효과적일 수 있습니다.

18개의 값이 있고 일부 색상이 반복되는 원형 차트 예제

단면이 많은 원형 차트에서는 여러 값이 같거나 유사한 색으로 표시될 수 있으므로 해석이 어렵습니다.

2019년 테스트 매치에서 인도 크리켓 선수들의 타격과 런 기록을 보여주는 도넛 모양의 파이 차트의 예

유럽 가시화 회의에서 발표된 여러 연구는 여러 파이 차트 [27][28][22]형식의 상대적 정확성을 분석하여 파이 차트와 도넛 차트가 읽을 때 유사한 오류 수준을 생성하고 정사각형 파이 차트가 가장 정확한 [29]판독치를 제공한다는 결론에 도달했습니다.

레퍼런스

  1. ^ a b c 스펜스(2005)
  2. ^ a b 터프테, 44페이지
  3. ^ 클리블랜드, 262페이지
  4. ^ 윌킨슨, 페이지 23
  5. ^ 터프테, 페이지 178
  6. ^ 반 벨, 페이지 160~162
  7. ^ a b c 스테판 푸"Save the Pie for Desert", 2007년 8월, 2010-02-02 취득
  8. ^ Steve Fenton "파이 차트는 나빠"
  9. ^ "Milestones in the History of Thematic Cartography, Statistical Graphics, and Data Visualization". www.datavis.ca.
  10. ^ 팔스키, 페이지 144~145
  11. ^ a b Greenbaum, Hilary; Rubinstein, Dana (20 April 2012). "Who Made That Pie Chart?". The New York Times.
  12. ^ QI에 대한 이 정보에 대한 Dave 기사
  13. ^ Cohen, I. Bernard (March 1984). "Florence Nightingale". Scientific American. 250 (3): 128–137. Bibcode:1984SciAm.250c.128C. doi:10.1038/scientificamerican0384-128. PMID 6367033. (판매 국가에 따라 다른 페이지 번호부여: 98–114, 페이지 114 참조) 온라인 기사– 왼쪽 문서 링크 참조
  14. ^ 굿 앤 하딘, 8장
  15. ^ Harris, Robert L. (1999). Information graphics : a comprehensive illustrated reference ([Nachdr.] ed.). Oxford: Oxford University Press. p. 143. ISBN 9780195135329.
  16. ^ a b Data Design by Juergen Kai-Uwe Brock on iBooks. iBooks. Retrieved 2017-06-10.
  17. ^ 친절, 페이지 509
  18. ^ "Florence Nightingale's Statistical Diagrams". Retrieved 2010-11-22.
  19. ^ "Multi-level Pie Charts". www.neoformix.com.
  20. ^ 웨버 리처드, 허버트 릭, 장브크 웰"컴퓨터 기반 경제 모델로부터의 출력을 시각화하는 공간 채우기 기술"
  21. ^ "Feitelson, Dror (2003) Comparing Partitions With Spie Charts" (PDF). 2003. Retrieved 2010-08-31.
  22. ^ a b Kosara, Robert; Skau, Drew (2016). "Judgment Error in Pie Chart Variations". EuroVis.
  23. ^ Krygier, John (28 August 2007). "Perceptual Scaling of Map Symbols". makingmaps.net. Retrieved 3 May 2015.
  24. ^ 클리블랜드, 86~87페이지
  25. ^ 심킨, D. & 헤스티, R. (1987년)그래프 인식의 정보 처리 분석.미국통계학회지, 82(398), 454.doi:10.2307/2289447.Kosara, Robert (13 April 2011). "In Defense of Pie Charts". Retrieved April 13, 2011.
  26. ^ Spence, Ian; Lewandowsky, Stephan (1 January 1991). "Displaying proportions and percentages". Applied Cognitive Psychology. 5 (1): 61–77. doi:10.1002/acp.2350050106.
  27. ^ "An Illustrated Tour of the Pie Chart Study Results". eagereyes. 2016-06-28. Retrieved 2016-11-28.
  28. ^ Skau, Drew; Kosara, Robert (2016). "Arcs, Angles, or Areas: Individual Data Encodings in Pie and Donut Charts". EuroVis.
  29. ^ "A Reanalysis of A Study About (Square) Pie Charts from 2009". eagereyes. 2016-07-11. Retrieved 2016-11-28.

추가 정보

외부 링크

Wikimedia Commons에는 파이 차트와 관련된 미디어가 있습니다.