빈도(통계)

통계학에서 $이벤트{\displaystyle }$i의$$ 빈도($또는$ 절대 빈도$)$는 관찰이 실험 또는 ^{[1]: 12–19} 연구에서 발생/기록된 $횟수{\displaystyle {}_{}}$ $($ $displaystyle$ $n_{i$})이다$$.이러한 빈도는 종종 그래픽 또는 표 형식으로 표시됩니다.

종류들

누적 빈도는 정렬된 ^{[1]: 17–19} 이벤트 목록의 특정 지점 또는 그 이하의 모든 이벤트의 절대 빈도의 합계입니다.

이벤트의 상대 주파수(또는 경험적 확률)는 총 이벤트 수에 의해 정규화된 절대 주파수입니다.

${\displaystyle f_{i}=flac {n_{i}}{N}=flac {n_{i}}{\sum _{j}n_{j}}}.}$

모든 $사건{\displaystyle }$i에 대한 $($$표시 스타일$$$f_$${$i$$})$ $값$을 플롯하여 도수 분포를 생성할 수 있습니다.

$특정$i에 ${\displaystyle \mathrm{대해}}$ n i ${\displaystyle {}_{}}$0 { $displaystyle$n _ { $i$}$$$=$0 인$$ $경우{\displaystyle {}_{}}$ 의사 카운트를 추가할 수 있습니다.

도수 분포 묘사

빈도 분포는 서로 배타적인 클래스와 클래스 내의 발생 횟수로 분할된 데이터의 요약된 그룹을 보여줍니다.선거 결과, 특정 지역의 소득, 일정 기간 내 상품 판매량, 졸업생 학자금 대출액 등을 보여주기 위해 미조직 데이터를 두드러지게 보여주는 방식이다.빈도 분포에 사용할 수 있는 그래프로는 히스토그램, 꺽은선형 차트, 막대 차트 및 원형 차트 등이 있습니다.도수 분포는 질적 데이터와 정량적 데이터 모두에 사용됩니다.

건설

1. 클래스 수를 결정합니다.클래스가 너무 많거나 너무 적으면 데이터 세트의 기본 모양이 드러나지 않을 수 있으며, 그러한 빈도 분포를 해석하는 것도 어려울 수 있습니다.이상적인 클래스 수는 ${\displaystyle \text{클래스}}$수 ${\displaystyle =}$ ${\displaystyle C}$ ${\displaystyle =}$ ${\displaystyle 1}$+${\displaystyle 3.3}$ ${\displaystyle \log }$ ${\displaystyle }$ \ $displaystyle${$text${ $number of$ class } =$C =$1 +$3.3$ \ $log$ n$$（ log base 10 ） byた ${\displaystyle =}$ ${\displaystyle n\sqrt{}}$\ $displaystyle$ C =$sqrt${ $n$} ） :::::::::::: 。모집단 통계량과 같은 대규모 데이터 집합에는 너무 큽니다.)그러나 이러한 공식은 어려운 규칙이 아니며 공식에 의해 결정되는 클래스 수가 항상 처리되는 데이터에 정확하게 적합하지는 않을 수 있습니다.
2. 최소 및 최대 데이터 값을 찾아 데이터 범위(범위 = 최대 – 최소)를 계산합니다.범위는 클래스 간격 또는 클래스 폭을 결정하는 데 사용됩니다.
3. h로 표시되고 h ${\displaystyle =}$ ${\displaystyle \frac{\text{range number of}}{}}$classes { $displaystyle$ h =$range frac {$ $\$ text {$number of$ classes$$}}}$$로 얻을 수 있는 클래스의 폭을 결정합니다($모든$ 클래스에 대해 클래스 간격이 동일하다는 것을 나타냅니다).

일반적으로 클래스 간격 또는 클래스 폭은 모든 클래스에서 동일합니다.모든 클래스는 데이터 내의 최저값(최소값)에서 최고값(최대값)까지의 거리를 커버해야 합니다.도수 분포에서는 균등한 클래스 간격이 선호되지만, 특정 상황에서는 클래스 간에 관측치를 적절히 분산하고 빈 클래스 또는 거의 빈 클래스를 많이 ^[2]피하려면 불균등한 클래스 간격(예: 로그 간격)이 필요할 수 있습니다.

1. 개개의 클래스 제한을 결정하고 임의의 첫 번째 클래스의 적절한 시작점을 선택합니다.최소값보다 작거나 같을 수 있습니다.보통 이 값은 최소값보다 먼저 시작되며 중간점(첫 번째 클래스의 하한과 상한의 평균)이 적절히^{[clarification needed]} 배치됩니다.
2. 관찰을 가져와 해당 관찰이 속한 클래스에 대해 세로 막대()를 표시합니다.마지막 관측까지 연속 집계가 유지됩니다.
3. 필요에 따라 주파수, 상대 주파수, 누적 주파수 등을 찾습니다.

다음으로 ^[3]빈도를 나타내는 일반적인 방법을 나타냅니다.

히스토그램

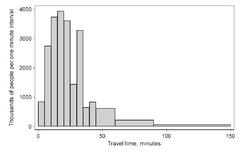
히스토그램은 인접한 직사각형 또는 정사각형(일부 상황에서는)으로 표시되는 간격의 관측 빈도에 비례하는 면적을 가진 표화된 빈도를 나타냅니다.직사각형의 높이는 간격의 주파수 밀도(즉, 주파수를 간격의 폭으로 나눈 값)와도 같습니다.히스토그램의 총 면적은 데이터 수와 같습니다.상대 주파수를 표시하는 히스토그램을 정규화할 수도 있습니다.그런 다음 여러 범주에 속하는 사례의 비율을 나타내며, 총 면적은 1이다.범주는 일반적으로 변수의 겹치지 않는 연속된 간격으로 지정됩니다.카테고리(간격)는 인접해 있어야 하며 종종 같은 ^[4]크기로 선택됩니다.히스토그램의 직사각형은 원래 변수가 ^[5]연속형임을 나타내기 위해 서로 접촉하도록 그려집니다.

막대 그래프

막대 차트 또는 막대 그래프는 직사각형 막대의 길이가 나타내는 값에 비례하는 차트입니다.막대는 수직 또는 수평으로 플롯할 수 있습니다.세로 막대 차트는 세로 막대 차트라고도 합니다.

도수 분포표

도수 분포 표는 하나 이상의 변수가 표본에서 사용하는 값의 배열입니다.표의 각 엔트리는 특정 그룹 또는 간격 내의 값 발생 빈도 또는 카운트를 포함하며, 이와 같이 표는 샘플 내의 값 분포를 요약합니다.

일변량(=단일 변수) 주파수 표의 예입니다.설문조사 질문에 대한 각 응답의 빈도를 나타냅니다.

순위	동의도	번호
1	강력히 동의하다	22
2	어느 정도 동의하다	30
3	확실하진 않다.	20
4	다소 동의하지 않다	15
5	강하게 반대하다	15

다른 표 방식은 각 빈이 값의 범위를 포함하도록 값을 빈으로 집계합니다.예를 들어, 학급 내 학생들의 키는 다음과 같은 빈도 표로 정리될 수 있습니다.

높이 범위	학생수	누적수
5.0피트 미만	25	25
5.0~5.5피트	35	60
5.5~6.0피트	20	80
6.0~6.5피트	20	100

공동 도수 분포

이변량 결합 빈도 분포는 종종 (쌍방향) 분할표로 나타납니다.

한계 빈도를 갖는 이원 분할표

	춤	스포츠	TV	총
남자들	2	10	8	20
여성들.	16	6	8	30
총	18	16	16	50

총 행과 총 열은 한계 빈도 또는 한계 분포를 보고하는 반면, 표의 본문은 공동 ^[6]도수를 보고합니다.

해석

확률의 주파수 해석에서는 일련의 시험 길이가 경계 없이 증가함에 따라 주어진 사건이 발생하는 실험의 비율이 한계 상대 ^[7][8]주파수로 알려진 고정 값에 근접할 것으로 가정한다.

이 해석은 종종 베이지안 확률과 대조된다.사실, '자주파'라는 용어는 1949년 M. G. 켄달에 의해 그가 "비자주파"^[9][10]라고 불렀던 베이시안들과 대조하기 위해 처음 사용되었다.그는 관찰했다

3…우리는 크게 두 가지 태도를 구별할 수 있다.누군가는 확률을 '합리적인 믿음의 정도' 혹은 비슷한 생각이라고 생각한다.두 번째는 사건의 발생 빈도 또는 '집단' 또는 '집단'의 상대적 비율 측면에서 확률을 정의한다. (p.101)

...

12. 빈발자와 비빈발자의 차이는 (내가 그렇게 불러도 좋겠지만) 주로 그들이 다루고 싶어하는 영역의 차이에 기인한다고 생각할 수 있다.(p.104).

...

그렇지 않다고 단언합니다.빈발주의자와 비빈발주의자의 본질적인 차이는, 내 생각에, 전자는 의견의 문제가 풍기는 것을 피하기 위해, 실제든 가상이든, 인구의 객관적인 속성으로 가능성을 정의하려고 하는 반면, 후자는 그렇지 않다는 것이다.[오리지널]

적용들

주파수 표 형식의 데이터 관리 및 조작은 원시 데이터 조작보다 훨씬 간단합니다.이러한 표에서 중위수, 평균, 표준 편차 등을 계산하는 간단한 알고리즘이 있습니다.

통계 가설 테스트는 빈도 분포 간의 차이와 유사성의 평가에 기초한다.이 평가에는 평균 및 중위수 같은 중심 경향 또는 평균의 측정값과 표준 편차 또는 분산과 같은 변동성 또는 통계 분산의 측정값이 포함됩니다.

도수분포는 평균과 중위수가 유의하게 다를 경우 또는 비대칭일 경우 왜곡된다고 합니다.도수 분포의 첨도는 히스토그램의 양 끝에 나타나는 극단값(외측값)의 비율에 대한 측도입니다.분포가 정규 분포보다 특이 확률이 높으면 렙토쿠르틱이고, 특이 확률이 낮으면 편평성이라고 합니다.

문자 빈도 분포는 암호를 해독하는 빈도 분석에도 사용되며, 서로 다른 언어의 문자의 상대적 빈도를 비교하는데 사용되며, 그리스어, 라틴어 등과 같은 다른 언어도 자주 사용됩니다.

「 」를 참조해 주세요.

• 비주기 주파수

• 데이터수
• 교차표
• 누적분포함수
• 누적 주파수 분석
• 경험적 분포 함수

• 대수의 법칙
• 주파수 아날로그로서의 멀티셋 다중성
• 확률밀도함수
• 확률 해석
• 통계적 규칙성
• 단어 빈도

레퍼런스