치환 시험

치환 검정(재랜덤화 검정이라고도 함)은 모순에 의한 증명을 사용하는 정확한 통계 가설 검정입니다.치환 검사에는 두 개 이상의 표본이 포함됩니다.귀무 가설은 모든 표본이 동일한 $H_{0}:F=G$ $H_{0}:F=G$ 0 $H_{0}:F=G$ : $H_{0}:F=G$ $H_{0}:F=G$ {\ $displaystyle H_{0:F=G$ 에서 나온다는 것이며 귀무 가설에서는 관측된 데이터의 가능한 재배열 하에서 시험 통계량의 가능한 모든 값을 계산하여 검정 통계량의 분포를 구한다.따라서 치환 테스트는 재샘플링의 한 형태입니다.

치환 검정은 귀무 가설에 따른 대리 데이터가 ^[1]원래 데이터의 치환을 통해 얻어지는 대리 데이터 검정으로 이해할 수 있습니다.

즉, 실험 설계에서 피실험자에게 처리를 할당하는 방법은 해당 설계의 분석에 반영된다.귀무 가설에서 레이블을 교환할 수 있는 경우 결과 검정 결과에서 정확한 유의 수준이 생성됩니다. 교환 가능성을 참조하십시오.그런 다음 검정에서 신뢰 구간을 도출할 수 있습니다.이 이론은 1930년대 로널드 피셔와 E. J. G. 피트먼의 작품에서 발전했다.

치환 검정은 랜덤화 ^[2]검정과 혼동해서는 안 됩니다.

방법

랜덤 값 4개 및 5개로 구성된 집합에 대해 계산되는 치환 테스트의 애니메이션입니다.빨간색으로 표시된 4개의 값은 한 분포에서 추출되고 파란색으로 표시된 5개의 값은 다른 분포에서 추출됩니다. 두 분포의 평균 값이 서로 다른지 여부를 검정하려고 합니다.첫 번째 분포의 평균이 두 번째 분포의 평균보다 높다는 가설이고, 귀무 가설은 두 표본 그룹이 동일한 분포에서 추출된다는 것입니다.4개의 값을 한 그룹에 넣고 5개를 다른 그룹에 넣는 방법에는 126가지가 있습니다(9-선택-4 또는 9-선택-5).

이

중 하나는 원래 라벨에 따른 것이고, 나머지 125개는 표시된 평균

{\hat {\mu }}_{1}-{\hat {\mu }}_{2}

의 히스토그램을 생성하는 "변환"입니다

{\hat {\mu }}_{1}-{\hat {\mu }}_{2}

{\hat {\mu }}_{1}-{\hat {\mu }}_{2}

^

{\hat {\mu }}_{1}-{\hat {\mu }}_{2}

-

{\hat {\mu }}_{1}-{\hat {\mu }}_{2}

^ 2 {

displaystyle

{ \

mu

} _ {

1

} - { \

hat

{

mu }

}

_

{

{\hat {\mu }}_{1}-{\hat {\mu }}_{2}

} 。가설의 p-값은 원래 표본의 평균 차이보다 크거나 큰 차이를 제공하는 순열의 비율로 추정됩니다.이 예제에서는 p =

5%

수준

에서 귀무

가설을 기각할 수 없습니다.

치환 테스트의 기본 개념을 설명하기 위해 샘플 평균이 ${\bar {x}}_{A}$ 인 $A$ 와 B(\ $displaystyle$ $A$ $)$ 와 $A$ B $(\displaystyle$ B $)$ 에서 $B$ 각 개인에 대해 랜덤 $X_{A}$ X $(\$ $})$ 와 $X_A$ X $X_{B}$ $(\$ $displaystyle X_$ ${B$ $})$ 를 $X_B$ $\bar{x}_{A}$ 수집한다고 가정합니다. ${\bar {x}}_{B}$ B ( \ $displaystyle$ { $x } _$ { $B$ ) 。 $X_{B}$ $,$ X A ( \ $displaystyle X$ _ $X_{A}$ { $X_{B}$ } $X_{B}$ )와 X B ( \ $displaystyle$ X _ { B $X_{B}$ } )가 $X_{B}$ 같은 분포로부터 온 것인지 알고 $X_{A}$ . $n_{A}$ A $(\$ 와 $n_{A}$ n $(\$ 를 $n_{B}$ 각 그룹에서 수집한 샘플 사이즈로 합니다.치환 테스트는 표본 평균 간의 관측된 차이가 $A에서$ 된 데이터가 $B에서$ 추출된 데이터와 동일한 분포에서 추출된 것이라는 귀무 가설 $_{0}$ 0 $({$ $displaystyle_$ ${0$ $B$ 을 $_{0}$ 일부 유의 수준에서 기각할 수 있을 만큼 충분히 큰지 여부를 판단하기 위해 고안되었습니다.

테스트는 다음과 같이 진행됩니다.먼저 두 표본 간의 평균 차이를 계산한다. 이것은 검정 통계량의 $T_{\text{obs}}$ 인 T $T_{\text{obs}}$ 이다.

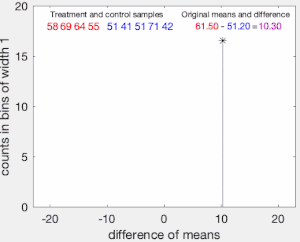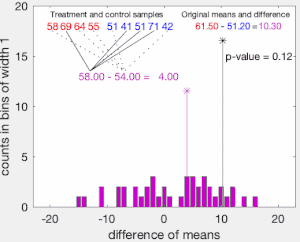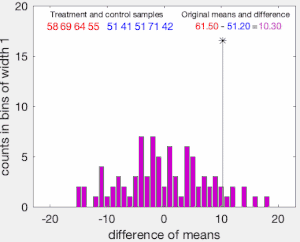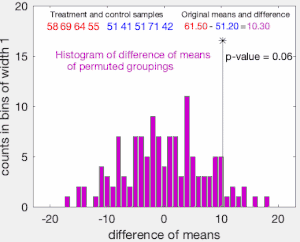
다음으로 그룹 $(\displaystyle$ A $)$ 와 $A$ 그룹B(\ $displaystyle$ B $)$ 의 $B$ 관측치를 취합하고, 취합된 값을 크기 $(\$ 과 $n_{A}$ $n_{B}$ (\ $displaystyle n_{B$ }) $n_{B}$ 의 두 그룹으로 분할할 수 있는 모든 방법에 대해 표본 평균의 차이를 계산하여 기록합니다.그룹 라벨 A 및 B)의 위쪽에 있습니다.이러한 계산된 차이의 집합은 그룹 레이블이 교환 가능(즉, 랜덤하게 할당됨)하다는 귀무 가설에서 가능한 차이의 정확한 분포입니다.

검정의 단측 p-값은 평균의 $T_{\text{obs}}$ 가 T $T_{\text{obs}}$ 보다 큰 표본 순열의 비율로 계산됩니다.테스트의 양면 p-값은 절대 차이가 $obs {\text{obs$ 보다 큰 샘플링된 순열의 비율로 계산됩니다 $.$

또는 테스트의 목적이 귀무 가설을 거부하거나 거부하지 않는 것일 경우 기록된 차이를 분류한 $T_{\text{obs}}$ T $T_{\text{obs}}$ {\ $text{$ obs}} T obs {\text ${obs$ }}}이 $(1-\alpha )\times 100$ ) 중간 $(1-\alpha )\times 100$ 1 $(1-\alpha )\times 100$ - $(1-\alpha )\times 100$ α) × $(1-\alpha )\times 100$ {\ $display$ $(1-\alpha)\times$ 100 $(1-\alpha )\times 100$ 내에 포함되어 $T_{\text{obs}}$ $\alpha$ 할 수 있다 $.$ $laystyle \alpha$ $\alpha$ 그렇지 않으면 α $\alpha \times 100\%$ × $%(\displaystyle \alpha \times$ 100 $\%)$ $\alpha \times 100\%$ 수준에서 동일한 확률 곡선에 대한 가설을 기각합니다.

파라메트릭 테스트와의 관계

치환 검정은 비모수 통계량의 부분 집합입니다.실험 데이터가 두 처리 그룹에서 측정된 데이터에서 나온다고 가정하면, 이 방법은 두 그룹이 측정된 변수 측면에서 구별되지 않는다는 가정 하에 평균 차이의 분포를 생성한다.그런 다음 관찰된 통계량( $T_{\text{obs}}$ 의 T $T_{\text{obs}}$ obs\ $displaystyle T_{\text{obs}})$ 을 $T_{\text{obs}}$ 사용하여 이 통계량이 어느 정도 특별한지, 즉 치료 후 치료 라벨이 무작위로 추출된 경우 해당 값의 크기를 관찰할 수 있는 가능성을 확인할 수 있다.

치환 검정과는 달리, t 검정, F 검정, z 검정 및² θ 검정과 같이 많은 일반적인 "고전적" 통계 검정의 기초가 되는 분포는 이론적 확률 분포에서 얻을 수 있습니다.Fisher의 정확한 검정은 두 이분법 변수 간의 연관성을 평가하기 위해 일반적으로 사용되는 순열 검정의 한 예입니다.표본 크기가 매우 크면 Pearson의 카이-제곱 검정을 통해 정확한 결과를 얻을 수 있습니다.작은 표본의 경우 카이-제곱 기준 분포가 검정 통계량의 확률 분포를 정확하게 설명하는 것으로 가정할 수 없으며, 이 상황에서는 Fisher의 정확한 검정을 사용하는 것이 더 적절합니다.

치환 검정은 모수 검정이 그렇지 않은 많은 상황에서 존재한다(예: 손실이 제곱이 아닌 오차 크기에 비례하는 경우 최적 검정을 도출하는 경우).모든 단순하고 비교적 복잡한 파라메트릭 테스트에는 파라메트릭 테스트와 동일한 검정 통계량을 사용하여 정의되지만 파라메트릭 분석에서 도출된 이론적 분포가 아닌 해당 통계량의 표본별 순열 분포에서 p-값을 얻는 해당 순열 테스트 버전이 있습니다.예를 들어 치환 t-테스트, 치환 test² 연관성 테스트, 분산 비교를 위한 Aly의 치환 버전 등을 구성할 수 있다.

치환 테스트의 주요 단점은 다음과 같습니다.

계산 부하가 높을 수 있으며 계산이 어려운 통계에는 "커스텀" 코드가 필요할 수 있습니다.이건 모든 경우에 다시 쓰여져야 합니다.
주로 p-값을 제공하는 데 사용됩니다.신뢰 영역/간격을 얻기 위해 검정을 반전시키려면 훨씬 더 많은 계산이 필요합니다.

이점

치환 검정은 분포가 알려져 있는지 여부에 관계없이 검정 통계량에 대해 존재합니다.따라서 가설과 대안을 가장 잘 구별하고 손실을 최소화하는 통계량을 선택할 수 있습니다.

치환 테스트는 불균형^[3] 설계 분석 및 범주형, 순서형 및 미터법 데이터의 혼합에 대한 종속적 테스트를 결합하는 데 사용할 수 있다(Pesarin,^{[citation needed]} 2001).또한 정량화된(즉, 숫자로 변환된) 질적 데이터를 분석하는 데 사용할 수 있다.치환 검정은 전통적인 모수 검정(예: t-검정, 분산 분석)^[4]의 기초가 되는 통계적 가정을 충족하지 않는 양자화된 데이터를 분석하는 데 이상적일 수 있습니다. 자세한 내용은 영구 분산 분석을 참조하십시오.

1980년대 이전에는 표본 크기가 작은 데이터 세트를 제외하고 기준 분포를 작성해야 하는 부담이 압도적이었다.

1980년대 이후, 비교적 저렴한 고속 컴퓨터의 결합과 특수한 상황에서 적용할 수 있는 새로운 정교한 경로 알고리즘의 개발로 인해 치환 테스트 방법의 적용이 광범위한 문제에 실용화되었습니다.또한 주요 통계 소프트웨어 패키지에 정확한 테스트 옵션을 추가하고, 광범위한 단일 및 다변수 정확한 테스트를 수행하고 테스트 기반의 "정확한" 신뢰 구간을 계산하기 위한 전문 소프트웨어의 출현을 시작했다.

제한 사항

치환 검정 뒤에 있는 중요한 가정은 관측치가 귀무 가설에서 교환 가능하다는 것입니다.이 가정의 중요한 결과는 정규성 가정 하에서 위치 차이 검정(순열 t-검정 등)에 동일한 분산이 필요하다는 것입니다.이 점에서 치환 t-검정은 기존의 학생 t-검정과 동일한 약점을 공유한다(베렌스-피셔 문제).이 상황에서 세 번째 대안은 부트스트랩 기반의 테스트를 사용하는 것입니다.Good(2005)^{[citation needed]}는 치환 테스트와 부트스트랩 테스트의 차이를 다음과 같은 방법으로 설명합니다. "퍼레이션은 분포에 관한 가설을 검정하고 부트스트랩은 모수에 관한 가설을 검정합니다.그 결과 부트스트랩에는 덜 엄격한 전제조건이 수반됩니다."부트스트랩 테스트는 정확하지 않습니다.경우에 따라 적절하게 학습된 통계량에 기초한 치환 검정은 교환성 가정을 ^[5]위반하는 경우에도 점근적으로 정확할 수 있습니다.부트스트랩 기반 테스트는 null $H_{0}:F\neq G$ 0 $H_{0}:F\neq G$ : $H_{0}:F\neq G$ G (\ $displaystyle$ H_ ${$ : )를 사용하여 테스트할 수 있습니다. $따라서 F\neq$ G $}$ 는 동등성 테스트 수행에 적합합니다.

몬테카를로 시험

점근적으로 동등한 순열 테스트는 데이터의 순서가 너무 많아 편리한 방법으로 완전한 열거를 가능하게 할 수 없을 때 생성될 수 있습니다.이는 몬테카를로 표본 추출에 의한 기준 분포를 생성함으로써 이루어지며, 이는 가능한 반복실험의 소량(전체 순열 수에 상대적인) 랜덤 표본을 취한다.모든 데이터셋의 모든 치환 테스트에 이를 적용할 수 있다는 사실은 적용된 통계 영역에서 중요한 돌파구였다.이 접근법에 대한 가장 오래된 언급은 에덴과 예이츠(1933년)와 드와스(1957년)^[6]^[7]이다.이러한 유형의 치환 테스트는 대략 치환 테스트, 몬테카를로 치환 테스트 또는 랜덤 치환 테스트 ^[8]등 다양한 이름으로 알려져 있습니다.

$N$ {\ $displaystyle$ N $}$ 랜덤 $N$ 순열 후 이항 분포를 기반으로 p-값에 대한 신뢰 구간을 얻을 수 있습니다(이항 비율 신뢰 구간 참조).예를 들어, $N=10000$ $N=10000$ 10000 $N=10000$ ${$ $\left[{\hat {p}}-z{\sqrt {\frac {0.05(1-0.05)}{10000}}},{\hat {p}}+z{\sqrt {\frac {0.05(1-0.05)}{10000}}}\right]=[0.045,0.055]$ N $=$ $displaystyle$ ${\widehat {p}}=0.05$ n} $=$ 0. $05 {displaystyle$ {p $} =$ 0. $05$ 인 경우 $,$ 실제 ${\widehat {p}}=0.05$ p { $displaystyle$ p $}$ 에 대한 99% 신뢰 구간은 [p $\left[{\hat {p}}-z{\sqrt {\frac {0.05(1-0.05)}{10000}}},{\hat {p}}+z{\sqrt {\frac {0.05(1-0.05)}{10000}}}\right]=[0.045,0.055]$ - z $\left[{\hat {p}}-z{\sqrt {\frac {0.05(1-0.05)}{10000}}},{\hat {p}}+z{\sqrt {\frac {0.05(1-0.05)}{10000}}}\right]=[0.045,0.055]$ 입니다. $\left[{\hat {p}}-z{\sqrt {\frac {0.05(1-0.05)}{10000}}},{\hat {p}}+z{\sqrt {\frac {0.05(1-0.05)}{10000}}}\right]=[0.045,0.055]$ $\left[{\hat {p}}-z{\sqrt {\frac {0.05(1-0.05)}{10000}}},{\hat {p}}+z{\sqrt {\frac {0.05(1-0.05)}{10000}}}\right]=[0.045,0.055]$ - $\left[{\hat {p}}-z{\sqrt {\frac {0.05(1-0.05)}{10000}}},{\hat {p}}+z{\sqrt {\frac {0.05(1-0.05)}{10000}}}\right]=[0.045,0.055]$ $\left[{\hat {p}}-z{\sqrt {\frac {0.05(1-0.05)}{10000}}},{\hat {p}}+z{\sqrt {\frac {0.05(1-0.05)}{10000}}}\right]=[0.045,0.055]$ , $\left[{\hat {p}}-z{\sqrt {\frac {0.05(1-0.05)}{10000}}},{\hat {p}}+z{\sqrt {\frac {0.05(1-0.05)}{10000}}}\right]=[0.045,0.055]$ + $\left[{\hat {p}}-z{\sqrt {\frac {0.05(1-0.05)}{10000}}},{\hat {p}}+z{\sqrt {\frac {0.05(1-0.05)}{10000}}}\right]=[0.045,0.055]$ 0. $\left[{\hat {p}}-z{\sqrt {\frac {0.05(1-0.05)}{10000}}},{\hat {p}}+z{\sqrt {\frac {0.05(1-0.05)}{10000}}}\right]=[0.045,0.055]$ ( $\left[{\hat {p}}-z{\sqrt {\frac {0.05(1-0.05)}{10000}}},{\hat {p}}+z{\sqrt {\frac {0.05(1-0.05)}{10000}}}\right]=[0.045,0.055]$ - 0. $\left[{\hat {p}}-z{\sqrt {\frac {0.05(1-0.05)}{10000}}},{\hat {p}}+z{\sqrt {\frac {0.05(1-0.05)}{10000}}}\right]=[0.045,0.055]$ $\left[{\hat {p}}-z{\sqrt {\frac {0.05(1-0.05)}{10000}}},{\hat {p}}+z{\sqrt {\frac {0.05(1-0.05)}{10000}}}\right]=[0.045,0.055]$ $\left[{\hat {p}}-z{\sqrt {\frac {0.05(1-0.05)}{10000}}},{\hat {p}}+z{\sqrt {\frac {0.05(1-0.05)}{10000}}}\right]=[0.045,0.055]$ ] $\left[{\hat {p}}-z{\sqrt {\frac {0.05(1-0.05)}{10000}}},{\hat {p}}+z{\sqrt {\frac {0.05(1-0.05)}{10000}}}\right]=[0.045,0.055]$ [ $\left[{\hat {p}}-z{\sqrt {\frac {0.05(1-0.05)}{10000}}},{\hat {p}}+z{\sqrt {\frac {0.05(1-0.05)}{10000}}}\right]=[0.045,0.055]$ . $\left[{\hat {p}}-z{\sqrt {\frac {0.05(1-0.05)}{10000}}},{\hat {p}}+z{\sqrt {\frac {0.05(1-0.05)}{10000}}}\right]=[0.045,0.055]$ $\left[{\hat {p}}-z{\sqrt {\frac {0.05(1-0.05)}{10000}}},{\hat {p}}+z{\sqrt {\frac {0.05(1-0.05)}{10000}}}\right]=[0.045,0.055]$ 0 $\left[{\hat {p}}-z{\sqrt {\frac {0.05(1-0.05)}{10000}}},{\hat {p}}+z{\sqrt {\frac {0.05(1-0.05)}{10000}}}\right]=[0.045,0.055]$ 055 $\left[{\hat {p}}-z{\sqrt {\frac {0.05(1-0.05)}{10000}}},{\hat {p}}+z{\sqrt {\frac {0.05(1-0.05)}{10000}}}\right]=[0.045,0.055]$ ]{ $displaystyle \left$ [ { \ $hat$ { p $}$ - $zsqrt$ { 0. $05$ ( 1 - $0$ . 05) } } 、 { hat { $prac$ { 05 $}$ $} 、$ { $05$ . $05$ . $05$ } $}$

한편, p-값을 추정하는 목적은 p $α($ 으로 α $\alpha =0.05$ 0. $\alpha =0.05$ \ $displaystyle$ \ $scriptstyle$ \ $alpha$ $p\leq \alpha$ 여부를 결정하는 것입니다. $\scriptstyle \ \alpha$ 서 α $(\$ \scriptstyle \alpha $\scriptstyle \ \alpha$ })는 $\scriptstyle\ \alpha$ 귀무 가설이 기각되는 임계값입니다( $\alpha =0.05$ 으로 α = 0. $05$ \ $displaystyle=$ 0.05 $).$ 위의 예에서 신뢰 구간은 p-값이 0.05보다 작을 확률이 대략 50%임을 알려준다. 즉, 귀무 가설을 $\alpha =0.05$ α $\alpha =0.05$ 0. $(\displaystyle \alpha = 0$ .05 $\alpha =0.05$ 에서 기각해야 하는지 여부가 완전히 불분명하다.

$\alpha$ α에 대해 p $p\leq \alpha$ {\ $displaystyle p$ $\leq \alpha$ $\alpha$ 가 $p\leq \alpha$ $p\leq \alpha$ 한 경우에만 p $p\leq \alpha$ {\ $displaystyle$ p $\leq \alpha}$ 라는 $p\leq \alpha$ 문장이 참인지 거짓인지 매우 낮은 확률로 확인될 때까지 시뮬레이션을 계속하는 것이 논리적이다.오류(는 p^하다는 확률;α{\displaystyle{\widehat{p}}>\alpha}사실 p≤ α{\displaystyle p\leq \alpha}또는 그 반대로)의 허용 확률, 얼마나 많은 순열을 생성할 때 하는 문제를 볼 수 없을 정도로 문제에 묶여 있는 ϵ{\displaystyle \epsilon}.이제 그만생성 순열, 모의 실험의 결과를 지금까지 살고 있던 주문다는 결론에(그것은 동업-≤ α{\displaystyle p\leq \alpha}또는 p>α{\displaystyle p>, \alpha})확률과 최소한 1− ϵ{1-\epsilon\displaystyle}로 큰 정확한 있도록 하기 위해.(ϵ{\displaystyle \epsilo.n} 일반적으로 1/1000과 같이 매우 작은 크기로 선택됩니다.)이를 달성하기 위한 정지 규칙은 최소한의^[9] 추가 계산 비용으로 통합될 수 있는 것으로 개발되었습니다.실제로 실제 기본 p-값에 따라 의사결정이 가상 확실성을 가지고 이루어지기 전에 필요한 시뮬레이션의 수가 상당히 적다는 것을 종종 발견할 수 있다(예: 5개 또는 100개 이하).

테스트 예시

분산의 순열 분석

문학.

원본 참조:

피셔, R.A. (1935년)실험의 디자인, 뉴욕: 하프너
Pitman, E. J. G. (1937년) "모든 모집단의 표본에 적용될 수 있는 중요도 테스트", 왕립통계학회 부록, 4: 119-130 및 225-32(파트 I 및 II).JSTOR 2984124 JSTOR 2983647
Pitman, E. J. G. (1938). "Significance tests which may be applied to samples from any population. Part III. The analysis of variance test". Biometrika. 29 (3–4): 322–335. doi:10.1093/biomet/29.3-4.322.

최신 레퍼런스:

Collingridge, D.S. (2013). "A Primer on Quantitized Data Analysis and Permutation Testing". Journal of Mixed Methods Research. 7 (1): 79–95. doi:10.1177/1558689812454457. S2CID 124618343.
에징턴.E.S.(1995년) 랜덤화 테스트, 제3판뉴욕: Marcel-Dekker
Good, Phillip I. (2005) 가설의 치환, 파라메트릭 및 부트스트랩 테스트, 제3판, Springer ISBN 0-387-98898-X
Good, P (2002). "Extensions of the concept of exchangeability and their applications". Journal of Modern Applied Statistical Methods. 1 (2): 243–247. doi:10.22237/jmasm/1036110240.
Lunneborg, Cliff. (1999) 데이터 분석 by Resampling, Duxbury Press.ISBN 0-534-2210-6.
페사린, F. (2001)다변량 치환 테스트: 생물통계학 어플리케이션의 John Wiley & Sons.ISBN 978-0471496700
Welch, W. J. (1990). "Construction of permutation tests". Journal of the American Statistical Association. 85 (411): 693–698. doi:10.1080/01621459.1990.10474929.

계산 방법:

Mehta, C. R.; Patel, N. R. (1983). "A network algorithm for performing Fisher's exact test in r x c contingency tables". Journal of the American Statistical Association. 78 (382): 427–434. doi:10.1080/01621459.1983.10477989.
Mehta, C. R.; Patel, N. R.; Senchaudhuri, P. (1988). "Importance sampling for estimating exact probabilities in permutational inference". Journal of the American Statistical Association. 83 (404): 999–1005. doi:10.1080/01621459.1988.10478691.
Gill, P. M. W. (2007). "Efficient calculation of p-values in linear-statistic permutation significance tests" (PDF). Journal of Statistical Computation and Simulation. 77 (1): 55–61. CiteSeerX 10.1.1.708.1957. doi:10.1080/10629360500108053. S2CID 1813706.

치환 테스트에 대한 현재 연구

좋아요, P.I. (2012) 재샘플링 방법에 대한 실무자 가이드
Good, P.I. (2005) 가설의 치환, 파라메트릭 및 부트스트랩 테스트
부트스트랩샘플링 튜토리얼
헤스터버그, T.C., D.S. 무어, S. 모나한, A.Clipson, 그리고 R.Epstein (2005) :부트스트랩 메서드 및 치환 테스트, 소프트웨어.
무어, D.S., G. McCabe, W. Duckworth, S.Sclove (2003) :부트스트랩 방식 및 치환 테스트
사이먼, J. L.(1997):재샘플링: [새로운 통계(New Statistics 。
Yu, Chong Ho (2003) :재샘플링 방법: 개념, 애플리케이션 및 정당성. Practical Assessment, Research & Evaluation, 8(19) (통계 부트스트랩)
재샘플링: 컴퓨터와 통계의 결합(ERIC 다이제스트)

레퍼런스

^ Moore, Jason H. "부트스트랩, 치환 테스트 및 대용 데이터 방법"의학 및 생물학 분야 물리학 44.6(1999년): L11.
^ Onghena, Patrick (2017-10-30), Berger, Vance W. (ed.), "Randomization Tests or Permutation Tests? A Historical and Terminological Clarification", Randomization, Masking, and Allocation Concealment (1 ed.), Boca Raton, FL: Chapman and Hall/CRC, pp. 209–228, doi:10.1201/9781315305110-14, ISBN 978-1-315-30511-0, retrieved 2021-10-08
^ "Invited Articles" (PDF). Journal of Modern Applied Statistical Methods. 1 (2): 202–522. Fall 2011. Archived from the original (PDF) on May 5, 2003.
^ Collingridge, Dave S. (11 September 2012). "A Primer on Quantitized Data Analysis and Permutation Testing". Journal of Mixed Methods Research. 7 (1): 81–97. doi:10.1177/1558689812454457. S2CID 124618343.
^ Chung, EY; Romano, JP (2013). "Exact and asymptotically robust permutation tests". The Annals of Statistics. 41 (2): 487–507. arXiv:1304.5939. doi:10.1214/13-AOS1090.
^ Eden, T; Yates, F (1933). "On the validity of Fisher's z test when applied to an actual example of non-normal data. (With five text-figures.)". The Journal of Agricultural Science. 23 (1): 6–17. doi:10.1017/S0021859600052862. Retrieved 3 June 2021.
^ Dwass, Meyer (1957). "Modified Randomization Tests for Nonparametric Hypotheses". Annals of Mathematical Statistics. 28 (1): 181–187. doi:10.1214/aoms/1177707045. JSTOR 2237031.
^ Thomas E. Nichols, Andrew P. Holmes (2001). "Nonparametric Permutation Tests For Functional Neuroimaging: A Primer with Examples" (PDF). Human Brain Mapping. 15 (1): 1–25. doi:10.1002/hbm.1058. hdl:2027.42/35194. PMC 6871862. PMID 11747097.
^ Gandy, Axel (2009). "Sequential implementation of Monte Carlo tests with uniformly bounded resampling risk". Journal of the American Statistical Association. 104 (488): 1504–1511. arXiv:math/0612488. doi:10.1198/jasa.2009.tm08368. S2CID 15935787.

[1] Moore, Jason H. "부트스트랩, 치환 테스트 및 대용 데이터 방법"의학 및 생물학 분야 물리학 44.6(1999년): L11.

[2] Onghena, Patrick (2017-10-30), Berger, Vance W. (ed.), "Randomization Tests or Permutation Tests? A Historical and Terminological Clarification", Randomization, Masking, and Allocation Concealment (1 ed.), Boca Raton, FL: Chapman and Hall/CRC, pp. 209–228, doi:10.1201/9781315305110-14, ISBN 978-1-315-30511-0, retrieved 2021-10-08

[3] "Invited Articles" (PDF). Journal of Modern Applied Statistical Methods. 1 (2): 202–522. Fall 2011. Archived from the original (PDF) on May 5, 2003.

[4] Collingridge, Dave S. (11 September 2012). "A Primer on Quantitized Data Analysis and Permutation Testing". Journal of Mixed Methods Research. 7 (1): 81–97. doi:10.1177/1558689812454457. S2CID 124618343.

[5] Chung, EY; Romano, JP (2013). "Exact and asymptotically robust permutation tests". The Annals of Statistics. 41 (2): 487–507. arXiv:1304.5939. doi:10.1214/13-AOS1090.

[6] Eden, T; Yates, F (1933). "On the validity of Fisher's z test when applied to an actual example of non-normal data. (With five text-figures.)". The Journal of Agricultural Science. 23 (1): 6–17. doi:10.1017/S0021859600052862. Retrieved 3 June 2021.

[7] Dwass, Meyer (1957). "Modified Randomization Tests for Nonparametric Hypotheses". Annals of Mathematical Statistics. 28 (1): 181–187. doi:10.1214/aoms/1177707045. JSTOR 2237031.

[8] Thomas E. Nichols, Andrew P. Holmes (2001). "Nonparametric Permutation Tests For Functional Neuroimaging: A Primer with Examples" (PDF). Human Brain Mapping. 15 (1): 1–25. doi:10.1002/hbm.1058. hdl:2027.42/35194. PMC 6871862. PMID 11747097.

[9] Gandy, Axel (2009). "Sequential implementation of Monte Carlo tests with uniformly bounded resampling risk". Journal of the American Statistical Association. 104 (488): 1504–1511. arXiv:math/0612488. doi:10.1198/jasa.2009.tm08368. S2CID 15935787.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

Search