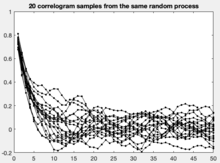
상관도

맨 아래에 "숨겨진" 사인 함수를 포함한 100개의 난수 및 시리즈의 자기 상관(상관도)을 보여주는 그림입니다.

데이터 분석에서 상관도는 상관 통계량의 차트입니다.예를 들어 시계열 분석에서 표본 자기 $r_{h}\,$ $r_{h}\,$ h 대 $($ $지연)$ $h\,$ 의 $그래프는$ $자기$ 상관 그래프이다.교차 상관 관계가 플롯되면 결과를 교차 상관도라고 합니다.

상관도는 데이터 세트의 랜덤성을 확인하는 데 일반적으로 사용되는 도구입니다.랜덤인 경우 모든 시간 지연 분리에 대해 자기 상관 관계가 0에 가까워야 합니다.랜덤하지 않으면 하나 이상의 자기 상관 관계가 유의하게 0이 아닙니다.

또한 상관도는 Box-Jenkins 자기 회귀 이동 평균 시계열 모델의 모델 식별 단계에서 사용된다.자기 상관 관계는 랜덤성에 대해 0에 가까워야 합니다. 분석가가 랜덤성을 검사하지 않으면 많은 통계적 결론의 타당성이 의심됩니다.상관도는 그러한 무작위성을 확인하는 훌륭한 방법입니다.

다변량 분석에서 색상으로 매핑된 영상으로 표시된 상관 행렬을 "코렐로그래픽" 또는 "콜그램"^[1]^[2]^[3]이라고도 합니다.

적용들

상관도는 다음 질문에 대한 답변을 제공하는 데 도움이 될 수 있습니다.

데이터는 랜덤입니까?
관찰이 인접한 관찰과 관련이 있는가?
관찰이 두 번 제거된 관찰과 관련이 있습니까?(등)
관찰된 시계열에서 백색 소음이 발생합니까?
관찰된 시계열은 사인파입니까?
관측된 시계열이 자기 회귀입니까?
관찰된 시계열에 적합한 모델은 무엇입니까?
모델인가?

Y=context{constant}}+{\text{error}

유효하고 충분한가?

$s_{\bar {Y}}=s/{\sqrt {N}}$ $s_{\bar {Y}}=s/{\sqrt {N}}$ Y $s_{\bar {Y}}=s/{\sqrt {N}}$ $=$ / $s_{\bar {Y}}=s/{\sqrt {N}}$ {\ $displaystyle s_{\bar {Y$ }}= $s/{\sqrt {N}}$ 이 $s_{{{\bar {Y}}}}=s/{\sqrt {N}}$ (가) 유효합니까?

^[4]

중요성

랜덤성(고정 모형, 고정 변동, 고정 분포와 함께)은 일반적으로 모든 측정 프로세스의 기반이 되는 네 가지 가정 중 하나입니다.랜덤성 가정은 다음 세 가지 이유로 매우 중요합니다.

대부분의 표준 통계 검정은 무작위성에 의존합니다.테스트 결론의 유효성은 무작위성 가정의 유효성과 직접 관련이 있다.
일반적으로 사용되는 많은 통계 공식은 랜덤성 가정에 의존하며, 가장 일반적인 공식은 표본 평균의 표준 오차를 결정하는 공식이다.

s_{\bar {Y}}}=s/{\sqrt {N}}

여기서 s는 데이터의 표준 편차입니다.많이 사용되긴 하지만 랜덤성 가정이 유지되지 않는 한 이 공식을 사용한 결과는 아무런 가치가 없습니다.

일변량 데이터의 경우 기본 모형은 다음과 같습니다.

Y=context{constant}}+{\text{error}

데이터가 랜덤하지 않으면 이 모형이 잘못되고 잘못된 것이며, 모수(상수 등)에 대한 추정치가 무의미하고 잘못된 값이 됩니다.

자기 상관 추정

지연 h에서의 자기 상관 계수는 다음과 같습니다.

r_{h}=c_{h}/c_{0},

여기서_h c는 자기변환함수입니다.

({displaystyle c_{h}=bar frac {1}{N}}\sum _{t=1}^{N-h}\left(Y_{t}-{\bar {Y}}\오른쪽)\left(Y_{t+h}-{\bar {Y}}\right})\sum

c는₀ 분산 함수입니다.

c_{0}=sum frac {1}{N}\sum _{t=1}^{N}\left(Y_{t}-{\bar {Y}}\right)^2

r의 결과_h 값은 -1에서 +1 사이입니다.

대체견적

일부 소스는 자동변환 함수에 다음 공식을 사용할 수 있습니다.

{\displaystyle c_{h}=sum frac {1}{N-h}\sum _{t=1}^{N-h}\left(Y_{t}-{\bar {Y}}\right)\left(Y_{t+h}-{\bar {Y}}\right}\sum

이 정의는 편견이 적지만, (1/N) 공식은 몇 가지 바람직한 통계 특성을 가지며, 통계 문헌에서 가장 일반적으로 사용되는 형식이다.상세한 것에 대하여는, 채팅 필드의 20 페이지와 49-50 페이지를 참조해 주세요.

상관도를 사용한 통계적 추론

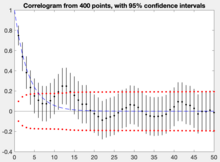
인접 점의 상관 관계가 0.75인 1차 자기 회귀 프로세스의 400점 표본에서 얻은 상관도 예제 및 95% 신뢰 구간(검은색으로는 상관 추정치, 빨간색으로는 약 0)을 이 절의 방정식으로 계산합니다.파란색 점선은 표본 추출 공정의 실제 자기 상관 함수를 나타냅니다.

이전 그림에서와 같은 랜덤 공정의 400점 표본에서 얻은 20개의 상관 그래프.

같은 그래프에서 유의 $(\$ $\alpha \,$ 의 자기 상관 상한과 하한을 그릴 수 있습니다.

B=\pm z_{1-\alpha /2}SE(r_{h})\,

h\,

B=\pm z_{1-\alpha /2}SE(r_{h})\,

±

B=\pm z_{1-\alpha /2}SE(r_{h})\,

1

B=\pm z_{1-\alpha /2}SE(r_{h})\,

-

B=\pm z_{1-\alpha /2}SE(r_{h})\,

/

B=\pm z_{1-\alpha /2}SE(r_{h})\,

B=\pm z_{1-\alpha /2}SE(r_{h})\,

E (

B=\pm z_{1-\alpha /2}SE(r_{h})\,

) ( r h ) {

displaystyle

B

=

\

pm

z _ {1 -

\alpha

/2}

SE

( r

_

{

h

} , ) 、 r

B=\pm z_{1-\alpha /2}SE(r_{h})\,

r_{h}\,

r_{h}\,

h\,

（ \

displaystyle

r

_ {

h

h\,

) 。

자기상관이 이 상한(하한)보다 높은(하한) 경우, 주어진 지연에 자기상관이 없다는 귀무 가설은 유의 수준인 α $(\$ $\alpha \,$ 에서 기각됩니다. 이 테스트는 대략적인 것으로 시계열을 가우스라고 가정합니다.

위의 경우 z는_1−α/2 정규 분포의 분위수이고 SE는 표준 오차이며, MA()) 프로세스에 대한 Bartlett의 공식으로 계산할 수 있습니다.

SE(r_{1})=black {1}{\displayrt {N}}}

SE(r_{h})={\sqrt {\frac {1+2\sum _{i=1}^{h-1}r_{i}^{2}}{N}}}

h>1.\,

SE(r_{h})={\sqrt {\frac {1+2\sum _{i=1}^{h-1}r_{i}^{2}}{N}}}

(

SE(r_{h})={\sqrt {\frac {1+2\sum _{i=1}^{h-1}r_{i}^{2}}{N}}}

h )

SE(r_{h})={\sqrt {\frac {1+2\sum _{i=1}^{h-1}r_{i}^{2}}{N}}}

+

SE(r_{h})={\sqrt {\frac {1+2\sum _{i=1}^{h-1}r_{i}^{2}}{N}}}

i

SE(r_{h})={\sqrt {\frac {1+2\sum _{i=1}^{h-1}r_{i}^{2}}{N}}}

SE(r_{h})={\sqrt {\frac {1+2\sum _{i=1}^{h-1}r_{i}^{2}}{N}}}

-

SE(r_{h})={\sqrt {\frac {1+2\sum _{i=1}^{h-1}r_{i}^{2}}{N}}}

SE(r_{h})={\sqrt {\frac {1+2\sum _{i=1}^{h-1}r_{i}^{2}}{N}}}

SE(r_{h})={\sqrt {\frac {1+2\sum _{i=1}^{h-1}r_{i}^{2}}{N}}}

SE(r_{h})={\sqrt {\frac {1+2\sum _{i=1}^{h-1}r_{i}^{2}}{N}}}

N ( r _ {

display syle SE

( r

_

{ h ) = sum _ {

frac

{

1

+

2

}

{

i = 1

} r _ {

i

} { i } 、

h

SE(r_{h})={\sqrt {\frac {1+2\sum _{i=1}^{h-1}r_{i}^{2}}{N}}}

>

1

}

h>1.\,

。

표시된 예제에서는 최대 4개의 시차로 구분된 시점 사이에 자기 상관 관계가 없다는 귀무 가설을 기각할 수 있습니다.대부분의 긴 기간 동안 자기 상관 관계가 없다는 귀무 가설을 기각할 수 없습니다.

신뢰 대역 생성에는 다음 두 가지 공식이 있습니다.

1. 랜덤성 테스트에 상관도를 사용하는 경우(즉, 데이터에 시간 의존성이 없는 경우) 다음 공식을 사용하는 것이 좋습니다.

\displaystyle \pm {frac {z_{1-\alpha /2}} {\sqrt {N}}}

여기서 N은 표본 크기, z는 표준 정규 분포의 분위수 함수, α는 유의 수준입니다.이 경우 신뢰 대역의 너비는 표본 크기에 따라 달라집니다.

2. ARIMA 모델을 장착하기 위한 모델 식별 단계에서도 상관도를 사용합니다.이 경우 데이터에 대해 이동 평균 모델을 가정하고 다음과 같은 신뢰 대역을 생성해야 한다.

{{displaystyle \pm z_{1-\alpha /2}{\frac {1}{N}}\left(1+2\sum _{i=1}^{k}r_{i}^2}\오른쪽)}}}

여기서 k는 지연입니다.이 경우 신뢰 대역은 지연이 증가함에 따라 증가합니다.

소프트웨어

상관도는 대부분의 범용 통계 라이브러리에서 사용할 수 있습니다.

상관 그래프:

python pandas:pandas.plotting.autocorrelation_plot^[5]
R: 함수acf그리고.pacf

계산:

피톤사본:heatmap,pairplot
R:corrgram^[2]^[3]

레퍼런스

^ Friendly, Michael (19 August 2002). "Corrgrams: Exploratory displays for correlation matrices" (PDF). The American Statistician. Taylor & Francis. 56 (4): 316–324. doi:10.1198/000313002533. Retrieved 19 January 2014.
^ ^a ^b "CRAN – Package corrgram". cran.r-project.org. 29 August 2013. Retrieved 19 January 2014.
^ ^a ^b "Quick-R: Correlograms". statmethods.net. Retrieved 19 January 2014.
^ "1.3.3.1. Autocorrelation Plot". www.itl.nist.gov. Retrieved 20 August 2018.
^ "Visualization § Autocorrelation plot".

추가 정보

Hanke, John E.; Reitsch, Arthur G.; Wichern, Dean W. Business forecasting (7th ed.). Upper Saddle River, NJ: Prentice Hall.
Box, G. E. P.; Jenkins, G. (1976). Time Series Analysis: Forecasting and Control. Holden-Day.
Chatfield, C. (1989). The Analysis of Time Series: An Introduction (Fourth ed.). New York, NY: Chapman & Hall.

외부 링크

자기 상관도

이 문서에는 미국 국립표준기술연구소 웹사이트 https://www.nist.gov의 퍼블릭 도메인 자료가 포함되어 있습니다.

[1] Friendly, Michael (19 August 2002). "Corrgrams: Exploratory displays for correlation matrices" (PDF). The American Statistician. Taylor & Francis. 56 (4): 316–324. doi:10.1198/000313002533. Retrieved 19 January 2014.

[cran_corrgram-2] "CRAN – Package corrgram". cran.r-project.org. 29 August 2013. Retrieved 19 January 2014.

[statsmethods_correlograms-3] "Quick-R: Correlograms". statmethods.net. Retrieved 19 January 2014.

[4] "1.3.3.1. Autocorrelation Plot". www.itl.nist.gov. Retrieved 20 August 2018.

[5] "Visualization § Autocorrelation plot".

[1]

[2]

[3]

[4]

[5]

Search

상관도

네임스페이스

더

목차

적용들

중요성