Kruskal-Wall은 일원 분산 분석

순위별 Kruskal-Wallis 검정, Kruskal-Wallis H 검정^[1](William Kruskal and W의 이름을 따서 명명됨). Allen Wallis) 또는 일원 분산 분석(일원^[1] 분산 분석)은 표본이 동일한 분포에서 비롯되는지 여부를 검정하는 비모수적 방법입니다.^[2][3][4] 표본 크기가 같거나 다른 두 개 이상의 독립적인 표본을 비교하는 데 사용됩니다. 이 검정은 두 그룹만 비교하는 데 사용되는 Mann-Whitney U 검정을 확장합니다. Kruskal-Wallis 검정의 모수 등가물은 일원 분산 분석(ANOVA)입니다.

유의한 Kruskal-Wallis 검정은 적어도 하나의 표본이 다른 하나의 표본을 확률적으로 지배한다는 것을 나타냅니다. 이 검정에서는 이 확률적 우세가 어디에서 발생하는지 또는 몇 쌍의 그룹이 확률적 우세를 얻는지를 식별하지 못합니다. 확률적 우세에 대한 특정 표본 쌍을 분석하기 위해 던 검정, ^[5]본페로니 보정을 사용한 쌍별 Mann-Whitney 검정 ^[6]또는 더 강력하지만 덜 알려진 Conover-Iman 검정이 사용되기도 합니다^[6].

치료가 반응 수준에 유의한 영향을 미치고 치료 중에는 다음 순서가 있는 것으로 추정됩니다.^[7] 한 치료는 가장 낮은 반응을 나타내는 경향이 있고 다른 치료는 다음으로 낮은 반응을 나타내는 경향이 있습니다. 비모수적 방법이기 때문에 Kruskal-Wallis 검정은 유사한 일원 분산 분석과 달리 잔차의 정규 분포를 가정하지 않습니다. 만약 연구자가 중앙값의 차이를 제외하고 모든 그룹에 대해 동일한 모양과 척도의 분포를 가정할 수 있다면 귀무 가설은 모든 그룹의 중앙값이 같다는 것입니다. 그리고 다른 가설은 한 그룹의 적어도 하나의 모집단 중위수가 적어도 하나의 다른 그룹의 모집단 중위수와 다르다는 것입니다. 그렇지 않으면 귀무가설의 기각이 위치 이동에서 오는 것인지 또는 집단 분산에서 오는 것인지를 말할 수 없습니다. 이것은 Mann-Whitney 검정에서도 발생하는 것과 동일한 문제입니다.^[8][9][10] 데이터에 잠재적인 이상치가 포함되어 있거나 모집단 분포의 꼬리가 무겁거나 모집단 분포가 유의하게 치우쳐 있으면 크루스칼-월리스 검정이 분산 분석 F-검정보다 처리 간의 차이를 탐지하는 데 더 효과적입니다. 반면, 모집단 분포가 정규 분포이거나 꼬리가 가볍고 대칭인 경우, 분산 분석 F-검정은 일반적으로 귀무 가설이 실제로 기각되어야 할 때 기각될 확률인 검정력이 더 큽니다.^[11][12]

방법

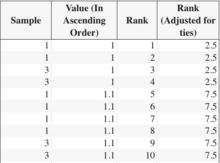
1. 모든 그룹의 모든 데이터의 순위를 함께 매깁니다. 즉, 그룹 구성원 자격을 무시하고 데이터의 순위를 1부터 N까지 매깁니다. 동률이 아니었다면 그들이 받았을 순위의 평균을 동률 값으로 지정합니다.
2. 테스트 통계는 다음에 의해 제공됩니다.

   ${\displaystyle \definecolor {ChromeYellow}{rgb}{1,0.6549019607843137,0.011764705882352941}\definecolor {Green}{rgb}{0,0.5019607843137255,$$0}\definecolor {green}{rgb}{0,0.5019607843137255,0}\definecolor {Blue}{rgb}{0,0,1}\definecolor {Purple}{rgb}{0.5019607843137255,0,0.$$5019607843137255}H$ $=$ $({\$color {$Red$}N}-1$){\frac${\$sum$ _{i$=$1}^{\color${$Orange}g$}{\$color {ChromYellow}n_{i}}({\color {Blue}{\bar {r}}_{i\cdot}}-{\color {Purple}{\bar {r}}^{2}{\sum _{i$=$1}^{\color {Orange}g}\sum _{j$=$1}^{\color {ChromYellow}n_{i}}-{\color {Purple}{\bar {r}}}}-{2}} 여기서

   • $N$ ${\$은(는) 모든 그룹에 대한 총 관찰 수입니다.
   • $g$ ${\$은(는) 그룹 수이다.
   • $n_{}$ ${\$ color ${ChromeYellow}{rgb}{1,0.6549019607843137,0.01176470582352941}\color {ChromeYellow}n_{i}$는 그룹$$ $i{\displaystyle }$ ${\displaystyle$ i$}$의 관측치 수입니다.
   • ${\displaystyle {\mathrm{rj}}_{}}$ ${\$는 그룹 $i{\displaystyle }$ ${\displaystyle i}$의 관측 $j{\displaystyle }$ ${\displaystyle j}$의 순위(모든 관측치 중)입니다$$.
   • $¯$ ${\displaystyle \frac{\underset{}{\overset{}{i}}}{}{\stackrel{}{}}_{}}$⋅ = ∑ j = 1 n $in$ i {\disp${\displaystyle {\stackrel{}{\mathrm{laysty}}}_{}}$le \definecolor {blue}{0,0,1}{\color {blue}{\r}}${\displaystyle {\stackrel{}{\_}}_{}}${i\cdot}}={\frac${\displaystyle {\stackrel{}{}}_{}}${\sum _{j=1}^{n_{i}}{r_{ij}}}{n_{i}}}{n_{i}}}는 그룹 i {\displaystyle i}의$$모든 관측치의 평균 순위입니다.
   • $\stackrel{}{}\stackrel{}{}\frac{\mathrm{r}}{}\stackrel{}{}$$¯$ $=$ 12 $(N$ + 1) ${\te$$\stackrel{}{\mathrm{xtstyl}}$$e$ \definecolor {Purple$}{rgb$}{0$.5019607843137255,$0,0$.5019607843137255}{\$color {Purple}{$\stackrel{}{\backslash }$bar {r}}={\tfrac {1}{2}}(N+1)}은 모든 r개의 {\te$\stackrel{}{\mathrm{xtstyl}}$e \definecolor {Green}{0,0.5019607843137255,0}\defin$\stackrel{}{\mathrm{e\; c}}$olor {rgb}{0,0.5019607843137255,0}\color {Green}r_{ij}}의 평균입니다.
3. 데이터에 연관성이 없는 $경우$ H ${\displaystyle$ H$}$에 대한 식의 분모는 ${\displaystyle \mathrm{정확히}}$(${\displaystyle \mathrm{N}}$- 1${\displaystyle )}$ N${\displaystyle (N}$+ ${\displaystyle 1}$)${\displaystyle }$/ ${\displaystyle 12}$ ${\displaystyle (N-1)$ N$(N+1)/12}$이고 ${\displaystyle \frac{\mathrm{r}}{}\stackrel{}{}}$¯ = N$$+ $12$ {\$displaystyle${\$bar$ {r}}= {\tfrac {N+1}{2}}입니다. 따라서

   ${\displaystyle {\begin{aligned}H&={\frac {12}{N(N+1)}}\sum _{i=1}^{g}n_{i}\left({\bar {r}}_{i\cdot }-{\frac {N+1}{2}}\right)^{2}\\&={\frac {12}{N(N+1)}}\sum _{i=1}^{g}n_{i}{\bar {r}}_{i\cdot }^{2}-\ 3(N+1)\end{aligned}}}$
   마지막 공식에는 평균 순위의 제곱만 포함됩니다.

4. 앞에서 설명한 바로가기 $공식$을 사용하여 $H$ ${\displaystyle$ H$}$를 ${\displaystyle \frac{\underset{}{\overset{}{1}}}{}}$- ∑ ${\displaystyle \frac{{}_{}^{}}{}}$ = ${\displaystyle \frac{1_{}^{}}{}}$ G${\displaystyle \frac{{}_{}^{}}{}}$(${\displaystyle \frac{{}_{}}{}}$3 - ti ) N 3 - N {\displaystyle 1-{\frac {\sum _{i=1}^{G}(t_{i}^{3}-t_{i})}{N^{3}-N}}, 여기서 G는 서로 다른 타이 순위의 그룹화 수이며, 그룹_i i 내에서 특정 값으로 묶이는 묶은 값의 개수입니다. 이 보정은 많은 수의 타이가 있지 않는 한 보통 H의 값에 거의 차이가 없습니다.
5. 다중 표본 비교를 수행할 때 I형 오차가 부풀려지는 경향이 있습니다. ${\displaystyle \frac{\mathbb{따라서}}{}}$ 본페로니 절차는 ¯ = α $k$${\displaystyle${\bar {a}}={\$frac$ {\$alpha$}{\Bbbk}}, 여기서 ¯ {\displaystyle {\bar {a}}는 조정된 유의 수준, α {\displaystyle \alpha}는 초기 유의 수준, $그리고{\displaystyle \mathbb{}}$ k ${\displaystyle \Bbbk}$는 대비의 개수입니다.^[13]
6. 마지막으로 H ${\displaystyle H}$를 주어진 유의성 또는 알파 수준에 대한 테이블 또는 소프트웨어에서 얻은$$ 임계값 ${\displaystyle H_{}}$ c ${\$와 비교하여 귀무 가설의 기각 여부를 결정합니다. $H{\displaystyle }$ ${\displaystyle H}$이(가) ${\displaystyle {Hc}_{}}${\$displaystyle H_{c}}$보다 크면 귀무 가설이 기각됩니다$.$ 가능하면(동선이 없고, 표본이 너무 크지 않음) $H{\displaystyle }$ ${\displaystyle$ H$}$를 $H{\displaystyle }$ ${\displaystyle H}$의 정확한 분포로부터 얻은 임계값과 비교해야 합니다$.$ 그렇지 않으면 H의 분포는 g-1 자유도를 갖는 카이제곱 분포로 근사할 수 있습니다. 일부 ${\displaystyle {ni}_{}}$ ${\$ 값이$$ 작으면(즉, 5 미만) $H{\displaystyle }$ ${\displaystyle$ H$}$의 정확한 확률 분포는 이 카이제곱 분포와 상당히 다를$$ 수 있습니다. 카이제곱 확률 분포의 표를 사용할 수 있는 경우,${\displaystyle {}_{}^{}}$χ α: g${\displaystyle {}_{}^{}}$- $12 {\displaystyle \chi$ _${\alpha :g-1$2}}의 임계값은 g - 1 자유도로 표를 입력하고 원하는 유의도 또는 알파 수준 아래를 보면 알 수 있습니다.
7. 통계량이 유의하지 않으면 표본 간에 확률적 우세의 증거가 없습니다. 그러나 검정이 유의하면 적어도 하나의 표본이 다른 표본을 확률적으로 지배합니다. 따라서 연구자는 개별 표본 쌍 간의 표본 대조 또는 (1) Kruskal-Wallis 검정과 동일한 순위를 적절하게 사용하는 Dunn 검정을 사용한 사후 검정을 사용할 수 있습니다. 그리고 (2)는 Kruskal-Wallis 검정의 귀무 가설에 의해 내포된 통합 분산을 적절하게 사용하여 표본 쌍 중 어느 것이 유의하게 다른지를 결정합니다.^[5] 다중 표본 대조 또는 검정을 수행할 때 유형 I 오류율이 부풀려지는 경향이 있으므로 다중 비교에 대한 우려가 제기됩니다.

정확한 확률표

Kruskal-Wallis 검정의 정확한 확률을 계산하려면 많은 양의 컴퓨팅 리소스가 필요합니다. 기존 소프트웨어는 약 30명 미만의 표본 크기에 대해서만 정확한 확률을 제공합니다. 이러한 소프트웨어 프로그램은 더 큰 표본 크기에 대한 점근 근사에 의존합니다.

더 큰 표본 크기에 대한 정확한 확률 값을 사용할 수 있습니다. Spurrier(2003)는 45명의 참가자에 대한 정확한 확률표를 발표했습니다.^[15] Meyer and Seaman(2006)은 105명의 참가자만큼 큰 표본에 대한 정확한 확률 분포를 만들었습니다.^[16]

$H {\textstyle$ H$}$의 정확한 분포

Choi 등은 ^[17]H ${\displaystyle$ H}의$$정확한 분포를 계산하기 위해 개발된 두 가지 방법을 검토하고 새로운$$방법을 제안했으며 정확한 분포를 카이제곱 근사와 비교했습니다.

예

월별 오존 농도 차이 검정

다음 예제는 뉴욕시에서 1973년 5월 1일부터 9월 30일까지 매일 오존 수치를 측정한 Chambers et al.^[18] 의 데이터를 사용합니다. 데이터는 R 데이터 세트 공기질에 있으며, 분석은 R 함수에 대한 설명서에 포함되어 있습니다. kruskal.test. 월별 오존 값의 상자 그림이 그림에 표시되어 있습니다.

Kruskal-Wallis 검정에서는 오존이 5개월 동안 차이가 있음을 나타내는 유의한 차이(p = 6.901e-06)를 발견했습니다.

크루스칼.검정(오존 ~ 달, 데이터. = 공기질)   크루스칼-월리스 순위 합 시험  데이터.:  오존 타고 달 크루스칼-월리스 기-제곱의 = 29.267, df = 4, p-가치 = 6.901e-06 

어떤 월이 다른지 확인하기 위해 각 월 쌍에 대해 Wilcoxon 검정을 사용하여 사후 검정을 수행하고 다중 가설 검정을 위해 Bonferroni(또는 기타) 보정을 사용할 수 있습니다.

쌍쌍이wilcox.test(공기질$오존, 공기질$달, p.적응을 시키다방법 = 본페로니)    쌍별 비교. 사용. 윌콕슨 순위 합 시험   데이터.:  공기질$오존 그리고. 공기질$달     5      6      7      8      6 1.0000 -      -      -      7 0.0003 0.1414 -      -      8 0.0012 0.2591 1.0000 -      9 1.0000 1.0000 0.0074 0.0325  P 가치 조정의 방법: 봉페로니 

사후 검정 결과 다중 검정에 대한 Bonferroni 보정 후 다음과 같은 차이가 유의한 것으로 나타났습니다(조정 p < 0.05).

• 5개월 대 7개월 및 8개월
• 9개월 대 7개월 및 8개월

실행

크루스칼-월리스 테스트는 많은 프로그래밍 도구와 언어로 구현할 수 있습니다.

• Mathematica는 이 테스트를 위치 등가성 테스트로 구현합니다.^[19]

• MATLAB의 통계 도구 상자에는 가설 검정의 p-값을 계산하고 분산 분석 표를 표시하는 크루스칼왈리스가 있습니다.^[20]
• SAS에는 "NPAR1"이 있습니다.테스트를 위한 WAY" 절차.^[21]
• SPSS는 "Nonparametric Tests" 절차로 테스트를 구현합니다.^[22]
• Minitab에는 "비모수" 옵션에 구현이 있습니다.^[23]
• 파이썬의 SciPy 패키지에는 scipy.stats 기능이 있습니다.kruskal은 테스트 결과와 p-value를 반환할 수 있습니다.^[24]
• R base-package는 kruskal.test를 사용하여 이 테스트를 구현합니다.^[25]
• Java는 Apache Commons에서 제공하는 구현체를 가지고 있습니다.^[26]
• 줄리아에서 패키지 가설Tests.jl에는 Kruskal Wallis Test(그룹::추상벡터{<:Real}...)을 사용하여 p-값을 계산합니다.^[27]

참고 항목

• 일원 분산 분석
• Mann-Whitney U 검정
• 본페로니 검정
• 프리드먼 검정
• Jonckheere's trend test
• 분위기 중앙값 t 검정

참고문헌

더보기

• Daniel, Wayne W. (1990). "Kruskal–Wallis one-way analysis of variance by ranks". Applied Nonparametric Statistics (2nd ed.). Boston: PWS-Kent. pp. 226–234. ISBN 0-534-91976-6.

외부 링크

• 테스트의 온라인 버전