생존 분석

이 문서에는 여러 가지 문제가 있습니다.개선을 돕거나 토크 페이지에서 이러한 문제에 대해 논의해 주십시오.(이러한 템플릿메시지를 삭제하는 방법과 타이밍에 대해 설명합니다) 이 문서는 Wikipedia의 품질 기준을 충족하기 위해 청소가 필요할 수 있습니다.구체적인 문제는 워드프로세서 교정 마크업을 포함한 플레인텍스트(콘텐츠 및 표) 이미지입니다. Wikitext로 변환해야 합니다. 가능하면 이 글을 개선해 주세요. (2019년 9월) (템플릿 메시지 삭제 방법 및 삭제 시기 확인) 이 글은 검증을 위해 추가 인용문이 필요합니다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선하는 데 도움을 주십시오. 조달되지 않은 자재는 제거될 수 있습니다.출처 : '생존 분석'– 뉴스 · 신문 · 서적 · 학자 · JSTOR ( 2021년 4월) (이 템플릿 메시지 삭제 방법 및 삭제 시기 확인) (이 템플릿메시지를 삭제하는 방법과 타이밍을 확인합니다)

생존 분석은 생물학적 유기체의 죽음과 기계 시스템의 고장과 같은 하나의 사건이 발생할 때까지의 예상 기간을 분석하기 위한 통계의 한 분야이다.이 주제는 공학에서는 신뢰성 이론 또는 신뢰성 분석, 경제학에서는 지속시간 분석 또는 지속시간 모델링, 사회학에서는 사건 이력 분석이라고 불린다.생존 분석은 특정 시간을 지나 생존할 인구의 비율이 얼마나 되는지와 같은 특정 질문에 답하기 위해 시도합니다.살아남은 사람들 중 어느 정도 비율로 죽거나 실패할 것인가?사망 또는 실패의 여러 원인을 고려할 수 있습니까?어떻게 특정한 상황이나 특성이 생존 확률을 증가시키거나 감소시키나요?

이러한 질문에 답하려면 "평생"을 정의할 필요가 있습니다.생물학적 생존의 경우, 죽음은 분명하지만 기계적 신뢰성의 경우, 실패가 부분적이거나 정도의 문제이거나 시간에 따라 국부화되지 않는 기계적 시스템이 있을 수 있기 때문에 실패는 명확하게 정의되지 않을 수 있다.생물학적 문제에서도 일부 사건(예: 심장마비 또는 기타 장기 기능 상실)은 동일한 모호성을 가질 수 있습니다.아래에 설명된 이론은 특정 시간에 명확하게 정의된 사건을 가정합니다. 다른 사례는 애매한 사건을 명시적으로 설명하는 모델에 의해 더 잘 처리될 수 있습니다.

보다 일반적으로 생존 분석은 사건 데이터의 모델링을 포함한다. 이 맥락에서 사망 또는 실패는 생존 분석 문헌에서 "사건"으로 간주된다. 전통적으로 각 주제에 대해 하나의 사건만 발생하며, 그 후에 유기체나 메커니즘이 죽거나 파괴된다.반복 이벤트 또는 반복 이벤트 모델은 이러한 가정을 완화합니다.반복 사건에 대한 연구는 시스템 신뢰성과 사회과학 및 의학 연구의 많은 분야에서 관련이 있다.

서바이벌 분석 입문

생존 분석은 다음과 같은 여러 가지 방법으로 사용됩니다.

• 그룹 구성원의 생존 시간을 기술하려면
  • 라이프 테이블
  • 카플란-마이어 곡선
  • 서바이벌
  • 위험 함수
• 둘 이상의 그룹의 생존 시간을 비교하는 방법
  • 로그 순위 테스트
• 범주형 또는 정량적 변수가 생존에 미치는 영향을 설명하는 방법
  • Cox 비례 위험 회귀 분석
  • 모수 생존 모형
  • 서바이벌 트리
  • 생존 랜덤 포레스트

생존 분석에서 공통 용어의 정의

생존 분석에서 일반적으로 사용되는 용어는 다음과 같습니다.

• 이벤트: 사망, 질병 발생, 질병 재발, 회복 또는 기타 관심 경험
• 시간: 관찰 기간의 시작부터 (수술 또는 치료 시작 등) 사건, (ii) 연구 종료, (iii) 연락 두절 또는 연구 중단까지의 시간.
• 관측 중단/관측 중단 관측치:관측 중단은 개별 생존 시간에 대한 정보는 있지만 생존 시간을 정확히 알 수는 없는 경우에 발생합니다.관측 중단 시간 이후 해당 주제에 대해 관측되거나 알려진 것이 없다는 점에서 피검체는 관측 중단됩니다.관측 중단 대상자는 관측 시간이 끝난 후 사건이 발생할 수도 있고 없을 수도 있습니다.
• 생존 함수 S(t):대상자가 시간 t보다 오래 생존할 확률입니다.

예:급성 골수성 백혈병 생존 데이터

이 예는 R의 "생존" 패키지의 급성 골수성 백혈병 생존 데이터 세트 "aml"을 사용한다.데이터 세트는 Miller(1997년)^[1]의 것이며, 질문은 화학 요법의 표준 과정을 추가 주기에 대해 연장해야 하는지('유지') 여부이다.

생존 시간별로 정렬된 AML 데이터 세트가 상자에 표시됩니다.

• 시간은 생존 또는 관측 중단 시간인 "시간" 변수로 표시됩니다.
• 이벤트(암 재발)는 변수 "상태"로 표시됩니다.0 = 사건 없음(차이), 1 = 사건(차이)
• 치료군 : 변수 "x"는 유지관리 화학요법을 받았는지 여부를 나타냅니다.

마지막 관측치(11)는 161주 동안 관측 중단됩니다.관측 중단은 환자가 사건이 발생하지 않았음을 나타냅니다(암 재발 없음).또 다른 실험 대상인 관측치 3은 13주(상태=0)에 관측 중단되었습니다.이 피험자는 13주 동안만 연구되었고, 그 13주 동안 암은 재발하지 않았습니다.이 환자는 13주 동안만 관찰할 수 있도록 연구가 끝날 무렵에 등록되었을 가능성이 있습니다.환자가 스터디 초기에 등록되었지만 후속 조치를 위해 분실되었거나 스터디에서 철수했을 수도 있습니다.이 표에는 다른 피실험자가 16주, 28주 및 45주(상태=0인 그림 17, 6주 및 9주)에 관측 중단되었음을 알 수 있습니다.나머지 모든 피험자는 연구 중에 사건(암 재발)을 경험했다.관심사는 유지된 환자에서 비유지된 환자보다 더 늦게 재발하는지 여부이다.

AML 데이터에 대한 Kaplan-Meier 그림

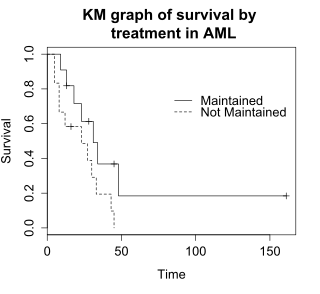
생존함수 S(t)는 피사체가 시간 t보다 더 오래 생존할 확률이다. S(t)는 이론적으로 매끄러운 곡선이지만, 일반적으로 Kaplan-Meier(KM) 곡선을 사용하여 추정한다.그래프에는 AML 데이터에 대한 KM 그림이 표시되며 다음과 같이 해석할 수 있습니다.

• x축은 0(관측이 시작된 시점)부터 마지막 관측 시점까지의 시간입니다.
• y축은 생존하는 피실험자의 비율입니다.시간 0에, 피실험자의 100%는 사건 없이 살아있다.
• 실선(계단과 유사)은 이벤트 발생의 진행을 나타냅니다.
• 수직 강하는 이벤트를 나타냅니다.위의 암표에서 두 피실험자는 5주에, 두 피실험자는 8주에, 한 피실험자는 9주에, 그리고 다른 피실험자는 9주에 사건이 있었다.5주, 8주 등의 이벤트는 해당 시점의 KM 플롯의 수직적 하락으로 나타납니다.
• KM 플롯의 맨 오른쪽 끝에는 161주라는 체크 표시가 있습니다.수직 눈금 표시는 이때 환자가 중도 절단되었음을 나타냅니다.aml 데이터 표에서 5명의 피험자가 13주, 16주, 28주, 45주 및 161주에 검열을 받았다.KM 그림에는 이러한 관측 중단 관측치에 해당하는 5개의 눈금 표시가 있습니다.

AML 데이터에 대한 수명표

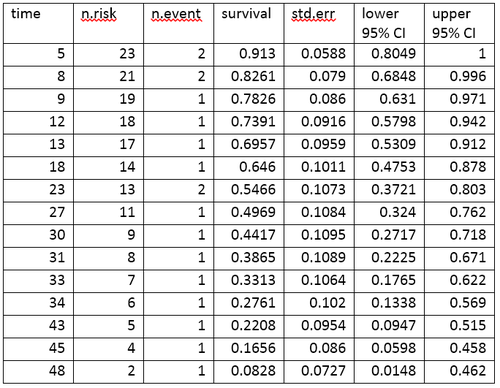
수명표는 사건 발생 횟수와 각 사건 발생 시점의 생존 비율을 기준으로 생존 데이터를 요약합니다.R 소프트웨어를 사용하여 생성된 aml 데이터의 라이프 테이블이 표시됩니다.

수명 표에는 사건 및 각 사건 시점에 생존하는 비율이 요약되어 있습니다.수명 테이블의 열에는 다음과 같은 해석이 있습니다.

• time은 이벤트가 발생하는 시점을 나타냅니다.
• n.risk는 시점 직전에 위험에 처한 피험자의 수, t. "위험"은 피험자가 시간 t 이전에 사건이 없었음을 의미하며 시간 t 이전 또는 시간 t에 대해 검열되지 않는다.
• n.event는 시간 t에 사건이 있는 피실험자의 수입니다.
• 생존은 카플란-마이어 제품 한계 추정치를 사용하여 결정되는 생존 비율이다.
• std.err은 추정 생존의 표준 오차입니다.카플란-마이어 제품 한계 추정치의 표준 오차는 그린우드의 공식을 사용하여 계산되며, 위험 수(표에서 n.위험), 사망자 수(표에서 n.사건), 생존 비율(표에서 생존)에 따라 달라진다.
• 95% CI 하한과 95% CI 상한이 생존 비율에 대한 95% 신뢰 하한 및 상한입니다.

로그 순위 테스트:AML 데이터의 생존 차이 검정

로그 순위 검정은 두 개 이상의 그룹의 생존 시간을 비교합니다.이 예제에서는 AML 데이터에서 유지 관리된 처리 그룹과 유지 관리되지 않은 처리 그룹의 생존 차이에 대해 로그 순위 검정을 사용합니다.그래프에는 처리 그룹별로 구분된 AML 데이터에 대한 KM 그림이 표시되며, 데이터의 변수 "x"로 표시됩니다.

로그 순위 검정의 귀무 가설은 그룹이 동일한 생존을 갖는다는 것입니다.각 사건 발생 시점의 각 시점에서 생존하는 기대 피실험자 수는 각 사건 발생 시 그룹의 위험 피실험자 수에 따라 조정됩니다.로그 순위 검정은 각 그룹의 관측된 이벤트 수가 예상 횟수와 유의하게 다른지 여부를 확인합니다.공식 검정은 카이 제곱 통계량을 기반으로 합니다.로그 순위 통계량이 크면 그룹 간의 생존 시간이 다르다는 증거입니다.로그 순위 통계량은 자유도가 1인 카이 제곱 분포를 근사적으로 가지며 p-값은 카이 제곱 분포를 사용하여 계산됩니다.

예제 데이터의 경우 생존 차이에 대한 로그 순위 검정은 p-값을 p=0.0653으로 제공하므로 알파 수준을 0.05로 가정할 때 처리 그룹의 생존 차이가 유의하지 않습니다.23개 피험자의 표본 크기가 작기 때문에 처리 그룹 간의 차이를 탐지할 수 있는 검정력이 거의 없습니다.카이 제곱 검정은 점근 근사치를 기반으로 하므로 표본 크기가 작은 경우에는 p-값을 주의하여 고려해야 합니다.

Cox 비례 위험(PH) 회귀 분석

카플란-마이어 곡선 및 로그 순위 테스트는 예측 변수가 범주형(예: 약물 대 위약)이거나 범주형으로 취급할 수 있는 소수의 값(예: 약물 선량 0, 20, 50 및 100mg/일)을 취할 때 가장 유용하다.로그 순위 검사와 KM 곡선은 유전자 발현, 백혈구 수 또는 나이와 같은 정량적 예측 변수에는 쉽게 작동하지 않습니다.정량적 예측 변수의 경우 다른 방법은 Cox 비례 위험 회귀 분석입니다.Cox PH 모형은 {0,1} 지시 변수 또는 더미 변수로 인코딩된 범주형 예측 변수와도 작동합니다.로그 순위 테스트는 Cox PH 분석의 특수한 경우이며 Cox PH 소프트웨어를 사용하여 수행할 수 있습니다.

예: 흑색종에 대한 Cox 비례 위험 회귀 분석

이 예에서는 Dalgaard 14장의 흑색종 데이터 세트를 사용합니다.^[2]

데이터는 R 패키지 ISwR에 있습니다.R을 사용한 Cox 비례 위험 회귀 분석에서는 상자에 표시된 결과를 제공합니다.

Cox 회귀 분석 결과는 다음과 같이 해석됩니다.

• 성별은 숫자 벡터(1: 여성, 2: 남성)로 인코딩된다.Cox 모델에 대한 R 요약은 첫 번째 그룹, 즉 남성 대 여성에 상대적인 두 번째 그룹의 위험비(HR)를 제공한다.
• cof = 0.662는 남성 대 여성에 대한 위험 비율의 추정 대수이다.
• exp(coef) = 1.94 = exp(0.662) - 위험비 로그(coef= 0.662)는 exp(coef)를 사용하여 위험비로 변환됩니다.Cox 모델에 대한 요약은 첫 번째 그룹, 즉 남성 대 여성에 대한 두 번째 그룹의 위험 비율을 제공한다.추정 위험률이 1.94인 것은 이러한 데이터에서 남성이 여성보다 사망 위험이 높다는(생존률이 낮다는) 것을 나타냅니다.
• se(coef) = 0.265는 로그 위험 비율의 표준 오차입니다.
• z = 2.5 = cof/se(coef) = 0.662/0.265입니다.coef를 표준 오차로 나누면 z 점수가 나옵니다.
• p=0.013.성별에 대한 z=2.5에 해당하는 p-값은 p=0.013으로 성별 함수로서의 생존에 유의한 차이가 있음을 나타낸다.

요약 출력은 또한 위험 비율에 대한 95% 신뢰 구간(하위 95% 한계 = 1.15, 상한 95% 한계 = 3.26)을 제공합니다.

마지막으로 출력은 모형의 전체 유의성에 대한 세 가지 대체 검정의 p-값을 제공합니다.

• 우도비 검정 = 6.15 on 1 df, p=0.0131
• Wald 검정 = 6.24 on 1 df, p=0.0125
• 점수(로그 순위) 검정 = 1df에서 6.47점, p=0.0110

이 세 가지 검정은 점근적으로 동일합니다.충분히 큰 N에 대해서도 비슷한 결과를 얻을 수 있습니다.작은 N의 경우, 이들은 다소 다를 수 있습니다.마지막 행인 "점수(로그랭크) 테스트"는 로그 순위 테스트의 결과이며, 로그 순위 테스트는 Cox PH 회귀의 특수한 경우이기 때문에 p=0.011로 로그 순위 테스트의 결과와 동일합니다.우도비 검정은 표본 크기가 작을수록 동작이 더 좋으므로 일반적으로 선호됩니다.

흑색종 데이터에서 공변량을 사용하는 Cox 모형

Cox 모형은 추가 공변량을 포함할 수 있도록 하여 로그 순위 검정을 확장합니다.이 예에서는 예측 변수가 연속 공변량인 종양의 두께를 포함하는 흑색종 데이터 세트를 사용합니다(예: 이름 = "유사").

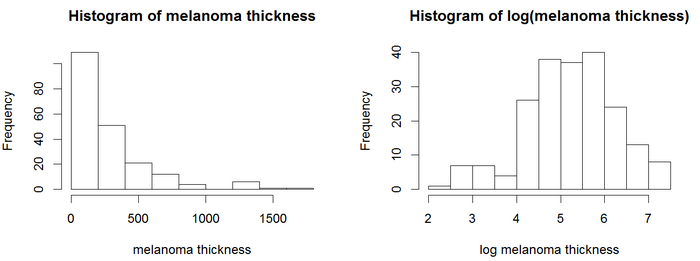
히스토그램에서 두께 값은 정규 분포를 따르지 않습니다.Cox 모형을 비롯한 회귀 모형은 일반적으로 정규 분포 변수를 사용하여 보다 신뢰할 수 있는 결과를 제공합니다.이 예에서는 로그 변환을 사용합니다.종양의 두께에 대한 로그가 더 정규 분포를 따르는 것으로 보이므로 Cox 모델은 로그 두께를 사용합니다.Cox PH 분석은 결과를 상자에 표시합니다.

세 가지 전체 검정(우도, Wald 및 점수)의 p-값이 모두 유의하므로 모형이 유의하다는 것을 나타냅니다.log(cof)에 대한 p-값은 6.9e-07이며, 위험비 HR = exp(coef) = 2.18로 종양의 두께와 사망 위험 증가 사이에 강한 관계가 있음을 나타낸다.

반면 성별에 대한 p-값은 이제 p=0.088이다.위험비 HR = exp(cof) = 1.58이며 95% 신뢰 구간은 0.934 - 2.68입니다.HR에 대한 신뢰 구간에는 1이 포함되므로, 이러한 결과는 성별이 종양의 두께를 조절한 후 HR의 차이에 더 적은 기여를 하고 유의성만을 지향한다는 것을 나타냅니다.성별에 따른 통나무(두께) 그래프와 성별에 따른 통나무(두께) t-검사는 모두 임상의를 처음 봤을 때 남녀 간에 종양의 두께에 유의한 차이가 있음을 나타낸다.

Cox 모형은 위험이 비례한다고 가정한다.비례 위험 가정은 R 함수 cox.zph()를 사용하여 시험할 수 있다.p-값이 0.05보다 작으면 위험이 비례하지 않음을 나타냅니다.흑색종 데이터의 경우 p=0.222, 위험이 최소한 근사적으로 비례함을 나타냅니다.Cox 모델을 검사하기 위한 추가 테스트와 그래프는 인용된 교과서에 설명되어 있습니다.

Cox 모델의 확장

Cox 모델을 확장하여 단순 분석의 변동을 처리할 수 있습니다.

• 계층화.피험자는 지층으로 나눌 수 있으며, 지층 내의 피험자는 다른 지층에서 무작위로 선택된 피험자보다 서로 상대적으로 더 유사할 것으로 예상된다.회귀 매개변수는 지층 전체에서 동일한 것으로 가정하지만 각 지층에 대해 다른 기준선 위험이 존재할 수 있다.계층화는 일치하는 피험자를 사용한 분석, 다른 클리닉과 같은 환자 하위 세트를 다루고 비례 위험 가정 위반을 처리하는 데 유용하다.
• 시간에 따라 변하는 공변량입니다.성별 및 치료 그룹과 같은 일부 변수는 임상 시험에서 일반적으로 동일하게 유지됩니다.혈청 단백질 농도 또는 동반 약물 복용량과 같은 다른 임상 변수는 연구 과정에서 변경될 수 있습니다.이러한 시간 가변 공변량에 대해 Cox 모델을 확장할 수 있습니다.

나무 구조 생존 모델

Cox PH 회귀 모형은 선형 모형입니다.선형 회귀 분석 및 로지스틱 회귀 분석과 유사합니다.특히 이러한 방법에서는 단일 선, 곡선, 평면 또는 표면이 그룹을 분리하거나(생존, 사망) 정량적 반응(생존 시간)을 추정하기에 충분하다고 가정합니다.

경우에 따라서는 대체 파티션이 더 정확한 분류 또는 정량적 추정치를 제공합니다.대안 방법 중 하나는 생존 랜덤 ^[6]포레스트를 포함한 나무 구조 생존 ^[3][4][5]모델이다.나무 구조 생존 모형은 Cox 모형보다 더 정확한 예측을 제공할 수 있습니다.주어진 데이터 세트에 대해 두 가지 유형의 모형을 모두 검사하는 것이 합리적인 전략입니다.

생존 트리 분석 예제

이 생존 트리 분석 예에서는 R 패키지 "rpart"^[7]를 사용합니다.이 예는 rpart의 데이터 세트 c 단계에서 146기 C 전립선암 환자를 기반으로 한다.Rpart와 Stagec 예는 Rpart ^[7]패키지의 vignette로 배포되는 Atkinson과 Therneau(1997)^[8]에 설명되어 있다.

단계별 변수는 다음과 같습니다.

• pgtime: 진행 시간 또는 진행 없는 마지막 후속 조치
• pgstat: 마지막 폴로업 상태(1=필수, 0=필수)
• 연령: 진단 시 연령
• et: 초기 내분비 치료(1=아니오, 0=예)
• 배합체: 이배체/사배체/무배체 DNA 패턴
• g2: G2상 셀의 %
• 등급: 종양 등급(1-4)
• 글리슨: 글리슨 등급(3-10)

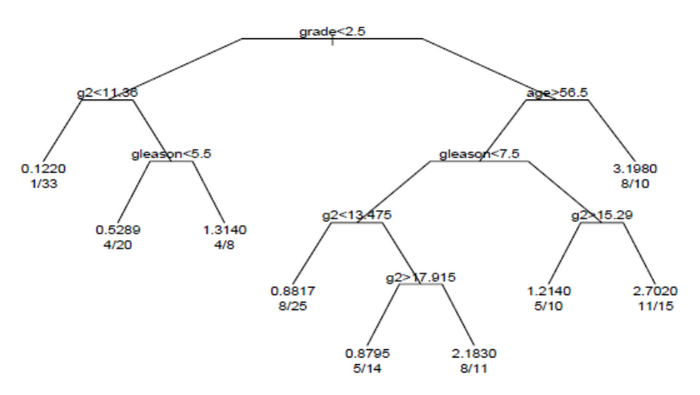
분석에 의해 생성된 생존 나무는 그림에 나와 있습니다.

트리의 각 분기는 변수 값에 대한 분할을 나타냅니다.예를 들어, 트리의 뿌리는 등급이 2.5 미만인 피험자와 등급이 2.5 이상인 피험자를 나눕니다.터미널 노드는 노드 내의 서브젝트 수, 이벤트가 있는 서브젝트 수 및 루트와 비교한 상대 이벤트환율을 나타냅니다.맨 왼쪽에 있는 노드에서 값 1/33은 노드 내의 33개 대상 중 하나에 이벤트가 있으며 상대 이벤트 비율이 0.122임을 나타냅니다.맨 오른쪽 하단에 있는 노드에서는 값 11/15가 노드 내의 15개 피험자 중 11개가 이벤트가 발생했음을 나타내며 상대 이벤트율은 2.7입니다.

생존 랜덤 포레스트

단일 생존 트리를 만드는 대안으로 데이터의 표본을 사용하여 각 트리를 구성하는 여러 생존 트리를 만들고 생존을 ^[6]예측하기 위해 나무의 평균을 내는 방법이 있습니다.이것은 생존 랜덤 포레스트 모델의 기초가 되는 방법입니다.생존 랜덤 포레스트 분석은 R 패키지 "random"에서 사용할 수 있습니다.Forest SRC"^[9]를 참조해 주세요.

랜덤ForestSRC 패키지에는 데이터 세트 pbc를 사용한 생존 랜덤 포레스트 분석 예가 포함되어 있습니다.이 데이터는 1974년과 1984년 사이에 수행된 간의 Mayo Clinic Primary 담도 간경화(PBC) 시험에서 나온 것이다.예제에서 랜덤 숲 생존 모형은 Cox PH 모형보다 더 정확한 생존 예측을 제공합니다.예측 오류는 부트스트랩 재샘플링을 통해 추정됩니다.

일반 제제

이 섹션은 어떠한 출처도 인용하지 않습니다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 섹션의 개선에 도움을 주십시오. 소스되지 않은 소재는 이의를 제기하여 삭제할 수 있습니다. (2021년 4월) (이 템플릿메시지를 삭제하는 방법과 타이밍에 대해 설명합니다)

서바이벌

주된 관심의 대상은 S로 일반적으로 표현되는 생존 함수이며, 다음과 같이 정의된다.

$\displaystyle S(t)=\Pr(T>t)}$

여기서 t는 약간의 시간, T는 사망 시간을 나타내는 랜덤 변수, "Pr"은 확률을 나타냅니다.즉, 생존 함수는 사망 시간이 특정 시간 t보다 늦을 확률입니다.생존함수는 생물학적 생존문제에서는 생존함수 또는 생존함수, 기계적 생존문제에서는 신뢰성함수라고도 불린다.후자의 경우 신뢰성 함수는 R(t)로 표기된다.

일반적으로 S(0) = 1로 가정하지만, 즉시 사망하거나 실패할 가능성이 있는 경우에는 1보다 작을 수 있다.

생존 함수는 증가하지 않아야 합니다. u t t인 경우 S(u) s S(t)입니다.T>u는 T>t를 의미하기 때문에 이 속성은 직접 이어집니다.이것은 모든 젊은 연령이 달성되어야만 만년 생존이 가능하다는 개념을 반영한다.이 속성을 지정하면 수명 분포 함수와 이벤트 밀도(아래 F 및 f)가 명확하게 정의됩니다.

생존 함수는 영생이 가능한 경우 한계가 0보다 클 수 있지만, 일반적으로 한계 없이 나이가 증가함에 따라 0에 근접하는 것으로 가정한다(즉, S(t) → 0을 t → δ).예를 들어, 우리는 안정적이고 불안정한 탄소 동위원소의 혼합물에 생존 분석을 적용할 수 있다. 불안정한 동위원소는 조만간 붕괴할 것이지만, 안정 동위원소는 무기한 지속될 것이다.

수명 분포 함수 및 이벤트 밀도

관련 수량은 생존 함수의 관점에서 정의된다.

일반적으로 F로 표기되는 수명 분포 함수는 생존 함수의 보완으로 정의된다.

$\displaystyle F(t)=\Pr(T\leq t)=1-S(t)}$

F가 미분 가능한 경우, 수명 분포의 밀도 함수인 도함수는 일반적으로 f로 표시된다.

${\displaystyle f(t)=F'(t)=flac {d}{dt}}F(t)}$

함수 f는 이벤트 밀도라고도 불리며 단위 시간당 사망 또는 고장 이벤트 비율입니다.

생존함수는 확률분포와 확률밀도함수로 표현될 수 있다.

$\displaystyle S(t)=\Pr(T>t)=\int _{t}^{\infty}f(u),du=1-F(t)}$

마찬가지로, 생존 이벤트 밀도 함수는 다음과 같이 정의할 수 있다.

${{displaystyle s(t)=S'(t)=snap frac {d}{dt}}\int _{t}^{\infty}f(u),du=nap frac {d}{dt}=[1-F(t)=f(t)]}$

통계물리학과 같은 다른 분야에서는 생존 이벤트 밀도 함수를 첫 번째 통과 시간 밀도로 알려져 있습니다.

위험 함수 및 누적 위험 함수

$통상적$으로 \$displaystyle \lambda$또는$$ $h\backslash$$displaystyle$h로 표기되는 위험함수는 $시간{\displaystyle }$ t$\displaystyle$t 이후$$($즉{\displaystyle }$, 시간 $\displaystyle$ T$\geq$t)$$까지의 생존을 조건으로$$ $시간{\displaystyle }$ t$\displaystyle$t의 이벤트 레이트로 정의됩니다.$아이템$이 1시간 $동안$ 존속했다고 가정합니다$.$또한 아이템이$1시간$ 이상 존속하지 않을 가능성이 있습니다$.$

${\displaystyle \sqda (t)=\lim _{dt\rightarrow 0}{\frac {Pr(t\leq T<t+dt}}}{dt\cdot S(t)}}={S(t)}{-{\frac {S'S(t)}{T}}}{t}}}$

사망력은 특히 인구통계학 및 보험수리학에서 사용되는 위험 함수의 동의어이며, 여기서$$μ ${\displaystyle$ \mu $\}$로 표시된다. 위험률이라는 용어는 또 다른 동의어이다.

생존 함수의 사망력은${\displaystyle }$μ (${\displaystyle x}$ ) ${\displaystyle =}$ - ${\displaystyle \frac{d}{}}$ d ${\displaystyle x\frac{}{}}$ ln${\displaystyle \delta }$ (${\displaystyle }$S (${\displaystyle x}$) ${\displaystyle =\frac{}{}f\frac{}{}}$ (${\displaystyle \frac{x}{}}$ )${\displaystyle \frac{}{}}$ (${\displaystyle \frac{x}{}}$) { $displaystyle \mux =$ - {$d$ \$over$ dx }\$ln ( S$ ( s ( x ) =$frac${ $f ($ x ) {$s$ ( x )}$$} 로 $정의$된다.

사망력은 실패력이라고도 합니다.사망률 분포의 확률 밀도 함수입니다.

보험수리학에서 위험률은 x$(\displaystyle$x$)$의 사망률입니다$.$ x(\$displaystyle$ x$)$의 경우, 수년 후의 $사망률$은 $t(\$$displaystyle$$t$의 사망률입니다.위험률은 고장률이라고도 합니다.위험률과 고장률은 신뢰성 이론에서 사용되는 이름입니다.

$함수$h는$다음$과 같은 특성을 만족하는 경우에만 위험 함수입니다.

1. ${\displaystyle x}$ x${\displaystyle 0}$ ${\displaystyle 0}$(${\displaystyle }$x ${\displaystyle )\ge }$ $0 ){$ $displaystyle$ \ $forall x$ \ $geq 0$\ $left$( h ($x$ ) \ $geq$0 \$$right $$${\displaystyle \mathrm{\}}}$ ,
2. ${\displaystyle {}_{}^{}\infty }$ ${\displaystyle 0{\mathrm{}}_{}^{}}$∞${\displaystyle h}$ ( ${\displaystyle x}$ ) d x$=$ \$displaystyle$ \$int _$ {0$}^{\infty }h(x$) display=\$infty$}.$$

실제로 위험률은 일반적으로 수명 분포의 다른 표현보다 기능 상실 메커니즘에 대해 더 많은 정보를 제공한다.

위험 함수는 음이 아니어야 합니다.${\displaystyle \mathrm{t}}$( t${\displaystyle }$) ${\$ 0 { $displaystyle$ \$lambda$ ($t$ ) \ $geq$ 0$$}$[{\displaystyle \mathrm{over}}$ over over over over over over over over [ over over over over over over over over over over,,0${\displaystyle }$,$displaystyle$ [$0$ , \ $infty ]$는 무한해야 합니다.다른 제약이 없습니다.증감하지 않거나 비단일 수 있습니다.예를 들어, 욕조 곡선 위험 함수는 t$\displaystyle$t의 $작은{\displaystyle }$ 값에 대해 큰 값으로 감소했다가 다시 증가하며, 이는 일부 기계 시스템의 특성을 작동 직후에 또는 시스템이 노후화됨에 따라 고장 나도록 모델링할 수 있습니다.

위험함수는 누적 위험함수(통례적으로 $denoted{\displaystyle \mathrm{}}${ $displaystyle$\ $Lambda$} $또는$ H { $displaystyle$ H$\})$로 나타낼 수 있다.

$\displaystyle \,\Lambda(t)=-\log S(t)}$

그래서 부호를 바꾸고 지수를 곱하면

$\displaystyle \,S(t)=\exp(-\Lambda(t))}$

또는 (체인 규칙에 따라) 구별합니다.

${\displaystyle\frac {d}{dt}\Lambda(t)=-{\frac {S'(t)}{S(t)}=\lambda(t)}.}$

"누적 위험 함수"라는 이름은 다음과 같은 사실에서 유래했다.

${\displaystyle \Lambda (t)=\int _{0}^{t}\displayda (u),du}$

시간 경과에 따른 위험의 "조절"이다.

$\delta {\displaystyle \mathrm{}}$( ${\displaystyle t}$) \ $displaystyle$\$Lambda$ $($$t$ )의 정의에서 t가 무한대에 가까워질수록 (S${\displaystyle }$(${\displaystyle t}$) \ $displaystyle$ S$(t)$가 0에 가까워지는 경향이 있다고 가정하면) 경계 없이 증가하는 것을 알 수 있습니다.이는 누적 위험이 정의상 분산되어야 하므로${\displaystyle }\delta {\displaystyle }$ (${\displaystyle t}$) {$style \lambda$($t)}$가 너무 빨리 감소해서는 안 된다는 것을 의미한다.예를 들어 exp ${\displaystyle (}$( -${\displaystyle t}$ $){$ $displaystyle \exp(-t)}$는 적분이 1로 수렴되기 때문에 생존 분포의 위험 함수가 아닙니다.

$(\displaystyle$$$S$(t$ 누적위험함수$δ(t$ $밀도{\displaystyle }$ f$t)$ {$f($$t$$),$ 위험함수${\displaystyle }$$\delta {\displaystyle }$($t$)${\displaystyle }$및$$수명배분함수 F$t)$는 style$$F(t)이다$.$

${\displaystyle S(t)=\exp[-\Lambda(t)]=sec frac {f(t)}{\displayda(t)}}=1-F(t),\quad t>0.}$

생존 분포에서 도출된 수량

특정 ${\displaystyle {시간\mathrm{}}_{}}$ ${\displaystyle {t\mathrm{}}_{}}$0({$display style t_{$0$$})의 미래 수명은 0$({$ style $t_{0$까지 생존할 경우 사망할 때까지 남은 시간입니다.따라서 현재 표기법으로는 T${\displaystyle }$- ${\displaystyle {t\mathrm{}}_{}}$0 { $displaystyle$ T - $t$_ { $0$} 입니다.예상되는 미래 라이프 타임은 미래 라이프 타임의 기대치입니다.${\displaystyle {0세}_{}}$까지 생존할 경우 ${\displaystyle {t\mathrm{}}_{}\mathrm{0세}}$+ t {\$displaystyle t_{$0$\}+$$t$에 사망할 확률은 매우 낮다$.$

${\displaystyle P(T\leq t_{0}+mid T>t_{0})=param frac {P(t_{0}<T\leq t_{0}}}{P(T>t_{0}}}}=param frac {F(T_{0})-{0}}$

따라서, 미래 수명의 확률 밀도는

${\displaystyle {frac {d} {\frac {F(t_{0}+t}-F(t_{0})} {S(t_{0}}}} = specfrac {f(t_{0}+t)} {\frac}S(t_{0}}}}}:}$

그리고 미래의 예상 라이프 사이클은

${\displaystyle {1}{S(t_{0}}}\int _{0}^{\infty }t,f(t_{0}+t),dt=param frac {1}{S(t_{0}}}}\int _{\infty }S(t)S,t,t,t}$

부품별 적분을 사용하여 두 번째 식을 얻을 수 있습니다.

${\displaystyle {t\mathrm{}}_{}}$ 0 ${\displaystyle {}_{}}$ { $displaystyle t$_ { 0 } $= 0$, 、 즉, 출생 시 기대 수명까지 감소합니다.

신뢰성 문제에서 기대수명은 평균수명이라고 불리며, 예상미래수명은 평균잔존수명이라고 불립니다.

개인이 t세 이상까지 생존할 확률은 S(t)이므로, 정의상 n명의 신생아 초기 모집단 중 t세 생존자의 예상 수는 n × S(t)이며, 모든 개인에 대해 동일한 생존 기능을 가정한다.따라서 생존자의 예상 비율은 S(t)이다.다른 개체들의 생존이 독립적일 경우, t세 생존자 수는 매개변수 n과 S(t)를 갖는 이항 분포를 가지며 생존자 비율의 분산은 S(t) × (1-S(t)/n이다.

생존자의 특정 비율이 남아 있는 나이는 방정식 S(t) = q for t를 풀면 알 수 있다. 여기서 q는 문제의 분위수이다.일반적으로 q = 1/2인 중위수 수명 또는 q = 0.90 또는 q = 0.99와 같은 다른 분위수에 관심이 있습니다.

검열

관측 중단은 모집된 모든 피험자가 관심 사건을 보여주거나 피험자가 사건을 경험하기 전에 연구를 종료하기 전에 사건 발생까지의 시간이 관찰되지 않는 결측 데이터 문제의 한 형태입니다.관측 중단은 생존 분석에서 일반적입니다.

실제 사건 시간 T의 하한 l만 T > l로 알려진 경우 이를 우측 관측 중단이라고 합니다.예를 들어, 생년월일이 알려져 있지만 추적 관찰로 상실되거나 연구가 종료될 때 아직 살아있는 피실험자에 대해 우측 중도 절단이 발생합니다.일반적으로 우측 관측 중단 데이터를 접하게 됩니다.

관심 사건이 연구에 포함되기 전에 이미 발생했지만 언제 발생했는지 알 수 없는 경우 데이터는 좌측 중도 ^[10]절단된 것으로 간주됩니다.두 관측치 또는 검사 사이에 사건이 발생했다고만 말할 수 있는 경우 구간 관측 중단입니다.

예를 들어, 왼쪽 중도 절단은 영구치의 출현 분포를 추정하는 치과 연구를 시작하기 전에 영구치가 이미 출현한 경우에 발생합니다.같은 연구에서는 현재 검사에서는 영구치가 입안에 있지만 이전 검사에서는 영구치가 없는 경우 발생 시간을 간격 검열합니다.HIV/AIDS 연구에서 간격 검열이 종종 발생합니다.실제로 HIV 혈청전환 시간은 보통 내과 방문 후에 시작되는 실험실 평가에 의해서만 결정될 수 있다.그렇다면 두 검사 사이에 HIV 혈청전환이 일어났다는 결론만 내릴 수 있다.임상 증상에 근거해 건강검진을 실시해야 하는 에이즈의 진단도 마찬가지다.

또, 라이프 타임이 문턱값보다 작은 서브젝트가 전혀 관찰되지 않는 경우가 있습니다.이것은 잘라내기라고 불립니다.왼쪽 관측 중단 기준의 경우 주제가 존재하지만 잘린 기준의 경우 주제를 완전히 인식하지 못할 수 있으므로 잘라낸 것은 왼쪽 관측 중단과 다릅니다.잘라내는 것도 일반적입니다.이른바 지연진입연구에서 피험자는 특정 연령이 될 때까지 관찰되지 않는다.예를 들어, 사람들은 학교에 들어갈 나이가 될 때까지 관찰되지 않을 수 있다.취학 전 연령대에서 사망한 피험자는 알려지지 않았을 것이다.왼쪽 잘라낸 데이터는 생명보험과 ^[11]연금에 대한 보험수리적 작업에서 흔히 볼 수 있다.

좌측 검열 데이터는 추적 기간 중 좌측에 생존 시간이 불완전해지면 발생할 수 있습니다.예를 들어, 역학적인 예에서는 감염 검사에서 양성 반응이 나온 시점부터 감염성 질환 여부를 관찰할 수 있습니다.관심 기간의 오른쪽은 알 수 있지만,^[12] 감염원에 대한 정확한 노출 시간은 알 수 없을 수도 있습니다.

데이터에 매개 변수 적합

생존 모형은 반응 변수가 시간인 일반 회귀 모형으로 유용하게 볼 수 있습니다.그러나 관측 중단으로 인해 (모수를 적합하거나 다른 종류의 추론을 수행하는 데 필요한) 우도 함수를 계산하는 것이 복잡합니다.관측 중단 데이터가 있는 경우 생존 모형에 대한 우도 함수는 다음과 같이 공식화됩니다.정의상 우도 함수는 모형의 모수가 주어진 데이터의 조건부 확률입니다.모수가 주어지면 데이터가 독립적이라고 가정하는 것이 일반적입니다.그런 다음 우도 함수는 각 기준점의 우도의 곱입니다.데이터를 비절단, 왼쪽 관측 중단, 오른쪽 관측 중단 및 구간 관측 중단의 네 가지 범주로 분할하는 것이 편리합니다.아래 식에서는 "unc", "l.c.", "r.c.", "i.c."로 표기됩니다.

$\displaystyle L(\theta)=\display_{T_{i}\in unc.}\Pr(T=T_{i}\mid \theta)\pr(T<T_{i}\mid \theta)\pr(T>T_{i}\mid \theta)_{i}\pr(T)\pr(i\in l.c.}\pr.\pr.}$

검열되지 않은 데이터의 경우,$Ti$(\displaystyle $T_{i})$가 사망 시 연령과 같으면

$\Displaystyle \Pr(T=T_{i}\mid \theta)=f(T_{i}\mid \theta).}$

사망 연령이 $(\$ $미만$인 왼쪽 검열 데이터의 경우,

$\Displaystyle \Pr(T<T_{i}\mid \theta)=F(T_{i}\mid \theta)=1-S(T_{i}\mid \theta).}$

사망 연령이 $(\$보다 높은 우측 검열 데이터의 경우,

$\displaystyle \Pr(T>T_{i}\mid \theta)=1-F(T_{i}\mid \theta)=S(T_{i}\mid \theta).}$

사망시 연령이 ${\displaystyle {Ti,}_{}}$ $\$보다 작고 ${\displaystyle {Ti,}_{}}$ $\$보다 큰 것으로 알려진 간격 관측 중단 기준의 경우, 다음과 같이 합니다.

$\Displaystyle \Pr(T_{i,l}\mid \theta)=S(T_{i,l}\mid \theta)-S(T_{i,r}\mid \theta)}$

인터벌 검열 데이터가 발생하는 중요한 애플리케이션은 현재 상태 데이터이며, 여기서 $이벤트{\displaystyle {}_{}}$ $(\$})는$$ 관측 시간 이전에 발생한 것이 아니라 다음 관측 시간 이전에 발생한 것으로 알려져 있습니다.

비모수 추정

카플란-마이어 추정기를 사용하여 생존 함수를 추정할 수 있습니다.Nelson-Aalen 추정기를 사용하여 누적 위험률 함수의 비모수 추정치를 제공할 수 있다.

생존 분석용 컴퓨터 소프트웨어

Kleinbaum의 교과서에는 SAS, ^[13]R 및 기타 패키지를 사용한 생존 분석의 예가 있다.Brostrom,^[14] Dalgaard^[2], Tableman과^[15] Kim의 교과서에는 R(또는 S를 사용하고 R로 실행되는)을 사용한 생존 분석의 예가 나와 있습니다.

생존 분석에 사용되는 분포

• 지수 분포
• 와이불 분포
• 로그 로지스틱 분포
• 감마 분포
• 지수-대수
• 일반화 감마 분포

적용들

• 신용위험^[16][17]
• 사형을^[18] 선고받은 수감자의 허위 유죄판결율
• 항공우주산업^[19] 금속부품 리드타임
• 범죄^[20] 재범에 대한 예측자
• 무선 태그 부착 동물의^[21] 생존 분포
• 로마^[22] 황제들의 폭력적 죽음

「 」를 참조해 주세요.

레퍼런스

추가 정보

• Collett, David (2003). Modelling Survival Data in Medical Research (Second ed.). Boca Raton: Chapman & Hall/CRC. ISBN 1584883251.
• Elandt-Johnson, Regina; Johnson, Norman (1999). Survival Models and Data Analysis. New York: John Wiley & Sons. ISBN 0471349925.
• Kalbfleisch, J. D.; Prentice, Ross L. (2002). The statistical analysis of failure time data. New York: John Wiley & Sons. ISBN 047136357X.
• Lawless, Jerald F. (2003). Statistical Models and Methods for Lifetime Data (2nd ed.). Hoboken: John Wiley and Sons. ISBN 0471372153.
• Rausand, M.; Hoyland, A. (2004). System Reliability Theory: Models, Statistical Methods, and Applications. Hoboken: John Wiley & Sons. ISBN 047147133X.

외부 링크

• Therneau, Terry. "A Package for Survival Analysis in S". Archived from the original on 2006-09-07. Dr.를 경유하여 Mayo Clinic 웹사이트 Therneau's 페이지
• "Engineering Statistics Handbook". NIST/SEMATEK.
• 소크라테스, 생존 분석 애플릿 및 대화형 학습 활동.
• 생존/수명 분석 @ 통계' 교과서 페이지
• R에서의 생존 분석
• 생존 분석을 위한 Python 패키지인 Lifelines
• NAG Fortran 라이브러리의 생존 해석