효과 크기

이 문서에는 여러 가지 문제가 있습니다.개선을 돕거나 토크 페이지에서 이러한 문제에 대해 논의해 주십시오.(이러한 템플릿메시지를 삭제하는 방법과 타이밍에 대해 설명합니다) 이 문서는 Wikipedia의 품질 기준을 충족하기 위해 청소가 필요할 수 있습니다.구체적인 문제는 수학 표기법은 다른 기호를 사용하여 유사한 공식에서 동일한 양을 나타낸다는 것입니다. 가능하면 이 문서의 개선에 협조해 주십시오. (2011년 5월) (이 템플릿메시지 삭제 방법 및 삭제 타이밍에 대해 알아보기) 이 기사는 대부분의 독자들이 이해하기에는 너무 전문적일 수 있다. 기술적인 세부사항을 삭제하지 않고 비전문가도 쉽게 이해할 수 있도록 개선해 주십시오. (2014년 2월) (이 템플릿메시지 삭제 방법 및 삭제 시기 확인) (이 템플릿메시지를 삭제하는 방법과 타이밍을 확인합니다)

통계학에서 효과 크기는 모집단의 두 변수 간 관계의 강도를 측정하는 값 또는 해당 수량의 표본 기반 추정치입니다.데이터 표본에서 계산된 통계 값, 가상 모집단에 대한 모수 값 또는 통계 또는 모수가 효과 크기 ^[1]값으로 이어지는 방법을 연산하는 방정식을 참조할 수 있습니다.효과 크기의 예로는 두 ^[2]변수 간의 상관 관계, 회귀에서의 회귀 계수, 평균 차이 또는 특정 사건(심장 마비와 같은) 발생 위험이 있습니다.효과 크기는 통계 가설 테스트를 보완하고 전력 분석, 표본 크기 계획 및 메타 분석에서 중요한 역할을 한다.효과 크기에 대한 데이터 분석 방법의 군집을 추정 통계량이라고 합니다.

효과 크기는 통계 클레임의 강도를 평가할 때 필수적인 요소이며, MAGIC 기준의 첫 번째 항목(크기)이다.효과 크기의 표준 편차는 측정에 포함되는 불확실성의 정도를 나타내기 때문에 매우 중요하다.표준 편차가 너무 크면 측정이 거의 무의미해집니다.다중 효과 크기를 결합하는 것이 목적인 메타 분석에서는 효과 크기의 불확실성을 사용하여 효과 크기를 측정하므로 소규모 연구보다 대규모 연구가 더 중요한 것으로 간주된다.효과 크기의 불확실성은 효과 크기 유형에 따라 다르게 계산되지만 일반적으로 연구의 표본 크기(N) 또는 각 그룹의 관측치 수(n)만 알면 된다.

많은 ^[3][4]분야에서 경험적 연구 결과를 제시할 때 효과 크기 또는 그 추정치(효과 추정치[EE], 효과 추정치)는 모범 사례로 간주된다.효과 크기의 보고는 통계적 ^[5]의미와 대조적으로 연구 결과의 중요성에 대한 해석을 용이하게 한다.효과 크기는 사회과학 및 의학 연구(치료 효과의 크기가 중요한 경우)에서 특히 두드러진다.

효과 크기는 상대 또는 절대 단위로 측정할 수 있습니다.상대적 효과 크기에서는 승산비 및 상대적 위험과 같이 두 그룹이 서로 직접 비교된다.절대 효과 크기의 경우 절대값이 클수록 항상 더 강한 효과를 나타냅니다.많은 유형의 측정이 절대 또는 상대 측정으로 표현될 수 있으며, 서로 다른 정보를 전달하기 때문에 함께 사용할 수 있습니다.심리학 연구 커뮤니티의 저명한 태스크 포스는 다음과 같은 권고를 했다.

항상 주요 결과에 대한 효과 크기 표시...측정 단위가 실제 수준(예: 하루 흡연 담배 수)에서 의미가 있는 경우, 우리는 일반적으로 표준화된 측정(r 또는 d)^[3]보다 표준화되지 않은 측정(회귀 계수 또는 평균 차이)을 선호한다.

개요

모집단 및 표본 효과 크기

통계적 추정에서와 같이, 실제 효과 크기는 관측된 효과 크기와 구별된다. 예를 들어 모집단(모임 효과 크기)의 질병 위험을 측정하기 위해 해당 모집단(표본 효과 크기)의 표본 내에서 위험을 측정할 수 있다.참 및 관측된 효과 크기를 기술하는 규칙은 표준 통계 관행을 따른다. 한 가지 일반적인 접근법은 모집단 매개변수를 나타내기 위해 그리스 문자를 사용하고 해당 통계를 나타내기 위해 r과 같은 라틴 문자를 사용하는 것이다.또는 모집단 파라미터 위에 "모자"를 배치하여 통계를 나타낼 수 있습니다. $예$를 들어, $^$ ${\$$display\hot$는 $파라미터$의 추정치입니다$.$

모든 통계 설정과 마찬가지로 효과 크기는 표본 오차로 추정되며, 사용되는 효과 크기 추정기가 데이터가 표본 추출된 방법 및 측정이 수행된 방법에 적절하지 않은 한 편향될 수 있다.이것의 예는 출판 편향이다. 이것은 과학자들이 추정 효과 크기가 크거나 통계적으로 유의한 경우에만 결과를 보고할 때 발생한다.그 결과, 많은 연구자가 낮은 통계력으로 연구를 수행하는 경우 보고된 효과 크기는 실제(모집단) 효과보다 더 큰 경향이 있습니다.^[6]효과 크기가 왜곡될 수 있는 또 다른 예는 다중 시험 실험에서 효과 크기 계산은 ^[7]시험 전체의 평균 또는 집계 반응에 기초한다.

소규모 연구는 대규모 연구와 다른 효과 크기를 나타내기도 합니다.이 현상은 소규모 연구 효과로 알려져 있으며, 이는 출판 ^[8]편향의 신호일 수 있다.

검정 통계와의 관계

표본 기반 효과 크기는 관찰된 관계의 크기가 우연에 의한 것일 수 있는지 여부를 반영하는 유의 수준을 할당하는 대신 예를 들어 명백한 관계의 강도(크기)를 추정한다는 점에서 가설 테스트에 사용된 테스트 통계와 구별된다.효과 크기는 유의 수준을 직접 결정하지 않으며, 그 반대도 마찬가지입니다.표본 크기가 충분히 클 경우, 모집단 효과 크기가 정확히 0이 아닌 한(그리고 사용된 유형 I 오류의 비율로 통계적 유의성을 나타냄) 비늘 통계적 비교는 항상 통계적으로 유의한 결과를 보여준다.예를 들어 표본 크기가 1000이면 표본 Pearson 상관 계수가 0.01이면 통계적으로 유의합니다.0.01의 상관 관계가 너무 작아서 특정 응용 프로그램에 관심이 없을 경우 이 분석의 유의한 p-값만 보고하면 오해의 소지가 있습니다.

표준화된 효과 크기 및 표준화되지 않은 효과 크기

용어 효과 크기는 표준화된 효과 측정값(예: r, Cohen의 d 또는 승산비) 또는 표준화되지 않은 측정값(예: 그룹 평균 간의 차이 또는 표준화되지 않은 회귀 계수)을 나타낼 수 있습니다.표준화된 효과 크기 측정은 일반적으로 다음과 같은 경우에 사용된다.

• 연구 대상 변수의 메트릭은 본질적인 의미를 가지지 않는다(예: 임의의 척도의 인성 테스트 점수).
• 여러 연구에서 나온 결과들이 합쳐지고 있습니다.
• 일부 또는 모든 스터디가 다른 척도를 사용합니다.
• 모집단의 변동성과 관련된 효과의 크기를 전달하는 것이 바람직하다.

메타 분석에서 표준화된 효과 크기는 다른 연구에 대해 계산될 수 있는 일반적인 척도로 사용되고 전체 요약으로 결합된다.

해석

효과 크기 소형, 중형, 또는 그 실질적인 컨텍스트 및 운용 정의에 커다란 질량으로 해석되어야 한다.코헨의 재래식 기준, 중간 것, 비록 Cohen[9]다고 경고했다 big[9] 많은 들판을 가로지르는 유비쿼터스 근처에 있는데, 작은.

"조건은 'small,의 'medium,'와 'large 있어요 '라고 상대, 그저 서롰지만 그 지역의 행동 과학이나 심지어 좀 더 특별하기 위해 그 특정한 콘텐츠와 연구 방법이 있는 것 고용된 어떤 정해진 조사....이 상대성 이론의 얼굴에는 약간은 위험한 조건을 위해 권력을 분석 조산 다양한 분야에서 행동 과학으로서의 사용으로 기존의 운영상의 정의는 제공하는 내재해 있다.이러한 위험은 그럼에도 불구하고 그 믿음에 이상이 기준 때만 배아 줄기 지수를 평가하는 더 나은 기반이 되는 것은available."(페이지의 주 25)사용하기 위해 권고한 일반적인 재래식 프레임 공급에 의해 잃는 것을 얻을 수 있다. 인정된다.

두 샘플 레이아웃에서 Sawilowsky[10]마음 속에 코헨의 주의하고, 그 설명은 매우 작고, 아주 그리고 큰 큰 포함하게"현재 연구 결과는 적용된 문학에 기초하여, 그것은 엄지 손가락의 효과 크기에 대한 규칙을 개정하는 것은 적절한 것 같다."결론을 내렸다.그 같은 사실상의 표준 다른 레이아웃을 위해 개발될 수 있다.

Lenth[11]는"매체"효과 크기에 대해 당신은 상관 없이 악기 또는 학과들의 의사를 또는 다양성의 정확성 또는 신뢰성의 같은 n를 선택해 드린다고 말했다.분명히, 중요한 고려 사항들 여기서 무시되고 있다.연구자들이 의미 있는 정황에 접지나 지식에 대한 기여를 수량화에 의해서 코헨의 효과 크기에 대한 설명은 출발점으로서 도움이 될 수 있어 그 결과의 실질적인 의미 해석해야 한다."[5]비슷하게, 미국 부 교육의 보고서 코헨의 제네릭 소형, 중형의 " 이러한 광범위한 무분별하고 큰 효과 크기 값이 그의 규범적 가치 적용되지 않는다 영역에서 효과 크기의 특징을 나타내는 것 따라서 마찬가지로 사실과 다르기는 부적절하다를 후원했다."[12]

그들은 "적절한 규범은 비교 가능한 표본을 대상으로 한 비교 가능한 개입의 비교 가능한 결과 측정에 대한 효과 크기 분포에 기초한 규범"이라고 제안했다.따라서 대부분의 개입이 작은 분야의 연구가 (코헨의 기준에 의해) 작은 효과를 가져온다면, 이러한 새로운 기준은 그것을 "대규모"라고 부를 것이다.이와 관련하여, 에벨슨의 역설과 사윌로스키의 ^[13][14][15]역설에 대해 살펴보자.

종류들

효과 크기에 대한 약 50 - 100개의 다른 측정이 알려져 있습니다.많은 경우 두 분포의 분리를 추정하므로 서로 다른 유형의 많은 효과 크기를 다른 유형으로 변환할 수 있습니다. 따라서 수학적으로도 관련이 있습니다.예를 들어 상관계수를 Cohen의 d로 변환하거나 그 반대로 변환할 수 있습니다.

상관계: "설명된 분산"에 따른 효과 크기

이러한 효과 크기는 실험 모형에 의해 "설명"되거나 "설명된 변동"되는 실험 내 분산의 양을 추정합니다.

Pearson r 또는 상관 계수

종종 r로 표시되고 Karl Pearson에 의해 소개된 Pearson의 상관관계는 쌍체 정량 데이터를 사용할 수 있을 때 효과 크기로 널리 사용됩니다(예: 출생 체중과 수명 사이의 관계를 연구하는 경우).상관 계수는 데이터가 이항인 경우에도 사용할 수 있습니다.Pearson의 r은 -1부터 1까지 다양할 수 있으며 -1은 완벽한 음의 선형 관계를 나타내고 1은 완벽한 양의 선형 관계를 나타내며 0은 두 변수 사이에 선형 관계가 없음을 나타냅니다.Cohen은 사회과학에 ^[9][16]대해 다음과 같은 지침을 제공합니다.

효과 크기	r
작은.	0.10
중간의	0.30
큰.	0.50

결정계수(r² 또는² R)

관련된 효과 크기는 결정 계수인 r(R 또는 "r-제곱"이라고도² 함)이며², Pearson 상관 관계 r의 제곱으로 계산됩니다.쌍체 데이터의 경우 이 값은 두 변수가 공유하는 분산 비율을 나타내는 측도로 0에서 1까지 다양합니다.예를 들어, r이 0.21이면 결정 계수는 0.0441로, 두 변수의 분산 중 4.4%가 다른 변수와 공유됩니다.r은² 항상 양의 값이기 때문에 두 변수 간의 상관 관계 방향을 전달하지 않습니다.

에타² 제곱(θ)

Eta-제곱은 다른 예측 변수를 제어하는 동안 종속 변수에 의해 설명되는 분산의 비율을 나타내므로² r과 유사합니다. Eta-제곱은 모집단의 모형에 의해 설명되는 분산의 편향된 추정기입니다(표본의 효과 크기만 추정).이 추정치는 변수가 추가될 때마다 자동으로 η의² 값이 증가한다는 약점을 r과² 공유한다.또한 모집단이 아니라 표본에 설명된 분산을 측정합니다. 즉, 표본이 커질수록 치우침이 작아지지만 효과 크기를 항상 과대평가합니다.

${\displaystyle \eta ^{2}=black {SS_{\text{Treature}}}{SS_{\text{합계}}}}}}.}$

오메가² 제곱())

모집단에서 설명되는 분산의 덜 치우친 추정치는 다음과^2[17] 같습니다.

${\displaystyle \obega ^{2}=black {{\text}SS}_{\text{treature}}-df_{\text{treature}}\cdot{text{text}MS}_{\text{error}}{\text{SS}_{\text{total}}+{\text{MS}}_{\text{error}}}}.}$

이 공식의 형식은 모든 ^[17]셀에서 동일한 표본 크기를 가진 피실험자 간 분석으로 제한됩니다.(편향은 없지만) 편향이 적기 때문에 is보다는² is가² 바람직하지만 복잡한 분석의 경우 계산하기가 더 불편할 수 있다.일반화된 형태의 추정기는 피실험자 간 및 피실험자 내 분석, 반복 측정, 혼합 설계 및 랜덤화 블록 설계 ^[18]실험을 위해 발행되었습니다.또한 독립 변수가 최대 3개인 설계에서 개별 요인과 결합된 요인의 부분 θ를² 계산하는 방법도 발표되었다.^[18]

코헨의² »

Cohen의 is은² 분산 분석 또는 다중 회귀 분석에 대한 F-검정의 맥락에서 사용하는 여러 효과 크기 측도 중 하나입니다.편중량(분산 분석에 대한 효과 크기 추정)은 기초적인 분산 측정값(예: R, δ², δ²²)의 편중량에 따라 달라진다.

다중 회귀 분석의 δ² 효과 크기 측정은 다음과 같이 정의됩니다.

${\displaystyle f^{2}={R^{2}\over 1-R^{2}}$

여기서² R은 다중 상관의 제곱입니다.

마찬가지로 can은² 다음과 같이 정의할 수 있습니다.

${\displaystyle {f\mathrm{}}^{}}$ 2 ${\displaystyle {}^{}}$ ${\displaystyle \frac{{\eta \mathrm{}}^{}}{}}$ ${\displaystyle \frac{{}^{}}{\mathrm{}}}$1 - ${\displaystyle \frac{{2\mathrm{}}^{}}{}}$2 { \ $displaystyle f^$ { } =$over 1-\eta$^ {$}$ ${\displaystyle {fた}^{}}$ ${\displaystyle {}^{}}$ ${\displaystyle \frac{{2\mathrm{}}^{}}{}}$ ${\displaystyle \frac{{}^{}}{\mathrm{}}}$ 1${\displaystyle \frac{}{}}$- ${\displaystyle \frac{{\omega \mathrm{}}^{}}{}}$ 2$$\ $displaystyle$ f^ {2$} = omega$ 2 \ $over 1-\$ 메가 ^ {2$}$}

해당 효과 크기 ^[19]측정으로 설명된 모델의 경우.

${\displaystyle {f\mathrm{}}^{}}$ 2$(\$ f$^{2})$ 효과$$ 크기 측정은 $순차{\displaystyle {}^{}}$ 다중 회귀 분석 및 PLS 모델링에서^[20] 공통으로 사용됩니다.

${\displaystyle f^{2}={R_{AB}^{2}-R_{A}^{2} \over 1-R_{AB}^{2}}}$

여기서²_A R은 하나 이상의 독립 변수 A의 집합에 의해 설명되는 분산이고²_AB, R은 A와 다른 하나 이상의 관심 변수 B의 집합에 의해 설명되는 결합된 분산이다.관례상 0.$($.1$^{2$${\displaystyle {\mathrm{}}^{}}0$.$($0.$25^{2$ 및$.$42($디스플레이 스타일 0.4^{$2$$})의 $효과$ 사이즈는² 각각 소형,^[9] 중형, 대형이라고 한다.

Cohen의 f$^{${f$}}$은(는) 역방향으로 작동하는 요인 분석(ANOVA)에도 사용할 수 있습니다.

${\displaystyle {f}_{\text{effect}={(F_{\text{effect}}df_{\text{effect}/N}}}}}.}$

분산 분석의 균형 설계(그룹 간 동등한 표본 크기)에서 $(\$ f$^{2})$의 해당 모집단 매개변수는 다음과 같다.

${\displaystyle {SS(\mu _{1},\mu _{2},\dots,\mu _{K}} \over {K\times \sigma ^{2}}$

여기서_j μ는 총 K개 그룹의 j개^th 그룹 내 모집단 평균과 θ 각 그룹 내 등가 모집단 표준 편차를 나타낸다.제곱합은 분산 분석에서 제곱합입니다.

코헨의 Q

상관 차이에 사용되는 또 다른 척도는 Cohen의 q입니다.이 값은 두 Fisher 변환된 Pearson 회귀 계수 간의 차이입니다.기호에서 이것은

${\displaystyle q=sqrfrac {1}{1}\log {\frac {1}-{1}}-{1}{2}}-{log {\frac {1+r_{2}}{1-r_{2}}}}}$

여기서₁ r과₂ r은 비교되는 회귀입니다.q의 예상값은 0이고 분산은

${\displaystyle \operatorname {var}(q)=parfrac {1}{N_{1}-3}+{\frac {1}{N_{2}-3}}$

여기서₁ N과₂ N은 각각 첫 번째 및 두 번째 회귀 분석의 데이터 점 수입니다.

차이 제품군: 평균 간 차이에 따른 효과 크기

두 그룹의 비교와 관련된 원시 효과 크기는 본질적으로 두 평균 간의 차이로 계산됩니다.그러나 해석을 용이하게 하기 위해 효과 크기를 표준화하는 것이 일반적이다. 통계 표준화를 위한 다양한 관행이 아래에 제시되어 있다.

표준화된 평균 차이

평균에 기초한 (모집단) 효과 크기 θ는 일반적으로 두 모집단^{[21]: 78} 간의 표준화 평균 차이(SMD)를 고려합니다.

${\displaystyle \theta = prac {mu _{1}-\mu _{2}} {\display }$

여기서₁ μ는 한 모집단의 평균이고₂ μ는 다른 모집단의 평균이며 θ는 둘 중 하나 또는 둘 모두를 기준으로 하는 표준 편차입니다.

실제 설정에서는 일반적으로 모집단 값을 알 수 없으며 표본 통계량에서 추정해야 합니다.평균에 기반한 효과 크기의 여러 버전은 사용되는 통계량에 따라 다릅니다.

이 효과 크기 형식은 t 검정 통계량 계산과 유사하며 t 검정 통계량에는 n$(\displaystyle\sqrt {n$의 계수가 포함되어 있는 중요한 차이가 있습니다.즉, 주어진 효과 크기에 대해 유의 수준은 표본 크기에 따라 증가합니다.t-검정 통계량과 달리 효과 크기는 모집단 모수를 추정하는 것을 목적으로 하며 표본 크기에 영향을 받지 않습니다.

SMD 값 0.2~0.5는 작은 것으로 간주되며, 0.5~0.8은 중간으로 간주되며, 0.8보다 큰 ^[22]것은 큰 것으로 간주됩니다.

코헨의 d

Cohen의 d는 두 평균 간의 차이를 데이터에 대한 표준 편차로 나눈 값으로 정의됩니다.

${{displaystyle d=mar frac {\bar {x}}_{1}-{\bar {x}_{2}}{s}}.}$

Jacob Cohen은 합동 표준 편차인 s를 (두 개의 독립적인 표본에 대해)^{[9]: 67} 다음과 같이 정의했습니다.

${{displaystyle s=secrt {(n_{1}-1)s_{1}^{2}+(n_{2}-1)s_{2}}{n_{1}+n_{2}}}}$

여기서 그룹 중 하나에 대한 분산은 다음과 같이 정의됩니다.

${\displaystyle s_{1}^{2}=black {1}{n_{1}\sum _{i=1}^{n_1}(x_{1,i}-{\bar {x}_{1})^2}$

다른 그룹도 마찬가지입니다.

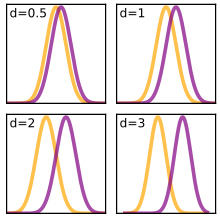
아래 표에는 코헨이 처음 제안하고 Sawilowsky가 ^[10]확장한 d = 0.01 ~ 2.0의 등급에 대한 설명자가 포함되어 있습니다.

효과 크기	d	언급
초소형	0.01	[10]
작은.	0.20	[9]
중간의	0.50	[9]
큰.	0.80	[9]
매우 크다	1.20	[10]
커다란	2.0	[10]

다른 저자들은 분모가 "-2"^{[23][24]: 14} 가 없는 "코헨 d"를 참조할 때 표준 편차의 약간 다른 계산을 선택한다.

${\displaystyle s=secrt {(n_{1}-1)s_{1}^{2}+(n_{2}-1)s_{2}{n_{1}+n_{2}{n_{1}}}}}}$

이러한 "코헨 d"의 정의는 Hedges와 ^[21]Olkin에 의해 최대우도 추정치라고 불리며, 스케일 팩터에 의해 Hedges의 g와 관련이 있다(아래 참조).

두 개의 쌍체 표본을 사용하여 차이 점수의 분포를 살펴봅니다.이 경우 s는 이 차이 점수 분포의 표준 편차입니다.따라서 두 그룹의 평균 차이를 검정하기 위한 t-통계량과 Cohen의 d 사이에 다음과 같은 관계가 생성됩니다.

${{displaystyle t=bar frac {\bar {X}}_{1}-{\bar {X}_{2}}{\text{\text}SE}} = flac {\bar {X}_{1}-{\bar {X}_{2}}{\frac {\text{\frac}SD}}{\sqrt {N}}}=sqrt {N}}({\bar {X}}_{1}-{\bar {X}_{2}})}}{SD}}}$

그리고.

${{displaystyle d=mar frac {\bar {X}}_{1}-{\bar {X}_{2}}{\text{\text}SD}}=syslogfrac {t}{\syslogrt {N}}}}$

Cohen의 d는 통계 검정을 위한 표본 크기를 추정하는 데 자주 사용됩니다.코헨의 d가 작을수록 표본 크기가 커지며, 그 반대의 경우도 원하는 유의 수준 및 통계적 ^[25]파워의 추가 매개변수와 함께 결정됩니다.

쌍으로 구성된 표본의 경우, 코헨은 계산된 d가 실제로 d'이며, 이는 테스트의 검정력을 얻기 위한 정답을 제공하지 않으며, 제공된 표에서 값을 찾기 전에 다음 ^[26]공식에서와 같이 r에 대해 보정해야 한다고 제안합니다.

${\displaystyle d=syslogfrac {d'}{\syslogrt {1-r}}}}$

유리' δ

1976년, 진 V. Glass는 두 번째^{[21]: 78} 그룹의 표준 편차만 사용하는 효과 크기의 추정기를 제안했습니다.

${{displaystyle\Delta={\bar {x}_{1}-{\bar {x}}_{2}}:{s_{2}}}}$

두 번째 그룹은 대조군으로 간주될 수 있으며, Glass는 여러 가지 처리를 대조군과 비교할 경우 동일한 평균과 다른 분산 하에서 효과 크기가 달라지지 않도록 대조군에서 계산한 표준 편차만 사용하는 것이 낫다고 주장했다.

모집단 분산이 동일하다는 올바른 가정 하에서 θ에 대한 합동 추정치가 더 정확합니다.

헤지스 g

1981년 ^[27]래리 헤지스가 제안한 헤지스의 g는 표준화된 차이에^{[21]: 79} 기초한 다른 측정치와 같다.

${{displaystyle g=mar frac {\bar {x}_{1}-{\bar {x}}_{2}}{s^{*}}}}$

여기서 합동 표준 $편차{\displaystyle {}^{}}$ s $≤$ {\$style$ s$^{*}}$는 다음과 같이 계산된다:

${\displaystyle s^{*}=s_{1}^{2}+(n_{2}-1)s_{2}{2}{n_{1}+n_{2}-2}}.}$

그러나 모집단 효과 크기 θ의 추정치로서 편향되어 있다.그럼에도 불구하고, 이 편향은 인수에 의한 곱셈을 통해 대략적으로 보정될 수 있다.

${\displaystyle g^{*}=J(n_{1}+n_{2}-2),g, 약 \left(1-{\frac {3}{4(n_{1}+n_{2})-9}}\right,g},g}$

Hedges와 Olkin은 이 덜 치우친 $추정치{\displaystyle {}^{}}$ g ${\$ {\$displaystyle$ g$^{*}$을 ^[21]d라고 부르지만 Cohen의 d와 동일하지는 않습니다.보정 계수 J()의 정확한 형식은 감마 함수를^{[21]: 104} 포함합니다.

$({displaystyle J(a)=gamma(a/2)}{\gamrt {a/2,}}},\Gamma(a-1)/2)}}.}$

δ, 평균 제곱근 표준화 효과

다중 비교를 위한 유사한 효과 크기 추정기(예: 분산 분석)는 δ 평균 제곱근 표준화 ^[19]효과입니다.

${\displaystyle \Psi = rt {\frac {1}{k-1}\cdot \sum _{j=1}^{k}\leftfrac\frac {{j}-\mu}}{\frac }}{\fright}}}}}$

여기서 k는 비교 대상 그룹의 수입니다.

이는 기본적으로 d 또는 g와 유사한 루트 평균 제곱으로 조정된 전체 모델의 옴니버스 차이를 나타낸다.

또한 다요소 설계에 대한 일반화가 ^[19]제공되었습니다.

평균에 따른 효과 크기 분포

데이터가 가우스 분포의 Hedges' g, $n{\displaystyle \sqrt{{}_{}}}$ ${\displaystyle \sqrt{{1\mathrm{}}_{}}}$ ${\displaystyle \sqrt{{n\mathrm{}}_{}}}$2${\displaystyle \sqrt{}}$/ ( ${\displaystyle \sqrt{{n\mathrm{}}_{}}}$1 + ${\displaystyle \sqrt{{n\mathrm{}}_{}}}$2 )$$ { $displaystyle${$sqrt${$n _$ ${ n$ _ { n _ n _ {2$}$ } } 、 g$$} 、 ${\displaystyle \sqrt{{n1\mathrm{}}_{}}}$/${\displaystyle \sqrt{{n1\mathrm{}}_{}}}$ ${\displaystyle \sqrt{{}_{}}}$ $display$ ${\displaystyle style}$（ $n$$_$ { $n{\displaystyle \sqrt{{}_{}}}$ _ { 1 + n 2 ） ） 。}\$theta$} 및₁ (n₂ + n - 2) 자유도$.$마찬가지로 Scale Glass' δ는 n - 1 자유도로 분포되어₂ 있다.

분포로부터 효과 크기의 기대치와 분산을 계산할 수 있습니다.

경우에 따라서는 분산에 대해 큰 표본 근사치가 사용됩니다.Hedges의 편향되지 않은 추정치의^[21] 분산에 대한 한 가지 제안은 다음과 같다.

$(\displaystyle {\hat } ^{2}(g^{*}) = flac {n_{1} + n_{2}}{n_{1}n_{2}}+{\frac {(g^{*})^{2}}{2(n_{1}+n_{2}}}}.}$

기타 지표

Mahalanobis 거리(D)는 변수 ^[28]간의 관계를 고려한 Cohen의 d의 다변량 일반화입니다.

범주형 제품군: 범주형 변수 간의 연관성에 대한 효과 크기

$({displaystyle\varphi={frac{chi ^{2}}})$	$\displaystyle \varphi _{c}={frac {chi ^{2}}{N(k-1)}}}}$
파이())	크라메르의c V())

카이 제곱 검정에 일반적으로 사용되는 연관성 척도는 파이 계수와 크라메르의 V(때로는 크라메르의 파이라고도 하며 θ라고도_c 함)입니다.Phi는 점-이원 상관 계수와 코헨의 d와 관련이 있으며 두 변수 사이의 관계 범위를 추정한다(2 × 2).^[29]Cramér's V는 두 가지 이상의 수준을 가진 변수와 함께 사용할 수 있습니다.

파이(Phi)는 카이 제곱 통계량의 제곱근을 표본 크기로 나누어 계산할 수 있습니다.

마찬가지로 크라메르의 V는 카이 제곱 통계량의 제곱근을 표본 크기와 최소 치수의 길이로 나누어 계산합니다(k는 행 r 또는 열 c의 수보다 작음).

θ는_c 두 이산^[30] 변수의 상호 상관 관계이며 r 또는 c의 값에 대해 계산할 수 있다.그러나 카이 제곱 값이 셀 수에 따라 증가하는 경향이 있으므로 r과 c의 차이가 클수록 유의한 상관 관계가 있다는 강력한 증거가 없이 V가 1이 될 가능성이 높아집니다.

또한 Cramér의 V는 '적합성' 기판 모델(즉, c = 1인 모델)에도 적용할 수 있다.이 경우, 이것은 단일 결과(즉, k 결과 중)로 향하는 경향의 척도로 기능한다.이 경우 0 ~ 1 범위의 V를 유지하려면 k에 r을 사용해야 합니다.그렇지 않으면 c를 사용하면 방정식을 Phi의 방정식으로 줄일 수 있습니다.

코헨의 w

카이 제곱 검정에 사용되는 효과 크기의 또 다른 척도는 Cohen의 w입니다.이것은 다음과 같이 정의됩니다.

${{displaystyle w=sum_{i=1}^{m}{\frac {(p_{1i}-p_{0i}}}{p_{0i}}}}$

여기서_0i p는 H 아래의₀ i셀^th 값, p는_1i H 아래의₁ i셀^th 값, m은 셀 수입니다.

효과 크기	w
작은.	0.10
중간의	0.30
큰.	0.50

승산비

승산비(OR)도 유용한 효과 크기입니다.연구 질문이 두 이항 변수 간의 연관성에 초점을 맞출 때 적합합니다.예를 들어, 철자 능력에 대한 연구를 고려해 보십시오.관리 그룹에서는 불합격자 한 명당 두 명의 학생이 수업을 통과하므로 합격 확률은 2:1(또는 2/1 = 2)입니다.치료 그룹에서는 불합격자마다 6명의 학생이 합격하므로 합격 확률은 6:1(또는 6/1 = 6)입니다.효과 크기는 치료 그룹에서 통과 확률이 대조군 그룹보다 3배 높다는 점에 주목하여 계산할 수 있습니다(6 나누기 2는 3이므로).따라서 승산비는 3입니다.승산비 통계량은 Cohen의 d와 다른 척도에 있으므로 이 '3'은 Cohen의 d(3)와 비교할 수 없습니다.

상대 리스크

상대위험(R)은 위험비라고도 불리며, 단순히 일부 독립 변수에 대한 사건의 위험(확률)이다.효과 크기에 대한 이 측정값은 승산 대신 확률을 비교한다는 점에서 승산비와 다르지만 작은 확률에 대해서는 점근적으로 후자에 접근합니다.위의 예제를 사용하면 관리 그룹과 처리 그룹의 합격 확률은 각각 2/3(또는 0.67)와 6/7(또는 0.86)입니다.효과 크기는 위와 동일하게 계산할 수 있지만 대신 확률을 사용합니다.따라서 상대위험은 1.28이다.비교적 큰 통과 확률이 사용되었기 때문에, 상대적 위험과 승산비 사이에는 큰 차이가 있다.고장(더 작은 확률)을 사건(통과가 아닌)으로 사용한 경우 효과 크기에 대한 두 측정값 사이의 차이는 그리 크지 않을 것입니다.

두 측정 모두 유용하지만 통계적 용도는 다르다.의학 연구에서 승산비는 확률이 아닌 확률을 ^[31]추정하기 때문에 환자-대조군 연구에 일반적으로 사용됩니다.상대위험은 무작위 대조군 시험과 코호트 연구에서 일반적으로 사용되지만, 상대위험은 ^[32]개입 효과의 과대평가에 기여한다.

리스크의 차이

위험 차이(RD)는 절대 위험 감소라고도 불리며, 단순히 두 그룹 간 사건의 위험(확률) 차이이다.RD는 실험 개입이 사건 또는 결과의 확률을 변경하는 정도를 알려주므로 실험 연구에서 유용한 측도입니다.위의 예제를 사용하면 관리 그룹과 처리 그룹의 합격 확률은 각각 2/3(또는 0.67)와 6/7(또는 0.86)이므로 RD 효과 크기는 0.86 - 0.67 = 0.19(또는 19%)입니다.RD는 ^[32]개입의 효과를 평가하기 위한 우수한 척도입니다.

코헨의 h

두 독립적 비율을 비교할 때 검정력 분석에 사용되는 측도 중 하나는 Cohen의 h입니다.이것은 다음과 같이 정의됩니다.

${\displaystyle h=2(\arcsin {p_{1}}-\arcsin {\displaystyle {p_{2}})}$

여기서₁ p와₂ p는 비교 중인 두 표본의 비율이고 arcsin은 아크신 변환입니다.

공통 언어 효과 크기

효과 크기의 의미를 통계 밖의 사람들에게 더 쉽게 설명하기 위해, 이름에서 알 수 있듯이 공통 언어 효과 크기는 쉬운 영어로 전달되도록 설계되었다.두 그룹의 차이를 설명하기 위해 사용되며 1992년 ^[33]Kenneth McGraw와 S. P. Wong에 의해 제안되었다.그들은 다음 예시를 사용했다(남녀의 키에 대해서).공통 언어 효과 크기의 모집단 값을 설명할 때, "청년 남녀의 임의의 조합에서 남성이 여성보다 클 확률은 0.92이다. 더 쉽게 말하면, 청소년의 소개팅 100명 중 92명에서는 남성이 여성보다 클 것이다."^[33]

공통 언어 효과 크기에 대한 모집단 값은 모집단에서 무작위로 선택된 쌍에 대해 종종 다음과 같이 보고된다.Kerby(2014)는 한 그룹의 점수와 다른 그룹의 점수로 정의된 쌍이 공통 언어 효과 ^[34]크기의 핵심 개념이라고 지적한다.

또 다른 예로, 치료 그룹에 10명, 대조 그룹에 10명이 포함된 과학적 연구(관절염과 같은 일부 만성 질환에 대한 치료법일 수 있음)를 고려해 보십시오.치료 그룹의 모든 사람을 대조 그룹의 모든 사람과 비교하면 (10×10=) 100쌍이 있습니다.연구의 마지막에, 결과는 각 개인에 대해 점수로 평가되고(예를 들어 관절염 연구의 경우 이동성과 고통의 척도로 평가), 그리고 나서 모든 점수를 쌍 간에 비교한다.그 결과 가설을 뒷받침하는 쌍의 백분율이 공통 언어 효과 크기입니다.예제 연구에서 100개 비교 쌍 중 80개가 대조군 그룹보다 치료 그룹에 더 나은 결과를 보인다면, 보고서는 다음과 같이 읽을 수 있다. "치료 그룹의 환자가 대조군 그룹의 환자와 비교되었을 때, 치료된 환자가 100개 쌍 중 80개에서 더 나은 치료 결과를 보였다.come." 예를 들어, 이와 같은 연구에서 표본 값은 모집단 ^[35]값의 편향되지 않은 추정치입니다.

Vargha와 Delaney는 서수 수준 ^[36]데이터를 다루기 위해 공통 언어 효과 크기(Vargha-Delaney A)를 일반화했다.

순위-이계수 상관

공통 언어 효과 사이즈에 관련된 효과 사이즈는 랭크-바이서리 상관관계이다.이 측정치는 Mann-Whitney U ^[37]테스트의 효과 크기로서 Cureton에 의해 도입되었다.즉, 두 개의 그룹이 있으며 그룹의 점수가 등급으로 변환되었습니다.Kerby 단순 차분 공식은 공통 언어 효과 ^[34]크기에서 순위-이계 상관 관계를 계산한다.f를 가설에 유리한 쌍의 비율(공통 언어 효과 크기)로 하고, u를 바람직하지 않은 쌍의 비율이 되도록 하면, r = f - u라는 두 비율 사이의 단순한 차이가 된다.즉, 공통 언어 효과의 크기와 그 보완의 차이입니다.예를 들어, 공통 언어 효과 크기가 60%인 경우 랭크 쌍열 r은 60% - 40% 또는 r = 0.20입니다.Kerby 공식은 방향성이며, 양수 값은 결과가 가설을 뒷받침함을 나타냅니다.

Wendt는 순위-이계 상관관계에 대한 비방향식을 제공했고, 따라서 상관관계는 항상 ^[38]양수이다.Wendt 공식의 장점은 출판된 논문에서 쉽게 구할 수 있는 정보로 계산할 수 있다는 것이다.이 공식은 Mann-Whitney U 검정의 U 검정 값과 r = 1 – (2U)/(n₁₂ n) 두 그룹의 표본 크기만 사용합니다.여기서 U는 기존의 정의에 따라 데이터에서 계산할 수 있는 두 개의 U 값 중 작은 값으로 정의됩니다.그러면₁₂ 2U <nn이₁₂ U 통계정보의 최대값이 되므로 nn이 됩니다.

예를 들어 두 공식의 사용을 설명할 수 있습니다.치료 그룹에 10개, 대조 그룹에 10개 등 20명의 노인을 대상으로 한 건강 연구를 고려해 보십시오. 따라서 10쌍 또는 100쌍이 있습니다.건강 프로그램은 기억력을 향상시키기 위해 식이요법, 운동, 보충제를 사용하며 기억력은 표준화된 테스트를 통해 측정된다.Mann-Whitney U 테스트는 치료 그룹의 성인의 기억력이 100쌍 중 70쌍에서 더 좋았고 30쌍에서 더 나빴다는 것을 보여줍니다.Mann-Whitney U는 70과 30 중 더 작으므로 U = 30입니다.Kerby 단순 차이 공식에 의한 기억력과 치료 성능 사이의 상관 관계는 r = (70/100) - (30/100) = 0.40입니다.Wendt 공식에 의한 상관관계는 r = 1 - (2·30)/(10·10) = 0.40이다.

순서형 데이터의 효과 크기

Cliff's delta $또는{\displaystyle }$ d$\displaystyle$d는 원래 Norman Cliff가 순서형 ^[39]데이터에 사용하기 위해 개발한 것으로, 한 분포의 값이 두 번째 분포의 값보다 얼마나 큰지를 나타내는 척도입니다.결정적으로 두 분포의 형상이나 산포에 대한 가정을 필요로 하지 않습니다.

샘플 $추정치{\displaystyle }$ d$\displaystyle$d는$$ 다음과 같습니다.

${\displaystyle d=sum_{i,j}[x_{i}>x_{j}-[x_{i}<x_{j}}{mn}}$

여기서 두 분포의 $크기{\displaystyle }$n(\$displaystyle$ n$)$과 $m{\displaystyle {}_{}}$$(\displaystyle$ m$)$은 각각 $(\displaystyle x_i$}) 및 x$$$(\$이며$,{\displaystyle }$ [$](\displaystyle [\cdot$])은$$ Iverson 괄호이며, 즉 내용이 참일 경우 1, 거짓일 경우 0입니다.

$\displaystyle$d는 Mann-Whitney U 통계와 선형적으로 관련되지만, 기호에서 차이의 방향을 포착한다.$Mann-Whitney{\displaystyle }$U {\$displaystyle$ U$\}$의 경우 d$${\$displaystyle$ d$}$는 다음과 같습니다.

${\displaystyle d=mnfrac {2U}{mn}}-1}$

비중심성 모수에 의한 신뢰 구간

표준화된 효과 크기, 특히 코헨의 d$\$ $및$ $(\$ f$^{2$의 신뢰 구간은 비중심성 매개변수(ncp)의 신뢰 구간 계산에 의존합니다.ncp의 신뢰 구간을 구성하는 일반적인 접근법은 관찰된 통계를 꼬리 분위수 α/2 및 (1 - α/2)에 적합하도록 임계 ncp 값을 찾는 것이다.SAS 및 R 패키지 MBESS는 ncp의 임계값을 찾는 기능을 제공합니다.

t-단일 그룹 또는 두 관련 그룹의 평균 차이 검정

단일 그룹의 경우 M은 표본 평균을 나타내고, μ 모집단 평균, SD 표본 표준 편차, δ 모집단의 표준 편차, n은 표본 크기입니다.t 값은 평균과 기준선_baseline μ 사이의 차이에 대한 가설을 검정하는 데 사용됩니다.보통 μ는_baseline 0입니다.관련된 두 그룹의 경우 단일 그룹은 표본 쌍의 차이로 구성되며, SD와 θ는 원래 두 그룹 내가 아니라 표본과 모집단의 표준 차이 차이를 나타낸다.

${\displaystyle t:=flac {M-\mu _{\text{flac}}{\text{\text}}SE}} = flac {M-\mu _{\text{flac}} {\text{}SD}}/{\sqrt {n}}=sqrt {n}}\frac {M-\frac}{\frac}}\right}+{\frac {n}\frac {n}\frac {n}\frac {\text}}\fright}{\frac {\fr}}}}SD}}{\sigma}}}}}}$

${\displaystyle ncp=paramrt {n}\left frac {\text{param}}{\param}}\right}$

코헨의

${\displaystyle d:=flac {M-\mu _{\text{flac}}{\text{}}SD}}}}}:$

의 포인트 추정치입니다.

$(\displaystyle\frac\mu_{\text{{text}}{\displaystyle})}$

그렇게,

$(\displaystyle\tilde {d}}=snfrac {ncp}{\displayrt {n}}}).}$

t-독립된 두 그룹 간의 평균 차이 검정

n₁ 또는₂ n은 각각의 샘플 크기입니다.

${\displaystyle t:=flac {M_{1}-M_{2}}{\text{\text}SD}}_{\text{within}/{\sqrt {\frac {2*n_{1}n_{2}}{n_{1}+n_{2}}}}}}},}$

여기서

$디스플레이 스타일SD}_{\text{within}}:={frac{\text{\text}가 아닙니다.SS}_{\text{within}}{\text{df}_{\text{within}}}=sqrt {(n_{1}-1){\text{\text}SD}_{1}^{2}+(n_{2}-1){\text{SD}_{2}^{2}}{n_{1}+n_{2}-2}}}.}$

${\displaystyle ncp=syslogrt {frac {n_{1}n_{2}}{n_{1}+n_{2}}}}{\frac {{1}-\mu _{2}}{\frac }}$

코헨의

$displaystyle$$$$SD_{\text{within}}}}$는${\displaystyle \frac{{}_{}{}_{}}{}}$ ~ ${\displaystyle \frac{{\mu 2\mathrm{}}_{}}{}}$ ${\displaystyle †}$의 포인트 추정치입니다$.{$ $displaystyle${$frac _$ ${$1$}$ - \ $mu$_ {2$}$ } { \ $sigma }$ 。$}$

그렇게,

${\displaystyle {d} = snfrac {ncp} {\snfrac {n_{1}n_{2} {n_{1} + n_{2}}}}}}.}$

여러 독립 그룹 간의 평균 차이에 대한 일원 분산 분석 검정

일원 분산 분석 검정은 비중심 F 분포를 적용합니다.특정 모집단 표준 $편차{\displaystyle }$ ${\$ {\$displaystyle \sigma$인 경우 동일한 테스트 문제가 비중심 카이 제곱 분포를 적용합니다.

${\displaystyle F:=frac {{\frac {\text}SS}_{\text{between}}{\sigma ^{2}}/{\text{df}_{\text{between}}}{\frac{\text{}SS}_{\text{within}}{\sigma ^{2}}/{\text{df}}_{\text{within}}}}}$

i번째 그룹_i,j X 내의 각 j번째 샘플에 대해, 다음을 나타낸다.

${\displaystyle M_{i}(X_{i,j):=440frac {{w=1}^{n_{i}X_{i,w}}{n_{i}};\mu_{i}(X_{i,j}):=\mu _{i}.}$

하는 동안에,

$\displaystyle \ signed \ text \SS}_{\text{between}}/\sigma^{2}&=sigma frac {{\text{}SS}}\left(M_{i}(X_{i,j});i=1,2,\dots,K,\;j=1,2,\dots,n_{i}\오른쪽)}{\syslog ^{2}}\&= 텍스트{\&}SS}}\left({\frac {M_{i}(X_{i,j}-\mu _{i}})}{\frac {{i}}{\frac}}};i=1,2,\frac,K,\dots,n_i}\오른쪽)\\&\sim \chi ^{2}\left({\text{df}})=K-1,\;ncp=SS\left({\frac {i}(X_{i,j})}{\sigma}};i=1,2,\dots,n_{i}\right)\end{aligned}}$

따라서 F의 ncp(s)와 § $(\$^{$2})$는 모두 다음과 같습니다.

$디스플레이 스타일SS}}\left(\mu _{i}(X_{i,j})/\sigma;i=1,2,\sigma,K,\;j=1,2,\dots,n_{i}\right).}$

n : ${\displaystyle =}$ ${\displaystyle {n\mathrm{}}_{}}$ 1 ${\displaystyle {}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle \cdots }$ ${\displaystyle =}$ ${\displaystyle {}_{}}$ ${\displaystyle K_{}}${ $displaystyle$ n : =$n$_ { n _ { } =\$cdots$=$n$_ { $K$}인$$ $경우{\displaystyle }$, 같은 크기의 K개 독립군에 대하여 총 시료 크기는 N : = n · K이다.

${\displaystyle {Cohens}}{\tilde {f}}^2}: = flac {{\text}SS}}(\mu _{1},\mu _{2},\mu _{K}){K\cdot \cdot ^{2}}=mu frac {\text{}SS}}\left(\mu _{i}(X_{i,j})/\sigma;i=1,2,\sigma,K,\;j=1,2,\dots,n_{i}\right)}{n\cdot K}=snfrac {ncp}{n\cdot K}=snfrac {ncp}{N}}.}$

독립 그룹 쌍에 대한 t-검정은 일원 분산 분석의 특수한 경우입니다.non centrality $파라미터{\displaystyle }$ ${\displaystyle n}$ ${\displaystyle {cp}_{}}$ F$(\$에 주의해 주십시오.F의 F$}$는 대응하는 t의 비중심성 $파라미터{\displaystyle }$ ${\displaystyle n}$ ${\displaystyle {cp}_{}}$ t$${$displaystyle ncp_{t}$와 동등하지 않다.$실제로$는 n ${\displaystyle {}_{}}$ ${\displaystyle p_{}}$ F ${\displaystyle {}_{}n}$ c ${\displaystyle p_{}^{}}$ ${\displaystyle {\mathrm{}}_{}^{}}$2 (\$displaystyle ncp_{)$$F}=ncp_{t}^$2$\}\}$ $및{\displaystyle \stackrel{}{}}$ f${\displaystyle \stackrel{}{}}$~ $=$ ~${\displaystyle }{\displaystyle \frac{2}{\mathrm{}}}$({$displaystyle {f$}=\$left({frac$ {$tilde$ {d$}}{2}}\right$

「 」를 참조해 주세요.

• 추정통계
• 통계적 유의성
• Z-요인, 효과 크기의 대체 측도

레퍼런스

추가 정보

• Aaron, B., Kromrey, J. D. 및 Feron, J. M. (1998년, 11월).r 기반 및 d 기반 효과 크기 지수 동일화: 일반적으로 권장되는 공식의 문제.플로리다 주 올랜도, 플로리다 교육 연구 협회 연례 회의에서 발표된 논문(ERIC 문서 재생 서비스 번호 ED433353)
• Bonett, D. G. (2008). "Confidence intervals for standardized linear contrasts of means". Psychological Methods. 13 (2): 99–109. doi:10.1037/1082-989x.13.2.99. PMID 18557680.
• Bonett, D. G. (2009). "Estimating standardized linear contrasts of means with desired precision". Psychological Methods. 14 (1): 1–5. doi:10.1037/a0014270. PMID 19271844.
• Brooks, M.E.; Dalal, D.K.; Nolan, K.P. (2013). "Are common language effect sizes easier to understand than traditional effect sizes?". Journal of Applied Psychology. 99 (2): 332–340. doi:10.1037/a0034745. PMID 24188393.
• Cumming, G.; Finch, S. (2001). "A primer on the understanding, use, and calculation of confidence intervals that are based on central and noncentral distributions". Educational and Psychological Measurement. 61 (4): 530–572. doi:10.1177/0013164401614002. S2CID 120672914.
• Kelley, K (2007). "Confidence intervals for standardized effect sizes: Theory, application, and implementation". Journal of Statistical Software. 20 (8): 1–24. doi:10.18637/jss.v020.i08.
• Lipsey, M. W., & Wilson, D. B. (2001)실용적인 메타 분석.사우전드 오크, 캘리포니아

외부 링크

상세설명

• 효과 크기(ES)
• 효과 크기FAQ.com
• EstimationStats.com 효과 크기 플롯 생성용 웹 앱입니다.
• 측정 효과 크기
• ViSta를 사용한 효과 크기 측정값 계산 및 해석
• 통계 컴퓨팅을 위한 R 프로젝트용 emphize 패키지