비선형 회귀 분석

시리즈의 일부
회귀 분석
모델
선형 회귀 단순 회귀 다항식 회귀 분석 일반 선형 모형
일반화 선형 모형 개별 선택 이항 회귀 분석 이항 회귀 로지스틱 회귀 분석 다항 로지스틱 회귀 분석 혼합 로짓 프로빗 다항 프로빗 주문된 로짓 순서 프로빗 포아송
다단계 모형 고정 효과 랜덤 효과 선형 혼합 효과 모형 비선형 혼합 효과 모형
비선형 회귀 분석 비모수 반파라메트릭 견고. 양분위수 아이소토닉 주요 컴포넌트 최소 각도 현지의 세그먼트화
변수 오류
견적
최소 제곱 선형 비선형
보통의 가중치 일반화
부분적 총 음이 아닌 능선 회귀 정규화
최소 절대 편차 반복 재중량화 베이지안 베이지안 다변량 최소 제곱 스펙트럼 분석
배경
회귀 검증 평균 및 예측 반응 오차 및 잔차 적합도 학생화 잔차 가우스-마르코프 정리
수학 포털
v t

통계학에서 비선형 회귀는 모형 모수의 비선형 조합인 함수에 의해 관측 데이터가 모형화되는 회귀 분석의 한 형태입니다.데이터는 연속적인 근사 방법으로 적합됩니다.

일반

비선형 회귀 분석에서 형태의 통계 모형은

$(\displaystyle \mathbf {y} \sim f(\mathbf {x} , {\boldsymbol {x}} )$

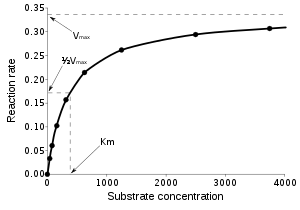
는 독립 변수의 $벡터{\displaystyle \mathbf{}}$x ${\displaystyle \mathbf$ {$x$ 와 관련 관찰된 종속 $변수{\displaystyle \mathbf{}}$y {\$displaystyle \mathbf$ {y$\}\}$$$에 관련됩니다. $f{\displaystyle }$$${\$displaystyle$$f}$ 함수는$$ $파라미터{\displaystyle }$$β$의 벡터 성분에서 비선형이지만 그 이외의 경우에는 임의입니다.예를 들어 효소 동태에 대한 Michaelis-Menten 모델에는 다음과 같은 방법으로$$^[a]f\$displaystyle$와 관련된 두 개의 매개 변수와 하나의 독립 변수가 있다.

${\displaystyle f(x,\boldsymbol {\x})=black {\display_{1}x}{\display_{2}+x}}$

이 함수는 $2개$의$$β\$displaystyle\beta }$의 선형 조합으로 표현할 수 없기 때문에 비선형적입니다.

독립 변수에 체계적 오류가 있을 수 있지만 그 처리는 회귀 분석의 범위를 벗어납니다.독립 변수가 오류가 없는 경우 이 범위 밖에도 있는 변수 오류 모델입니다.

비선형 함수의 다른 예로는 지수 함수, 로그 함수, 삼각 함수, 멱함수, 가우스 함수, 로렌츠 분포 등이 있습니다.지수함수나 로그함수와 같은 일부 함수는 선형으로 변환할 수 있습니다.변환된 경우 표준 선형 회귀 분석을 수행할 수 있지만 주의해야 합니다.상세한 것에 대하여는, 다음의 「Linearization」 「Transformation」을 참조해 주세요.

일반적으로 선형 회귀 분석에서와 같이 최적 모수에 대한 닫힌 형식 표현식은 없습니다.일반적으로 수치 최적화 알고리즘은 최적의 파라미터를 결정하기 위해 적용됩니다.선형 회귀 분석과 대조적으로 최적화할 함수의 국소 최소값이 많을 수 있으며 전역 최소값도 편향된 추정치를 생성할 수 있다.실제로 모수의 추정치는 최적화 알고리즘과 함께 제곱합에 대한 전역 최소값을 찾기 위해 사용됩니다.

비선형 데이터 모형화에 대한 자세한 내용은 최소 제곱 및 비선형 최소 제곱을 참조하십시오.

회귀 통계량

이 절차의 기초가 되는 가정은 모델이 선형 함수, 즉 1차 테일러 급수에 의해 근사될 수 있다는 것입니다.

$\displaystyle f(x_{i},{\boldsymbol\beta }}\about f(x_{i},0)+\sum _{j}J_{ij}\beta _{j}$

$여기$서 ${\displaystyle {\mathrm{Ji}}_{}}$ j $=$ ${\displaystyle \partial \frac{\mathrm{}f}{}}$ ( ${\displaystyle \frac{{}_{}{i}_{}}{}}$ ,${\displaystyle \frac{\beta \mathit{}}{}}$ ) β${\displaystyle \frac{\mathrm{}{\beta }_{}}{}}$j { $displaystyle J_{ij$}= $fr$ frac {\$boldsymbol$ {\$bold$symbol$}{\symbol$ _${i$ 여기서 최소 제곱 추정치는 다음과 같이 주어진다.

${\displaystyle\hat\boldsymbol\beta}\about\mathbf {(J^{T}J)^{-1}J^{T}y},},}$

일반화 최소 제곱을 단위 행렬에 비례하는 공분산 행렬과 비교합니다.비선형 회귀 통계량은 선형 회귀 통계량에서와 같이 계산 및 사용되지만 공식에서 X 대신 J를 사용합니다.선형 근사는 통계량에 편향을 가져옵니다.따라서 비선형 모형에서 파생된 통계량을 해석할 때는 평소보다 더 주의해야 합니다.

일반 및 가중 최소 제곱

최적 적합 곡선은 잔차 제곱의 합을 최소화하는 곡선으로 가정하는 경우가 많습니다.이것은 일반 최소 제곱법(OLS) 접근법입니다.그러나 종속 변수의 분산이 일정하지 않은 경우에는 가중 제곱 잔차의 합을 최소화할 수 있습니다. 자세한 내용은 가중 최소 제곱을 참조하십시오.각 가중치는 이상적으로는 관측치 분산의 역수와 동일해야 하지만 가중치는 반복할 때마다 반복 최소 제곱 알고리즘에서 재계산될 수 있다.

선형화

변혁

일부 비선형 회귀 문제는 모형 공식의 적절한 변환을 통해 선형 영역으로 이동할 수 있습니다.

예를 들어, 비선형 회귀 분석 문제를 고려합니다.

$(\displaystyle y=ae^{bx}U,\!)$

변수 a와 b와 곱셈 오차항 U를 사용한다. 만약 우리가 양쪽의 대수를 취한다면, 이것은

$\displaystyle \ln {(y)}=\ln {(a)}+bx+u,\!}$

여기서 u = ln(U), x의 ln(y)의 선형 회귀에 의한 알 수 없는 모수의 추정을 제안하며, 반복 최적화가 필요하지 않은 계산이다.그러나 비선형 변환을 사용하려면 주의가 필요합니다.모형의 오차 구조와 추리 결과의 해석과 마찬가지로 데이터 값의 영향도 변화합니다.이러한 효과는 바람직하지 않을 수 있습니다.한편, 가장 큰 오차 발생원에 따라 비선형 변환은 오차를 가우스 방식으로 분산시킬 수 있으므로 비선형 변환을 수행할 선택은 모델링 고려사항에 의해 통지되어야 합니다.

Michaelis-Menten 역학의 경우 선형 Lineweaver-Burk 그림

$({displaystyle {1}{v}}=black {1}{V_{\max}}+{\flac {K_{m}}{V_{\max}[S]}})$

1/v 대 1/[S]의 값이 많이 사용되고 있습니다.그러나 데이터 오류에 매우 민감하고 독립 변수의 특정 범위인 [S]에 데이터를 적합시키는 데 강한 편중이 있으므로 사용을 강력히 권장하지 않는다.

지수 패밀리에 속하는 오차 분포의 경우 링크 함수를 사용하여 일반화 선형 모델 프레임워크에서 매개변수를 변환할 수 있습니다.

세그멘테이션

독립 변수 또는 설명 변수(예: X)는 클래스 또는 세그먼트로 분할할 수 있으며 세그먼트당 선형 회귀 분석을 수행할 수 있습니다.신뢰 분석을 사용한 세그먼트 회귀 분석에서는 종속 변수 또는 반응 변수(예: Y)가 다양한 ^[1]세그먼트에서 다르게 동작하는 결과를 얻을 수 있습니다.

이 수치는 토양 염도(X)가 처음에는 임계치 또는 한계치(절단점)까지 겨자 수확량(^[2]Y)에 영향을 미치지 않는다는 것을 보여준다.

「 」를 참조해 주세요.

• 비선형 최소 제곱
• 곡선 피팅
• 일반화 선형 모형
• 국소 회귀
• 응답 모델링 방법론
• 유전자 프로그래밍
• 다중 표현식 프로그래밍

레퍼런스

메모들

추가 정보

• Bethea, R. M.; Duran, B. S.; Boullion, T. L. (1985). Statistical Methods for Engineers and Scientists. New York: Marcel Dekker. ISBN 0-8247-7227-X.
• Meade, N.; Islam, T. (1995). "Prediction Intervals for Growth Curve Forecasts". Journal of Forecasting. 14 (5): 413–430. doi:10.1002/for.3980140502.
• Schittkowski, K. (2002). Data Fitting in Dynamical Systems. Boston: Kluwer. ISBN 1402010796.
• Seber, G. A. F.; Wild, C. J. (1989). Nonlinear Regression. New York: John Wiley and Sons. ISBN 0471617601.