백분위수
Percentile통계학에서 k번째 백분위수는 백분위수 점수 또는 백분위수 점수라고도 하며, 빈도 분포에서 점수의 특정 백분위수 k가 ("전속적" 정의") 아래에 있는 점수 또는 특정 백분위수가 ("전속적" 정의) 아래에 있는 점수입니다.백분위수는 입력 점수와 동일한 측정 단위로 표시되며 백분위수는 백분위가 아닙니다. 예를 들어 점수가 인체 중량을 나타내는 경우 해당 백분위수는 킬로그램 또는 파운드로 표시됩니다.무한 표본 크기의 한계에서 백분위수는 누적 분포 함수의 역수인 백분위수 함수에 근사합니다.
백분위수는 분위수의 한 종류로, 100개의 그룹으로 세분화하여 얻은 것입니다.25번째 백분위수는 1분위(Q1), 50번째 백분위수는 중위수 또는 2분위(Q2), 75번째 백분위수는 3분위(Q3)라고도 합니다.예를 들어, 50번째 백분위수(중앙값)는 분포에서 50%의 점수가 발견되는 아래(정의에 따라 또는 아래)의 점수입니다.
관련 수량은 점수의 백분위 순위로, 백분위로 표시되며, 이는 분포에서 점수가 그보다 작은 부분을 나타내는 것으로, 배타적인 정의입니다.백분위 점수와 백분위 순위는 표준 참조 시험의 시험 점수를 보고하는 데 종종 사용되지만, 방금 언급한 바와 같이 동일하지 않습니다.백분위수 순위의 경우 점수가 부여되고 백분율이 계산됩니다.백분위수 순위는 배타적입니다. 지정된 점수의 백분위수 순위가 90%인 경우 점수의 90%가 더 낮습니다.반면 백분위수의 경우 백분위수가 주어지고 해당 점수가 결정되며, 이 점수는 배타적이거나 포괄적일 수 있습니다.지정된 백분율(예: 90번째)에 대한 점수는 분포의 다른 점수(예: 배타적 정의) 또는 그 이하(포함 정의)에 해당하는 점수를 나타냅니다.
정의들
백분위수에 대한 표준 정의는 없지만 [1][2][3]관측치의 수가 매우 많고 확률 분포가 연속적인 경우에는 모든 정의에서 유사한 결과를 얻을 수 있습니다.[4]한계치에서, 표본 크기가 무한대에 가까워질수록th 100p 백분위수(0<p<1)는 p가 CDF에 근접함에 따라 p에서 평가된 누적 분포 함수(CDF)의 역에 근접합니다.이는 글리벤코-칸텔리 정리의 결과로 볼 수 있습니다.백분위수를 계산하는 몇 가지 방법이 아래에 나와 있습니다.
정규 분포 및 백분위수

계산 방법 섹션(아래)에 나와 있는 방법은 소표본 통계량에 사용하기 위한 근사치입니다.일반적으로 정규 분포를 따르는 매우 큰 모집단의 경우 백분위수가 정규 곡선 그림을 참조하여 표시되는 경우가 많습니다.정규 분포는 표준 편차 또는 시그마(Sigma) 단위로 축척된 축을 따라 표시됩니다. (σ 단위.수학적으로 정규 분포는 왼쪽의 음의 무한대와 오른쪽의 양의 무한대로 확장됩니다.그러나 모집단에서 매우 적은 수의 개체만이 -3 σ ~ +3 σ 범위 밖에 있습니다.예를 들어, 사람 키의 경우 +3 σ 키 수준 이상인 사람은 거의 없습니다.
백분위수는 정규 곡선 아래의 영역을 나타내며 왼쪽에서 오른쪽으로 증가합니다.각 표준 편차는 고정 백분위수를 나타냅니다.따라서 소수점 두 자리로 반올림하면 -3 σ는 0.13번째 백분위수, -2 σ은 2.28번째 백분위수, -1 σ은 15.87번째 백분위수, 0 σ은 50번째 백분위수(분포의 평균과 중앙값), +1 σ은 84.13번째 백분위수, +2 σ은 97.72번째 백분위수, +3 σ은 99.87번째 백분위수입니다.이것은 68–95–99.7 규칙 또는 3-시그마 규칙과 관련이 있습니다.이론적으로 0번째 백분위수는 음의 무한대에서, 100번째 백분위수는 양의 무한대에서 떨어지지만, 테스트 결과와 같은 많은 실제 적용에서는 자연 하한 및/또는 상한이 적용됩니다.
적용들
ISP가 인터넷 대역폭을 "버스터블"로 청구할 때, 95번째 또는 98번째 백분위수는 일반적으로 매달 대역폭의 최고 5% 또는 2%를 끊은 다음에 가장 가까운 비율로 청구합니다.이와 같이, 빈번하지 않은 피크는 무시되고, 고객은 보다 공정한 방식으로 요금을 청구하게 됩니다.이 통계가 데이터 처리량을 측정하는 데 매우 유용한 이유는 대역폭의 비용을 매우 정확하게 보여주기 때문입니다.95번째 백분위수는 95%의 경우 사용량이 이 금액 이하라고 합니다. 따라서 나머지 5%의 경우 사용량이 이 금액 이상이라고 합니다.
의사들은 성장 차트에서 볼 수 있는 전국 평균 및 백분위수와 비교하여 성장을 평가하기 위해 유아 및 어린이의 몸무게와 키를 자주 사용합니다.
도로의 통행속도 85분위수는 제한속도를 설정하고 제한속도가 너무 높은지 낮은지를 평가할 때 종종 지침으로 사용됩니다.[5][6]
금융에서 위험가치(Value at risk)는 포트폴리오의 가치가 일정 기간 내에 하락하지 않을 것으로 예상되는 수량을 평가하고 신뢰가치를 부여하는 표준적인 측정치입니다.
계산방법
백분위 점수에는 많은 공식이나 알고리즘이[7] 있습니다.Hyndman과 Fan은 9개의 소프트웨어와 대부분의 통계 및 스프레드시트 소프트웨어가 그들이 설명하는 방법 중 하나를 사용한다는 것을 확인했습니다.[8]알고리즘은 점수 집합에 존재하는 점수의 값을 반환하거나(가장 가까운 순위의 방법) 기존 점수 사이를 보간하며 배타적이거나 포괄적입니다.
| PC: 백분위수 지정 | 0.10 | 0.25 | 0.50 | 0.75 | 0.90 |
|---|---|---|---|---|---|
| N: 점수수 | 10 | 10 | 10 | 10 | 10 |
| OR : 서수 순위 = PC × N | 1 | 2.5 | 5 | 7.5 | 9 |
| 순위: >OR / ≥OR | 2/1 | 3/3 | 6/5 | 8/8 | 10/9 |
| 순위점수(ex/inc) | 2/1 | 3/3 | 4/3 | 5/5 | 7/5 |
그림은 10-score 분포를 보여주고, 이러한 다양한 알고리즘의 결과로 나타나는 백분위 점수를 보여주며, 이후에 주어진 예제에 대한 소개 역할을 합니다.가장 간단한 것은 분포에서 점수를 반환하는 가장 가까운 순위 방법이지만 보간 방법과 비교하면 결과가 다소 조잡할 수 있습니다.Nearest-Rank Methods 표는 배타적 방법과 포괄적 방법에 대한 계산 단계를 보여줍니다.
| PC: 백분위수 지정 | 0.10 | 0.25 | 0.50 | 0.75 | 0.90 |
|---|---|---|---|---|---|
| N: 점수수 | 10 | 10 | 10 | 10 | 10 |
| OR : PCx(N+1) / PCx(N-1)+1 | 1.1/1.9 | 2.75/3.25 | 5.5/5.5 | 8.25/7.75 | 9.9/9.1 |
| LoRank: 또는 잘림 | 1/1 | 2/3 | 5/5 | 8/7 | 9/9 |
| Hirank: 또는 반올림됨 | 2/2 | 3/4 | 6/6 | 9/8 | 10/10 |
| LoScore: LoRank에서의 점수 | 1/1 | 2/3 | 3/3 | 5/4 | 5/5 |
| HiScore: HiRank 점수 | 2/2 | 3/3 | 4/4 | 5/5 | 7/7 |
| 차이점:HiScore − LoScore | 1/1 | 1/0 | 1/1 | 0/1 | 2/2 |
| 모드: OR의 일부분 | 0.1/0.9 | 0.75/0.25 | 0.5/0.5 | 0.25/0.75 | 0.9/0.1 |
| 보간점수(ex/inc) = LoScore + Mod × Difference | 1.1/1.9 | 2.75/3 | 3.5/3.5 | 5/4.75 | 6.8/5.2 |
보간 방법은 이름에서 알 수 있듯이 분포의 점수 사이에 있는 점수를 반환할 수 있습니다.통계 프로그램에서 사용하는 알고리즘은 일반적으로 Microsoft Excel의 percentile.exc와 percentile.inc 함수와 같은 보간 방법을 사용합니다.Interpolated Methods 표에는 계산 단계가 나와 있습니다.
가장 가까운 순위의 방법
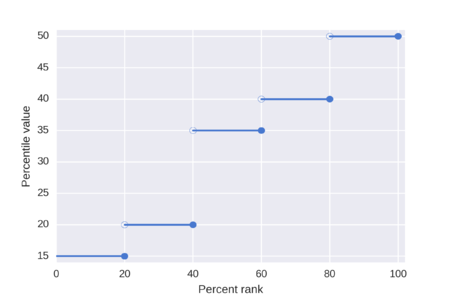
백분위수의 한 정의는 종종 텍스트로 주어지는데,N개의 순서 값 목록(최소에서 최대로 정렬됨)의 P번째 백분위수< ) < 가 목록에서 가장 작은 값이며 데이터의 P% 이상이 값보다 엄격하게 작거나 같은 값입니다.이것은 먼저 순서 순위를 계산한 다음 해당 순위에 해당하는 순서 목록에서 값을 가져옴으로써 얻어집니다.순서 순위 n은 이 공식을 사용하여 계산됩니다.
- 서로 다른 값이 100개 미만인 목록에서 가장 가까운 순위 방법을 사용하면 같은 값이 백분위수 이상에 사용될 수 있습니다.
- 가장 가까운 순위 방법을 사용하여 계산된 백분위수는 항상 원래 순서 목록의 멤버가 됩니다.
- 100번째 백분위수는 순서 목록에서 가장 큰 값으로 정의됩니다.
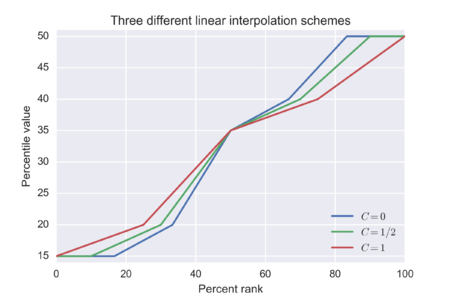
가장 가까운 순위 사이의 선형 보간 방법
많은 응용 프로그램에서 사용되는 반올림의 대안은 인접한 순위 간에 선형 보간을 사용하는 것입니다.
다음 변형들은 모두 다음과 같은 공통점을 가지고 있습니다.주문통계가 주어지면
점( 을 통과하는 선형 보간 함수를 찾습니다 이것은 단순히 다음과 같이 수행됩니다.
여기서 ⌊ ⌋ 은(는) 양의 x의 적분 부분을 나타내는 바닥 함수를 사용하는 , x 1 {\ {1은(는) 부분 부분 부분을 나타내는 mod 함수를 사용합니다(단, x = N x=에서는 ⌊ ⌋+ ).은(는) 정의되지 않았습니다. 1}} 을(를) 곱했기 때문에 그럴 필요는 없습니다.)우리가 볼 수 있듯이, x는 첨자의 연속 버전이며, 인접한 노드 사이에 v를 선형 보간합니다.
변형 접근 방식은 두 가지 방법으로 다릅니다.첫 번째는 순위 x, 백분율 순위 = P = 및 표본 크기 N의 함수인 상수 사이의 선형 관계입니다.
중위수에 해당하는범위 의 중간점이 = p = 에서 발생해야 하는 추가 요구 사항이 있습니다
그리고 우리의 수정된 기능은 이제 다음과 같이 자유도가 하나밖에 없습니다.
변형이 다른 두 번째 방법은 범위의 p: 범위에서 함수를 정의하는 것입니다 [ 범위의 결과를 생성하거나 강제로 생성해야 합니다더 넓은 지역에 일대일 대응의 부재를 의미할 수도 있습니다한 저자는 = ( +ξ C = {\ 중 하나를 선택할 것을 제안했습니다. 여기서 ξ은 표본 분포의 극단값 한계인 일반화된 극단값 분포의 모양입니다.
첫 번째 변형, C = 1/2
(출처: Matlab "practile" 함수, [9][10])
어디에
게다가, let.
역 관계는 더 좁은 영역으로 제한됩니다.
두 번째 변형, C = 1
(출처:NumPy[11] 및 Microsoft Excel을[3] 포함한 일부 소프트웨어 패키지(PENCERTILE을 통해 2013 버전까지 포함)INC 함수).NIST에서[8] 대안으로 언급)
↔ right arrow 관계는 ∈[ p에 대해 일대일 관계이며 이 속성을 가진 세 가지 변형 중 유일한 것입니다. 따라서 Excel 함수에 "INC" 접미사가 포함됩니다.
세 번째 변형, C = 0
(NIST가 권장하는 1차 변형.[8]2010년부터 마이크로소프트 엑셀에서 PENCERTIL을 통해 채택.EXC 기능.그러나 "EXC" 접미사에서 알 수 있듯이 Excel 버전에서는 p 범위의 두 , 즉 p ∈(1) {\ p (1)}이(가) 제외된 반면두 번째 변형인 "INC" 버전에서는 제외되지 않습니다. 실제로 + 1 보다 작은 숫자도 제외되므로 오류가 발생합니다.)
역은 더 좁은 영역으로 제한됩니다.
가중 백분위수 방법
백분위수 함수 외에 가중 백분위수도 있는데, 여기서는 총 무게에서 총 무게의 백분율이 계산됩니다.가중 백분위수에 대한 표준 함수가 없습니다.하나의 방법은 상기 접근법을 자연스러운 방식으로 확장합니다.
양의 가중치 가 각각 N개 정렬된 샘플 값과 연관되어 있다고 가정합니다.
무게의 총합그러면 위의 공식들은 다음을 취함으로써 일반화됩니다.
- 1 }={\ {일 때 C
아니면
- - + (- }={\ - - 2 n}}}, C {\ C
그리고.
참고 항목
참고문헌
- ^ a b Hyndman, Rob J.; Fan, Yanan (November 1996). "Sample Quantiles in Statistical Packages". American Statistician. American Statistical Association. 50 (4): 361–365. doi:10.2307/2684934. JSTOR 2684934.
- ^ Lane, David. "Percentiles". Retrieved 2007-09-15.
- ^ a b Pottel, Hans. "Statistical flaws in Excel" (PDF). Archived from the original (PDF) on 2013-06-04. Retrieved 2013-03-25.
- ^ Schoonjans F, De Bacquer D, Schmid P (2011). "Estimation of population percentiles". Epidemiology. 22 (5): 750–751. doi:10.1097/EDE.0b013e318225c1de. PMC 3171208. PMID 21811118.
- ^ Johnson, Robert; Kuby, Patricia (2007), "Applied Example 2.15, The 85th Percentile Speed Limit: Going With 85% of the Flow", Elementary Statistics (10th ed.), Cengage Learning, p. 102, ISBN 9781111802493.
- ^ "Rational Speed Limits and the 85th Percentile Speed" (PDF). lsp.org. Louisiana State Police. Archived from the original (PDF) on 23 September 2018. Retrieved 28 October 2018.
- ^ Wessa, P (2021). "Percentiles in Free Statistics Software". Office for Research Development and Education. Retrieved 13 November 2021.
- ^ a b c "Engineering Statistics Handbook: Percentile". NIST. Retrieved 2009-02-18.
- ^ "Matlab Statistics Toolbox – Percentiles". Retrieved 2006-09-15."Matlab Statistics Toolbox – Percentiles". Retrieved 2006-09-15.이것은 여기서 논의된 방법 5와 동등합니다.
- ^ Langford, E. (2006). "Quartiles in Elementary Statistics". Journal of Statistics Education. 14 (3). doi:10.1080/10691898.2006.11910589.
- ^ "NumPy 1.12 documentation". SciPy. Retrieved 2017-03-19.
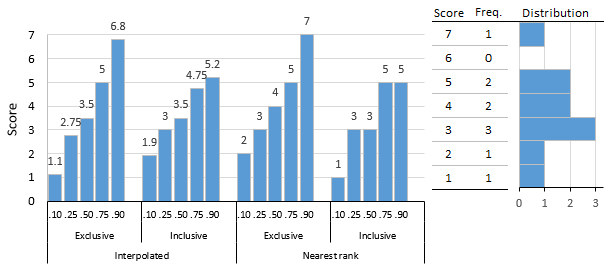




![{\displaystyle v(x)=v_{\lfloor x\rfloor }+(x{\bmod {1}})(v_{\lfloor x\rfloor +1}-v_{\lfloor x\rfloor }),\forall x\in [1,N]:v(i)=v_{i}{\text{, for }}i=1,2,\ldots ,N,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eeae87405f0184fabff114665b843cbb94a3abbc)



![[0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d) p:
p: 
![[1,N]](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6fc7b14276a914ff6cbdf59b806eb601020f473)
![{\displaystyle x=f(p)={\begin{cases}Np+{\frac {1}{2}},\forall p\in \left[p_{1},p_{N}\right],\\1,\forall p\in \left[0,p_{1}\right],\\N,\forall p\in \left[p_{N},1\right].\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7800366b8eeac526ee3fc22b45ed5dfd1550e62)
![p_{i}={\frac {1}{N}}\left(i-{\frac {1}{2}}\right),i\in [1,N]\cap \mathbb {N}](https://wikimedia.org/api/rest_v1/media/math/render/svg/69e7a4bfdbaf07f8b5e36ccd021ff966f5e540d3)



![x=f(p,N)=p(N-1)+1{\text{, }}p\in [0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/e25ef7db919bca75354f8af45d7208a1c5a626b2)
![\therefore p={\frac {x-1}{N-1}}{\text{, }}x\in [1,N].](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a4c15310db22c92a626068484739e320bace185)
![{\displaystyle x=f(p,N)={\begin{cases}1{\text{, }}p\in \left[0,{\frac {1}{N+1}}\right]\\p(N+1){\text{, }}p\in \left({\frac {1}{N+1}},{\frac {N}{N+1}}\right)\\N{\text{, }}p\in \left[{\frac {N}{N+1}},1\right]\end{cases}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e7bef62b06df2ee9322c8ac5b1d10b43c07176f6)