균질성 및 이질성

균질성을 나타내는 랜덤 데이터를 사용하여 그림: x의 각 값에서 점의 y-값은 분산이 거의 동일합니다.

이질적 탄성을 나타내는 랜덤 데이터를 사용한 그림:점의 y 값 분산은 x 값이 증가할수록 증가합니다.

통계학에서 랜덤 변수의 시퀀스(또는 벡터)는 모든 랜덤 변수가 동일한 유한 분산을 갖는 경우 호모세카스틱(/hohomomoskskˈdéstkk/)이다.이를 분산의 균질성이라고도 합니다.이 상호보완적 개념은 이질적 특성이라고 불린다.철자 동형성 및 이형성 또한 ^[1]^[2]^[3]자주 사용된다.

변수가 실제로 이질적인 경우(/ɛhətəroəskˈdést/k/) 균질하다고 가정하면 치우침은 없지만 비효율적인 점 추정과 표준 오차의 치우침 추정으로 이어지며 피어슨 계수에 의해 측정된 적합도를 과대평가할 수 있다.

회귀 분석과 분산 분석의 주요 관심사는 모델링 오류가 모두 동일한 분산을 갖는다고 가정하는 유의성의 통계적 테스트를 무효화하기 때문이다.일반 최소 제곱 추정기는 이질성이 존재하는 경우 여전히 편중되지 않지만, 비효율적이며 ^[4]^[5]대신 일반화 최소 제곱을 사용해야 한다.

이질성은 오류의 두 번째 순간에 대한 예상과 관련이 있기 때문에, 그 존재는 두 번째 ^[6]순서의 오특정이라고 한다.

계량경제학자 로버트 엥글은 이질적 반응(ARC) 모델링 ^[7]기법을 공식화한 이질적 반응 분석 연구로 2003년 노벨 경제학상을 수상했다.

정의.

$y_{i}=x_{i}\beta _{i}+\varepsilon _{i},\ i=1,\ldots ,N,$ i $y_{i}=x_{i}\beta _{i}+\varepsilon _{i},\ i=1,\ldots ,N,$ $y_{i}=x_{i}\beta _{i}+\varepsilon _{i},\ i=1,\ldots ,N,$ $y_{i}=x_{i}\beta _{i}+\varepsilon _{i},\ i=1,\ldots ,N,$ i + $y_{i}=x_{i}\beta _{i}+\varepsilon _{i},\ i=1,\ldots ,N,$ i , $y_{i}=x_{i}\beta _{i}+\varepsilon _{i},\ i=1,\ldots ,N,$ $=$ 1, ... , $y_{i}=x_{i}\beta _{i}+\varepsilon _{i},\ i=1,\ldots ,N,$ , $y_{i}=x_{i}\beta _{i}+\varepsilon _{i},\ i=1,\ldots ,N,$ { $displaystyle$ y _ { $i }$ = x $_$ { i $y_{i}=x_{i}\beta _{i}+\varepsilon _{i},\ i=1,\ldots ,N,$ } \ $varepsilon$ _ { $i$ } , \ $i =$ 1, \ $ldots$ , N $y_{i}=x_{i}\beta _{i}+\varepsilon _{i},\ i=1,\ldots ,N,$ , $displaystyle$ $y _$ i $x_{i}$ } $y_{i}$ $displaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplay$ $y_{i}=x_{i}\beta _{i}+\varepsilon _{i},\ i=1,\ldots ,N,$ $x_{i}$ $y_{i}$ displaystyle $\displaystyle$ \ $varepsilon$ _ ${i}$ 에 $\beta$ $\varepsilon _{i}$ 더해 0을 갖는 랜덤 외란 용어 " $\$ _{i}"를 $지정$ 합니다. $\varepsilon _{i}$ 는 $(\$ _ ${i})$ 의 $\varepsilon _{i}$ 분산이 상수 $\sigma ^{2}$ (\ $displaystyle \sigma$ ^{ $2$ 일 경우 균질성이 됩니다. $\varepsilon _{i}$ $\varepsilon _{i}$ 는 i $({$ 의 $\varepsilon _{i}$ 분산이 i $({style$ i}) $또는$ x $i$ ({ $displaystyle$ ${$ $i$ 의 값에 $따라$ 달라지는 경우 헤테로세사스틱합니다. 예를 들어, $\sigma _{i}^{2}=x_{i}\sigma ^{2}$ $=$ $($ }^{i}) $={i})$ 의 경우 헤테로세사스틱할 수 있습니다.scedastic 함수의 예)이므로 분산은 x $(\displaystyle$ x $x$ 의 $x$ 에 비례합니다.

보다 일반적으로교란 $δ$ $\varepsilon _{i}$ \ $displaystyle$ \ $varepsilon$ _ { $i$ $}$ 의 $\varepsilon _{i}$ $i$ 분산 공분산 행렬이 일정하지 않은 대각선일 경우 교란은 ^[8]헤테로세사스틱이다.아래 행렬은 시간 경과에 걸쳐 관측치가 3개만 있는 경우의 공분산 행렬입니다.행렬 A의 교란은 동질적이다. 이것은 OLS가 최선의 선형 불편 추정기인 단순한 경우이다.행렬 B와 C의 교란은 이질적이다.행렬 B에서는 분산은 시간에 따라 변화하며 시간에 따라 꾸준히 증가합니다.행렬 C에서는 분산은 x $(\displaystyle$ x $x$ 의 $x$ 에 따라 달라집니다.행렬 D의 교란은 대각선 분산이 일정하기 때문에 균질화됩니다. 비록 오프 대각선 공분산은 0이 아니고 일반 최소 제곱은 다른 이유, 즉 직렬 상관 관계가 비효율적이더라도 마찬가지입니다.

디스플레이 스타일A&=\sigma ^{2}{\sigma{bmatrix}1&0\0&1\end{bmatrix}}&B&=\sigma ^{2}{\begin{bmatrix}1&0\0&0\0&2&0&3\\end{bmatrix}&C&=\sigma^{2}x_{1}&0&0&0&0&0&0&0&0&0\0\0&0\x}&0&0&0&0&0&0&0&0&0&0&0\\\\\\\\\\\\\\\cD&=\sigma ^{2}{\sigma{bmatrix}1&\rho ^{2}\rho ^{2}&\rho ^{2}&1\end{bmatrix}}\end{aligned}}

예

이질적 탄성은 관측치의 크기 간에 큰 차이가 있을 때 종종 발생합니다.

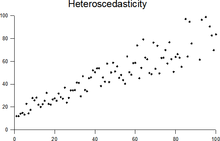
헤테로세타스틱성의 전형적인 예는 소득 대 식비 지출이다.소득이 증가함에 따라 음식 소비의 변동성도 커질 것이다.가난한 사람은 항상 저렴한 음식을 먹음으로써 다소 일정한 양을 소비할 것이다; 부유한 사람은 때때로 저렴한 음식을 사기도 하고 다른 때에는 비싼 음식을 먹기도 한다.고소득층일수록 식료품 소비의 변동성이 크다.
근처에서 로켓이 발사되는 것을 보고 초당 한 번씩 로켓이 이동한 거리를 측정한다고 상상해 보세요.예를 들어, 처음 몇 초 안에 측정값이 가장 가까운 센티미터까지 정확해질 수 있습니다.그러나 5분 후 로켓이 우주로 후퇴할 때 거리 증가, 대기 왜곡 및 기타 다양한 요인 때문에 측정 정확도는 100m까지만 양호할 수 있습니다.수집한 데이터는 이질적인 특성을 보일 수 있습니다.

헤테로세사스틱의 결과

고전적인 선형 회귀 모형의 가정 중 하나는 이질성이 없다는 것입니다.이 가정을 깨는 것은 가우스-마코프 정리가 적용되지 않는다는 것을 의미하며, 이는 OLS 추정기가 Best Linear Unbiased Estimator(BLUE)가 아니며 그 분산이 다른 모든 비편향 추정기 중 가장 낮지 않다는 것을 의미한다.이형성 때문에 일반 최소 제곱 계수 추정치가 편향되지는 않지만, 이형성 때문에 계수의 분산(즉, 표준 오차)에 대한 일반 최소 제곱 계수 추정치가 편향될 수 있습니다. 모집단 분산의 참보다 크거나 작을 수 있습니다.따라서, 이질적 데이터를 사용한 회귀 분석은 예측 변수와 결과 사이의 관계에 대해 여전히 편향되지 않은 추정치를 제공하지만, 표준 오차 및 데이터 분석에서 얻은 추론은 의심스럽다.치우친 표준 오차는 치우친 추론을 초래하므로 가설 검정 결과가 잘못되었을 수 있습니다.예를 들어, OLS가 이질적 데이터 세트에 대해 수행되어 편향된 표준 오차 추정을 산출하는 경우, 연구자는 해당 귀무 가설이 실제 모집단의 특성이 아닌 경우(타입 II 오류를 범함) 주어진 유의성 수준에서 귀무 가설을 기각하지 못할 수 있다.

특정 가정 하에서 OLS 추정기는 적절히 정규화되고 중심화되면(데이터가 정규 분포를 따르지 않는 경우에도) 정규 점근 분포를 가집니다.이 결과는 가설 검정을 수행할 때 정규 분포 또는 카이 제곱 분포(검정 통계량 계산 방법에 따라 다름)를 사용하는 것을 정당화하는 데 사용됩니다.이것은 이질적인 경우에도 유지된다.보다 정확하게는, 이질적 탄성이 존재하는 경우의 OLS 추정기는 적절히 정규화되고 중심화되면 균질적 탄성의 경우와 다른 분산-공분산 행렬을 사용하여 점근적으로 정규적이다.1980년에 White는 OLS 추정기의 ^[2]점근 분포의 분산-공분산 행렬에 대한 일관된 추정기를 제안했다.이 경우 이질성 하에서 OLS 추정기 및 White의 분산-공분산 추정기를 사용하여 가설 검정을 사용할 수 있습니다.

분산 분석 문제에서 ^[9]직면하는 주요 실제 문제이기도 하다.F 테스트는 상황에 ^[10]따라 계속 사용할 수 있습니다.

그러나 계량경제학을 전공하는 학생들은 이질성에 ^[3]과민반응해서는 안 된다고 알려져 왔다.한 저자는 "불균등 오차 분산은 문제가 ^[11]심각할 때만 수정할 가치가 있다"고 썼다.게다가 또 다른 경고 문구는 "헤테로세타스틱성이 다른 ^[3]^[12]좋은 모델을 버릴 이유가 된 적이 없다"는 형식이었다.오차항의 조건부 두 번째 모멘트를 지정하지 않고 추론을 허용하는 헤테로세스틱성 일관성 표준 오차가 등장함에 따라 조건부 균질성 테스트는 ^{[citation needed]}과거처럼 중요하지 않다.

그러나 비선형 모델(예: Logit 및 Probit 모델)의 경우, 이질적인 결과는 더 심각하다. 즉, 모수의 최대우도 추정치(MLE)가 편향될 뿐만 아니라 불일치할 수 있다(우도 함수가 ^[13]이질적인 특성을 정확히 고려하도록 수정되지 않는 한).그러나, 이항 선택 모델(Logit 또는 Probit)의 맥락에서, 이항 선택성은 잘못 지정된 MLE의 점근 평균(즉, 이항 선택성을 ^[14]무시하는 모델)에 양의 스케일링 효과만 초래할 것이다.그 결과, 잘못 지정된 MLE에 기초한 예측은 올바른 상태로 유지됩니다.또한 잘못 지정된 Probit 및 Logit MLE는 점근적으로 정규 분포를 따르므로 (적절한 분산-공분산 행렬을 사용하여) 정규 유의성 검정을 수행할 수 있습니다.그러나 Green이 지적한 바와 같이 일반 가설 검정과 관련하여 "단순히 일관성이 없는 추정치에 대한 강력한 공분산 행렬을 계산한다고 해서 그것이 보상되는 것은 아니다.따라서 이 설정에서 강력한 공분산 행렬의 장점이 ^[15]불분명합니다."

이질성 보정

헤테로세스틱성에 대한 5가지 일반적인 수정이 있습니다.다음과 같은 것이 있습니다.

로그화된 데이터를 봅니다.기하급수적으로 증가하는 비대수 급수는 시간이 지남에 따라 급수가 증가함에 따라 변동성이 증가하는 것으로 보입니다.그러나 백분율 항의 변동성은 다소 안정적일 수 있습니다.
모형에 대해 다른 규격(다른 X 변수 또는 X 변수의 비선형 변환)을 사용합니다.
X 및 Y의 변환 또는 가중치에 OLS를 적용하는 가중 최소 제곱법을 적용합니다.가중치는 일반적으로 변화하는 오차 분산에 따라 관측치에 따라 달라집니다.한 변동에서 가중치는 종속 변수의 크기와 직접 관련이 있으며 이는 최소 제곱율 ^[16]회귀 분석에 해당합니다.
HCSE(Hetheroscedasticity-Consistent Standard Error)는 여전히 편향되어 있지만 OLS ^[2]추정치를 개선합니다.HCSE는 이질성을 갖는 회귀 모형에서 표준 오차의 일관된 추정기입니다.이 방법은 계수 값을 변경하지 않고 이질성을 보정합니다.이 방법은 헤테로세타스틱성이 존재하는 경우 이를 수정하기 때문에 일반 OLS보다 우수할 수 있지만, 데이터가 균질세타스틱일 경우 표준오차는 OLS에 의해 추정된 기존의 표준오차와 동등합니다.뛰어난 유한 표본 특성을 가진 수정으로 헤테로세사스틱 일관성 표준 오차 계산의 화이트 방법의 몇 가지 수정이 제안되었다.
MINQE 또는 일반 ${\textstyle s_{i}^{2}=(n_{i}-1)^{-1}\sum _{j}\left(y_{ij}-{\bar {y}}_{i}\right)^{2}}$ s ${\textstyle s_{i}^{2}=(n_{i}-1)^{-1}\sum _{j}\left(y_{ij}-{\bar {y}}_{i}\right)^{2}}$ 2 ${\textstyle s_{i}^{2}=(n_{i}-1)^{-1}\sum _{j}\left(y_{ij}-{\bar {y}}_{i}\right)^{2}}$ ( ${\textstyle s_{i}^{2}=(n_{i}-1)^{-1}\sum _{j}\left(y_{ij}-{\bar {y}}_{i}\right)^{2}}$ i - ${\textstyle s_{i}^{2}=(n_{i}-1)^{-1}\sum _{j}\left(y_{ij}-{\bar {y}}_{i}\right)^{2}}$ ) - 1 ${\textstyle s_{i}^{2}=(n_{i}-1)^{-1}\sum _{j}\left(y_{ij}-{\bar {y}}_{i}\right)^{2}}$ j ( ${\textstyle s_{i}^{2}=(n_{i}-1)^{-1}\sum _{j}\left(y_{ij}-{\bar {y}}_{i}\right)^{2}}$ - y ${\textstyle s_{i}^{2}=(n_{i}-1)^{-1}\sum _{j}\left(y_{ij}-{\bar {y}}_{i}\right)^{2}}$ ${\textstyle s_{i}^{2}=(n_{i}-1)^{-1}\sum _{j}\left(y_{ij}-{\bar {y}}_{i}\right)^{2}}$ ) $2$ { { $textstyle$ s $_$ { i }^{ } = ( $n$ _ { i }- $1)$ \ $sum$ _ { $j }$ \ $left$ ( $y$ _ $ij$ } - { \ $bary }$ } { $i$ } } ${\textstyle s_{i}^{2}=(n_{i}-1)^{-1}\sum _{j}\left(y_{ij}-{\bar {y}}_{i}\right)^{2}}$ （ $i=1,2,...,k$ ${\textstyle s_{i}^{2}=(n_{i}-1)^{-1}\sum _{j}\left(y_{ij}-{\bar {y}}_{i}\right)^{2}}$ ） 2 ））。 $isplaystyle$ j $=1,2,...,n_{i}$ 개 $j=1,2,...,n_{i}$ )의 경우, 특히 소수의 독립 ^[17]표본에 대해 표본당 관측치 수가 많은 경우( $n_{i}>5$ i $n_{i}>5$ > $n_{i}>5$ \ $displaystyle n_{i} >$ 5 $n_{i}>5$ ） 효율 손실이 크지 않은 경우.

헤테로세스틱

시뮬레이션된 1차 이질적 데이터에 대한 잔차의 절대값

잔차는 독립 변수에 대한 잔차 제곱의 보조 회귀 분석을 수행하는 Breush-Pagan ^[18]검정을 사용하여 균질성을 검정할 수 있습니다.이 보조 회귀 분석에서 설명된 제곱합은 유지되고 2로 나눈 다음 자유도가 독립 ^[19]변수의 수와 동일한 카이 제곱 분포에 대한 검정 통계량이 됩니다.이 카이 제곱 검정의 귀무 가설은 균질성이고 대립 가설은 이질성을 나타냅니다.브루슈-파간 검정은 정규성 또는 작은 표본 크기 이탈에 민감하기 때문에 ^[20]^{[additional citation(s) needed]}Koenker-Bassett 또는 '일반화된 브루슈-파간' 검정이 일반적으로 사용됩니다.보조 회귀 분석에서는 표본 크기에 곱한 R 제곱 값을 유지한 다음 카이 제곱 분포에 대한 검정 통계량이 됩니다(그리고 동일한 자유도를 사용).Koenker-Bassett 검정에는 필요하지 않지만, Breush-Pagan 검정에서는 잔차 제곱합을 표본 크기로 나눈 ^[20]잔차 제곱합으로 나누어야 합니다.그룹별 이질성 테스트는 Goldfeld-Quandt ^[21]테스트를 사용하여 수행할 수 있습니다.

이형성 시험 목록

그룹 간 이질성 테스트는 공식적으로 회귀 모형 내 테스트의 특별한 경우로 간주될 수 있지만, 일부 테스트에는 이 경우에 특정한 구조가 있다.

회귀 검정

그룹화된 데이터 테스트

일반화

균질 분포

두 개 이상의 정규 분포 $N(\mu _{1},\Sigma _{1}),N(\mu _{2},\Sigma _{2}),$ 1, $N(\mu _{1},\Sigma _{1}),N(\mu _{2},\Sigma _{2}),$ 1) $N(\mu _{1},\Sigma _{1}),N(\mu _{2},\Sigma _{2}),$ , $N(\mu _{1},\Sigma _{1}),N(\mu _{2},\Sigma _{2}),$ ( $N(\mu _{1},\Sigma _{1}),N(\mu _{2},\Sigma _{2}),$ 2, $N(\mu _{1},\Sigma _{1}),N(\mu _{2},\Sigma _{2}),$ 2 $N(\mu _{1},\Sigma _{1}),N(\mu _{2},\Sigma _{2}),$ , \ $displaystyle$ N $(\mu _{1}),$ N $(\mu _{2$ },\ $Sigma$ _ ${2})$ 은 $N(\mu _{1},\Sigma _{1}),N(\mu _{2},\Sigma _{2}),$ 동일한 공차 행렬에서 동일한 경우 모두 동종이며 직렬 상관 관계가 없습니다. $}=\Sigma _{2}{sigma},\forall i=$ } 및 $\Sigma _{1}{ii}=\Sigma _{2}{jj},\ \forall i=j.$ 해당 엔트리는 0입니다 $.$ 균질 분포는 통계 패턴 인식 및 기계 학습 알고리즘을 도출하는 데 특히 유용하다.균질성을 가정하는 알고리즘의 인기 있는 예로는 피셔의 선형 판별 분석이 있습니다.균질성의 개념은 ^[25]구상의 분포에 적용될 수 있다.

다변량 데이터

자주성 및 이질성 연구는 스칼라 관측의 분산 대신 벡터 관측의 공분산을 다루는 다변량 사례로 일반화되었다.한 가지 버전은 공분산 행렬을 분산의 다변량 측도로 사용하는 것입니다.몇몇 저자들은 회귀 및 그룹화된 데이터 ^[26]^[27]상황 모두에 대해 이러한 맥락에서 테스트를 고려했다.Bartlett의 그룹화된 데이터 간 이질성 검정은 다변량 사례에 가장 일반적으로 사용되었으며, 다변량 사례에 대해서도 확장되었지만 추적 가능한 솔루션은 두 ^[28]그룹에 대해서만 존재합니다.세 개 이상의 그룹에 대한 근사치가 존재하며 둘 다 Box의 M 검정이라고 합니다.

「」를 참조해 주세요.

레퍼런스

^ 이 용어의 그리스 어원에 대해서는, 을 참조해 주세요.McCulloch, J. Huston (1985). "On Heteros*edasticity". Econometrica. 53 (2): 483. JSTOR 1911250.
^ ^a ^b ^c ^d White, Halbert (1980). "A heteroskedasticity-consistent covariance matrix estimator and a direct test for heteroskedasticity". Econometrica. 48 (4): 817–838. CiteSeerX 10.1.1.11.7646. doi:10.2307/1912934. JSTOR 1912934.
^ ^a ^b ^c Gujarati, D. N.; Porter, D. C. (2009). Basic Econometrics (Fifth ed.). Boston: McGraw-Hill Irwin. p. 400. ISBN 9780073375779.
^ Goldberger, Arthur S. (1964). Econometric Theory. New York: John Wiley & Sons. pp. 238–243. ISBN 9780471311010.
^ Johnston, J. (1972). Econometric Methods. New York: McGraw-Hill. pp. 214–221.
^ Long, J. Scott; Trivedi, Pravin K. (1993). "Some Specification Tests for the Linear Regression Model". In Bollen, Kenneth A.; Long, J. Scott (eds.). Testing Structural Equation Models. London: Sage. pp. 66–110. ISBN 978-0-8039-4506-7.
^ Engle, Robert F. (July 1982). "Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation". Econometrica. 50 (4): 987–1007. doi:10.2307/1912773. ISSN 0012-9682. JSTOR 1912773.
^ 피터 케네디, 계량경제학 가이드, 제5판, 137페이지
^ Jinadasa, Gamage; Weerahandi, Sam (1998). "Size performance of some tests in one-way anova". Communications in Statistics - Simulation and Computation. 27 (3): 625. doi:10.1080/03610919808813500.
^ Bathke, A (2004). "The ANOVA F test can still be used in some balanced designs with unequal variances and nonnormal data". Journal of Statistical Planning and Inference. 126 (2): 413–422. doi:10.1016/j.jspi.2003.09.010.
^ Fox, J. (1997). Applied Regression Analysis, Linear Models, and Related Methods. California: Sage Publications. p. 306. (Gujarati 등).2009년, 페이지 400)
^ Mankiw, N. G. (1990). "A Quick Refresher Course in Macroeconomics". Journal of Economic Literature. 28 (4): 1645–1660 [p. 1648]. doi:10.3386/w3256. JSTOR 2727441.
^ Giles, Dave (May 8, 2013). "Robust Standard Errors for Nonlinear Models". Econometrics Beat.
^ Ginker, T.; Lieberman, O. (2017). "Robustness of binary choice models to conditional heteroscedasticity". Economics Letters. 150: 130–134. doi:10.1016/j.econlet.2016.11.024.
^ Greene, William H. (2012). "Estimation and Inference in Binary Choice Models". Econometric Analysis (Seventh ed.). Boston: Pearson Education. pp. 730–755 [p. 733]. ISBN 978-0-273-75356-8.
^ Tofallis, C (2008). "Least Squares Percentage Regression". Journal of Modern Applied Statistical Methods. 7: 526–534. doi:10.2139/ssrn.1406472. SSRN 1406472.
^ J. N. K. Rao (March 1973). "On the Estimation of Heteroscedastic Variances". Biometrics. 29 (1): 11–24. doi:10.2307/2529672. JSTOR 2529672.
^ Breusch, T. S.; Pagan, A. R. (1979). "A Simple Test for Heteroscedasticity and Random Coefficient Variation". Econometrica. 47 (5): 1287–1294. doi:10.2307/1911963. ISSN 0012-9682. JSTOR 1911963.
^ Ullah, Muhammad Imdad (2012-07-26). "Breusch Pagan Test for Heteroscedasticity". Basic Statistics and Data Analysis. Retrieved 2020-11-28.
^ ^a ^b Pryce, Gwilym. "Heteroscedasticity: Testing and Correcting in SPSS" (PDF). pp. 12–18. Archived (PDF) from the original on 2017-03-27. Retrieved 26 March 2017.
^ Baum, Christopher F. (2006). "Stata Tip 38: Testing for Groupwise Heteroskedasticity". The Stata Journal: Promoting Communications on Statistics and Stata. 6 (4): 590–592. doi:10.1177/1536867X0600600412. ISSN 1536-867X. S2CID 117349246.
^ R. E. Park (1966). "Estimation with Heteroscedastic Error Terms". Econometrica. 34 (4): 888. doi:10.2307/1910108. JSTOR 1910108.
^ Glejser, H. (1969). "A new test for heteroscedasticity". Journal of the American Statistical Association. 64 (325): 316–323. doi:10.1080/01621459.1969.10500976.
^ Machado, José A. F.; Silva, J. M. C. Santos (2000). "Glejser's test revisited". Journal of Econometrics. 97 (1): 189–202. doi:10.1016/S0304-4076(00)00016-6.
^ Hamsici, Onur C.; Martinez, Aleix M. (2007) "구면-균질 분포: 분류에서의 구면분포와 정규분포의 동등성, 기계학습연구저널, 8, 1583-1623
^ Holgersson, H. E. T.; Shukur, G. (2004). "Testing for multivariate heteroscedasticity". Journal of Statistical Computation and Simulation. 74 (12): 879. doi:10.1080/00949650410001646979. hdl:2077/24416. S2CID 121576769.
^ Gupta, A. K.; Tang, J. (1984). "Distribution of likelihood ratio statistic for testing equality of covariance matrices of multivariate Gaussian models". Biometrika. 71 (3): 555–559. doi:10.1093/biomet/71.3.555. JSTOR 2336564.
^ d'Agostino, R. B.; Russell, H. K. (2005). "Multivariate Bartlett Test". Encyclopedia of Biostatistics. doi:10.1002/0470011815.b2a13048. ISBN 978-0470849071.

추가 정보

대부분의 통계교과서는 적어도 일부 균질성과 이질성에 관한 자료를 포함하고 있다.예를 들어 다음과 같습니다.

Asteriou, Dimitros; Hall, Stephen G. (2011). Applied Econometrics (Second ed.). Palgrave MacMillan. pp. 109–147. ISBN 978-0-230-27182-1.
Davidson, Russell; MacKinnon, James G. (1993). Estimation and Inference in Econometrics. New York: Oxford University Press. pp. 547–582. ISBN 978-0-19-506011-9.
Dougherty, Christopher (2011). Introduction to Econometrics. New York: Oxford University Press. pp. 280–299. ISBN 978-0-19-956708-9.
Gujarati, Damodar N.; Porter, Dawn C. (2009). Basic Econometrics (Fifth ed.). New York: McGraw-Hill Irwin. pp. 365–411. ISBN 978-0-07-337577-9.
Kmenta, Jan (1986). Elements of Econometrics (Second ed.). New York: Macmillan. pp. 269–298. ISBN 978-0-02-365070-3.
Maddala, G. S.; Lahiri, Kajal (2009). Introduction to Econometrics (Fourth ed.). New York: Wiley. pp. 211–238. ISBN 978-0-470-01512-4.

외부 링크

Mark Thoma의 YouTube에서의 계량경제학 강의(주제: 헤테로세스틱성)

[1] 이 용어의 그리스 어원에 대해서는, 을 참조해 주세요.McCulloch, J. Huston (1985). "On Heteros*edasticity". Econometrica. 53 (2): 483. JSTOR 1911250.

[White-2] White, Halbert (1980). "A heteroskedasticity-consistent covariance matrix estimator and a direct test for heteroskedasticity". Econometrica. 48 (4): 817–838. CiteSeerX 10.1.1.11.7646. doi:10.2307/1912934. JSTOR 1912934.

[Gujarati-3] Gujarati, D. N.; Porter, D. C. (2009). Basic Econometrics (Fifth ed.). Boston: McGraw-Hill Irwin. p. 400. ISBN 9780073375779.

[4] Goldberger, Arthur S. (1964). Econometric Theory. New York: John Wiley & Sons. pp. 238–243. ISBN 9780471311010.

[5] Johnston, J. (1972). Econometric Methods. New York: McGraw-Hill. pp. 214–221.

[6] Long, J. Scott; Trivedi, Pravin K. (1993). "Some Specification Tests for the Linear Regression Model". In Bollen, Kenneth A.; Long, J. Scott (eds.). Testing Structural Equation Models. London: Sage. pp. 66–110. ISBN 978-0-8039-4506-7.

[7] Engle, Robert F. (July 1982). "Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation". Econometrica. 50 (4): 987–1007. doi:10.2307/1912773. ISSN 0012-9682. JSTOR 1912773.

[8] 피터 케네디, 계량경제학 가이드, 제5판, 137페이지

[9] Jinadasa, Gamage; Weerahandi, Sam (1998). "Size performance of some tests in one-way anova". Communications in Statistics - Simulation and Computation. 27 (3): 625. doi:10.1080/03610919808813500.

[10] Bathke, A (2004). "The ANOVA F test can still be used in some balanced designs with unequal variances and nonnormal data". Journal of Statistical Planning and Inference. 126 (2): 413–422. doi:10.1016/j.jspi.2003.09.010.

[11] Fox, J. (1997). Applied Regression Analysis, Linear Models, and Related Methods. California: Sage Publications. p. 306. (Gujarati 등).2009년, 페이지 400)

[12] Mankiw, N. G. (1990). "A Quick Refresher Course in Macroeconomics". Journal of Economic Literature. 28 (4): 1645–1660 [p. 1648]. doi:10.3386/w3256. JSTOR 2727441.

[13] Giles, Dave (May 8, 2013). "Robust Standard Errors for Nonlinear Models". Econometrics Beat.

[14] Ginker, T.; Lieberman, O. (2017). "Robustness of binary choice models to conditional heteroscedasticity". Economics Letters. 150: 130–134. doi:10.1016/j.econlet.2016.11.024.

[15] Greene, William H. (2012). "Estimation and Inference in Binary Choice Models". Econometric Analysis (Seventh ed.). Boston: Pearson Education. pp. 730–755 [p. 733]. ISBN 978-0-273-75356-8.

[16] Tofallis, C (2008). "Least Squares Percentage Regression". Journal of Modern Applied Statistical Methods. 7: 526–534. doi:10.2139/ssrn.1406472. SSRN 1406472.

[17] J. N. K. Rao (March 1973). "On the Estimation of Heteroscedastic Variances". Biometrics. 29 (1): 11–24. doi:10.2307/2529672. JSTOR 2529672.

[18] Breusch, T. S.; Pagan, A. R. (1979). "A Simple Test for Heteroscedasticity and Random Coefficient Variation". Econometrica. 47 (5): 1287–1294. doi:10.2307/1911963. ISSN 0012-9682. JSTOR 1911963.

[19] Ullah, Muhammad Imdad (2012-07-26). "Breusch Pagan Test for Heteroscedasticity". Basic Statistics and Data Analysis. Retrieved 2020-11-28.

[:1-20] Pryce, Gwilym. "Heteroscedasticity: Testing and Correcting in SPSS" (PDF). pp. 12–18. Archived (PDF) from the original on 2017-03-27. Retrieved 26 March 2017.

[21] Baum, Christopher F. (2006). "Stata Tip 38: Testing for Groupwise Heteroskedasticity". The Stata Journal: Promoting Communications on Statistics and Stata. 6 (4): 590–592. doi:10.1177/1536867X0600600412. ISSN 1536-867X. S2CID 117349246.

[22] R. E. Park (1966). "Estimation with Heteroscedastic Error Terms". Econometrica. 34 (4): 888. doi:10.2307/1910108. JSTOR 1910108.

[23] Glejser, H. (1969). "A new test for heteroscedasticity". Journal of the American Statistical Association. 64 (325): 316–323. doi:10.1080/01621459.1969.10500976.

[24] Machado, José A. F.; Silva, J. M. C. Santos (2000). "Glejser's test revisited". Journal of Econometrics. 97 (1): 189–202. doi:10.1016/S0304-4076(00)00016-6.

[25] Hamsici, Onur C.; Martinez, Aleix M. (2007) "구면-균질 분포: 분류에서의 구면분포와 정규분포의 동등성, 기계학습연구저널, 8, 1583-1623

[26] Holgersson, H. E. T.; Shukur, G. (2004). "Testing for multivariate heteroscedasticity". Journal of Statistical Computation and Simulation. 74 (12): 879. doi:10.1080/00949650410001646979. hdl:2077/24416. S2CID 121576769.

[27] Gupta, A. K.; Tang, J. (1984). "Distribution of likelihood ratio statistic for testing equality of covariance matrices of multivariate Gaussian models". Biometrika. 71 (3): 555–559. doi:10.1093/biomet/71.3.555. JSTOR 2336564.

[28] 'Agostino, R. B.; Russell, H. K. (2005). "Multivariate Bartlett Test". Encyclopedia of Biostatistics. doi:10.1002/0470011815.b2a13048. ISBN 978-0470849071.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

Search

균질성 및 이질성

네임스페이스

더

목차

정의.

예

헤테로세사스틱의 결과

이질성 보정

헤테로세스틱

이형성 시험 목록

회귀 검정

그룹화된 데이터 테스트

일반화

균질 분포

다변량 데이터

「」를 참조해 주세요.

레퍼런스

추가 정보

외부 링크

Search

균질성 및 이질성

정의.

예

헤테로세사스틱의 결과

이질성 보정

헤테로세스틱

이형성 시험 목록

회귀 검정

그룹화된 데이터 테스트

일반화

균질 분포

다변량 데이터

「 」를 참조해 주세요.

레퍼런스

추가 정보

외부 링크

「」를 참조해 주세요.