정규 최소 제곱

시리즈의 일부
회귀 분석
모델
선형 회귀 단순 회귀 다항식 회귀 분석 일반 선형 모형
일반화 선형 모형 개별 선택 이항 회귀 분석 이항 회귀 로지스틱 회귀 분석 다항 로지스틱 회귀 분석 혼합 로짓 프로빗 다항 프로빗 주문된 로짓 순서 프로빗 포아송
다단계 모형 고정 효과 랜덤 효과 선형 혼합 효과 모형 비선형 혼합 효과 모형
비선형 회귀 분석 비모수 반파라메트릭 견고. 양분위수 아이소토닉 주요 컴포넌트 최소 각도 현지의 세그먼트화
변수 오류
견적
최소 제곱 선형 비선형
보통의 가중치 일반화
부분적 총 음이 아닌 능선 회귀 정규화
최소 절대 편차 반복 재중량화 베이지안 베이지안 다변량 최소 제곱 스펙트럼 분석
배경
회귀 검증 평균 및 예측 반응 오차 및 잔차 적합도 학생화 잔차 가우스-마르코프 정리
수학 포털
v t

통계학에서 정규 최소 제곱법(OLS)은 선형 회귀 모형에서 알 수 없는 모수를 추정하기 위한 선형 최소 제곱법의 한 유형입니다.OLS는 주어진 데이터 집합에서 관측된 종속 변수(관측되는 변수의 값)와 독립 변수의 선형 함수에 의해 예측된 변수 사이의 차이의 제곱합을 최소화하는 최소 제곱의 원칙에 따라 설명 변수 집합의 선형 함수 매개변수를 선택한다.

기하학적으로, 이것은 세트의 각 데이터 점과 회귀 표면의 해당 점 사이의 종속 변수의 축과 평행한 거리의 제곱합으로 보여집니다. 차이가 작을수록 모형이 데이터에 더 잘 적합합니다.결과 추정치는 단순한 공식, 특히 회귀 방정식의 오른쪽에 단일 회귀기가 있는 단순한 선형 회귀의 경우 표현될 수 있습니다.

OLS 추정기는 회귀기가 외인성일 때 일관되며, 가우스-마코프 정리에 따르면 오차가 균질적이고 연속적으로 상관되지 않을 때 선형 비편향 추정기 클래스에서 최적이다.이러한 조건에서, OLS 방법은 오차가 유한한 분산을 가질 때 최소-분산 평균-편향 추정치를 제공한다.오차가 정규 분포를 따른다는 추가 가정 하에서 OLS는 최대우도 추정치입니다.

선형 모형

데이터가 n개의$${\$displaystyle$n$\}{\displaystyle {}_{}^{}}$개의 ${\displaystyle {{}_{}}_{}^{}}$ {$x,$ y ${\displaystyle {{}_{}}_{}^{}}$ ${\displaystyle {\mathrm{i}}_{}^{}}$ $=$ ${\displaystyle {}_{}^{}}$ {$display$\$left\{i}_{i}_{$$i=$$1}^n$으로 $구성$되어 있다고 가정합니다. 각 $관측치{\displaystyle }$i에는$$ 스칼라 $응답{\displaystyle {}_{}}$\$displaystyle y_{i}$와 $i$가 포함됩니다$.$$p$ ${\displaystyle$${\displaystyle {{\mathrm{p}}_{}}^{}}$$}$ 파라미터$$$$$($레지스터)의 $hbf$ {$x}$ _${i$}${\displaystyle {}_{}}${${\displaystyle {{}_{}}^{}}$ T$${{$displaystyle \mathbf {x}_{i}=\left[x_i1$},$x_i2},\$displaystyle$,x_ip}\math^{$i}s}s$}s$ {i${\displaystyle {s_{}}^{}}$}의 $오른쪽$입니다.역류기의 이온:

$\displaystyle y_{i}=\varepsilon _{1}+\cdots _{2}+\cdots +\displaystyle _{p}\x_{ip}+\varepsilon _{i}}$

또는 벡터 형태로,

${\displaystyle y_{i}=\mathbf {x} _{i}^{\mathsf {T}}{\boldsymbol {\block }}+\varepsilon _{i},}$

$여기$서 x $i(\$displaystyle $\mathbf {x} _{i$는 앞에서 설명한 바와 같이 모든 설명 변수의 $(\displaystyle$ i$)$$번째$ 관측치 컬럼 벡터입니다$.$times$$})는$$ 알 수 없는 $파라미터$의${\displaystyle }$p$×$${\displaystyle 1_{}}$(\$displaystyle p\times$ 1) $벡터$입니다.$ystyle \varepsilon$ _${i}$는 i$\displaystyle$ i$}$ 관측치의 관측되지 않은 랜덤 변수(예:)를 나타냅니다.$§$ $i$ {$$$displaystyle$ \ $varepsilon$$_${$$i$$$$$$$}$$accounts$ 、 $atorsatorsators$ i i i i i i i x i $이외$의 소스로부터의 $응답$에 대한 영향을 ${\displaystyle {\mathrm{설명}}_{}}$합니다$.$이 모델은 매트릭스 표기법으로도 다음과 같이 쓸 수 있습니다.

${\displaystyle \mathbf {y} = \mathrm {X} {\boldsymbol {\baldsymbol {\varepsilon}},}$

$여기$서 y$(\$$})$ $display$(\displaystyle$\boldsymbol\varepsilon})$는 응답 변수 및$n{\displaystyle }$(\$displaystyle$ n$)$ 관측치의$$ 오류의 n${\displaystyle \times }$${\displaystyle 1}$$(\displaystyle$ n$\times$1) $벡터$이고 X$(\displaystyle$ \$mathrm {X})$는$$n$(\displaystyle$ n)는$$ n)$매트릭스$입니다.설계 매트릭스라고도 불리는 회귀 분석기$.$ i $행$은 x $(\$이며 모든 설명 변수에 $대한{\displaystyle }$ i$(\displaystyle$ i$)$ -th$$ 관측치를 포함합니다.

일반적으로 상수항은 항상 회귀 X $집합($$예$를 들어, $모든{\displaystyle }$ ${\displaystyle \mathrm{i}}$ ${\displaystyle =}$ 1, $…,$ ${\displaystyle n}$ {\$displaystyle$ i$=1,\displaystyle i$$=$1,\display$,n$$\})$에 ${\displaystyle {\mathrm{대해}}_{}}$ x ${\displaystyle 1}$ $=$ 1 {$displaystyle x_$${$i1$}=1$}을 $취함$으로써$$이 회귀에 대응하는$$ $계수{\displaystyle {}_{}}$ ${\displaystyle {\beta \mathrm{}}_{}}$1 {\$displaystylexistyle$ {1} )에 포함됩니다.t.

회귀 분석기가 독립적일 필요는 없습니다. 회귀 분석기 사이에 원하는 관계가 있을 수 있습니다(선형 관계가 아닌 한).예를 들어 어떤 값과 그 제곱에 따라 반응이 선형적으로 달라지는 것으로 의심될 수 있습니다.이 경우 값이 다른 회귀기의 제곱에 불과한 회귀기를 포함시킬 수 있습니다.이 경우 모델은 두 번째 회귀 분석기에서는 2차이지만, 모델이 파라미터에서는 여전히 선형이기 때문에 none-the-less는 선형 모델로 간주됩니다(${\displaystyle \mathit{}}$ $\$

매트릭스/벡터 공식화

지나치게 정해진 시스템을 고려하다

$\displaystyle \sum _{j=1}^{p}X_{ij}\beta _{j}=y_{i},\(i=1,2,\display,n),}$

n중{n\displaystyle}p에서 1차 방정식{p\displaystyle} 알려지지 않은 계수, β 1, β 2,…, n을과β p{\displaystyle \beta_{1},\beta _{2},\dots(_{p}},;p{\displaystyle n> 안 내려}.(참고:위 선형 모델은 X{\displaystyle \mathrm{X}에}모든 요소를 가지고 있다 통보데이터 포인트의 ation.첫 번째 열에는 X ${\displaystyle {\mathrm{i}}_{}}$ 1 $=$(\$displaystyle$ X_${i1$}=$1$이 입력되며, 다른 열에만 실제 데이터가 포함됩니다.$여기$서 p$\displaystyle$p는$$ 퇴행자 수에 1을 더한 값과 같습니다.)이것은 매트릭스 형태로 다음과 같이 쓸 수 있다.

${\displaystyle \mathrm {X} {boldsymbol {\mathbf {y},}$

어디에

${\displaystyle \mathrm{X}={\begin{bmatrix}X_{11}&, X_{12}&, \cdots &, X_{1p}\\X_{21}&, X_{22}&, \cdots, X_{파운드당 2펜스}\\\vdots &, \vdots &, \ddots &, \vdots \\X_{n1}& &, X_{n2}&, \cdots &, X_{np}\end{bmatrix}},\qquad}{\boldsymbol{\beta}={\begin{bmatrix}\beta _{1}\\\beta _{2}\\\vdots(_{p}\end{bmatrix}},\qquad\mathbf{y}.={\begin{bmatrix}y_{1}\\y_{2}\\\vdots \\y_{n}\end {bmatrix}.}$

이러한 시스템은 대개 정확한 해법을 가지고 있지 않으므로, 목표는 2차 최소화 문제를 푸는 의미에서 "최적" 방정식에 맞는 $계수{\displaystyle \mathit{}}$β(\$displaystyle\boldsymbol\beta })$를 찾는 것이다.

$(\displaystyle {\boldsymbol {\operatorname {\in}}), S(\boldsymbol {\symbol})= 언더셋(\boldsymbol {\in}}})$

여기서 S$(\displaystyle$ S$)$의 목적 $함수$는 다음과 같습니다.

$({displaystyle S({\boldsymbol {\boldsymbol {\i}})=\sum _{i=1}-\sum _{j=1}X_{ij}\beta _{j}{2}{\biggr}^{2}=boldy {\}\mathbald}{mathby {\m}{x}{x}{mathbold}{n}{x}{\m}{\m}{\mathbold}{\m}{\m}{\m}{{{}$

이 기준을 선택하기 위한 정당성은 아래 속성에서 확인할 수 있습니다.$행렬{\displaystyle \mathrm{}}$ X의 $p열$$(\${X$$$})$이 정규 방정식을 풀어서 선형 독립적일 경우, 이 최소화 문제는 고유한 해결 방법을 가지고 있다.

${\displaystyle(\mathrm {X} ^{\mathsf {T}}\mathrm {X} =\mathrm {X} ^{\mathsf {T}}\mathbf {y} \}$

$행렬{\displaystyle {\mathrm{}}^{}}$ ${\displaystyle {\mathsf{}}^{}}$ $(\$는 그램 행렬, $행렬{\displaystyle {\mathrm{}}^{}}$ ${\displaystyle {\mathsf{}}^{}}$ T$$(\$displaystyle \mathrm {X} ^{\mathsf${$T}}}\mathbf {y}$ })^[1]는$$ 회귀 분석자에 의한 모멘트 행렬로 알려져 있습니다.$마지막$으로 β$^$ {$displaystyle${\$hat {boldsymbol {beta }}}$은 최소 제곱 하이퍼플레인의 계수 벡터이며, 다음과 같이 표현됩니다.

${\displaystyle {\hatsymbol {\mathrm {X} =\left(\mathrm {T} ^{-1}\mathrm {X} ^{\mathsf {T}} ^{\mathbf {y}}} } }$

또는

${\displaystyle {\hotsymbol {\top}=\mathbf {X}^{-1}\mathbf {X}^{\top}{\boldsymbol {varepsilon}}}+(\mathbf {X}}$

견적

b가 매개변수 벡터 β의 "후보" 값이라고 가정합니다.i번째 관측치의 잔차라고 하는 y_i - xb_i^T 양은 데이터 점(x_i, y_i)과 초평면 y = xb^T 사이의 수직 거리를 측정하여 실제 데이터와 모형 간의 적합도를 평가합니다.잔차 제곱합(SSR)(오차 제곱합(ESS) 또는 잔차 제곱합(RSS)^[2]이라고도 함)은 전체 모형 적합치에 대한 측도입니다.

${\displaystyle S(b)=\sum _{i=1}^{n}(y_{i}-x_{i}^{\mathrm {T}}b)^{2}=(y-Xb)^{\mathrm {T}}(y-Xb)},}$

여기서 T는 전치 행렬을 나타내며, 종속 변수의 특정 값과 관련된 모든 독립 변수의 값을 나타내는 X의 행은 X = x이다_ii^T.이 합계를 최소화하는 b의 값을 β의 OLS 추정기라고 합니다.함수 S(b)는 양의 제곱 Hessian과 함께 b에서 2차이므로, 이 ${\displaystyle 함수}$는 b${\displaystyle \stackrel{}{}=}$ β $^$ {$style$ b =$qr hat$ {\$display$ $\}\}$에서 고유한 전역 최소값을 가지며, 이는 명시적 ^[3][proof]공식으로 나타낼 수 있다.

${\displaystyle {\hat}=\operatorname {n}_{b\in \mathbb {R}^{p}}S(b)=(X^{\mathrm {T}}X)^{\mathrm {T}}Y\}}$

곱 N^T=X X는 그램 행렬이며, 역행렬 Q=N은^–1 공분산 행렬 C와_β 밀접하게 관련된 ^[4][5][6]β의 보조인자 행렬이다.행렬^T (X^TT X)^–1 X=Q X는 X의 무어-펜로즈 유사 역행렬이라고 불린다.이 공식은 설명 변수 사이에 완벽한 다중 공선성이 없는 경우에만 추정을 수행할 수 있다는 점을 강조합니다(그람 행렬에 역행렬이 없는 경우).

추정된 β를 얻은 후 회귀의 적합치(또는 예측치)는 다음과 같습니다.

${\displaystyle {y}=X{\hat}=Py,}$

여기서 P = X(XX^T)⁻¹X는^T X의 열에 걸쳐 있는 공간 V에 대한 투영 행렬이다.이 행렬 P는 변수 y 위에 "모자를 놓기" 때문에 해트 행렬이라고도 합니다.P와 밀접하게 관련된 또 다른 행렬은 전멸기 행렬 M = I_n - P이다. 이것은 V와 직교하는 공간에 투영 행렬이다.행렬 P와 M은 모두 대칭이고 아이덴포텐트(P² = P 및 M² = M)이며 동일성 PX = X 및 MX = ^[7]0을 통해 데이터 행렬 X와 관련됩니다. 행렬 M은 회귀 분석에서 잔차를 생성합니다.

$(\displaystyle {\hat {y}}=y-{\hat {y}}=My=M(X\beta +\varepsilon)=(MX)\beta +M\varepsilon=M\varepsilon.$

이러한 잔차를 사용하여 축소 카이 제곱 통계량을 사용하여 θ의 ² 값을 추정할 수 있습니다.

${{displaystyle s^{2}=hat {\hat {{varepsilon}}^{\mathrm {T}}{n-p}}=hat frac {{\mathrm {T}}{{n-p}}=hat frac {y}{\mathrm {T}}{{\mathrm}}}{M}}}}{{{\mathrm}}}}}}}}}}M}}{{\mathfrac {\m}}}}}}}}}}}}}}}$

분모인 n-p는 통계적 자유도이다.첫 번째 수량² s는 ,의² OLS 추정치이고, 두 번째 수량 $(\$는$$σ의² MLE 추정치입니다.두 추정치는 큰 표본에서 매우 유사합니다. 첫 번째 추정치는 항상 치우침이 없는 반면 두 번째 추정치는 치우침이 있지만 평균 제곱 오차가 더 작습니다.실제로² s는 가설 검정에 더 편리하기 때문에 더 자주 사용됩니다.s의² 제곱근을 회귀 표준 오차,^{[8] [9][10]}회귀 표준 오차 또는 ^[7]방정식의 표준 오차라고 합니다.

일반적으로 X로 회귀하여 표본의 초기 변동을 얼마나 줄일 수 있는지를 비교하여 OLS 회귀 분석의 적합도를 평가합니다.결정² 계수 R은 종속 변수 y의 "총" 분산에 대한 "설명된" 분산의 비율로 정의되며, 회귀 제곱합이 ^[11]잔차 제곱합과 동일한 경우 다음과 같습니다.

${\displaystyle R^{2}=subfrac {\hat {y}_{i}-{\overline {y}}^{2}}=subfrac {y^{\mathrm {T}}P^{\mathrm {T}\mathrm {Y}LP}LP}LP {\mathrac {\y} {\}$

여기서 TSS는 종속 변수에 대한 총 제곱합이고, $L$ $=$ $I_{}n\frac{\mathrm{}}{}$ - 1 $\frac{n}{}$ $J_{}$n n n { \ $textstyle$ L = $I$_ { n } - { \$frac$ {1} {$n$} J _ { $n$} $where{}_{}$ $、$ J $n_{}$ \ $textstyle$ J _ { $n$} is$$ 1 of 。( $\displaystyle$L은 상수$$ 회귀에 해당하는 중심 행렬로, 변수에서 평균을 빼기만 하면 됩니다.)R에 의미가 있으려면² 회귀 절편이 계수인 상수를 나타내는 1의 열 벡터가 회귀 분석기의 행렬 X에 포함되어 있어야 합니다.이 경우 R은 항상² 0과 1 사이의 숫자이며, 1에 가까운 값은 양호한 적합도를 나타냅니다.

종속 변수의 함수로서의 독립 변수 예측의 분산은 다항식 최소 제곱 기사에 나와 있습니다.

단순 선형 회귀 모형

데이터 행렬 X에 상수와 스칼라 회귀 분석기_i x의 두 변수만 포함된 경우 이를 "단순 회귀 모형"^[12]이라고 합니다.이 경우는 수동 계산에 적합한 훨씬 더 간단한 공식을 제공하기 때문에 초보 통계 클래스에서 종종 고려됩니다.파라미터는 일반적으로 (α, β)로 표시됩니다.

$\displaystyle y_{i}=\alpha +\display x_{i}+\varepsilon _{i}.}$

이 경우 최소 제곱 추정치는 간단한 공식으로 제공됩니다.

${\displaystyle {\hat} {\hat} {\hat} {\sum {x_i} {x_{i}} {{n} {{n} - (\sum {x_{i} {i}} {{2}} - (\sum {x_{i} {{2}} {\hat =} overline} } }$

대체 파생상품

이전 섹션에서는 최소 제곱 $추정기{\displaystyle \stackrel{}{}}$β $^$ {$displaystyle${\$hat {\$beta }}을$($를) 모델의 잔차 제곱 합계를 최소화하는 값으로 구했다.그러나 다른 접근법에서 동일한 추정치를 도출하는 것도 가능하다.모든 경우 OLS 추정기의 공식은 β = (XX^T)⁻¹Xy로^T 동일하다. 유일한 차이점은 이 결과를 해석하는 방법이다.

투영

이 섹션은 청소가 필요할 수 있습니다.선형 최소 제곱(수학)에서 병합되었습니다.

수학자들에게 OLS는 지나치게 결정된 선형 방정식 Xβ δ y의 대략적인 해이다. 여기서 β는 미지의 것이다.시스템을 정확하게 풀 수 없다고 가정할 때(방정식 n의 수가 미지의 p의 수보다 훨씬 크다), 우리는 오른쪽과 왼쪽 사이에 최소한의 불일치를 제공할 수 있는 해결책을 찾고 있다.바꿔 말하면, 델은, 델이 고객의 요구를 만족시킬 수 있는 솔루션을 찾고 있습니다.

${\displaystyle {\hat } = min _{\display} ,\lVert y-X\beta \rVert ,}$

여기서 ·는 n차원 유클리드 공간ⁿ R의 표준² L 노름이다.예측된 양 Xβ는 퇴행 벡터의 특정 선형 조합일 뿐입니다.따라서, 잔차 벡터 y - Xβ는 X의 열에 의해 가로놓인 선형 부분 공간에 y가 직교로 투영될 때 가장 작은 길이를 갖게 된다.이 경우 OLS $추정기{\displaystyle \stackrel{}{}}$β $^$ {style {\$hat }$은 X를 기준으로 y = Py의 벡터 분해 계수로 해석할 수 있다.

즉, 최소 구배 방정식은 다음과 같이 쓸 수 있습니다.

$(\displaystyle(\mathbf {y} - X{\hat\boldsymbol {\hat})^{\rm {T}}X=0).}$

이러한 방정식의 기하학적 해석은 점곱${\displaystyle (}$y${\displaystyle }$- ${\displaystyle X\stackrel{}{}}$$^$ \$displaystyle$ $\mathbf {y} -X{\hat$$$\${\displaystyle bold\stackrel{}{\mathit{}}}$ symbol }}}${\displaystyle \mathrm{x<img\; alt="\backslash mathbf\; \{y\}\; -X\{\backslash hat\; \{\backslash boldsymbol\; \{\backslash beta\; \}\}\}"\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/d28701ed83da946fc9829429e8a174f3623ef1e1"\; style="vertical-align:\; -0.671ex;\; width:7.802ex;\; height:3.176ex;">}}$ ${\displaystyle X\mathbf{}}$ v$$- $displaystyle (\mathb {y$$^})$이므로 잔차 $벡터$가 X의 열 공간과 직교한다는 것이다$.$모든 등각 벡터 v에 대해 0이 됩니다.즉${\displaystyle ,}$ y - ${\displaystyle X\stackrel{\mathbf{}}{\mathit{}}}$β $^$ { $displaystyle$$$\ $mathbf${$$$y$} - $X$$${ \ bold $symbol$${$ \ $hat$$\}\}\}$는 가능한 모든 $벡터{\displaystyle \mathbf{}}$y - ${\displaystyle X\mathit{}}$β 중 가장 짧으며, 즉 잔차 $분산$이 최소임을 $의미$합니다.이것은 오른쪽에 예시되어 있습니다.

행렬 $]([X\K])$이 비변형이고 K^T= 0(cf)이라는 가정 하에 $^$과 행렬 K(\displaystyle)를 소개합니다.직교 투영) 잔차 벡터는 다음 방정식을 충족해야 합니다.

${\displaystyle {\mathbf {r}}\mathbf {y}=K{\hat {\boldsymbol {r}}.}$

선형 최소 제곱의 방정식과 해는 다음과 같이 설명된다.

${\displaystyle \mathbf {y} = bgin {bmatrix} X&K\end {bmatrix} {\begin {pmatrix} {\hat {\boldsymbol {pmatrix}} {\hat {\boldsymbol } }$

${\displaystyle {\boldsymbol {pmatrix}\hat {boldsymbol {pmatrix}\end{pmatrix}={begin {bmatrix}X&K\end{bmatrix}{-1}\mathbf {y} =bgenbegin{bmatrix}{\rmatrix}{{{\rm}{T}$

또 다른 방법은 회귀선을 데이터 ^[13]집합의 두 점의 조합을 통과하는 선의 가중 평균으로 간주하는 것입니다.이 계산 방식은 계산 비용이 더 많이 들지만 OLS에 대한 더 나은 직관을 제공합니다.

최대우도

OLS 추정기는 오차항에 ^[14][proof]대한 정규성 가정에서의 최대우도 추정기(MLE)와 동일합니다.이 정규성 가정은 Yule과 ^{[citation needed]}Pearson의 선형 회귀 분석에서 초기 연구의 기초를 제공했기 때문에 역사적으로 중요합니다.MLE의 특성으로부터 정규성 가정이 ^[15]충족될 경우 OLS 추정기가 점근적으로 효율적이라고 추론할 수 있다(분산에 대한 크라메르-라오 한계를 달성한다는 의미).

일반화된 모멘트 방법

iid의 경우, OLS 추정기는 모멘트 조건에서 발생하는 GMM 추정기로도 볼 수 있다.

$\displaystyle \mathrm {E} {big [},x_{i}(y_{i}-x_{i}^{T}\beta}, {\big }=0.}$

이러한 모멘트 조건은 회귀 분석기가 오류와 상관되지 않아야 함을 나타냅니다.x는 p벡터이므로_i 모멘트 조건의 수는 파라미터 벡터β의 치수와 같기 때문에 시스템이 정확하게 식별된다.이것은 추정기가 가중치 행렬의 선택에 의존하지 않는 이른바 고전 GMM 사례이다.

원래의 엄밀한 외형성 가정_i E[color_i x] = 0은 위에 언급된 것보다 훨씬 풍부한 모멘트 조건 집합을 의미한다.특히, 이 가정은 벡터 함수 θ에 대하여, 모멘트 조건 E[colon(x_i)·colon_i] = 0이 유지된다는 것을 의미한다.그러나 가우스-마코프 정리를 사용하여 함수 θ의 최적 선택은 위에 게시된 모멘트 방정식의 결과를 가져오는 θ(x) = x를 취하는 것이라는 것을 보여줄 수 있다.

특성.

전제 조건

OLS 기술을 적용하기 위해 선형 회귀 모델을 주조할 수 있는 몇 가지 다른 프레임워크가 있습니다.이러한 각 설정은 동일한 공식과 결과를 생성합니다.유일한 차이점은 방법이 의미 있는 결과를 제공하기 위해 부과해야 하는 해석과 가정이다.적용 가능한 프레임워크의 선택은 주로 수중에 있는 데이터의 특성과 수행해야 하는 추론 작업에 따라 결정된다.

해석의 차이선 중 하나는 회귀 분석기를 랜덤 변수로 처리할지 아니면 미리 정의된 상수로 처리할지 여부입니다.첫 번째 경우(랜덤 설계)에서는 관측 연구처럼 회귀 변수_i x가 랜덤이며 일부 모집단의 y와_i 함께 표본 추출됩니다.이 접근방식을 통해 추정기의 점근적 특성을 보다 자연스럽게 연구할 수 있습니다.다른 해석(고정 설계)에서는 회귀 분석기 X가 설계에 의해 설정된 알려진 상수로 처리되고 Y는 실험에서와 같이 X의 값에 대해 조건부로 표본 추출됩니다.X를 조건으로 추정과 추론이 이루어지기 때문에 실질적인 목적상 이 구별은 종종 중요하지 않다.이 기사에 기재되어 있는 모든 결과는 랜덤 설계 프레임워크 내에 있습니다.

고전적 선형 회귀 모형

고전적 모형은 "확정 표본" 추정 및 추론에 초점을 맞춥니다. 즉, 관측치 수 n이 고정됨을 의미합니다.이것은 OLS의 점근 거동을 연구하고 관측치의 수가 무한대로 증가할 수 있는 다른 접근법과 대조된다.

• 올바른 사양.선형 함수 형식은 실제 데이터 생성 프로세스의 형식과 일치해야 합니다.
• 엄격한 이질성.회귀 분석의 오류에는 조건부 평균 ^[16]0이 있어야 합니다.

  $\displaystyle \operatorname {E} [,\varepsilon \mid X,]= 0.}$

이질성 가정의 직접적인 결과는 오차의 평균 0입니다.E[disc] = 0이며 회귀기는 오류와 관련이 없습니다.E[XX^T] = 0 。

이질성 가정은 OLS 이론에 매우 중요하다.이 값이 유지되면 회귀 변수를 외부 발생 변수라고 합니다.그렇지 않으면 오차항과 상관된 회귀를 ^[17]내생성이라고 하며 OLS 추정기가 편향됩니다.이러한 경우, 계측 변수의 방법을 사용하여 추론을 수행할 수 있다.

• 선형 종속성이 없습니다.X의 회귀 분석기는 모두 선형 독립적이어야 합니다.즉, 수학적으로 행렬 X의 열 순위는 거의 확실하게 ^[18]완전해야 합니다.

  $\displaystyle \Pr \!{\big [},\operatorname {rank}(X)=p,{\big }=1.}$

일반적으로 회귀기는 적어도 두 번째 순간까지 유한한 모멘트를 갖는다고 가정합니다.그러면_xx 행렬 Q = E[XX^T / n]는 유한하고 양의 반정렬이다.

이 가정이 위반되면 회귀기를 선형 종속 또는 완전히 다중 공선이라고 합니다.이 경우, 동일한 선형 의존 서브스페이스에 있는 회귀기의 새로운 값에 대해 y값의 예측은 여전히 가능하지만 회귀 계수 β의 값을 학습할 수 없다.

• 구면 오차:^[18]

  $\{Var} X}\displaystyle \operatorname {Var} [,\varepsilon \mid X,]=\sigma ^{2}I_{n},$

여기서_n I는 차원 n의 항등 행렬이고 θ는² 각 관측치의 분산을 결정하는 매개변수입니다.이 θ는² 모형에서 불필요한 모수로 간주되지만 일반적으로 추정되기도 합니다.이 전제를 위반했을 경우, OLS의 견적은 유효하지만, 효율은 떨어집니다.

이 전제는 다음 두 부분으로 분할하는 것이 일반적입니다.

• 균질성:E [ ε_i² X ] = σ², 오차항의 분산이² 각 관측치에서 동일함을 의미합니다.이 요건이 위반되면 이를 헤테로세사스틱이라고 하며, 이 경우 보다 효율적인 추정치는 가중 최소 제곱이 될 것이다.오차가 무한 분산인 경우 OLS 추정치도 무한 분산이 됩니다(단, 오차의 평균이 0인 한 큰 수의 법칙에 따라 오차가 참 값으로 이동하지만).이 경우 강력한 추정 기법을 사용하는 것이 좋습니다.
• 자기 상관 없음: 오차는 관측치 간에 상관되지 않습니다.E [ " X_ij ] = i i j의 경우 0 。이 가정은 시계열 데이터, 패널 데이터, 군집 표본, 계층 데이터, 반복 측정 데이터, 세로 데이터 및 종속성이 있는 기타 데이터의 맥락에서 위반될 수 있습니다.이러한 경우 일반화 최소 제곱은 OLS보다 더 나은 대안을 제공합니다.자기 상관의 또 다른 표현은 직렬 상관입니다.

• 정상.또한 오차가 ^[19]회귀기에 따라 정규 분포를 갖는다고 가정할 수 있습니다.

  $\ \ { (^{displaystyle \varepsilon \mid X\sim {N}) (0,\sigma ^{2})I_{n}).}$

이러한 가정은 OLS 방법의 타당성을 위해 필요하지 않지만, 그러한 경우에 특정 추가 유한 표본 속성을 설정할 수 있다(특히 가설 테스트 영역에서).또한 오차가 정규인 경우 OLS 추정기는 최대우도 추정기(MLE)와 같으므로 모든 정규 추정기 클래스에서 점근적으로 효율적입니다.중요한 것은 정규성 가정이 오차항에만 적용된다는 것입니다. 일반적인 오해와 달리 반응(의존성) 변수를 정규 ^[20]분포를 따를 필요는 없습니다.

독립적이고 균등하게 분산된(iid

일부 애플리케이션, 특히 단면 데이터의 경우, 모든 관측치가 독립적이고 균등하게 분포되어 있다는 추가 가정이 적용됩니다.즉, 모든 관측치는 랜덤 표본에서 추출되므로 앞에서 설명한 모든 가정을 더 쉽고 쉽게 해석할 수 있습니다.또한 이 프레임워크는 점근적 결과(샘플 크기 n → θ)를 진술할 수 있게 해주며, 이는 데이터 생성 프로세스에서 새로운 독립적 관측치를 가져올 수 있는 이론적 가능성으로 이해된다.이 경우의 전제 조건은 다음과 같습니다.

• iid 관측치: (x_i, y_i)는 모든 i µ j에 대해 (x_j, y_j)와 독립적이며 동일한 분포를 가진다.
• 완벽한 다중 공선성 없음: Q_xx = E [ x_i x_i^T ]는 양의 행렬이다.
• 이질성:E[ ε_ii x ] = 0;
• 균질성:Var [ x_ii² x ]= 。

• 확률 프로세스 {x_i, y_i}은(는) 정상이고 에르고딕입니다. {x_i, y_i}이(가) 비정상인 경우 {x_i, y_i}이(^[21]가) 공적분하지 않는 한 OLS 결과는 종종 거짓입니다.
• 역류기는 미리 정해져 있습니다.모든 i = 1, ..., n에 대해 E[xθ_ii] = 0;
• p×p 행렬_xx Q = E [ x_ii^T x ]는 완전 등급이며, 따라서 양의 행렬이다.
• {x_ii}}은 2차 모멘트_xxε² Q = E[xx_i²_ii^T x ]의 유한 행렬을 갖는 마티게일 차분 수열이다.

샘플

우선 엄격한 외부성 가정 하에서 OLS $추정기{\displaystyle \stackrel{}{}}$β $^$ \$displaystyle \scriptstyle \hat \hat$ \beta $}$ 및 s는² 편견이 없으며,^[22][proof] 이는 기대값이 매개변수의 실제 값과 일치함을 의미한다.

${\displaystyle \operatorname {E} [, {hat {}\mid X,}=\beta,\display \operatorname {E}[,s^{2}\mid X,]=\sigma ^{2}}}$

엄격한 외부성이 유지되지 않는 경우(많은 시계열 모델의 경우와 같이 외부성은 과거의 충격에만 대해 가정하고 미래의 충격은 가정하지 않는 경우), 이러한 추정치는 유한 표본에 편향될 것이다.

β$^$ { $displaystyle \scriptstyle \hat${ $beta }}$의 분산-공분산 행렬(또는 단순 공분산 행렬)은 다음과 같다^[23].

${\displaystyle \operatorname {Var} [,\hat {hat }\mid X,]=\sigma ^{2}(X^{T}X)^{-1}=\sigma ^{2}Q.}$

특히 각 $계수\beta {\displaystyle {\stackrel{}{}}_{}}$^ ${\displaystyle j_{}}$\$displaystyle \scriptstyle \hat {beta$}_${j}$의 표준 오차는 이 행렬의 j번째 대각 요소의 제곱근과 같습니다.이 표준오차의 추정치는 미지의 수량 θ를² 추정치² s로 대체하여 구한다.따라서,

$hat {j2}({jj.}}({\hat {hat }_{j}={s^{2}(X^{T}X)_{j}^{-1})$

또한 $추정기{\displaystyle \stackrel{}{}}$β $^$ {$displaystyle \scriptstyle \hat {beta }}$이(^[23]가) 모델의 잔차와 관련이 없음을 쉽게 알 수 있다.

${\displaystyle\operatorname{Cov}[,\hat,{\hat\varepsilon}}}\mid X} = 0.}$

가우스-마코프 정리는 구면 오차 가정(즉, 오차는 상관없고 균질적이어야 함)에서 $추정기{\displaystyle \stackrel{}{}}$β$$^$displaystyle$ \$scriptstyle {\$hat {$beta$}}이$$ 선형 비편향 추정기 클래스에서 효율적이라고 말한다.이를 최적 선형 불편 추정기(BLUE)라고 합니다.효율은 마치 다른 $추정치\beta {\displaystyle \stackrel{}{}}$ $~\$를 찾는$$ 것처럼 이해해야 합니다.그러면 y는 선형이고 편향되지 않습니다.

${\}\ X}\ X 0}{\displaystyle \operatorname {Var} [,\tilde }$

이것은 음이 아닌 역행렬이라는 의미에서요.이 정리는 선형 비편향 추정기의 클래스에서만 최적성을 확립하며, 이는 상당히 제한적이다.오차항 ,의 분포에 따라 다른 비선형 추정기가 OLS보다 더 나은 결과를 제공할 수 있습니다.

이라고 가정하다

지금까지 열거된 속성은 오차항의 기본 분포에 관계없이 모두 유효합니다.그러나 정규성 가정(즉, θ ~ N(0, θI²_n))이 유지된다고 가정할 경우 OLS 추정기의 추가 속성을 나타낼 수 있습니다.

$추정기{\displaystyle \stackrel{}{}}$β $^$ $displaystyle \scriptstyle \hat \beta }$은(^[24]는) 다음과 같이 평균과 분산을 사용하여 정규 분포를 따릅니다.

$\sigma ^{big}}}{\displaystyle {\sim\mathcal {N}{\be}}{\mathcal {n}, \sigmata ^{{{{{{{}}}}}}}}, {gmatha ^{bigmata } {gmathcm}}}$

여기서 Q는 보조 요인 행렬입니다.이 추정치는 모델에 대한 Cramér-Rao 경계에 도달하므로 모든 편향되지 않은 추정치의 클래스에 ^[15]최적이다.가우스-마코프 정리와는 달리, 이 결과는 선형 및 비선형 추정기 사이의 최적성을 확립하지만 정규 분포 오차항의 경우에만 성립한다는 점에 유의한다.

추정기² s는 카이 제곱 ^[25]분포에 비례합니다.

$s\\ _}{\displaystyle s^{2}\sim\{frac\{n-p}\cdot\chi_{n-p}^2}$

이 추정치의 분산은 2µ⁴/(n - p)이며, 이는 크라메르-라오 한계⁴ 2µ/n에 도달하지 않는다.그러나 추정기^{2 [26]}s보다 분산이 작은 θ의² 편향되지 않은 추정기는 없는 것으로 나타났다.이 수업에서 만약 우리가, 그리고 estimators의 모델의 모눈 잔차(레이더 초계 잠수함)의 합에 비례하는 수업을 고려해 편향된 estimators 수 있도록 기꺼이 허락해 최고의(평균 제곱 오차의 의미에서)추정자만 한 regressor(우편은 이 Cramér–Rao 경우 묶어서 밤새도록 애타게 바라지.)2차 감시 레이더/(n− p+2),~σ2 것이다 =^[27] 1)

또한 $추정치{\displaystyle \stackrel{}{}}$β $^$ \$displaystyle \scriptstyle \hat \hat$ \beta² $}$ 및 ^[28]s는 독립적이므로 회귀 분석을 위한 t- 및 F-검정을 구성할 때 유용합니다.

있는

앞에서 설명한 바와 같이 $추정기{\displaystyle \stackrel{}{}}$β $^$ {\$displaystyle {\hat$ {$beta }}$은 y로 선형이며, 이는 종속 변수_i y의 선형 조합을 나타냅니다.이 선형 조합의 가중치는 회귀 분석기 X의 함수이며 일반적으로 동일하지 않습니다.가중치가 높은 관측치는 추정기 값에 더 뚜렷한 영향을 미치기 때문에 영향력 있는 관측치라고 합니다.

어떤 관측치가 영향을 미치는지 분석하기 위해 특정 j번째 관측치를 제거하고 추정 수량이 얼마나 변할지를 고려합니다(잭나이프 방법과 유사).β에 대한 OLS 추정기의 변화는 다음과 같을 것이다.

${\}{{j}}{\}{display {\hat$

여기서_j h = x_j^T (XX^T)⁻¹x는_j 햇 행렬 P의 j번째 대각 원소이고_j x는 j번째 관측치에 해당하는 회귀체의 벡터이다.마찬가지로, 데이터 집합에서 해당 관찰을 생략한 결과로 발생하는 j번째 관찰에 대한 예측 값의 변경은 다음과 같습니다.

$hat{displaystyle {y}-{j}^{\displaystyle {y}=x_{j}{j}{{\mathrm}{j}}}{{\mathrm}}}{{{t}}}}}}{{\m}}}}}}{\mathrm}}}{{{{{\m}T}{\hat {h}=-{\frac {h_{j}}{1-h_{j}},{\hat {varepsilon}}_{j}}$

모자 행렬의 특성에서 0 µh_j ≤ 1로, 합계가 p가 되어 평균_j h µp/n이 됩니다.이러한 양_j h를 레버리지라고 하며 h가 높은_j 관측치를 레버리지 ^[30]점이라고 합니다.일반적으로 레버리지가 높은 관측치는 오류나 특이치 또는 다른 방식으로 데이터 집합의 나머지 부분과 다른 경우에 더 주의 깊게 조사해야 한다.

(분할 회귀)

될 수 .

$y_{_{displaystyle y=X_{1}\beta _{2}\beta _{2}+\varepsilon,}$

여기서₁ X와₂ X는 n×p₁, n×p₂ 및₁ β를 가지며₂, β는 p₁×1 및₂ p×1 벡터이며, p₁ + p₂ = p이다.

Frisch-Waugh-Lovell 정리에 따르면 이 회귀 분석에서 $^{$$${\hat {\$varepsilon$}}과 OLS $추정치{\displaystyle {\stackrel{}{}\beta }_{\mathrm{}}}$ ^$$2(\$displaystyle$ \$scriptstyle {\hat }}}$_$${$2})$는 다음과 같은 ^[31]회귀 분석에서 잔차₂ 및 OLS 추정치와 수치적으로 동일하다.

$displaystyle M_{1}y=M_{1}X_{2}+\eta,}$

여기서₁ M은 회귀기₁ X에 대한 소멸기 행렬입니다.

그 정리는 많은 이론적 결과를 확립하는 데 사용될 수 있다.예를 들어, 상수 및 다른 회귀 분석기가 있는 회귀 분석을 갖는 것은 종속 변수 및 회귀 분석기에서 평균을 뺀 다음 상수 항 없이 평균 제거 변수에 대해 회귀 분석을 실행하는 것과 같습니다.

견적

방정식의 합니다.

$A Qdisplaystyle A\colon\colon Q^{T}\beta =c,})$

여기서 Q는 풀랭크의 p×q 행렬이고, c는 알려진 상수의 q×1 벡터이다.여기서 q < p.이 경우 최소 제곱 추정은 제약 조건 A가 적용되는 모형의 잔차 제곱 합계를 최소화하는 것과 같습니다.구속된 최소 제곱(CLS) 추정치는 다음과 같은 명시적 ^[32]공식으로 나타낼 수 있습니다.

${\}^{^{Big1}(Q^{\displaystyle hat}{c}{-}T. (*hat {beta }}-c)}$

제약 조건이 있는 추정기에 대한 이 식은 행렬^T XX가 반전 가능한 한 유효합니다.이 기사의 첫머리부터 이 매트릭스가 완전 순위라고 가정했으며, 순위 조건이 실패하면 β를 식별할 수 없다는 점에 주목했다.그러나 제한 A를 추가하면 β를 식별할 수 있으며, 이 경우 추정기의 공식을 찾고자 한다.추정치는 다음과 같습니다.

$displaystyle\hat}^{c}=R(R^{T}XR)^{-1}R^{\displaystyleT}X^{T}y+{\Big (}I_{p}-R(R^{T}XR)^{-1}R^{T}X{\Big}X(Q^{T}Q)^{-1}c,}$

여기서 R은 행렬 [Q R]이 비균형이고, RQ^T = 0인 p×(p - q) 행렬이다.이러한 행렬은 항상 발견될 수 있지만, 일반적으로 유일하지는 않습니다.XX가 반전 가능한 경우 두 ^[33]번째^T 공식은 첫 번째 공식과 일치합니다.

샘플 플플 플플 。

최소 제곱 추정치는 선형 회귀 모형 모수 β의 점 추정치입니다.그러나 일반적으로 이러한 추정치가 모수의 실제 값에 얼마나 가까운지도 알고 싶습니다.즉, 구간 추정치를 구성하려고 합니다.

우리는 오류 용어 εi의 유통에 대해 어떤 가정을 만들지 않은, 그것은 estimators의 분포를 추론하도록 β ^{\displaystyle{\hat{\beta}}}과σ ^ 2{\displaystyle{\hat{\sigma}}^{2}}. 그럼에도 불구하고, 우리는 s로 그들의 점근 속성을 유도하기 위해 그 중심 극한 정리 적용할 리가 만무하다ample size n은 무한대로 됩니다.표본 크기는 반드시 유한하지만, 일반적으로 n이 "충분히 크다"고 가정하여 OLS 추정기의 실제 분포가 점근 한계에 가깝다고 가정합니다.

모델 가정 하에서 β에 대한 최소 제곱 추정치는 일관적이며(즉, β$^\$hat$\beta })$ 점근 ^[proof]정규 분포를 나타낸다$$.

$displaystyle({\hat {beta}-\beta})\{\rightarrow}{d}}{n}}{n}{n}{n}}{n}}{bigma}}{bigma}{bigmathcgma}{bigmathc}}}}$

$여기$서 Q ${\displaystyle x_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {}^{}}$ ${\displaystyle T^{}{}^{}}$. { $displaystyle Q$_ { $xx$ } =$X^$ { $T }$$X$ 입니다.$}$

(Intervals)

$이$ 점근 분포를 사용하여 $β$의 j번째$$성분에 대한 대략적인 양면 신뢰 구간을 다음과 같이 구성할 수 있다$.$

$]{${{sqrt ${\sigma$}^{$2}\left[Q_{x}^{-1}\right]_{jj}}\{bigg]}}$ 1$$ - α 신뢰수준에서

여기서 q는 표준 정규 분포의 분위수 함수를 나타내고 [·]_jj는 행렬의 j번째 대각 원소입니다.

마찬가지로, θ에² 대한 최소 제곱 추정치도 일관되고 점근적으로 정규 분포를 따릅니다(만약_i θ의 네 번째 모멘트가 존재한다면).

${\displaystyle({\sigma }^2}-\sigma ^{2}\xright {d}\left(0,\;\operatorname {E}\left[\varepsilon _{i}^4}\right]-sigma ^4}\오른쪽.}$

이러한 점근 분포는 예측, 가설 검정, 다른 추정기 구성 등에 사용할 수 있습니다.예시로 예측의 문제를 생각해 보세요.${\displaystyle {x\mathrm{}}_{}}$ 0$(\$이 회귀 분포 영역 내의 어떤 점이라고 $가정$하면 그 시점에서 어떤 응답 변수가 존재했을지 알고 싶습니다.평균 $응답$은 y ${\displaystyle {0\mathrm{}}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {x\mathrm{}}_{}^{}}$ ${\displaystyle {\mathrm{}}_{}^{}}$ ${\displaystyle T_{}^{}}$β {\$displaystyle$$$y_{0$} = x_{0}^{\mathrm${T$}\display$ $\}$입니다. 반면 예측 ${\displaystyle {응답}_{}}$은${\displaystyle {\stackrel{}{}}_{}}$y ^ ${\displaystyle {}_{}^{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {x\mathrm{}}_{}^{}}$ ${\displaystyle 0_{}^{}\stackrel{}{}}$ T${\displaystyle \stackrel{}{}}$β$$^ {$displaystyle$ {$y}_{$0} =$x 0$ ^{0}^{\$mathrm {T}$} } } } } } $}$ } $}$} $beta$ beta beta beta beta beta beta beta beta beta 。β$^$ { $displaystyle$} $\{$ $hat }$의 그것에서 벗어났습니다.

$arrow {}^{-1}\right}\hatsty}\styleft(오른쪽)\styleft)\{{{\hat}\right}\styleft}\sty}\right$

이를 통해 평균 $응답{\displaystyle {}_{}}$ $(\$에 대한 신뢰구간을 구성할 수 있습니다.

$]{$1 - α 신뢰수준에서 {{$sqrt {\sigma$}^{2$}x_{0}^{\mathrm {T}}Q_$${x}{-1}x_{0}}\right}.$

이 섹션은 확장해야 합니다.추가하시면 됩니다. (2017년 2월)

특히 두 가지 가설 검정이 널리 사용됩니다.첫째, 추정된 회귀 방정식이 단순히 반응 변수의 모든 값이 표본 평균과 동일하다고 예측하는 것보다 나은지 여부를 확인하려고 합니다(그렇지 않으면 설명력이 없다고 함).추정된 회귀 분석의 설명 값이 없다는 귀무 가설을 F-검정을 사용하여 검정합니다.계산된 F-값이 유의성의 사전 선택 수준에 대한 임계 값을 초과할 정도로 충분히 큰 것으로 확인되면 귀무 가설이 기각되고 회귀에 설명력이 있다는 대립 가설이 받아들여집니다.그렇지 않으면 설명력이 없다는 귀무 가설이 받아들여집니다.

둘째, 관심 있는 각 설명 변수에 대해 추정된 계수가 0과 유의하게 다른지, 즉 이 특정 설명 변수가 실제로 반응 변수를 예측하는 데 설명력이 있는지 여부를 알고자 한다.여기서 귀무 가설은 참 계수가 0이라는 것입니다.이 가설은 계수의 t-통계량을 표준 오차에 대한 계수 추정치의 비율로 계산하여 검정합니다.t-통계량이 미리 결정된 값보다 크면 귀무 가설이 기각되고 변수는 계수가 0과 유의하게 다른 설명력을 갖는 것으로 확인됩니다.그렇지 않으면 참 계수의 0 값에 대한 귀무 가설이 받아들여집니다.

또한 Chow 검정은 두 개의 하위 표본이 동일한 기본 참 계수 값을 가지는지 여부를 검정하는 데 사용됩니다.각 부분 집합과 결합된 데이터 집합의 회귀 제곱 잔차의 합계는 F-통계량을 계산하여 비교됩니다. F-통계량이 임계값을 초과하면 두 부분 집합 사이에 차이가 없다는 귀무 가설이 기각되고, 그렇지 않으면 합격됩니다.

실제 데이터를 사용한 예

다음 데이터 세트는 30~39세 미국 여성의 평균 키와 체중을 나타낸다(출처:The World Almanac and Book of Facts, 1975).

이(m)	1.47	1.50	1.52	1.55	1.57	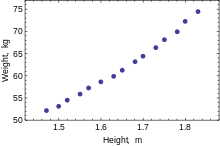데이터의 산점도. 관계가 약간 곡선이지만 선형에 가깝습니다.
량(kg)	52.21	53.12	54.48	55.84	57.20
이(m)	1.60	1.63	1.65	1.68	1.70
량(kg)	58.57	59.93	61.29	63.11	64.47
이(m)	1.73	1.75	1.78	1.80	1.83
량(kg)	66.28	68.10	69.92	72.19	74.46

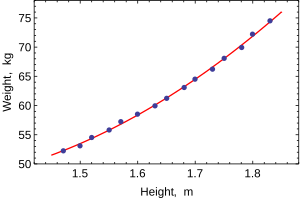
종속 변수가 하나만 모형화되는 경우 산점도는 종속 변수와 회귀 변수 간의 관계 형태와 강도를 나타냅니다.또한 특이치, 이질적 반응성 및 적합 회귀 모형의 해석을 복잡하게 만들 수 있는 데이터의 다른 측면도 나타낼 수 있습니다.산점도는 관계가 강하며 2차 함수로 근사할 수 있음을 나타냅니다.OLS는 회귀기를 도입하여 비선형 관계를 처리할 수 있습니다.HEIGHT그러면 회귀 모델이 다중 선형 모델이 됩니다².

${{i}=\displaystyle_{1}+\display_{2}h_{i}+\display_{3}h_{i}+\varepsilon_{i}.}$

가장 일반적인 통계 패키지의 출력은 다음과 같습니다.

★★★	제곱 least
Dependent 변수)	중중
결과	15
'''	치		자 t	p
$displaystyle _{1}$	128.8128	16.3083	7.8986	0.0000
$displaystyle_{2}}$	–186.1620	19.8332	7.2183	0.0000
$displaystyle_{3}}$	61.9603	6.0084	10.3122	0.0000
R2	0.9989	.E.		0.2516
조정된2 R	0.9987	모델합계		692.61
우도	1.0890	잔존합계		0.7595
빈왓왓왓왓왓통통통	2.1013	★★★★★★★★★★★★★★★★★★★		693.37
	0.2548	계 f		5471.2
	0.3964	(p-set(F-stat)		0.0000

표에서:

• 값 열은 모수의_j 최소 제곱 추정치를 제공합니다β
• 표준 오류 열에는 각 계수 추정치의 표준 오류가 $표시$됩니다. ${\displaystyle {\stackrel{}{^}}_{}}$ ${\displaystyle {j^{\mathrm{}}}^{}}$ ${\displaystyle {}^{}}$ ( ${\displaystyle {{\stackrel{}{^}}^{}}^{}}$ ${\displaystyle {{}^{}{}_{}}^{}}$ ${\displaystyle {{{}_{}^{}}_{}}^{}}$[ ${\displaystyle {{Q_{}^{}}_{}}^{}}$ ${\displaystyle {{{\mathrm{x}}_{}^{}}_{}}^{}}$ - ${\displaystyle {{}_{{}_{}^{}}}^{\frac{\mathrm{j}}{}}}$ ) 1$2$ \ displaystyle { \ $hat }$_ {$j } =$ \ left \ $hat$ { $right$} { Q _$x$}^{ } { right $}$ { $j ^$2$fr1 }$
• t-통계량 및 p-값 열은 계수 중 0이 될 수 있는 계수가 있는지 여부를 검정합니다.t-module은 $단순히$ t ${\displaystyle =}$ ${\displaystyle \beta {\stackrel{}{}}_{}{\stackrel{}{}}_{}}$^${\displaystyle {}_{}}$j /${\displaystyle {\stackrel{}{}}_{}}$^ ${\displaystyle j_{}}${ $displaystyle$ t =$snewhat {j}/{\hat$ {$newhat }}_{j$로 계산됩니다.오류 follow가 정규 분포를 따르는 경우 t는 Student-t 분포를 따릅니다.약한 조건에서는 t가 점근 정규 분포를 따릅니다.t 값이 크면 귀무 가설을 기각할 수 있고 해당 계수가 0이 아님을 나타냅니다.두 번째 열인 p-값은 가설 검정 결과를 유의 수준으로 나타냅니다.일반적으로 0.05보다 작은 p-값은 모집단 계수가 0이 아니라는 증거로 사용됩니다.
• R-제곱은 회귀의 적합도를 나타내는 결정 계수입니다.이 통계량은 적합치가 완벽하면 1이 되고 회귀군 X에 설명력이 없으면 0이 됩니다.이는 모집단 R-제곱에 대한 편향된 추정치이며, 관련이 없더라도 회귀 분석기를 더해도 절대 감소하지 않습니다.
• $조정$된 R-제곱은 $2$의 $약간{\displaystyle {}^{}}$ 수정된 버전으로, 회귀의 설명 파워를 추가하지 않는 과도한 수의 회귀에 대해 불이익을 주도록 설계되었습니다$.$이 통계는 항상 ${\displaystyle {R\mathrm{}}^{}}2$보다 작으며({$displaystyle$ R$^{2$ 새로운 회귀기가 추가되면 감소할 수 있으며, 적합성이 떨어지는 모델의 경우 음수일 수도 있습니다.

$displaystyle {R}^2}=1-{\frac {n-1}{n-p}(1-R^{2})}$

• 로그 우도는 오차가 정규 분포를 따른다는 가정 하에 계산됩니다.이 가정이 매우 합리적이지 않더라도, 이 통계량은 여전히 LR 테스트를 수행할 때 사용될 수 있습니다.
• 더빈-왓슨 통계량은 잔차 사이에 직렬 상관 관계가 있다는 증거가 있는지 여부를 검정합니다.경험적으로 2보다 작은 값은 양의 상관 관계가 있다는 증거가 됩니다.
• Akaike 정보 기준과 Schwarz 기준은 둘 다 모델 선정에 사용된다.일반적으로 두 가지 대체 모형을 비교할 때 이러한 기준 중 하나의 값이 작을수록 ^[34]더 나은 모형을 나타냅니다.
• 회귀의 표준 오차는 오차항의 표준 오차인 ,의 추정치입니다.
• 총 제곱합, 모형 제곱합 및 잔차 제곱합은 표본의 초기 변동 중 어느 정도가 회귀 분석을 통해 설명되었는지를 나타냅니다.
• F-통계량은 절편을 제외한 모든 계수가 0이라는 가설을 검정하려고 합니다.이 통계량은 귀무 가설과 정규성 가정 하에서 F(p–1,n–p) 분포를 가지며 p-값은 가설이 실제로 참일 확률을 나타냅니다.오류가 정규적이지 않은 경우 이 통계량은 무효가 되며 Wald 테스트나 LR 테스트와 같은 다른 테스트를 사용해야 합니다.

일반 최소 제곱 분석에는 종종 모형의 가정된 형식에서 데이터의 이탈을 탐지하도록 설계된 진단 그림의 사용이 포함됩니다.플롯은 과 같습니다.

• 이치이러한 변수 사이의 비선형 관계는 조건부 평균 함수의 선형성이 유지되지 않을 수 있음을 나타냅니다.설명 변수의 여러 수준에 대한 잔차의 변동 수준이 다르다는 것은 이교차성이 있을 수 있음을 나타냅니다.
• 모형에 없는 설명 변수에 대한 잔차입니다.나머지의 이러한 변수 어떤 관련이라도 있는 건가 모델에 포함시키기 위한 이러한 변수를 고려했을 때 제안할 것이다.잔차와 이러한 변수의 관계는 모형에 포함하기 위해 이러한 변수를 고려하는 것이 좋습니다.
• 적합치에 대한 잔차, $y{\displaystyle \hat{}}${\$style {y$
• 이전 잔차에 대한 잔차.이 그림은 잔차에서 일련 상관 관계를 식별할 수 있습니다.

회귀 모델을 사용하여 통계적 추론을 수행할 때 중요한 고려사항은 데이터가 어떻게 샘플링되었는가이다.이 예에서 데이터는 개별 여성에 대한 측정값이 아니라 평균값입니다.모델의 핏감은 매우 좋지만, 키만으로 여성의 체중을 정확하게 예측할 수 있는 것은 아닙니다.

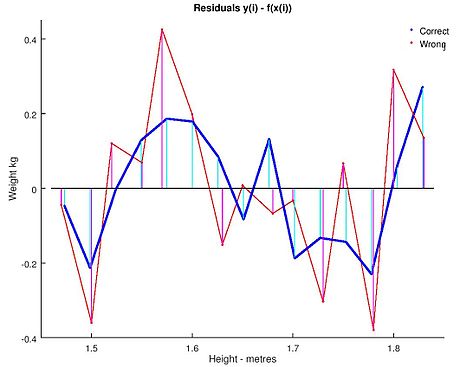
반올림 감도

또한 이 예제는 이러한 계산에 의해 결정되는 계수가 데이터 준비 방법에 민감하다는 것을 보여줍니다.높이는 원래 가장 가까운 인치로 반올림되었고 가장 가까운 센티미터로 변환되고 반올림되었다.변환 계수가 1인치에서 2.54cm이므로 정확한 변환은 아닙니다.원래 인치는 라운드(x/0.0254)로 복구한 후 반올림하지 않고 미터법으로 다시 변환할 수 있습니다.이렇게 하면 다음과 같은 결과가 됩니다.

	계속	높이	높이2
반올림을 통해 미터법으로 변환됩니다.	128.8128	−143.162	61.96033
반올림 없이 미터법으로 변환됩니다.	119.0205	−131.5076	58.5046

이 방정식들 중 하나를 사용하여 5인치 6인치(1.6764m) 여성의 체중을 예측하면 비슷한 값을 얻을 수 있다: 반올림 시 62.94kg 대 반올림 시 62.98kg.따라서 데이터의 작은 변동은 계수에 실질적인 영향을 미치지만 방정식의 결과에는 작은 영향을 미칩니다.

이것은 데이터 범위의 중간에서 무해해해 보일 수 있지만, 극단적으로 중요하거나 적합 모델을 사용하여 데이터 범위를 벗어나는 경우(삭제)에 유의할 수 있습니다.

이것은 일반적인 에러를 나타내고 있습니다.이 예에서는 OLS를 남용하고 있습니다.이 예에서는 본질적으로 독립 변수(이 경우 높이)의 에러가 제로이거나 최소한 무시할 수 있어야 합니다.가장 가까운 인치까지의 초기 반올림 및 실제 측정 오차는 유한하고 무시할 수 없는 오차를 구성합니다.결과적으로 적합 모수는 추정된 최선의 추정치가 아닙니다.완전히 가짜는 아니지만 추정 오류는 x 및 y 오류의 상대적 크기에 따라 달라집니다.

실제 데이터가 적은 또 다른 예

문제문

극 기저 좌표의 두 물체 궤도의 방정식을 구하기 위해 최소 제곱 메커니즘을 사용할 수 있습니다.${\displaystyle \mathrm{일반적}}$으로 사용되는 방정식은 ${\displaystyle \frac{r}{}}$( ${\displaystyle )}$ ) ${\displaystyle =}$ ${\displaystyle \frac{p\mathrm{}}{}}$1 - e ${\displaystyle \frac{\cos }{}}$ ${\displaystyle \frac{（}{}}$ ${\displaystyle \frac{)}{}}$ {\ $）$ { $displaystyle$ r ( \$theta$ ) =$frac${$p$} { 1 -$$ \ $cos$( \ $theta )}$ 입니다${\displaystyle .\mathrm{여기}}$서 r ( ${\displaystyle )}$) { $displaystyle r$( \ theta$$) }는$$ 물체의 반경입니다.방정식에서는 p$\displaystyle$p와$$ $\displaystyle$e를$$ $사용$하여 궤도의 경로를 결정합니다.이하의 데이터를 측정했습니다.

$§$ $\displaystyle$ \theta$$}$$ ($도$ 단위)	43	45	52	93	108	116
${\displaystyle r(\theta)}$	4.7126	4.5542	4.0419	2.2187	1.8910	1.7599

주어진 데이터에 대한$e$와$p$의 $최소{\displaystyle }$ 제곱 근사치를 구해야 합니다$.$

솔루션

먼저 e와 p를 선형으로 표현해야 합니다.$r{\displaystyle }$ ( ${\displaystyle (}$) {${\displaystyle }$${\displaystyle \frac{\mathrm{displaystyle}}{}}$ r ( \$theta$) ${\displaystyle \frac{}{}}$ ${\displaystyle 1\frac{p}{}}$ - ${\displaystyle e}$ ${\displaystyle \frac{\cos }{}}$ ${\displaystyle }$ (${\displaystyle \frac{}{})}$) （ ） = $displaystyle${ { 1$$} { $r$( \ $theta$ ) = sc $frac${ $1$} { $p$} - { $p$} - { p } $cos$( \$ta )$ $）$ ${\displaystyle \mathrm{1<img\; alt="r(\backslash theta)"\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/53df06e661affb927fb93a95195225e3455cf572"\; style="vertical-align:\; -0.838ex;\; width:3.948ex;\; height:2.843ex;">}}$ to 1 。

$=$$T{\displaystyle }$$}b$$$x$${\$displaystyle$$x}$는 $1p,$$y{\displaystyle }$ {\$displaystyle$ y$}$는 ${\displaystyle \frac{e}{}}$ p$${\$displaystyle$${$$e}$ {$p}$이며$,$ $A{\displaystyle }$ {\$displaystyle$A}는$1p$의 $계수$인 첫 번째 열과 두 번째 열 $coi$로 구성됩니다.e$$(\$displaystyle {e}$ {$p}}$ 및$$$b{\displaystyle }$(\$$b})의 cient는 ${\displaystyle \frac{각}{}}$ 1r$($)(\$displaystyle {1}r(\theta)})$에 대한 값이며, 따라서 - 0. 1 - 0.1..05.17.05..17..17.03.17.01.03.17.17.01.01.01.03.17.17.17.01.01.05.17.05.17.17.01.01.0$ix}1&-0.731354\1&-0.707107\1&0.615661\1&0.052336\1.309017\1&0.438371\end{bmatrix}}$ 및 $b{\displaystyle =\begin{array}{c}\mathrm{}\\ \mathrm{[}\\ 0\end{array}}$.${\displaystyle \begin{array}{}21958\\ \mathrm{.}2471\\ \mathrm{]}\\ \mathrm{0<img\; alt="\{\backslash displaystyle\; A=\{\backslash begin\{bmatrix\}1\&-0.731354\backslash \backslash 1\&-0.707107\backslash \backslash 1\&-0.615661\backslash \backslash 1\&\backslash \; 0.052336\backslash \backslash 1\&0.309017\backslash \backslash 1\&0.438371\backslash end\{bmatrix\}\}\}"\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/34fc8d166bafb54cf16ab4f47496d630e145b6cd"\; style="vertical-align:\; -9.005ex;\; width:22.771ex;\; height:19.176ex;">}\end{array}}$.${\displaystyle \begin{array}{}56181\end{array}}$.$}$

풀면 (${\displaystyle \genfrac{}{}{0ex}{}{x}{}}$y )${\displaystyle =}$ (${\displaystyle \genfrac{}{}{0ex}{}{\mathrm{}}{}0}$ . ${\displaystyle \genfrac{}{}{0ex}{}{43478}{}}$ 0.${\displaystyle \genfrac{}{}{0ex}{}{30435}{}}$ ${\displaystyle )}${ $displaystyle${$binom$ { x } { y } =$binom { 0$ . $43478$} { 0.$30435$}

$따라서{\displaystyle }$ p ${\displaystyle =}$ ${\displaystyle 1\frac{\mathrm{}}{}}$ ${\displaystyle \frac{x}{}}$ $=$ p$=squalfrac {1}{x$}}=$2).$$3000}$ $및$ e ${\displaystyle =}$ ${\displaystyle p}$ ${\displaystyle \cdot }$ ${\displaystyle \mathrm{1024}}$ y ${\displaystyle =0.70001}$({$displaystyle$ e$=p\cdot$ y$=0.70001)$

「 」를 참조해 주세요.

• 베이지안 최소 제곱
• 파마-맥베스 회귀
• 비선형 최소 제곱
• 선형 최소 제곱에 대한 숫자 방법
• 비선형 시스템 식별

레퍼런스

추가 정보

• Dougherty, Christopher (2002). Introduction to Econometrics (2nd ed.). New York: Oxford University Press. pp. 48–113. ISBN 0-19-877643-8.
• Gujarati, Damodar N.; Porter, Dawn C. (2009). Basic Econometics (Fifth ed.). Boston: McGraw-Hill Irwin. pp. 55–96. ISBN 978-0-07-337577-9.
• Heij, Christiaan; Boer, Paul; Franses, Philip H.; Kloek, Teun; van Dijk, Herman K. (2004). Econometric Methods with Applications in Business and Economics (1st ed.). Oxford: Oxford University Press. pp. 76–115. ISBN 978-0-19-926801-6.
• Hill, R. Carter; Griffiths, William E.; Lim, Guay C. (2008). Principles of Econometrics (3rd ed.). Hoboken, NJ: John Wiley & Sons. pp. 8–47. ISBN 978-0-471-72360-8.
• Wooldridge, Jeffrey (2008). "The Simple Regression Model". Introductory Econometrics: A Modern Approach (4th ed.). Mason, OH: Cengage Learning. pp. 22–67. ISBN 978-0-324-58162-1.