코헨의 카파

Cohen's kappa coefficient(κ, 소문자 그리스어 kappa)는 정성적(범주적) 항목에 대한 평가자 간 신뢰도(및 평가자 내 신뢰도)를 측정하는 데 사용되는 통계량입니다. 일반적으로 κ가 우연히 합의가 발생할 가능성을 고려하기 때문에 단순 퍼센트 합의 계산보다 더 강력한 조치로 여겨집니다. 일치 지수 해석의 어려움으로 코헨의 카파를 둘러싼 논란이 있습니다. 일부 연구자들은 항목 간의 불일치를 평가하는 것이 개념적으로 더 간단하다고 제안했습니다.^[2]

역사

카파 유사 통계에 대한 최초의 언급은 1892년에 Galton에 기인합니다.^[3][4]

새로운 기법으로 카파를 소개하는 중요한 논문은 1960년 제이콥 코헨(Jacob Cohen)이 학술지 교육 및 심리 측정(Educational and Psychological Measurement)에 발표했습니다.^[5]

정의.

Cohen의 kappa는 N개의 항목을 각각 C개의 상호 배타적 범주로 분류하는 두 평가자 간의 일치를 측정합니다. κ${\textstyle$ \kappa}의 정의는

${\displaystyle \kappa \equiv {\frac {p_{o}-p_{e}}{1-p_{e}}}=1-{\frac {1-p_{o}}{1-p_{e}}},}$

여기서 p는_o 평가자 간의 상대적인 일치도이고 p는_e 관측된 데이터를 사용하여 각 범주를 무작위로 보는 각 관측자의 확률을 계산하는 가설적인 우연 일치 확률입니다. 평가자들이 완전히 일치하는 경우 κ = 1 ${\textstyle$ \kappa = 1}입니다. 평가자들 사이에 우연히 예상되는 것(p로 표시된 것) 이외에 일치하는 것이 없으면 κ = 0 {\textstyle \kappa = 0}입니다. 통계치가 음수일 가능성이 있으며,^[6] 이는 두 평정자의 평정 간에 아무런 관계가 없는 경우에 우연히 발생할 수도 있고, 평정자가 다른 평정을 부여하는 실제 성향을 반영할 수도 있습니다.

범주 k에 대해 N개의 관측치가 범주화하고 ${\displaystyle {n개}_{}}$의 ${\displaystyle {\mathrm{ki}}_{}}$ ${\$개의 범주 k를 예측한 횟수:

${\displaystyle p_{e}={\frac {1}{N^{2}}}\sum _{k}n_{k1}n_{k2}}$

이는 다음과 같은 구성에서 파생됩니다.

${\displaystyle p_{e}=\sum_{k}{\widehat {p_{k12}}{\text{ind}를(를) 재정의했습니다.}}{=}}\sum _{k}{\widehat {p_{k1}}}{\widehat {p_{k2}}}=\sum _{k}{\frac {n_{k1}}{N}}{\frac {n_{k2}}{N}}={\frac {1}{N^{2}}}\sum _{k}n_{k1}n_{k2}}$

$여기$서 ${\displaystyle \stackrel{}{{pk}_{}}}$ $^$ {\$displaystyle${\$widehat {p_{k12}}}$는 Rater 1과 Rater 2가 동일한 항목을 k로 분류할 것이라는 추정 확률이고, ${\displaystyle \stackrel{}{{pk}_{}}}$ $^$ {\$displaystyle${\$widehat$ {$p_{k1}}$는 Rater 1이 항목을 k로 분류할 것이라는 추정 확률입니다$$(그리고 Rater 2의 경우도 마찬가지입니다). $\stackrel{}{{\mathrm{관계}}_{}}$ $p$ $\stackrel{}{k_{}}$ = ∑$$k p k$$1 ^ p k^ 2 ^ {\textstyle {\widehat {p_{k}} =\sum_{k} {\widehat {p_{k1}} {\widehat {p_{k2}}는 두 평가자의 등급이 독립적이라는 가정을 사용한 것입니다. The term ${\displaystyle {\widehat {p_{k1}}}}$ is estimated by using the number of items classified as k by rater 1 (${\displaystyle n_{k1}}$) divided by the total items to classify (${\displaystyle N}$): ${\displaystyle {\widehat {p_{k1}}}={n_{k1} \over$$N}}($후자 2의 경우에도 마찬가지).

이진분류혼란행렬

이진 분류를 평가하기 위한 기계 학습 및 통계에 사용되는 전통적인 2 × 2 혼동 행렬에서 코헨의 카파 공식은 다음과 같이 쓸 수 있습니다.^[7]

${\displaystyle \kappa ={\frac {2\times (TP\times TN-FN\times FP)}{(TP+FP)\times (FP+TN)+(TP+)FN)\times (FN+TN)}}}$

여기서 TP는 참 양성, FP는 거짓 양성, TN은 참 음성, FN은 거짓 음성입니다. 이 경우 코헨의 카파는 기상학에서 알려진 하이드케 기술 점수와 맞먹습니다.^[8] 이 방법은 1888년 마이릭 해스켈 둘리틀에 의해 처음으로 도입되었습니다.^[9]

예

단순예시

보조금을 신청하는 50명의 그룹과 관련된 데이터를 분석했다고 가정해 보겠습니다. 각 보조금 제안서는 두 명의 독자가 읽었고 각 독자는 제안서에 대해 "예" 또는 "아니오"라고 답했습니다. 불일치 횟수 데이터가 다음과 같다고 가정합니다. 여기서 A와 B는 판독기, 행렬(a와 d)의 주 대각선 데이터는 일치 횟수를 계산하고 대각선 이외의 데이터(b와 c)는 불일치 횟수를 계산합니다.

B A	네.	아니요.
네.	a	b
아니요.	c	d

예.

B A	네.	아니요.
네.	20	5
아니요.	10	15

관측된 비례적 일치는 다음과 같습니다.

${\displaystyle p_{o}={\frac {a+d}{a+b+c+d}}={\frac {20+15}{50}}=0.7}$

p_e(무작위 일치 확률)를 계산하기 위해 다음 사항에 유의합니다.

• 독자 A씨는 지원자 25명에게 '예', 지원자 25명에게 '아니오'라고 답했습니다. 그래서 독자 A는 50%를 "예"라고 답했습니다.
• B독자는 지원자 30명에게 '예', 20명에게 '아니오'라고 답했습니다. 그래서 독자 B는 60%가 "예"라고 답했습니다.

따라서 둘 다 임의로 예라고 대답할 것으로 예상되는 확률은 다음과 같습니다.

${\displaystyle p_{\text}Yes}}={\frac {a+b}{a+b+c+d}}\cdot {\frac {a+c}{a+b+c+d}}=0.5\times 0.6=0.3}$

마찬가지로:

${\displaystyle p_{\text{No}}={\frac {c+d}{a+b+c+d}}\cdot {\frac {b+d}{a+b+c+d}}=0.5\times 0.4=0.2}$

전체 랜덤 일치 확률은 예 또는 아니오에 대해 일치할 확률입니다. 즉, 다음과 같습니다.

${\displaystyle p_{e}=p_{\text{Yes}}+p_{\text{No}}=0.3+0.2=0.5}$

이제 코헨의 카파 공식을 적용하면 다음과 같습니다.

${\displaystyle \kappa ={\frac {p_{o}-p_{e}}{1-p_{e}}}={\frac {0.7-0.5}{1-0.5}}=0.4}$

같은 백분율이지만 다른 숫자

Cohen's Kappa의 문제로 간주되는 경우는 두 개의 평가자 쌍에 대해 계산된 Kappa와 각 쌍의 두 평가자가 동일한 백분율 일치를 갖지만 한 쌍은 각 클래스에서 비슷한 수의 등급을 제공하고 다른 쌍은 각 클래스에서 매우 다른 수의 등급을 제공하는 경우에 발생합니다.^[10] (아래의 경우 B공지는 첫 번째 경우에 70개의 예와 30개의 노가 있지만 두 번째 경우에는 그 숫자가 반대입니다.) 예를 들어, 다음의 두 경우에는 A와 B 사이에 각 클래스의 합의에 있어서 동등한 합의가 존재하기 때문에 (두 경우 모두 100점 만점에 60점) Cohen의 Kappa의 상대적인 값이 이를 반영할 것으로 기대합니다. 그러나 각각의 코헨의 카파를 계산하면 다음과 같습니다.

B A	네.	아니요.
네.	45	15
아니요.	25	15

${\displaystyle \kappa ={\frac {0.60-0.54}{1-0.54}}=0.1304}$

B A	네.	아니요.
네.	25	35
아니요.	5	35

${\displaystyle \kappa ={\frac {0.60-0.46}{1-0.46}}=0.2593}$

첫 번째 경우에 비해 두 번째 경우에서 A와 B 사이에 더 큰 유사성을 보인다는 것을 발견했습니다. 백분율 일치율은 동일하지만 '우연하게' 발생할 백분율 일치율은 첫 번째 경우(0.46에 비해 0.54)가 상당히 높기 때문입니다.

특성.

가설 검정 및 신뢰 구간

카파에 대한 P-값은 거의 보고되지 않는데, 아마도 상대적으로 낮은 카파 값도 0과 크게 다를 수 있지만 조사자를 만족시키기에 충분한 크기가 아니기 때문일 것입니다.^{[11]: 66} 여전히 표준 오차는 설명되어^[12] 있으며 다양한 컴퓨터 프로그램에 의해 계산됩니다.^[13]

무한히 많은 항목을 확인한 경우 예상되는 카파 값에 대해 다음 공식을 사용하여 카파에 대한 신뢰 구간을 구성할 수 있습니다.^[1]

${\displaystyle CI:\kappa \pm Z_{1-\alpha /2}SE_{\kappa}}$

Where ${\displaystyle Z_{1-\alpha /2}=1.960}$ is the standard normal percentile when ${\displaystyle \alpha =5\%}$, and ${\displaystyle SE_{\kappa }={\sqrt {{p_{o}(1-p_{o})} \over {N(1-p_{e})^{2}}}}}$

이 값은 데이터에서_e p가 추정된다는 사실을 무시하고 점근 정규성을 사용하는 동안_o p를 이항 분포의 추정 확률로 처리함으로써 계산됩니다(즉, 항목 수가 많고_o p가 0 또는 1에 가깝지 않다고 가정함). $κ$ {\displaystyle SE_${\$kappa}}(및 일반적인 CI)는 부트스트랩 방법을 사용하여 추정할 수도 있습니다.

해석크기

통계적 유의성이 유용한 가이드가 아닌 경우 적절한 일치를 반영하는 카파의 크기는 얼마입니까? 지침은 도움이 되겠지만 일치 이외의 요인이 크기에 영향을 미칠 수 있으므로 주어진 크기를 해석하는 데 문제가 있습니다. Sim과 Wright가 언급한 바와 같이, 두 가지 중요한 요인은 유병률(코드가 동일한지 또는 확률이 다양한지)과 편향(두 관측자의 한계 확률이 유사한지 또는 서로 다름인지)입니다. 다른 것들이 같다면, 카파는 코드가 등용 가능할 때 더 높습니다. 반면, 카파스는 두 관측자에 의해 코드가 비대칭적으로 분포될 때 더 높습니다. 확률 변동과 대조적으로, 편향의 효과는 카파가 클 때보다 작을 때 더 큽니다.^{[14]: 261–262}

또 다른 요인은 코드 수입니다. 코드 수가 증가함에 따라 kappas는 더 높아집니다. 시뮬레이션 연구를 기반으로 Bakeman과 동료들은 오류가 발생할 수 있는 관찰자의 경우 코드가 적을 때 카파 값이 더 낮다는 결론을 내렸습니다. 그리고, 유병률에 관한 심 & 라이트의 진술과 일치하여, 카파는 코드가 대략적으로 적합할 때 더 높았습니다. 따라서 Bakeman et al.은 "카파의 어떤 값도 보편적으로 허용되는 것으로 간주될 수 없다"^{[15]: 357} 고 결론지었습니다. 또한 사용자가 코드 수, 확률 및 관찰자 정확도를 지정하는 카파 값을 계산할 수 있는 컴퓨터 프로그램을 제공합니다. 예를 들어, 85% 정확한 등확률 코드와 관측자가 주어진 경우, 코드 수가 2, 3, 5 및 10일 때 카파의 값은 각각 0.49, 0.60, 0.66 및 0.69입니다.

그럼에도 불구하고 규모 지침이 문헌에 등장했습니다. 아마도 첫 번째는 란디스와 코흐(Landis and Koch)^[16]로서 값 <0은 일치하지 않음을 나타내고 0–0.20은 약간, 0.21–0.40은 공정, 0.41–0.60은 중간, 0.61–0.80은 상당, 0.81–1은 거의 완벽한 일치를 나타내는 것으로 특성화했습니다. 그러나 이 일련의 지침은 보편적으로 받아들여지는 것은 아닙니다. 란디스와 코흐는 대신 개인 의견에 근거하여 이를 뒷받침하는 증거를 제공하지 않았습니다. 이러한 지침은 도움이 되기보다 더 해로울 수 있다는 점에 주목했습니다.^[17] Fleiss의 동일하게 임의적인 지침은^{[18]: 218} 0.75 이상의 카파를 우수한 것으로, 0.40~0.75 이상을 공정한 것으로, 0.40 미만을 불량한 것으로 특징짓습니다.

카파 최대치

Kappa는 두 관측자가 코드를 동일하게 분포하는 경우, 즉 해당 행과 열의 합이 동일한 경우에만 이론적 최대값을 1로 가정합니다. 이보다 작은 것은 완벽한 합의보다 적습니다. 그러나 주어진 동일하지 않은 분포에서 카파가 달성할 수 있는 최대값은 실제로 얻은 카파의 값을 해석하는 데 도움이 됩니다. κ 최대값에 대한 식은 다음과 같습니다.

${\displaystyle \kappa _{\max }={\frac {P_{\max }-P_{\exp }}{1-P_{\exp }}}}$

여기서 $P$ ${\displaystyle \underset{}{\overset{}{exp}}}$ = ∑${\displaystyle \underset{}{\overset{}{}}}$i =${\displaystyle \underset{}{\overset{}{}}}$1 $Pi$ + P + i {\displaystyle P_{\exp} =\sum _{i=1}^{k}P_{i+}P_{+i}}, 일반적으로 P max = ∑ i = 1 kmin (Pi +, P + i ) {\displaystyle P_{\max } =\sum _{i=1}^{k}\min(P_{i+}, P_{+i})},

k = 코드 수, ${\displaystyle {Pi}_{}}$+ ${\displaystyle P_{i+}$는 행 확률, P${\displaystyle {}_{}}$+ ${\displaystyle i_{}}$ ${\displaystyle P_{+i}$는 열 확률입니다.

한계

Kappa는 기준 일치와 관련하여 관측된 일치를 고려하는 지표입니다. 그러나 연구자들은 카파의 기본 합의가 특정 연구 문제와 관련이 있는지 신중하게 고려해야 합니다. 카파의 기준선은 종종 우연으로 인한 합의로 설명되는데, 이는 부분적으로만 옳습니다. Kappa의 기본 합의는 제곱 분할표의 한계 합계에 의해 지정된 양을 고려할 때 무작위 할당으로 인해 예상되는 합의입니다. 따라서 관측된 할당이 한계 총계에 의해 제한된 수량 불일치와 관계없이 분명히 무작위인 경우 κ = 0입니다. 그러나 많은 응용 프로그램의 경우 조사자는 제곱 분할표 대각선의 추가 정보에 의해 설명되는 할당 불일치보다 한계 합계의 수량 불일치에 더 관심을 가져야 합니다. 따라서 많은 애플리케이션에서 Kappa의 기준선은 깨우침을 주는 것보다 주의를 산만하게 합니다. 다음 예를 생각해 보십시오.

비교1

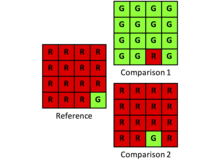
		언급
		G	R
비교	G	1	14
	R	0	1

불일치 비율은 14/16 또는 0.875입니다. 할당이 최적이기 때문에 수량 때문에 의견이 일치하지 않습니다. κ은 0.01입니다.

비교2

		언급
		G	R
비교	G	0	1
	R	1	14

불일치 비율은 2/16 또는 0.125입니다. 수량이 동일하기 때문에 할당 때문에 의견이 일치하지 않습니다. Kappa is −0.07.

여기서 수량 및 할당 불일치 보고는 정보를 제공하는 반면 카파는 정보를 숨깁니다. 더 나아가 카파는 비율이기 때문에 계산과 해석에서 몇 가지 어려움을 도입합니다. 카파의 비율은 분모에서 0으로 인해 정의되지 않은 값을 반환할 수 있습니다. 또한 비율은 분자나 분모를 나타내지 않습니다. 연구자들은 수량과 할당의 두 가지 구성 요소에서 불일치를 보고하는 것이 더 유용합니다. 이 두 성분은 단일 요약 통계량보다 범주 간의 관계를 더 명확하게 설명합니다. 예측 정확도가 목표일 때, 연구자들은 카파의 한 비율이 아니라 수량과 할당의 두 성분을 사용하여 예측을 개선하는 방법에 대해 더 쉽게 생각할 수 있습니다.^[2]

일부 연구자들은 관찰된 범주의 빈도를 주어진 것으로 간주하는 κ의 경향에 대해 우려를 표명했는데, 이는 희귀 질병 진단과 같은 상황에서 일치를 측정하는 것을 신뢰할 수 없게 만들 수 있습니다. 이런 상황에서 κ은 희귀 범주에 대한 합의를 과소평가하는 경향이 있습니다. 이러한 이유로 κ은 지나치게 보수적인 합의의 척도로 여겨집니다. 다른^{[22][citation needed]} 사람들은 카파가 우연한 합의를 "고려"한다는 주장에 이의를 제기합니다. 이를 효과적으로 수행하려면 우연이 추후 결정에 어떤 영향을 미치는지에 대한 명시적 모델이 필요합니다. 카파 통계의 소위 확률 조정은 완전히 확실하지는 않지만, 평가자들이 단순히 추측하는 것, 즉 매우 비현실적인 시나리오를 가정합니다. 또한 일부 연구에서는^[23] 카파 통계량이 불균형 데이터에 대해 잘못된 결론으로 이어질 수 있음을 보여주었습니다.

관련통계

스캇 파이

Pi라고 불리는 비슷한 통계는 Scott(1955)에 의해 제안되었습니다. 코헨의 카파와 스콧의 파이는 p가_e 어떻게 계산되는지에 따라 다릅니다.

플라이스카파

Cohen의 kappa는 두 평가자 간의 일치만을 측정합니다. 두 명 이상의 평정자가 있을 때 사용되는 유사한 일치도(Fleiss' kappa)는 Fleiss(1971)를 참조하십시오. 그러나 Fleiss kappa는 코헨의 kappa가 아니라 Scott의 pi 통계학을 다층적으로 일반화한 것입니다. Kappa는 기계 학습에서 성능을 비교하는 데도 사용되지만 Informedness 또는 Yuden's J 통계량으로 알려진 방향성 버전이 지도 학습에 더 적합하다고 주장됩니다.^[24]

가중 카파

가중치가 부여된 카파를 사용하면 불일치의 가중치를^[25] 다르게 부여할 수 있으며 코드를 정렬할 때 특히 유용합니다.^{[11]: 66} 세 가지 행렬, 관측된 점수 행렬, 우연 일치에 기초한 예상 점수 행렬 및 가중치 행렬이 포함됩니다. 대각선(왼쪽 위에서 오른쪽 아래)에 위치한 가중치 행렬 셀은 일치를 나타내므로 0을 포함합니다. 대각선 밖의 셀에는 불일치의 심각성을 나타내는 가중치가 포함되어 있습니다. 흔히 대각선에서 벗어난 셀 1은 가중치가 1이고, 2에서 벗어난 셀 2는 가중치가 부여됩니다.

가중 κ의 방정식은 다음과 같습니다.

${\displaystyle \kappa =1-{\frac {\sum _{i=1}^{k}\sum _{j=1}^{k}w_{ij}x_{ij}}{\sum _{i=1}^{k}\sum _{j=1}^{k}w_{ij}m_{ij}}}}$

여기서 k=코드 수와 ${\displaystyle {\mathrm{wij}}_{}}$ ${\displaystyle w_{ij$${\displaystyle {\mathrm{xij}}_{}}$ ${\displaystyle x_{ij},$ ${\displaystyle {\mathrm{mij}}_{}}$ ${\displaystyle m_{ij}$는 각각 가중치, 관측치 및 예상 $행렬$의 요소입니다. 대각선 셀의 가중치가 0이고 모든 대각선 외 셀의 가중치가 1일 때 이 공식은 위에 주어진 계산과 동일한 값의 카파를 생성합니다.

참고 항목

• Bangdiwala's B
• 학내상관
• 크리펜도르프 알파
• 통계구분

더보기

• Banerjee, M.; Capozzoli, Michelle; McSweeney, Laura; Sinha, Debajyoti (1999). "Beyond Kappa: A Review of Interrater Agreement Measures". The Canadian Journal of Statistics. 27 (1): 3–23. doi:10.2307/3315487. JSTOR 3315487. S2CID 37082712.
• Chicco, D.; Warrens, M.J.; Jurman, G. (2021). "The Matthews correlation coefficient (MCC) is more informative than Cohen's Kappa and Brier score in binary classification assessment". IEEE Access. 9: 78368–81. doi:10.1109/access.2021.3084050. S2CID 235308708.
• Cohen, Jacob (1960). "A coefficient of agreement for nominal scales". Educational and Psychological Measurement. 20 (1): 37–46. doi:10.1177/001316446002000104. hdl:1942/28116. S2CID 15926286.
• Cohen, J. (1968). "Weighted kappa: Nominal scale agreement with provision for scaled disagreement or partial credit". Psychological Bulletin. 70 (4): 213–220. doi:10.1037/h0026256. PMID 19673146.
• Fleiss, J.L.; Cohen, J. (1973). "The equivalence of weighted kappa and the intraclass correlation coefficient as measures of reliability". Educational and Psychological Measurement. 33 (3): 613–9. doi:10.1177/001316447303300309. S2CID 145183399.
• Sim, J.; Wright, C.C. (2005). "The Kappa Statistic in Reliability Studies: Use, Interpretation, and Sample Size Requirements". Physical Therapy. 85 (3): 257–268. doi:10.1093/ptj/85.3.257. PMID 15733050.
• Warrens, J. (2011). "Cohen's kappa is a weighted average". Statistical Methodology. 8 (6): 473–484. doi:10.1016/j.stamet.2011.06.002. hdl:1887/18062.

외부 링크

• Kappa, 그 의미, 문제점 및 몇 가지 대안 (Link is dead 2022-12-16 현재)
• Kappa 통계량: 장단점
• 소프트웨어 구현
  • 카파, 가중치 카파 및 카파 최대용 Windows 프로그램 "ComKappa"(2022-12-16 기준 "액세스 거부(오류 코드 1020)")

참고문헌