요인 실험
Factorial experiment통계학에서 완전 요인 실험은 둘 이상의 요인(각각 이산 가능한 값 또는 수준)으로 구성되고 실험 단위가 이러한 모든 요인에서 이러한 수준의 가능한 모든 조합을 취하는 실험입니다.완전 요인 설계는 완전 교차 설계라고도 할 수 있습니다.이러한 실험을 통해 조사자는 반응 변수에 대한 각 요인의 효과와 반응 변수에 대한 요인 간의 교호작용 효과를 연구할 수 있습니다.
대부분의 요인 실험에서는 각 요인의 수준이 두 개뿐입니다.예를 들어, 두 요인이 각각 두 가지 수준을 갖는 경우 요인 실험에는 총 네 가지 처리 조합이 있으며 일반적으로 2×2 요인 설계라고 합니다.이러한 설계에서는 변수 간의 교호작용이 가장 중요한 경우가 많습니다.이는 주효과와 상호작용이 존재하는 시나리오에도 적용된다.
완전 요인 설계의 조합 수가 너무 많아 로지스틱적으로 실행할 수 없는 경우에는 가능한 조합 중 일부(보통 절반 이상)가 생략된 부분 요인 설계를 수행할 수 있습니다.
역사
요인 설계는 19세기에 로담스테드 실험 [1]스테이션의 John Bennet Lawes와 Joseph Henry Gilbert에 의해 사용되었다.
1926년에 Ronald Fisher는 요인 설계와 같은 "복잡한" 설계가 한 [2]번에 하나의 요인을 연구하는 것보다 더 효율적이라고 주장했습니다.피셔는 이렇게 말했다.
"현장 실험과 관련하여 더 자주 되풀이되는 격언은 없습니다. 네이처에게 몇 가지 질문을 해야 합니다. 이상적으로는 한 번에 한 가지 질문을 해야 합니다.작가는 이 견해가 완전히 틀렸다고 확신하고 있다.
그는 자연이 "논리적이고 신중하게 생각한 설문지"에 가장 잘 응답할 것이라고 제안한다.요인 설계를 사용하면 여러 요인의 효과와 요인 간의 교호작용을 동일한 정확도로 자체적으로 효과를 결정하는 데 필요한 횟수와 동일한 시행 횟수로 확인할 수 있습니다.
Frank Yates는 Yates 분석을 통해 특히 디자인 분석에 상당한 기여를 했습니다.
"팩토리얼"이라는 용어는 피셔가 그의 책 "실험의 [3]설계"에서 사용한 1935년 이전에는 인쇄물에 사용되지 않았을 수도 있습니다.
요인 실험의 이점
많은 사람들이 단일 요인 또는 변수의 효과만 조사합니다.이러한 단일 요인(OFAT) 실험과 비교하여 요인 실험은 여러 가지 이점을[4][5] 제공합니다.
- 요인 설계는 OFAT 실험보다 효율적입니다.이와 비슷하거나 더 낮은 비용으로 더 많은 정보를 제공합니다.그들은 OFAT 실험보다 더 빨리 최적의 조건을 찾을 수 있다.
- 요인 설계를 사용하면 추가 비용 없이 추가 요인을 조사할 수 있습니다.
- 한 요인의 효과가 다른 요인의 수준에 따라 다르면 OFAT 실험 설계에서는 탐지할 수 없습니다.이러한 교호작용을 탐지하려면 요인 설계가 필요합니다.교호작용이 있을 때 OFAT를 사용하면 요인에 따라 반응이 어떻게 변화하는지 심각하게 오해할 수 있습니다.
- 요인 설계를 사용하면 다른 요인의 여러 수준에서 요인의 효과를 추정할 수 있으므로 실험 조건의 범위에 걸쳐 유효한 결론을 얻을 수 있습니다.
요인 실험의 이점 예제
그의 저서 "거의 모든 것을 향상: 아이디어와 에세이, 통계학자 George Box는 요인 실험의 이점에 대한 많은 예를 제공합니다.여기 있습니다.[6]베어링 제조업체 SKF의 엔지니어들은 보다 저렴한 "케이지" 설계로 변경하는 것이 베어링 수명에 영향을 미치는지 확인하려고 했습니다.엔지니어들은 통계학자인 Christer Hellstrand에게 실험을 [7]설계하는 데 도움을 요청했다.
Box는 다음을 보고합니다."그 결과는 가속 수명 테스트를 통해 평가되었습니다.…실제 생산 라인에서 실행해야 하는 작업이었기 때문에 비용이 많이 들었습니다.실험자는 표준 케이지로 4회, 수정된 케이지로 4회 작업을 계획하고 있었습니다.Christer는 테스트하고 싶은 다른 요인이 있는지 물었습니다.그들은 있었지만 추가 운행은 예산을 초과하게 될 것이라고 말했다.Christer는 실행 횟수를 늘리지 않고 케이지 효과의 추정 정확도를 낮추지 않고 두 가지 요소를 "무료"로 테스트할 수 있는 방법을 보여 주었습니다.2×2×2 요인 설계라고 하는 이 배열에서는 세 가지 요인 각각이 두 가지 수준에서 실행되며 8가지 가능한 조합이 모두 포함된다.다양한 조합은 정육면체의 정점으로 편리하게 표시할 수 있습니다.두 경우 모두 표준조건은 마이너스 기호로, 수정조건은 플러스 기호로 표시됩니다.변경된 요인은 열처리, 외부 링 접촉 및 케이지 설계입니다.숫자는 베어링의 상대 수명을 나타냅니다.[입방체도]를 보면 케이지 설계를 선택해도 큰 차이가 없다는 것을 알 수 있습니다.그러나 케이지 설계의 숫자의 페어를 평균화하면 [아래 표]에 다른 두 가지 요소가 어떤 역할을 했는지 알 수 있습니다.… 이 특별한 응용 프로그램에서는 두 가지 요소(들)의 외륜 경합과 내륜 열처리를 함께 하면 베어링의 수명을 5배 늘릴 수 있다는 놀라운 사실을 발견했습니다."
| 조작 - | 조작 + | |
|---|---|---|
| 발열 - | 18 | 23 |
| 열 + | 21 | 106 |
"이러한 베어링이 수십 년 동안 만들어졌다는 것을 기억한다면, 이렇게 중요한 개선점을 발견하는 데 오랜 시간이 걸릴 수 있다는 것은 처음에는 놀라운 일입니다.대부분의 엔지니어가 최근까지 한 번에 하나의 요소만 사용했기 때문에 상호작용 효과가 누락되었다는 설명이 유력합니다."
예
가장 간단한 요인 실험에는 두 요인 각각에 대한 두 수준이 포함됩니다.한 엔지니어가 2000 RPM 또는 3000 RPM의 두 가지 다른 속도로 작동하는 두 개의 서로 다른 모터(A 및 B) 각각에 사용되는 총 전력을 연구하려고 합니다.요인 실험은 모터 A(2000RPM), 모터 B(2000RPM), 모터 A(3000RPM) 및 모터 B(3000RPM)의 네 가지 실험 단위로 구성됩니다.모든 요인에서 선택한 단일 수준의 각 조합은 한 번 표시됩니다.
이 실험은 2(또는 2×2) 요인2 실험의 예제이므로, 두 요인(검정력 또는 윗첨자) 각각에 대해 두 수준(기준값)을#factors 고려하므로 2=4 요인 점을 생성합니다2.
설계에는 많은 독립 변수가 포함될 수 있습니다.또한 입방체의 모서리로 표시된 8가지 실험 조건에서 세 가지 입력 변수의 효과를 평가할 수 있습니다.
이 작업은 의도된 목적과 사용 가능한 리소스에 따라 복제 유무에 관계없이 수행할 수 있습니다.종속 변수와 가능한 교호작용에 대한 세 가지 독립 변수의 효과를 제공합니다.
표기법
| A | B | |
|---|---|---|
| (1) | − | − |
| a | + | − |
| b | − | + |
| AB | + | + |
요인 실험을 나타내는 데 사용되는 표기법은 많은 정보를 전달합니다.설계가 2 요인임을3 나타내는 경우 이는 요인 수(3), 각 요인이 가지는 수준 수(2), 설계에 있는 실험 조건 수(2 = 8)를3 나타냅니다.마찬가지로, 2개의5 설계에는 각각 수준이 두 개인 5개의 요인이 있고5 2 = 32개의 실험 조건이 있습니다.요인 실험에는 수준 수가 다른 요인이 포함될 수 있습니다.23개 설계에는4 수준이 두 개인 4개, 수준이 세 개인 1개 등 5개의 요인이 있으며 16 × 3 = 48개의 실험 조건이 있습니다.[8]
공간을 절약하기 위해 2-수준 요인 실험의 점들은 종종 더하기 및 빼기 기호 문자열로 축약됩니다.문자열에는 요인만큼 많은 기호가 있으며, 각 요소의 레벨(통상은 첫 번째(또는 낮음) 레벨은 -{\ 두 번째(또는 높음) 레벨은+ {\을 나타냅니다.따라서 이 실험의 포인트는 - 및 로나타낼 수 있습니다.
또한 (1), a, b 및 ab로 축약할 수 있습니다. 여기서 문자가 있으면 지정된 요인이 높은 수준(또는 두 번째 수준)에 있고 문자가 없으면 지정된 요인이 낮은 수준(예: "a"는 요인 A가 높은 설정 상태에 있음을 나타냄)에 있음을 나타냅니다.는 낮은(또는 첫 번째) 설정입니다.(1)은 모든 요인이 가장 낮은(또는 처음) 값임을 나타내는 데 사용됩니다.
실행
두 개 이상의 요인의 경우 일반적으로kk−1 두 개의 요인 실험을k−1 반복실험하고 첫 번째 반복실험을 새 요인의 첫 번째(또는 낮은) 수준에 할당하고 두 번째 반복실험을 두 번째(또는 높은) 수준에 할당하여 두 번째 요인 실험을 재귀적으로 설계할 수 있습니다.이 프레임워크는 예를 들어 3가지 수준 요인에 대한 3가지 복제 설계 등으로 일반화할 수 있다.
요인 실험은 두 가지 방법으로 실험 오차를 추정할 수 있습니다.실험을 반복하거나 효과의 희박성 원리를 종종 이용할 수 있습니다.반복실험은 소규모 실험에서 더 일반적이며 실험 오류를 평가하는 매우 신뢰할 수 있는 방법입니다.요인의 수가 많은 경우(일반적으로 약 5개 이상이지만 응용 프로그램에 따라 다를 수 있음) 설계 복제가 어려울 수 있습니다.이 경우 설계의 단일 반복실험만 실행하고 특정 순서보다 큰 요인 교호작용(3개 이상의 요인 간)은 무시할 수 있다고 가정하는 것이 일반적입니다.이러한 가정 하에서 이러한 고차 교호작용의 추정치는 정확한 0에 대한 추정치이며, 따라서 실제로 실험 오차의 추정치입니다.
요인이 많으면 반복실험이 없어도 많은 실험 런이 필요합니다.예를 들어, 두 수준에서 각각 10개의 요인을 실험하면 2=120개의 조합이 생성됩니다10.비용이 많이 들거나 리소스가 부족하기 때문에 어느 시점에서는 이 작업이 불가능하게 됩니다.이 경우 부분 요인 설계를 사용할 수 있습니다.
다른 통계 실험과 마찬가지로 요인 실험의 실험 런은 치우침이 실험 결과에 미칠 수 있는 영향을 줄이기 위해 랜덤화해야 합니다.실제로는, 이것은 큰 운용상의 과제가 될 가능성이 있습니다.
요인 실험은 각 요인의 수준이 세 개 이상인 경우에 사용할 수 있습니다.그러나 3-수준(또는 그 이상) 요인 설계에 필요한 실험 런의 수는 2-수준 요인 설계의 경우보다 상당히 많습니다.따라서 연구자가 세 개 이상의 수준을 고려하려는 경우에는 요인 설계가 덜 매력적입니다.
분석.
요인 실험은 분산 분석 또는 회귀 [9]분석을 사용하여 분석할 수 있습니다.요인 "A"의 주효과를 계산하려면 A가 낮은(또는 첫 번째) 수준이었던 모든 실험 런의 평균 반응에서 A가 높은(또는 두 번째) 수준이었던 모든 실험 런의 평균 반응을 뺍니다.
요인 실험에 유용한 다른 탐색 분석 도구로는 주효과도, 교호작용도, Pareto 그림 및 추정된 효과의 정규 확률도가 있습니다.
요인이 연속형이면 2-수준 요인 설계는 효과가 선형이라고 가정합니다.요인에 대해 2차 효과가 기대되면 중심 합성 설계와 같이 더 복잡한 실험을 사용해야 합니다.2차 효과를 가질 수 있는 요인을 최적화하는 것이 반응 표면 방법론의 주요 목표입니다.
분석 예
Montgomery는 다음과 같은 요인 실험 분석 예를 제공합니다.
한 엔지니어가 화학 물질을 생산하는 공정의 여과율(출력)을 높이고 공정에 사용되는 포름알데히드의 양을 줄이려고 합니다.포름알데히드를 줄이려는 이전의 시도들은 여과율을 낮췄다.현재 여과율은 시간당 75갤런입니다.온도(A), 압력(B), 포름알데히드 농도(C), 교반 속도(D)의 4가지 요인을 고려한다.네 가지 요인 각각은 두 가지 수준에서 검정됩니다.
이후 마이너스(-) 기호와 플러스(+) 기호는 요인이 각각 낮은 수준에서 실행되는지 또는 높은 수준에서 실행되는지 나타냅니다.
| A | B | C | D | 여과율 |
|---|---|---|---|---|
| − | − | − | − | 45 |
| + | − | − | − | 71 |
| − | + | − | − | 48 |
| + | + | − | − | 65 |
| − | − | + | − | 68 |
| + | − | + | − | 60 |
| − | + | + | − | 80 |
| + | + | + | − | 65 |
| − | − | − | + | 43 |
| + | − | − | + | 100 |
| − | + | − | + | 45 |
| + | + | − | + | 104 |
| − | − | + | + | 75 |
| + | − | + | + | 86 |
| − | + | + | + | 70 |
| + | + | + | + | 96 |
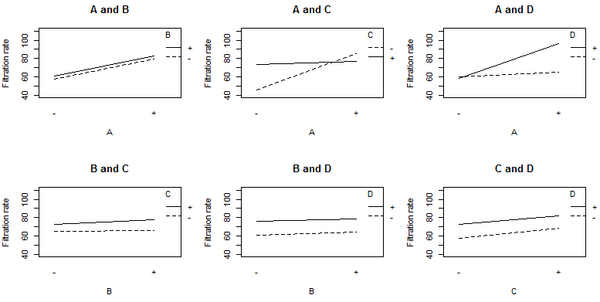
A:C 교호작용도의 평행하지 않은 선은 요인 A의 효과가 요인 C의 수준에 따라 달라진다는 것을 나타냅니다.A:D 교호작용에서도 유사한 결과가 유지됩니다.그래프를 보면 인자 B가 여과율에 거의 영향을 미치지 않습니다.네 가지 요인 및 요인 사이의 가능한 모든 교호작용 항을 포함하는 분산 분석(ANOVA)은 아래 표에 나와 있는 계수 추정치를 산출합니다.
| 계수 | 추정 |
|---|---|
| 가로채기 | 70.063 |
| A | 10.813 |
| B | 1.563 |
| C | 4.938 |
| D | 7.313 |
| A:B | 0.063 |
| A:C | −9.063 |
| B:C | 1.188 |
| A:D | 8.313 |
| B:D | −0.188 |
| C:D | −0.563 |
| A:B:C | 0.938 |
| A:B:D | 2.063 |
| A:C:D | −0.813 |
| B:C:D | −1.313 |
| A:B:C:D | 0.688 |
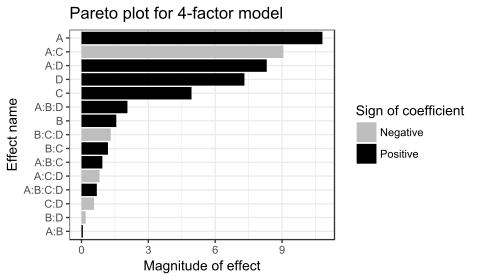
관측치가 16개이고 계수(절편, 주효과 및 교호작용)가 16개이므로 이 모형에 대해 p-값을 계산할 수 없습니다.계수 값과 그래프를 보면 중요한 요인이 A, C 및 D이고 교호작용 항 A:C와 A:D임을 알 수 있습니다.
A, C 및 D에 대한 계수는 분산 분석에서 모두 양수이므로 세 변수를 모두 높은 값으로 설정한 상태에서 공정을 실행하는 것이 좋습니다.그러나 각 변수의 주효과는 다른 변수의 수준에 대한 평균입니다.위의 A:C 교호작용도를 보면 요인 A의 효과가 요인 C의 수준에 따라 달라지며, 그 반대의 경우도 마찬가지입니다.인자 A(온도)는 인자 C가 + 수준일 때 여과율에 거의 영향을 미치지 않습니다.그러나 인자 A는 인자 C(포름알데히드)가 - 수준일 때 여과율에 큰 영향을 미친다.+ 레벨의 A와 - 레벨의 C를 조합하면 여과율이 가장 높아집니다.이 관측치는 단일 요인 분석이 어떻게 중요한 교호작용을 놓칠 수 있는지를 나타냅니다.엔지니어들은 요인 A와 C를 동시에 변화시켜야 요인 A의 효과가 요인 C의 수준에 따라 달라진다는 것을 알 수 있습니다.
최적의 여과율은 A와 D가 하이레벨, C가 로우레벨일 때 나타난다.이 결과는 또한 포름알데히드(인자 C)를 감소시키는 목적을 충족한다.B는 중요하지 않아 보이므로 모델에서 삭제할 수 있습니다.요인 A, C 및 D와 교호작용 항 A:C 및 A:D를 사용하여 분산 분석을 수행하면 모든 항이 유의한 다음 표(p-값 < 0.05)와 같은 결과를 얻을 수 있습니다.
| 계수 | 추정 | 표준오차 | t값 | p값 |
|---|---|---|---|---|
| 가로채기 | 70.062 | 1.104 | 63.444 | 2.3 × 10−14 |
| A | 10.812 | 1.104 | 9.791 | 1.9 × 10−6 |
| C | 4.938 | 1.104 | 4.471 | 1.2 × 10−3 |
| D | 7.313 | 1.104 | 6.622 | 5.9 × 10−5 |
| A:C | −9.063 | 1.104 | −8.206 | 9.4 × 10−6 |
| A:D | 8.312 | 1.104 | 7.527 | 2 × 10−5 |
「 」를 참조해 주세요.
메모들
- ^ Yates, Frank; Mather, Kenneth (1963). "Ronald Aylmer Fisher". Biographical Memoirs of Fellows of the Royal Society. London, England: Royal Society. 9: 91–120. doi:10.1098/rsbm.1963.0006. Archived from the original (PDF) on February 18, 2009.
- ^ Fisher, Ronald (1926). "The Arrangement of Field Experiments" (PDF). Journal of the Ministry of Agriculture of Great Britain. London, England: Ministry of Agriculture and Fisheries. 33: 503–513.
- ^ "Earliest Known Uses of Some of the Words of Mathematics (F)". jeff560.tripod.com.
- ^ a b Montgomery, Douglas C. (2013). Design and Analysis of Experiments (8th ed.). Hoboken, New Jersey: Wiley. ISBN 978-1119320937.
- ^ Oehlert, Gary (2000). A First Course in Design and Analysis of Experiments (Revised ed.). New York City: W. H. Freeman and Company. ISBN 978-0716735106.
- ^ George E.P., Box (2006). Improving Almost Anything: Ideas and Essays (Revised ed.). Hoboken, New Jersey: Wiley. ASIN B01FKSM9VY.
- ^ Hellstrand, C.; Oosterhoorn, A. D.; Sherwin, D. J.; Gerson, M. (24 February 1989). "The Necessity of Modern Quality Improvement and Some Experience with its Implementation in the Manufacture of Rolling Bearings [and Discussion]". Philosophical Transactions of the Royal Society. 327 (1596): 529–537. doi:10.1098/rsta.1989.0008.
- ^ Penn State University College of Health and Human Development (2011-12-22). "Introduction to Factorial Experimental Designs".
- ^ Cohen, J (1968). "Multiple regression as a general data-analytic system". Psychological Bulletin. 70 (6): 426–443. CiteSeerX 10.1.1.476.6180. doi:10.1037/h0026714.
레퍼런스
- Box, G. E.; Hunter, W. G.; Hunter, J. S. (2005). Statistics for Experimenters: Design, Innovation, and Discovery (2nd ed.). Wiley. ISBN 978-0-471-71813-0.



 나타냅니다.따라서 이 실험의 포인트는 -
나타냅니다.따라서 이 실험의 포인트는 -